
XXX . XXX Four-dimensional space
A four-dimensional space or 4D space is a mathematical extension of the concept of three-dimensional or 3D space. Three-dimensional space is the simplest possible generalization of the observation that one only needs three numbers, called dimensions, to describe the sizes or locations of objects in the everyday world. For example, the volume of a rectangular box is found by measuring its length (often labeled x), width (y), and depth (z).
The idea of adding a fourth dimension began with Joseph-Louis Lagrange in the mid-1700s and culminated in a precise formalization of the concept in 1854 by Bernhard Riemann. In 1880 Charles Howard Hinton popularized these insights in an essay titled What is the Fourth Dimension?, which explained the concept of a four-dimensional cube with a step-by-step generalization of the properties of lines, squares, and cubes. The simplest form of Hinton's method is to draw two ordinary cubes separated by an "unseen" distance, and then draw lines between their equivalent vertices. This can be seen in the accompanying animation, whenever it shows a smaller inner cube inside a larger outer cube. The eight lines connecting the vertices of the two cubes in that case represent a single direction in the "unseen" fourth dimension.
Higher dimensional spaces have since become one of the foundations for formally expressing modern mathematics and physics. Large parts of these topics could not exist in their current forms without the use of such spaces. Einstein's concept of spacetime uses such a 4D space, though it has a Minkowski structure that is a bit more complicated than Euclidean 4D space.
When dimensional locations are given as ordered lists of numbers such as (t,x,y,z) they are called vectors or n-tuples. It is only when such locations are linked together into more complicated shapes that the full richness and geometric complexity of 4D and higher spaces emerges. A hint of that complexity can be seen in the accompanying animation of one of simplest possible 4D objects, the 4D cube or tesseract.
The 4D equivalent of a cube, known as a tesseract. The tesseract is rotating in four dimensions, which are then projected into three dimensions.
Lagrange wrote in his Mécanique analytique (published 1788, based on work done around 1755) that mechanics can be viewed as operating in a four-dimensional space — three dimensions of space, and one of time.[1] In 1827 Möbius realized that a fourth dimension would allow a three-dimensional form to be rotated onto its mirror-image,[2]:141 and by 1853 Ludwig Schläfli had discovered many polytopes in higher dimensions, although his work was not published until after his death.[2]:142–143 Higher dimensions were soon put on firm footing by Bernhard Riemann's 1854 thesis, Über die Hypothesen welche der Geometrie zu Grunde liegen, in which he considered a "point" to be any sequence of coordinates (x1, ..., xn). The possibility of geometry in higher dimensions, including four dimensions in particular, was thus established.
An arithmetic of four dimensions called quaternions was defined by William Rowan Hamilton in 1843. This associative algebra was the source of the science of vector analysis in three dimensions as recounted in A History of Vector Analysis. Soon after tessarines and coquaternions were introduced as other four-dimensional algebras over R.
One of the first major expositors of the fourth dimension was Charles Howard Hinton, starting in 1880 with his essay What is the Fourth Dimension?; published in the Dublin University magazine.[3] He coined the terms tesseract, ana and kata in his book A New Era of Thought, and introduced a method for visualising the fourth dimension using cubes in the book Fourth Dimension.[4][5]
Hinton's ideas inspired a fantasy about a "Church of the Fourth Dimension" featured by Martin Gardner in his January 1962 "Mathematical Games column" in Scientific American. In 1886 Victor Schlegel described[6]his method of visualizing four-dimensional objects with Schlegel diagrams.
In 1908, Hermann Minkowski presented a paper[7] consolidating the role of time as the fourth dimension of spacetime, the basis for Einstein's theories of special and general relativity.[8] But the geometry of spacetime, being non-Euclidean, is profoundly different from that popularised by Hinton. The study of Minkowski space required new mathematics quite different from that of four-dimensional Euclidean space, and so developed along quite different lines. This separation was less clear in the popular imagination, with works of fiction and philosophy blurring the distinction, so in 1973 H. S. M. Coxeter felt compelled to write:
Vectors
Mathematically four-dimensional space is simply a space with four spatial dimensions, that is a space that needs four parameters to specify a point in it. For example, a general point might have position vector a, equal to
This can be written in terms of the four standard basis vectors (e1, e2, e3, e4), given by
so the general vector a is
Vectors add, subtract and scale as in three dimensions.
The dot product of Euclidean three-dimensional space generalizes to four dimensions as
and calculate or define the angle between two non-zero vectors as
Minkowski spacetime is four-dimensional space with geometry defined by a non-degenerate pairing different from the dot product:
As an example, the distance squared between the points (0,0,0,0) and (1,1,1,0) is 3 in both the Euclidean and Minkowskian 4-spaces, while the distance squared between (0,0,0,0) and (1,1,1,1) is 4 in Euclidean space and 2 in Minkowski space; increasing actually decreases the metric distance. This leads to many of the well-known apparent "paradoxes" of relativity.
The cross product is not defined in four dimensions. Instead the exterior product is used for some applications, and is defined as follows:
This is bivector valued, with bivectors in four dimensions forming a six-dimensional linear space with basis (e12, e13, e14, e23, e24, e34). They can be used to generate rotations in four dimensions.
Orthogonality and vocabulary
In the familiar three-dimensional space in which we live there are three coordinate axes—usually labeled x, y, and z—with each axis orthogonal (i.e. perpendicular) to the other two. The six cardinal directions in this space can be called up, down, east, west, north, and south. Positions along these axes can be called altitude, longitude, and latitude. Lengths measured along these axes can be called height, width, and depth.
Comparatively, four-dimensional space has an extra coordinate axis, orthogonal to the other three, which is usually labeled w. To describe the two additional cardinal directions, Charles Howard Hinton coined the terms ana and kata, from the Greek words meaning "up toward" and "down from", respectively. A position along the w axis can be called spissitude, as coined by Henry More.
Geometry
The geometry of four-dimensional space is much more complex than that of three-dimensional space, due to the extra degree of freedom.
Just as in three dimensions there are polyhedra made of two dimensional polygons, in four dimensions there are 4-polytopes made of polyhedra. In three dimensions, there are 5 regular polyhedra known as the Platonic solids. In four dimensions, there are 6 convex regular 4-polytopes, the analogues of the Platonic solids. Relaxing the conditions for regularity generates a further 58 convex uniform 4-polytopes, analogous to the 13 semi-regular Archimedean solids in three dimensions. Relaxing the conditions for convexity generates a further 10 nonconvex regular 4-polytopes.
| A4, [3,3,3] | B4, [4,3,3] | F4, [3,4,3] | H4, [5,3,3] | ||
|---|---|---|---|---|---|
 5-cell {3,3,3} |  tesseract {4,3,3} | 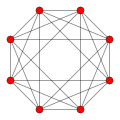 16-cell {3,3,4} |  24-cell {3,4,3} |  120-cell {5,3,3} |  600-cell {3,3,5} |
In three dimensions, a circle may be extruded to form a cylinder. In four dimensions, there are several different cylinder-like objects. A sphere may be extruded to obtain a spherical cylinder (a cylinder with spherical "caps", known as a spherinder), and a cylinder may be extruded to obtain a cylindrical prism (a cubinder). The Cartesian product of two circles may be taken to obtain a duocylinder. All three can "roll" in four-dimensional space, each with its own properties.
In three dimensions, curves can form knots but surfaces cannot (unless they are self-intersecting). In four dimensions, however, knots made using curves can be trivially untied by displacing them in the fourth direction—but 2D surfaces can form non-trivial, non-self-intersecting knots in 4D space.[9][page needed] Because these surfaces are two-dimensional, they can form much more complex knots than strings in 3D space can. The Klein bottle is an example of such a knotted surface.[citation needed] Another such surface is the real projective plane.
Hypersphere
The set of points in Euclidean 4-space having the same distance R from a fixed point P0 forms a hypersurface known as a 3-sphere. The hyper-volume of the enclosed space is:
This is part of the Friedmann–Lemaître–Robertson–Walker metric in General relativity where R is substituted by function R(t) with t meaning the cosmological age of the universe. Growing or shrinking R with time means expanding or collapsing universe, depending on the mass density inside.[10]
Cognition
Research using virtual reality finds that humans, in spite of living in a three-dimensional world, can, without special practice, make spatial judgments based on the length of, and angle between, line segments embedded in four-dimensional space.[11] The researchers noted that "the participants in our study had minimal practice in these tasks, and it remains an open question whether it is possible to obtain more sustainable, definitive, and richer 4D representations with increased perceptual experience in 4D virtual environments."[11] In another study,[12] the ability of humans to orient themselves in 2D, 3D and 4D mazes has been tested. Each maze consisted of four path segments of random length and connected with orthogonal random bends, but without branches or loops (i.e. actually labyrinths). The graphical interface was based on John McIntosh's free 4D Maze game.[13] The participating persons had to navigate through the path and finally estimate the linear direction back to the starting point. The researchers found that some of the participants were able to mentally integrate their path after some practice in 4D (the lower-dimensional cases were for comparison and for the participants to learn the method).
Dimensional analogy
To understand the nature of four-dimensional space, a device called dimensional analogy is commonly employed. Dimensional analogy is the study of how (n − 1) dimensions relate to n dimensions, and then inferring how n dimensions would relate to (n + 1) dimensions.
Dimensional analogy was used by Edwin Abbott Abbott in the book Flatland, which narrates a story about a square that lives in a two-dimensional world, like the surface of a piece of paper. From the perspective of this square, a three-dimensional being has seemingly god-like powers, such as ability to remove objects from a safe without breaking it open (by moving them across the third dimension), to see everything that from the two-dimensional perspective is enclosed behind walls, and to remain completely invisible by standing a few inches away in the third dimension.
By applying dimensional analogy, one can infer that a four-dimensional being would be capable of similar feats from our three-dimensional perspective. Rudy Rucker illustrates this in his novel Spaceland, in which the protagonist encounters four-dimensional beings who demonstrate such powers.
Cross-sections
As a three-dimensional object passes through a two-dimensional plane, a two-dimensional being would only see a cross-section of the three-dimensional object. For example, if a spherical balloon passed through a sheet of paper, a being on the paper would see first a single point, then a circle gradually growing larger, then smaller again until it shrank to a point and then disappeared. Similarly, if a four-dimensional object passed through three dimensions, we would see a three-dimensional cross-section of the four-dimensional object—for example, a hypersphere would appear first as a point, then as a growing sphere, with the sphere then shrinking to a single point and then disappearing.[15] This means of visualizing aspects of the fourth dimension was used in the novel Flatland and also in several works of Charles Howard Hinton.
Projections
A useful application of dimensional analogy in visualizing the fourth dimension is in projection. A projection is a way for representing an n-dimensional object in n − 1 dimensions. For instance, computer screens are two-dimensional, and all the photographs of three-dimensional people, places and things are represented in two dimensions by projecting the objects onto a flat surface. When this is done, depth is removed and replaced with indirect information. The retina of the eye is also a two-dimensional array of receptors but the brain is able to perceive the nature of three-dimensional objects by inference from indirect information (such as shading, foreshortening, binocular vision, etc.). Artists often use perspective to give an illusion of three-dimensional depth to two-dimensional pictures.
Similarly, objects in the fourth dimension can be mathematically projected to the familiar three dimensions, where they can be more conveniently examined. In this case, the 'retina' of the four-dimensional eye is a three-dimensional array of receptors. A hypothetical being with such an eye would perceive the nature of four-dimensional objects by inferring four-dimensional depth from indirect information in the three-dimensional images in its retina.
The perspective projection of three-dimensional objects into the retina of the eye introduces artifacts such as foreshortening, which the brain interprets as depth in the third dimension. In the same way, perspective projection from four dimensions produces similar foreshortening effects. By applying dimensional analogy, one may infer four-dimensional "depth" from these effects.
As an illustration of this principle, the following sequence of images compares various views of the three-dimensional cube with analogous projections of the four-dimensional tesseract into three-dimensional space.
| Cube | Tesseract | Description |
|---|---|---|
 |  | The image on the left is a cube viewed face-on. The analogous viewpoint of the tesseract in 4 dimensions is the cell-first perspective projection, shown on the right. One may draw an analogy between the two: just as the cube projects to a square, the tesseract projects to a cube.
Note that the other 5 faces of the cube are not seen here. They are obscured by the visible face. Similarly, the other 7 cells of the tesseract are not seen here because they are obscured by the visible cell.
|
 |  | The image on the left shows the same cube viewed edge-on. The analogous viewpoint of a tesseract is the face-first perspective projection, shown on the right. Just as the edge-first projection of the cube consists of two trapezoids, the face-first projection of the tesseract consists of two frustums.
The nearest edge of the cube in this viewpoint is the one lying between the red and green faces. Likewise, the nearest face of the tesseract is the one lying between the red and green cells.
|
 | 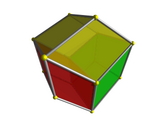 | On the left is the cube viewed corner-first. This is analogous to the edge-first perspective projection of the tesseract, shown on the right. Just as the cube's vertex-first projection consists of 3 deltoids surrounding a vertex, the tesseract's edge-first projection consists of 3 hexahedral volumes surrounding an edge. Just as the nearest vertex of the cube is the one where the three faces meet, so the nearest edge of the tesseract is the one in the center of the projection volume, where the three cells meet. |
 |  | A different analogy may be drawn between the edge-first projection of the tesseract and the edge-first projection of the cube. The cube's edge-first projection has two trapezoids surrounding an edge, while the tesseract has three hexahedral volumes surrounding an edge. |
 |  | On the left is the cube viewed corner-first. The vertex-first perspective projection of the tesseract is shown on the right. The cube's vertex-first projection has three tetragons surrounding a vertex, but the tesseract's vertex-first projection has four hexahedral volumes surrounding a vertex. Just as the nearest corner of the cube is the one lying at the center of the image, so the nearest vertex of the tesseract lies not on boundary of the projected volume, but at its center inside, where all four cells meet.
Note that only three faces of the cube's 6 faces can be seen here, because the other 3 lie behind these three faces, on the opposite side of the cube. Similarly, only 4 of the tesseract's 8 cells can be seen here; the remaining 4 lie behind these 4 in the fourth direction, on the far side of the tesseract.
|
Shadows
A concept closely related to projection is the casting of shadows.
If a light is shone on a three-dimensional object, a two-dimensional shadow is cast. By dimensional analogy, light shone on a two-dimensional object in a two-dimensional world would cast a one-dimensional shadow, and light on a one-dimensional object in a one-dimensional world would cast a zero-dimensional shadow, that is, a point of non-light. Going the other way, one may infer that light shone on a four-dimensional object in a four-dimensional world would cast a three-dimensional shadow.
If the wireframe of a cube is lit from above, the resulting shadow is a square within a square with the corresponding corners connected. Similarly, if the wireframe of a tesseract were lit from “above” (in the fourth dimension), its shadow would be that of a three-dimensional cube within another three-dimensional cube. (Note that, technically, the visual representation shown here is actually a two-dimensional image of the three-dimensional shadow of the four-dimensional wireframe figure.)
Bounding volumes
Dimensional analogy also helps in inferring basic properties of objects in higher dimensions. For example, two-dimensional objects are bounded by one-dimensional boundaries: a square is bounded by four edges. Three-dimensional objects are bounded by two-dimensional surfaces: a cube is bounded by 6 square faces. By applying dimensional analogy, one may infer that a four-dimensional cube, known as a tesseract, is bounded by three-dimensional volumes. And indeed, this is the case: mathematics shows that the tesseract is bounded by 8 cubes. Knowing this is key to understanding how to interpret a three-dimensional projection of the tesseract. The boundaries of the tesseract project to volumes in the image, not merely two-dimensional surfaces.
Visual scope
Being three-dimensional, we are only able to see the world with our eyes in two dimensions. A four-dimensional being would be able to see the world in three dimensions. For example, it would be able to see all six sides of an opaque box simultaneously, and in fact, what is inside the box at the same time, just as we can see the interior of a square on a piece of paper. It would be able to see all points in 3-dimensional space simultaneously, including the inner structure of solid objects and things obscured from our three-dimensional viewpoint. Our brains receive images in two dimensions and use reasoning to help us "picture" three-dimensional objects.
Limitations
Reasoning by analogy from familiar lower dimensions can be an excellent intuitive guide, but care must be exercised not to accept results that are not more rigorously tested. For example, consider the formulas for the circumference of a circle and the surface area of a sphere: . One might be tempted to suppose that the surface volume of a hypersphere is , or perhaps , but either of these would be wrong. The correct formula is .
exotic R4
In mathematics, an exotic R4 is a differentiable manifold that is homeomorphic but not diffeomorphic to the Euclidean space R4. The first examples were found in 1982 by Michael Freedman and others, by using the contrast between Freedman's theorems about topological 4-manifolds, and Simon Donaldson's theorems about smooth 4-manifolds. There is a continuum of non-diffeomorphic differentiable structures of R4, as was shown first by Clifford Taubes.
Prior to this construction, non-diffeomorphic smooth structures on spheres – exotic spheres – were already known to exist, although the question of the existence of such structures for the particular case of the 4-sphere remained open (and still remains open as of 2018). For any positive integer n other than 4, there are no exotic smooth structures on Rn; in other words, if n ≠ 4 then any smooth manifold homeomorphic to Rnis diffeomorphic to Rn.
Small exotic R4s
An exotic R4 is called small if it can be smoothly embedded as an open subset of the standard R4.
Small exotic R4s can be constructed by starting with a non-trivial smooth 5-dimensional h-cobordism (which exists by Donaldson's proof that the h-cobordism theorem fails in this dimension) and using Freedman's theorem that the topological h-cobordism theorem holds in this dimension.
Large exotic R4s
An exotic R4 is called large if it cannot be smoothly embedded as an open subset of the standard R4.
Examples of large exotic R4s can be constructed using the fact that compact 4-manifolds can often be split as a topological sum (by Freedman's work), but cannot be split as a smooth sum (by Donaldson's work).
Michael Hartley Freedman and Laurence R. Taylor (1986) showed that there is a maximal exotic R4, into which all other R4s can be smoothly embedded as open subsets.
Related exotic structures
Casson handles are homeomorphic to D2×R2 by Freedman's theorem (where D2 is the closed unit disc) but it follows from Donaldson's theorem that they are not all diffeomorphic to D2×R2. In other words, some Casson handles are exotic D2×R2s.
It is not known (as of 2017) whether or not there are any exotic 4-spheres; such an exotic 4-sphere would be a counterexample to the smooth generalized Poincaré conjecture in dimension 4. Some plausible candidates are given by Gluck twists.

example concept at : Transition maps
A transition map provides a way of comparing two charts of an atlas. To make this comparison, we consider the composition of one chart with the inverse of the other. This composition is not well-defined unless we restrict both charts to the intersection of their domains of definition. (For example, if we have a chart of Europe and a chart of Russia, then we can compare these two charts on their overlap, namely the European part of Russia.)
To be more precise, suppose that and are two charts for a manifold M such that is non-empty. The transition map is the map defined by
Note that since and are both homeomorphisms, the transition map is also a homeomorphism.
More structure
One often desires more structure on a manifold than simply the topological structure. For example, if one would like an unambiguous notion of differentiation of functions on a manifold, then it is necessary to construct an atlas whose transition functions are differentiable. Such a manifold is called differentiable. Given a differentiable manifold, one can unambiguously define the notion of tangent vectors and then directional derivatives.
If each transition function is a smooth map, then the atlas is called a smooth atlas, and the manifold itself is called smooth. Alternatively, one could require that the transition maps have only k continuous derivatives in which case the atlas is said to be .
Very generally, if each transition function belongs to a pseudo-group of homeomorphisms of Euclidean space, then the atlas is called a -atlas. If the transition maps between charts of an atlas preserve a local trivialization, then the atlas defines the structure of a fibre bundle.
XXX . XXX 4% zero 2 dimensional, 3 dimensional, 4 dimensional and 5 dimensional
for this question, first to understand what is dimension. dimension of a space is the number of mutually perpendicular straight lines that can be drawn in that space.
for example,
1) on a piece of paper, two such lines can be drawn so the page is 2 dimensional.
2)in/on a dice or box or room or something like that where 3 such lines can be drawn or imagined are 3 dimensional.
*a straight line itself is one dimensional (although there is some ambiguity if a curved line can be thought of as 1D considering a curved co-ordinate but that is different case in doing physics. in general, straight line is 1D).
*a point is said to be zero dimensional.
--these are about spatial dimensions. Now let's come to higher dimensions.
1) In pure mathematics, any number of dimensions can be assumed which has no need to be visualized. one has to generalize lower dimensional formulae using more than 3 variables.
2) In physics (specially in Special Relativity theory), time behaves like another dimension like spatial ones and including time, a 4D mathematical structure is used in relativistic mechanics which is called 'space-time' and the corresponding diagrammatic representation is called 'Minkowski space/diagram'. In General Relativity, mathematical analysis often uses previously discussed infinite dimensions but for practical cases, 4D is used for space-time.
for example,
1) on a piece of paper, two such lines can be drawn so the page is 2 dimensional.
2)in/on a dice or box or room or something like that where 3 such lines can be drawn or imagined are 3 dimensional.
*a straight line itself is one dimensional (although there is some ambiguity if a curved line can be thought of as 1D considering a curved co-ordinate but that is different case in doing physics. in general, straight line is 1D).
*a point is said to be zero dimensional.
--these are about spatial dimensions. Now let's come to higher dimensions.
1) In pure mathematics, any number of dimensions can be assumed which has no need to be visualized. one has to generalize lower dimensional formulae using more than 3 variables.
2) In physics (specially in Special Relativity theory), time behaves like another dimension like spatial ones and including time, a 4D mathematical structure is used in relativistic mechanics which is called 'space-time' and the corresponding diagrammatic representation is called 'Minkowski space/diagram'. In General Relativity, mathematical analysis often uses previously discussed infinite dimensions but for practical cases, 4D is used for space-time.
With each added dimension you gain an additional direction of reference.
A sheet of paper, for instance, is two dimensional. It has only length and width. Our human brains are hardwired to perceive three dimensions giving us one more direction of reference, height. After the three dimensions we can perceive, four or more dimensions become a challenge for the human mind to even imagine in terms of increasing directions of reference. Beyond doubt, at this point, we know additional dimensions surround us and have always been with us even though we are consciously unaware of them as a result of the way our brains function. Quantum, String Theory and M-Dimensional physics speaks of these additional dimensions as "enfolded" within in the three dimensions which frame our conscious awareness.
A sheet of paper, for instance, is two dimensional. It has only length and width. Our human brains are hardwired to perceive three dimensions giving us one more direction of reference, height. After the three dimensions we can perceive, four or more dimensions become a challenge for the human mind to even imagine in terms of increasing directions of reference. Beyond doubt, at this point, we know additional dimensions surround us and have always been with us even though we are consciously unaware of them as a result of the way our brains function. Quantum, String Theory and M-Dimensional physics speaks of these additional dimensions as "enfolded" within in the three dimensions which frame our conscious awareness.
Two dimensions
If you locate somebody by longitude and latitude on earth that is called two dimensional. Two dimensions can represent on paper very easily.
If you locate somebody by longitude and latitude on earth that is called two dimensional. Two dimensions can represent on paper very easily.
Three dimensions
When aircraft flying in air, its required minimum three dimensions to represent its position. These three dimensions are latitude, longitude and altitude. Three dimensions can't represent on paper or 2D computer screen.
When aircraft flying in air, its required minimum three dimensions to represent its position. These three dimensions are latitude, longitude and altitude. Three dimensions can't represent on paper or 2D computer screen.
Four dimensions
When aircraft flying in air its position can't represent easily by three dimensions. Because it's moving at every moment. So time is also required to explain when aircraft was available at particular position.
So now position represent by latitude, longitude, altitude and time.
When aircraft flying in air its position can't represent easily by three dimensions. Because it's moving at every moment. So time is also required to explain when aircraft was available at particular position.
So now position represent by latitude, longitude, altitude and time.
Imagine a one dimensional shape. It is is comprised of zero dimensional shapes (vertices).
A two dimensional shape is comprised of one dimensional shapes (sides) and zero dimensional shapes (vertices).
A three dimensional shape has two (faces), one (edges) and zero (faces) dimensional shapes that make it up.
So similarly, a four dimensional shape is like a three dimensional shape, but is also comprised of three dimensional shapes. This means that unlike being able to see the shape in two dimensions (like we do in our universe) we can see it in three dimensions. We could be able to see inside the shape, or around the shape.
This is all assuming, of course, that you are talking about spatial dimensions. We only live in one time dimension, meaning that our understanding of time is linear; we travel alone it, without being able to explore it. If you thought looking inside objects was mind-boggling, imagine living in a universe where you had free will on where in time to move!
A two dimensional shape is comprised of one dimensional shapes (sides) and zero dimensional shapes (vertices).
A three dimensional shape has two (faces), one (edges) and zero (faces) dimensional shapes that make it up.
So similarly, a four dimensional shape is like a three dimensional shape, but is also comprised of three dimensional shapes. This means that unlike being able to see the shape in two dimensions (like we do in our universe) we can see it in three dimensions. We could be able to see inside the shape, or around the shape.
This is all assuming, of course, that you are talking about spatial dimensions. We only live in one time dimension, meaning that our understanding of time is linear; we travel alone it, without being able to explore it. If you thought looking inside objects was mind-boggling, imagine living in a universe where you had free will on where in time to move!
in the sense of 4 dimensions is the changing and moving of space and time

The one dimensional interval


The TWO DIMENSIONAL SQUARE



THE THREE DIMENSIONAL CUBE



THE FOUR DIMENSIONAL CUBE : THE TESSERACT

STEREO VISION






A KNOTTY CHALLENGE





USING COLORS TO VISUALIZE THE EXTRA DIMENSIONS
XXX . XXX 4%zero null 0 Lumped element model jump to electronic circuit
The lumped element model (also called lumped parameter model, or lumped component model) simplifies the description of the behaviour of spatially distributed physical systems into a topology consisting of discrete entities that approximate the behaviour of the distributed system under certain assumptions. It is useful in electrical systems (including electronics), mechanical multibody systems, heat transfer, acoustics, etc.
Mathematically speaking, the simplification reduces the state space of the system to a finite dimension, and the partial differential equations (PDEs) of the continuous (infinite-dimensional) time and space model of the physical system into ordinary differential equations (ODEs) with a finite number of parameters.
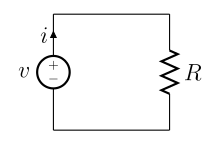
Electrical systems
Lumped matter discipline
The lumped matter discipline is a set of imposed assumptions in electrical engineering that provides the foundation for lumped circuit abstraction used in network analysis. The self-imposed constraints are:
1. The change of the magnetic flux in time outside a conductor is zero.
2. The change of the charge in time inside conducting elements is zero.
3. Signal timescales of interest are much larger than propagation delay of electromagnetic waves across the lumped element.
The first two assumptions result in Kirchhoff's circuit laws when applied to Maxwell's equations and are only applicable when the circuit is in steady state. The third assumption is the basis of the lumped element model used in network analysis. Less severe assumptions result in the distributed element model, while still not requiring the direct application of the full Maxwell equations.
Lumped element model
The lumped element model of electronic circuits makes the simplifying assumption that the attributes of the circuit, resistance, capacitance, inductance, and gain, are concentrated into idealized electrical components; resistors, capacitors, and inductors, etc. joined by a network of perfectly conducting wires.
The lumped element model is valid whenever , where denotes the circuit's characteristic length, and denotes the circuit's operating wavelength. Otherwise, when the circuit length is on the order of a wavelength, we must consider more general models, such as the distributed element model (including transmission lines), whose dynamic behaviour is described by Maxwell's equations. Another way of viewing the validity of the lumped element model is to note that this model ignores the finite time it takes signals to propagate around a circuit. Whenever this propagation time is not significant to the application the lumped element model can be used. This is the case when the propagation time is much less than the period of the signal involved. However, with increasing propagation time there will be an increasing error between the assumed and actual phase of the signal which in turn results in an error in the assumed amplitude of the signal. The exact point at which the lumped element model can no longer be used depends to a certain extent on how accurately the signal needs to be known in a given application.
Real-world components exhibit non-ideal characteristics which are, in reality, distributed elements but are often represented to a first-order approximation by lumped elements. To account for leakage in capacitors for example, we can model the non-ideal capacitor as having a large lumped resistor connected in parallel even though the leakage is, in reality distributed throughout the dielectric. Similarly a wire-wound resistor has significant inductance as well as resistance distributed along its length but we can model this as a lumped inductor in series with the ideal resistor.
Thermal systems
A lumped capacitance model, also called lumped system analysis, reduces a thermal system to a number of discrete “lumps” and assumes that the temperature difference inside each lump is negligible. This approximation is useful to simplify otherwise complex differential heat equations. It was developed as a mathematical analog of electrical capacitance, although it also includes thermal analogs of electrical resistance as well.
The lumped capacitance model is a common approximation in transient conduction, which may be used whenever heat conduction within an object is much faster than heat transfer across the boundary of the object. The method of approximation then suitably reduces one aspect of the transient conduction system (spatial temperature variation within the object) to a more mathematically tractable form (that is, it is assumed that the temperature within the object is completely uniform in space, although this spatially uniform temperature value changes over time). The rising uniform temperature within the object or part of a system, can then be treated like a capacitative reservoir which absorbs heat until it reaches a steady thermal state in time (after which temperature does not change within it).
An early-discovered example of a lumped-capacitance system which exhibits mathematically simple behavior due to such physical simplifications, are systems which conform to Newton's law of cooling. This law simply states that the temperature of a hot (or cold) object progresses toward the temperature of its environment in a simple exponential fashion. Objects follow this law strictly only if the rate of heat conduction within them is much larger than the heat flow into or out of them. In such cases it makes sense to talk of a single "object temperature" at any given time (since there is no spatial temperature variation within the object) and also the uniform temperatures within the object allow its total thermal energy excess or deficit to vary proportionally to its surface temperature, thus setting up the Newton's law of cooling requirement that the rate of temperature decrease is proportional to difference between the object and the environment. This in turn leads to simple exponential heating or cooling behavior (details below).
Method
To determine the number of lumps, the Biot number (Bi), a dimensionless parameter of the system, is used. Bi is defined as the ratio of the conductive heat resistance within the object to the convective heat transfer resistance across the object's boundary with a uniform bath of different temperature. When the thermal resistance to heat transferred into the object is larger than the resistance to heat being diffused completely within the object, the Biot number is less than 1. In this case, particularly for Biot numbers which are even smaller, the approximation of spatially uniform temperature within the object can begin to be used, since it can be presumed that heat transferred into the object has time to uniformly distribute itself, due to the lower resistance to doing so, as compared with the resistance to heat entering the object.
If the Biot number is less than 0.1 for a solid object, then the entire material will be nearly the same temperature with the dominant temperature difference will be at the surface. It may be regarded as being "thermally thin". The Biot number must generally be less than 0.1 for usefully accurate approximation and heat transfer analysis. The mathematical solution to the lumped system approximation gives Newton's law of cooling.
A Biot number greater than 0.1 (a "thermally thick" substance) indicates that one cannot make this assumption, and more complicated heat transfer equations for "transient heat conduction" will be required to describe the time-varying and non-spatially-uniform temperature field within the material body.
The single capacitance approach can be expanded to involve many resistive and capacitive elements, with Bi < 0.1 for each lump. As the Biot number is calculated based upon a characteristic length of the system, the system can often be broken into a sufficient number of sections, or lumps, so that the Biot number is acceptably small.
Some characteristic lengths of thermal systems are:
For arbitrary shapes, it may be useful to consider the characteristic length to be volume / surface area.
Thermal purely resistive circuits
A useful concept used in heat transfer applications once the condition of steady state heat conduction has been reached, is the representation of thermal transfer by what is known as thermal circuits. A thermal circuit is the representation of the resistance to heat flow in each element of a circuit, as though it were an electrical resistor. The heat transferred is analogous to the electric current and the thermal resistance is analogous to the electrical resistor. The values of the thermal resistance for the different modes of heat transfer are then calculated as the denominators of the developed equations. The thermal resistances of the different modes of heat transfer are used in analyzing combined modes of heat transfer. The lack of "capacitative" elements in the following purely resistive example, means that no section of the circuit is absorbing energy or changing in distribution of temperature. This is equivalent to demanding that a state of steady state heat conduction (or transfer, as in radiation) has already been established.
The equations describing the three heat transfer modes and their thermal resistances in steady state conditions, as discussed previously, are summarized in the table below:
| Transfer Mode | Rate of Heat Transfer | Thermal Resistance |
|---|---|---|
| Conduction | ||
| Convection | ||
| Radiation | , where |
In cases where there is heat transfer through different media (for example, through a composite material), the equivalent resistance is the sum of the resistances of the components that make up the composite. Likely, in cases where there are different heat transfer modes, the total resistance is the sum of the resistances of the different modes. Using the thermal circuit concept, the amount of heat transferred through any medium is the quotient of the temperature change and the total thermal resistance of the medium.
As an example, consider a composite wall of cross-sectional area . The composite is made of an long cement plaster with a thermal coefficient and long paper faced fiber glass, with thermal coefficient . The left surface of the wall is at and exposed to air with a convective coefficient of . The right surface of the wall is at and exposed to air with convective coefficient .
Using the thermal resistance concept, heat flow through the composite is as follows:
where
, , , and
Newton's law of cooling
Newton's law of cooling is an empirical relationship attributed to English physicist Sir Isaac Newton (1642 - 1727). This law stated in non-mathematical form is the following:
Or, using symbols:
An object at a different temperature from its surroundings will ultimately come to a common temperature with its surroundings. A relatively hot object cools as it warms its surroundings; a cool object is warmed by its surroundings. When considering how quickly (or slowly) something cools, we speak of its rate of cooling - how many degrees' change in temperature per unit of time.
The rate of cooling of an object depends on how much hotter the object is than its surroundings. The temperature change per minute of a hot apple pie will be more if the pie is put in a cold freezer than if it is placed on the kitchen table. When the pie cools in the freezer, the temperature difference between it and its surroundings is greater. On a cold day, a warm home will leak heat to the outside at a greater rate when there is a large difference between the inside and outside temperatures. Keeping the inside of a home at high temperature on a cold day is thus more costly than keeping it at a lower temperature. If the temperature difference is kept small, the rate of cooling will be correspondingly low.
As Newton's law of cooling states, the rate of cooling of an object - whether by conduction, convection, or radiation - is approximately proportional to the temperature difference ΔT. Frozen food will warm up faster in a warm room than in a cold room. Note that the rate of cooling experienced on a cold day can be increased by the added convection effect of the wind. This is referred to as wind chill. For example, a wind chill of -20 °C means that heat is being lost at the same rate as if the temperature were -20 °C without wind.
Applicable situations
This law describes many situations in which an object has a large thermal capacity and large conductivity, and is suddenly immersed in a uniform bath which conducts heat relatively poorly. It is an example of a thermal circuit with one resistive and one capacitative element. For the law to be correct, the temperatures at all points inside the body must be approximately the same at each time point, including the temperature at its surface. Thus, the temperature difference between the body and surroundings does not depend on which part of the body is chosen, since all parts of the body have effectively the same temperature. In these situations, the material of the body does not act to "insulate" other parts of the body from heat flow, and all of the significant insulation (or "thermal resistance") controlling the rate of heat flow in the situation resides in the area of contact between the body and its surroundings. Across this boundary, the temperature-value jumps in a discontinuous fashion.
In such situations, heat can be transferred from the exterior to the interior of a body, across the insulating boundary, by convection, conduction, or diffusion, so long as the boundary serves as a relatively poor conductor with regard to the object's interior. The presence of a physical insulator is not required, so long as the process which serves to pass heat across the boundary is "slow" in comparison to the conductive transfer of heat inside the body (or inside the region of interest—the "lump" described above).
In such a situation, the object acts as the "capacitative" circuit element, and the resistance of the thermal contact at the boundary acts as the (single) thermal resistor. In electrical circuits, such a combination would charge or discharge toward the input voltage, according to a simple exponential law in time. In the thermal circuit, this configuration results in the same behavior in temperature: an exponential approach of the object temperature to the bath temperature.
Mathematical statement
Newton's law is mathematically stated by the simple first-order differential equation:
where
- Q is thermal energy in joules
- h is the heat transfer coefficient between the surface and the fluid
- A is the surface area of the heat being transferred
- T is the temperature of the object's surface and interior (since these are the same in this approximation)
- Tenv is the temperature of the environment
- ΔT(t) = T(t) - Tenv is the time-dependent thermal gradient between environment and object
Putting heat transfers into this form is sometimes not a very good approximation, depending on ratios of heat conductances in the system. If the differences are not large, an accurate formulation of heat transfers in the system may require analysis of heat flow based on the (transient) heat transfer equation in nonhomogeneous or poorly conductive media.
Solution in terms of object heat capacity
If the entire body is treated as lumped capacitance heat reservoir, with total heat content which is proportional to simple total heat capacity , and , the temperature of the body, or . It is expected that the system will experience exponential decay with time in the temperature of a body.
From the definition of heat capacity comes the relation . Differentiating this equation with regard to time gives the identity (valid so long as temperatures in the object are uniform at any given time): . This expression may be used to replace in the first equation which begins this section, above. Then, if is the temperature of such a body at time , and is the temperature of the environment around the body:
where
is a positive constant characteristic of the system, which must be in units of , and is therefore sometimes expressed in terms of a characteristic time constant given by: . Thus, in thermal systems, . (The total heat capacity of a system may be further represented by its mass-specific heat capacity multiplied by its mass , so that the time constant is also given by ).
The solution of this differential equation, by standard methods of integration and substitution of boundary conditions, gives:
If:
- is defined as : where is the initial temperature difference at time 0,
then the Newtonian solution is written as:
This same solution is almost immediately apparent if the initial differential equation is written in terms of , as the single function to be solved for. '
Applications
This mode of analysis has been applied to forensic sciences to analyze the time of death of humans. Also, it can be applied to HVAC (heating, ventilating and air-conditioning, which can be referred to as "building climate control"), to ensure more nearly instantaneous effects of a change in comfort level setting.[3]
Mechanical systems
The simplifying assumptions in this domain are:
- all objects are rigid bodies;
- all interactions between rigid bodies take place via kinematic pairs (joints), springs and dampers.
Acoustics
In this context, the lumped component model extends the distributed concepts of Acoustic theory subject to approximation. In the acoustical lumped component model, certain physical components with acoustical properties may be approximated as behaving similarly to standard electronic components or simple combinations of components.
- A rigid-walled cavity containing air (or similar compressible fluid) may be approximated as a capacitor whose value is proportional to the volume of the cavity. The validity of this approximation relies on the shortest wavelength of interest being significantly (much) larger than the longest dimension of the cavity.
- A reflex port may be approximated as an inductor whose value is proportional to the effective length of the port divided by its cross-sectional area. The effective length is the actual length plus an end correction. This approximation relies on the shortest wavelength of interest being significantly larger than the longest dimension of the port.
- Certain types of damping material can be approximated as a resistor. The value depends on the properties and dimensions of the material. The approximation relies in the wavelengths being long enough and on the properties of the material itself.
- A loudspeaker drive unit (typically a woofer or subwoofer drive unit) may be approximated as a series connection of a zero-impedance voltage source, a resistor, a capacitor and an inductor. The values depend on the specifications of the unit and the wavelength of interest.
Heat transfer for buildings
The simplifying assumption in this domain are:
- all heat transfer mechanisms are linear, implying that radiation and convection are linearised for each problem;
Several publications can be found that describe how to generate LEMs of buildings. In most cases, the building is considered a single thermal zone and in this case, turning multi-layered walls into Lumped Elements can be one of the most complicated tasks in the creation of the model. Ramallo-González's method (Dominant Layer Method) is the most accurate and simple so far.[4] In this method, one of the layers is selected as the dominant layer in the whole construction, this layer is chosen considering the most relevant frequencies of the problem. In his thesis, Ramallo-González shows the whole process of obtaining the LEM of a complete building.
LEMs of buildings have also been used to evaluate the efficiency of domestic energy systems In this case the LEMs allowed to run many simulations under different future weather scenarios.
XXX . XXX 4%zero null 0 1 2 Isomorphism
In mathematics, an isomorphism (from the Ancient Greek: ἴσος isos "equal", and μορφή morphe "form" or "shape") is a homomorphism or morphism (i.e. a mathematical mapping) that admits an inverse.[note 1] Two mathematical objects are isomorphic if an isomorphism exists between them. An automorphism is an isomorphism whose source and target coincide. The interest of isomorphisms lies in the fact that two isomorphic objects cannot be distinguished by using only the properties used to define morphisms; thus isomorphic objects may be considered the same as long as one considers only these properties and their consequences.
For most algebraic structures, including groups and rings, a homomorphism is an isomorphism if and only if it is bijective.
In topology, where the morphisms are continuous functions, isomorphisms are also called homeomorphisms or bicontinuous functions. In mathematical analysis, where the morphisms are differentiable functions, isomorphisms are also called diffeomorphisms.
A canonical isomorphism is a canonical map that is an isomorphism. Two objects are said to be canonically isomorphic if there is a canonical isomorphism between them. For example, the canonical map from a finite-dimensional vector space V to its second dual space is a canonical isomorphism; on the other hand, V is isomorphic to its dual space but not canonically in general.
Isomorphisms are formalized using category theory. A morphism f : X → Y in a category is an isomorphism if it admits a two-sided inverse, meaning that there is another morphism g : Y → X in that category such that gf = 1X and fg = 1Y, where 1X and 1Y are the identity morphisms of X and Y, respectively.

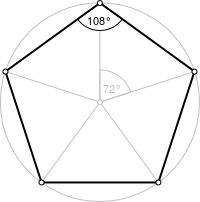
The group of fifth roots of unity under multiplication is isomorphic to the group of rotations of the regular pentagon under composition.
Examples
Logarithm and exponential
Let be the multiplicative group of positive real numbers, and let be the additive group of real numbers.
The logarithm function satisfies for all , so it is a group homomorphism. The exponential function satisfies for all , so it too is a homomorphism.
The identities and show that and are inverses of each other. Since is a homomorphism that has an inverse that is also a homomorphism, is an isomorphism of groups.
Because is an isomorphism, it translates multiplication of positive real numbers into addition of real numbers. This facility makes it possible to multiply real numbers using a ruler and a table of logarithms, or using a slide rule with a logarithmic scale.
Integers modulo 6
Consider the group , the integers from 0 to 5 with addition modulo 6. Also consider the group , the ordered pairs where the x coordinates can be 0 or 1, and the y coordinates can be 0, 1, or 2, where addition in the x-coordinate is modulo 2 and addition in the y-coordinate is modulo 3.
These structures are isomorphic under addition, under the following scheme:
- (0,0) ↦ 0
- (1,1) ↦ 1
- (0,2) ↦ 2
- (1,0) ↦ 3
- (0,1) ↦ 4
- (1,2) ↦ 5
or in general (a,b) ↦ (3a + 4b) mod 6.
For example, (1,1) + (1,0) = (0,1), which translates in the other system as 1 + 3 = 4.
Even though these two groups "look" different in that the sets contain different elements, they are indeed isomorphic: their structures are exactly the same. More generally, the direct product of two cyclic groups and is isomorphic to if and only if m and n are coprime, per the Chinese remainder theorem.
Relation-preserving isomorphism
If one object consists of a set X with a binary relation R and the other object consists of a set Y with a binary relation S then an isomorphism from X to Y is a bijective function ƒ: X → Y such that:[2]
S is reflexive, irreflexive, symmetric, antisymmetric, asymmetric, transitive, total, trichotomous, a partial order, total order, strict weak order, total preorder (weak order), an equivalence relation, or a relation with any other special properties, if and only if R is.
For example, R is an ordering ≤ and S an ordering , then an isomorphism from X to Y is a bijective function ƒ: X → Y such that
Such an isomorphism is called an order isomorphism or (less commonly) an isotone isomorphism.
If X = Y, then this is a relation-preserving automorphism.
Isomorphism vs. bijective morphism
In a concrete category (that is, roughly speaking, a category whose objects are sets and morphisms are mappings between sets), such as the category of topological spaces or categories of algebraic objects like groups, rings, and modules, an isomorphism must be bijective on the underlying sets. In algebraic categories (specifically, categories of varieties in the sense of universal algebra), an isomorphism is the same as a homomorphism which is bijective on underlying sets. However, there are concrete categories in which bijective morphisms are not necessarily isomorphisms (such as the category of topological spaces), and there are categories in which each object admits an underlying set but in which isomorphisms need not be bijective (such as the homotopy category of CW-complexes).
Applications
In abstract algebra, two basic isomorphisms are defined:
- Group isomorphism, an isomorphism between groups
- Ring isomorphism, an isomorphism between rings. (Isomorphisms between fields are actually ring isomorphisms)
Just as the automorphisms of an algebraic structure form a group, the isomorphisms between two algebras sharing a common structure form a heap. Letting a particular isomorphism identify the two structures turns this heap into a group.
In mathematical analysis, the Laplace transform is an isomorphism mapping hard differential equations into easier algebraic equations.
In category theory, let the category C consist of two classes, one of objects and the other of morphisms. Then a general definition of isomorphism that covers the previous and many other cases is: an isomorphism is a morphism ƒ: a → b that has an inverse, i.e. there exists a morphism g: b → a with ƒg = 1b and gƒ = 1a. For example, a bijective linear map is an isomorphism between vector spaces, and a bijective continuous function whose inverse is also continuous is an isomorphism between topological spaces, called a homeomorphism.
In graph theory, an isomorphism between two graphs G and H is a bijective map f from the vertices of G to the vertices of H that preserves the "edge structure" in the sense that there is an edge from vertex u to vertex v in G if and only if there is an edge from ƒ(u) to ƒ(v) in H. See graph isomorphism.
In mathematical analysis, an isomorphism between two Hilbert spaces is a bijection preserving addition, scalar multiplication, and inner product.
In early theories of logical atomism, the formal relationship between facts and true propositions was theorized by Bertrand Russell and Ludwig Wittgenstein to be isomorphic. An example of this line of thinking can be found in Russell's Introduction to Mathematical Philosophy.
In cybernetics, the good regulator or Conant–Ashby theorem is stated "Every good regulator of a system must be a model of that system". Whether regulated or self-regulating, an isomorphism is required between the regulator and processing parts of the system.
Relation with equality
In certain areas of mathematics, notably category theory, it is valuable to distinguish between equality on the one hand and isomorphism on the other.[3] Equality is when two objects are exactly the same, and everything that's true about one object is true about the other, while an isomorphism implies everything that's true about a designated part of one object's structure is true about the other's. For example, the sets
- and
are equal; they are merely different presentations—the first an intensional one (in set builder notation), and the second extensional (by explicit enumeration)—of the same subset of the integers. By contrast, the sets {A,B,C} and {1,2,3} are not equal—the first has elements that are letters, while the second has elements that are numbers. These are isomorphic as sets, since finite sets are determined up to isomorphism by their cardinality (number of elements) and these both have three elements, but there are many choices of isomorphism—one isomorphism is
- while another is
and no one isomorphism is intrinsically better than any other.[note 2][note 3] On this view and in this sense, these two sets are not equal because one cannot consider them identical: one can choose an isomorphism between them, but that is a weaker claim than identity—and valid only in the context of the chosen isomorphism.
Sometimes the isomorphisms can seem obvious and compelling, but are still not equalities. As a simple example, the genealogical relationships among Joe, John, and Bobby Kennedy are, in a real sense, the same as those among the American football quarterbacks in the Manning family: Archie, Peyton, and Eli. The father-son pairings and the elder-brother-younger-brother pairings correspond perfectly. That similarity between the two family structures illustrates the origin of the word isomorphism (Greek iso-, "same," and -morph, "form" or "shape"). But because the Kennedys are not the same people as the Mannings, the two genealogical structures are merely isomorphic and not equal.
Another example is more formal and more directly illustrates the motivation for distinguishing equality from isomorphism: the distinction between a finite-dimensional vector space V and its dual spaceV* = { φ: V → K} of linear maps from V to its field of scalars K. These spaces have the same dimension, and thus are isomorphic as abstract vector spaces (since algebraically, vector spaces are classified by dimension, just as sets are classified by cardinality), but there is no "natural" choice of isomorphism . If one chooses a basis for V, then this yields an isomorphism: For all u. v ∈ V,
- .
This corresponds to transforming a column vector (element of V) to a row vector (element of V*) by transpose, but a different choice of basis gives a different isomorphism: the isomorphism "depends on the choice of basis". More subtly, there is a map from a vector space V to its double dual V** = { x: V* → K} that does not depend on the choice of basis: For all v ∈ V and φ ∈ V*,
- .
This leads to a third notion, that of a natural isomorphism: while V and V** are different sets, there is a "natural" choice of isomorphism between them. This intuitive notion of "an isomorphism that does not depend on an arbitrary choice" is formalized in the notion of a natural transformation; briefly, that one may consistently identify, or more generally map from, a vector space to its double dual, , for any vector space in a consistent way. Formalizing this intuition is a motivation for the development of category theory.
However, there is a case where the distinction between natural isomorphism and equality is usually not made. That is for the objects that may be characterized by a universal property. In fact, there is a unique isomorphism, necessarily natural, between two objects sharing the same universal property. A typical example is the set of real numbers, which may be defined through infinite decimal expansion, infinite binary expansion, Cauchy sequences, Dedekind cuts and many other ways. Formally these constructions define different objects, which all are solutions of the same universal property. As these objects have exactly the same properties, one may forget the method of construction and considering them as equal. This is what everybody does when talking of "the set of the real numbers". The same occurs with quotient spaces: they are commonly constructed as sets of equivalence classes. However, talking of set of sets may be counterintuitive, and quotient spaces are commonly considered as a pair of a set of undetermined objects, often called "points", and a surjective map onto this set.
If one wishes to draw a distinction between an arbitrary isomorphism (one that depends on a choice) and a natural isomorphism (one that can be done consistently), one may write ≈ for an unnatural isomorphism and ≅ for a natural isomorphism, as in V ≈ V* and V ≅ V**. This convention is not universally followed, and authors who wish to distinguish between unnatural isomorphisms and natural isomorphisms will generally explicitly state the distinction.
Generally, saying that two objects are equal is reserved for when there is a notion of a larger (ambient) space that these objects live in. Most often, one speaks of equality of two subsets of a given set (as in the integer set example above), but not of two objects abstractly presented. For example, the 2-dimensional unit sphere in 3-dimensional space
- and the Riemann sphere
which can be presented as the one-point compactification of the complex plane C ∪ {∞} or as the complex projective line (a quotient space)
are three different descriptions for a mathematical object, all of which are isomorphic, but not equal because they are not all subsets of a single space: the first is a subset of R3, the second is C ≅ R2[note 4] plus an additional point, and the third is a subquotient of C2
In the context of category theory, objects are usually at most isomorphic—indeed, a motivation for the development of category theory was showing that different constructions in homology theory yielded equivalent (isomorphic) groups. Given maps between two objects X and Y, however, one asks if they are equal or not (they are both elements of the set Hom(X, Y), hence equality is the proper relationship), particularly in commutative diagrams.
Notes
- ^ For clarity, by inverse is meant inverse homomorphism or inverse morphism respectively, not inverse function.
- ^ A, B, C have a conventional order, namely alphabetical order, and similarly 1, 2, 3 have the order from the integers, and thus one particular isomorphism is "natural", namely
- .
- ^ In fact, there are precisely different isomorphisms between two sets with three elements. This is equal to the number of automorphisms of a given three-element set (which in turn is equal to the order of the symmetric group on three letters), and more generally one has that the set of isomorphisms between two objects, denoted is a torsor for the automorphism group of A, and also a torsor for the automorphism group of B. In fact, automorphisms of an object are a key reason to be concerned with the distinction between isomorphism and equality, as demonstrated in the effect of change of basis on the identification of a vector space with its dual or with its double dual, as elaborated in the sequel.
- ^ Being precise, the identification of the complex numbers with the real plane,
XXX . XXX 4%zero null 0 1 2 3 4 Equation of time
The equation of time describes the discrepancy between two kinds of solar time. The word equation is used in the medieval sense of "reconcile a difference". The two times that differ are the apparent solar time, which directly tracks the diurnal motion of the Sun, and mean solar time, which tracks a theoretical mean Sun with noons 24 hours apart. Apparent solar time can be obtained by measurement of the current position (hour angle) of the Sun, as indicated (with limited accuracy) by a sundial. Mean solar time, for the same place, would be the time indicated by a steady clock set so that over the year its differences from apparent solar time would resolve to zero.
The equation of time is the east or west component of the analemma, a curve representing the angular offset of the Sun from its mean position on the celestial sphere as viewed from Earth. The equation of time values for each day of the year, compiled by astronomical observatories, were widely listed in almanacs and ephemerides .
The concept
During a year the equation of time varies as shown on the graph; its change from one year to the next is slight. Apparent time, and the sundial, can be ahead (fast) by as much as 16 min 33 s (around 3 November), or behind (slow) by as much as 14 min 6 s (around 12 February). The equation of time has zeros near 15 April, 13 June, 1 September and 25 December. Ignoring very slow changes in the Earth's orbit and rotation, these events are repeated at the same times every tropical year. However, due to the non-integer number of days in a year, these dates can vary by a day or so from year to year.
The graph of the equation of time is closely approximated by the sum of two sine curves, one with a period of a year and one with a period of half a year. The curves reflect two astronomical effects, each causing a different non-uniformity in the apparent daily motion of the Sun relative to the stars:
- the obliquity of the ecliptic (the plane of the Earth's annual orbital motion around the Sun), which is inclined by about 23.44 degrees relative to the plane of the Earth's equator; and
- the eccentricity of the Earth's orbit around the Sun, which is about 0.0167.
The equation of time is constant only for a planet with zero axial tilt and zero orbital eccentricity. On Mars the difference between sundial time and clock time can be as much as 50 minutes, due to the considerably greater eccentricity of its orbit. The planet Uranus, which has an extremely large axial tilt, has an equation of time that makes its days start and finish several hours earlier or later depending on where it is in its orbit.
Sign of the equation of time
There is no universally accepted definition of the sign of the equation of time. Some publications show it as positive when a sundial is ahead of a clock, as shown in the upper graph above; others when the clock is ahead of the sundial, as shown in the lower graph. In the English-speaking world, the former usage is the more common, but is not always followed. Anyone who makes use of a published table or graph should first check its sign usage. Often, there is a note or caption which explains it. Otherwise, the sign can be determined by knowing that, during the first three months of each year, the clock is ahead of the sundial. The mnemonic "NYSS" (pronounced "nice"), for "new year, sundial slow", can be useful. Some published tables avoid the ambiguity by not using signs, but by showing phrases such as "sundial fast" or "sundial slow" instead.[6]
In this article, and others in English Wikipedia, a positive value of the equation of time implies that a sundial is ahead of a clock.

Flash Back
The phrase "equation of time" is derived from the medieval Latin, aequātiō diērum meaning "equation of days" or "difference of days". The word aequātiō was widely used in early astronomy to tabulate the difference between an observed value and the expected value (as in the equation of centre, the equation of the equinoxes, the equation of the epicycle). The difference between apparent solar time and mean time was recognized by astronomers since antiquity, but prior to the invention of accurate mechanical clocks in the mid-17th century, sundials were the only reliable timepieces, and apparent solar time was the generally accepted standard.
A description of apparent and mean time was given by Nevil Maskelyne in the Nautical Almanac for 1767: "Apparent Time is that deduced immediately from the Sun, whether from the Observation of his passing the Meridian, or from his observed Rising or Setting. This Time is different from that shewn by Clocks and Watches well regulated at Land, which is called equated or mean Time." He went on to say that, at sea, the apparent time found from observation of the Sun must be corrected by the equation of time, if the observer requires the mean time.[1]
The right time was originally considered to be that which was shown by a sundial. When good mechanical clocks were introduced, they agreed with sundials only near four dates each year, so the equation of time was used to "correct" their readings to obtain sundial time. Some clocks, called equation clocks, included an internal mechanism to perform this "correction". Later, as clocks became the dominant good timepieces, uncorrected clock time, i.e., "mean time" became the accepted standard. The readings of sundials, when they were used, were then, and often still are, corrected with the equation of time, used in the reverse direction from previously, to obtain clock time. Many sundials, therefore, have tables or graphs of the equation of time engraved on them to allow the user to make this correction.
The equation of time was used historically to set clocks. Between the invention of accurate clocks in 1656 and the advent of commercial time distribution services around 1900, there were three common land-based ways to set clocks. Firstly, in the unusual event of having an astronomer present, the sun's transit across the meridian (the moment the sun passed overhead) was noted, the clock was then set to noon and offset by the number of minutes given by the equation of time for that date. Secondly, and much more commonly, a sundial was read, a table of the equation of time (usually engraved on the dial) was consulted and the watch or clock set accordingly. These calculated the mean time, albeit local to a point of longitude. (The third method did not use the equation of time; instead, it used stellar observations to give sidereal time, exploiting the relationship between sidereal time and mean solar time.)[7]
Of course, the equation of time can still be used, when required, to obtain apparent solar time from clock time. Devices such as solar trackers, which move to keep pace with the Sun's movements in the sky, frequently do not include sensors to determine the Sun's position. Instead, they are controlled by a clock mechanism, along with a mechanism that incorporates the equation of time to make the device keep pace with the Sun.
Ancient history — Babylon and Egypt
The irregular daily movement of the Sun was known by the Babylonians. Book III of Ptolemy's Almagest is primarily concerned with the Sun's anomaly, and he tabulated the equation of time in his Handy Tables.[8]Ptolemy discusses the correction needed to convert the meridian crossing of the Sun to mean solar time and takes into consideration the nonuniform motion of the Sun along the ecliptic and the meridian correction for the Sun's ecliptic longitude. He states the maximum correction is 81⁄3 time-degrees or 5⁄9 of an hour (Book III, chapter 9).[9] However he did not consider the effect to be relevant for most calculations since it was negligible for the slow-moving luminaries and only applied it for the fastest-moving luminary, the Moon.
Medieval and Renaissance astronomy
Based on Ptolemy's discussion in the Almagest, medieval Islamic astronomers such as al-Khwarizmi, al-Battani, Kushyar ibn Labban, Jamshīd al-Kāshī and others, made improvements to the solar tables and the value of obliquity, and published tables of the equation of time (taʿdīl al-ayyām bi layālayhā) in their zij (astronomical tables).[10]
After that, the next substantial improvement in the computation didn't come until Kepler's final upset of the geocentric astronomy of the ancients. Gerald J. Toomer uses the medieval term "equation" from the Latin aequātiō[n 1], for Ptolemy's difference between the mean solar time and the apparent solar time. Johannes Kepler's definition of the equation is "the difference between the number of degrees and minutes of the mean anomaly and the degrees and minutes of the corrected anomaly."[11]
Apparent time versus mean time
Until the invention of the pendulum and the development of reliable clocks during the 17th century, the equation of time as defined by Ptolemy remained a curiosity, of importance only to astronomers. However, when mechanical clocks started to take over timekeeping from sundials, which had served humanity for centuries, the difference between clock time and sundial time became an issue for everyday life. Apparent solar time is the time indicated by the Sun on a sundial (or measured by its transit over a preferred local meridian), while mean solar time is the average as indicated by well-regulated clocks. The first tables to give the equation of time in an essentially correct way were published in 1665 by Christiaan Huygens.[12] Huygens, following the tradition of Ptolemy and medieval astronomers in general, set his values for the equation of time so as to make all values positive throughout the year.[13][n 2]
Another set of tables was published in 1672–73 by John Flamsteed, who later became the first Astronomer Royal of the new Royal Greenwich Observatory. These appear to have been the first essentially correct tables that gave today's meaning of Mean Time (rather than mean time based on the latest sunrise of the year as proposed by Huygens). Flamsteed adopted the convention of tabulating and naming the correction in the sense that it was to be applied to the apparent time to give mean time.[14]
The equation of time, correctly based on the two major components of the Sun's irregularity of apparent motion,[n 3] was not generally adopted until after Flamsteed's tables of 1672–73, published with the posthumous edition of the works of Jeremiah Horrocks.[15]
Robert Hooke (1635–1703), who mathematically analyzed the universal joint, was the first to note that the geometry and mathematical description of the (non-secular) equation of time and the universal joint were identical, and proposed the use of a universal joint in the construction of a "mechanical sundial".
18th and early 19th centuries
The corrections in Flamsteed's tables of 1672–1673 and 1680 gave mean time computed essentially correctly and without need for further offset. But the numerical values in tables of the equation of time have somewhat changed since then, owing to three factors:
- general improvements in accuracy that came from refinements in astronomical measurement techniques,
- slow intrinsic changes in the equation of time, occurring as a result of small long-term changes in the Earth's obliquity and eccentricity (affecting, for instance, the distance and dates of perihelion), and
- the inclusion of small sources of additional variation in the apparent motion of the Sun, unknown in the 17th century, but discovered from the 18th century onwards, including the effects of the Moon[n 4], Venus and Jupiter.[17]
From 1767 to 1833, the British Nautical Almanac and Astronomical Ephemeris tabulated the equation of time in the sense 'mean minus apparent solar time'. Times in the Almanac were in apparent solar time, because time aboard ship was most often determined by observing the Sun. In the unusual case that the mean solar time of an observation was needed, one would apply the equation of time to apparent solar time. In the issues since 1834, all times have been in mean solar time, because by then the time aboard ship was increasingly often determined by marine chronometers. In the unusual case that the apparent solar time of an observation was needed, one would apply the equation of time to mean solar time, requiring all differences in the equation of time to have the opposite sign than before.
As the apparent daily movement of the Sun is one revolution per day, that is 360° every 24 hours, and the Sun itself appears as a disc of about 0.5° in the sky, simple sundials can be read to a maximum accuracy of about one minute. Since the equation of time has a range of about 33 minutes, the difference between sundial time and clock time cannot be ignored. In addition to the equation of time, one also has to apply corrections due to one's distance from the local time zone meridian and summer time, if any.
The tiny increase of the mean solar day due to the slowing down of the Earth's rotation, by about 2 ms per day per century, which currently accumulates up to about 1 second every year, is not taken into account in traditional definitions of the equation of time, as it is imperceptible at the accuracy level of sundials.
Major components of the equation
 Eccentricity of the Earth's orbit
Eccentricity of the Earth's orbit
The Earth revolves around the Sun. As seen from Earth, the Sun appears to revolve once around the Earth through the background stars in one year. If the Earth orbited the Sun with a constant speed, in a circular orbit in a plane perpendicular to the Earth's axis, then the Sun would culminate every day at exactly the same time, and be a perfect time keeper (except for the very small effect of the slowing rotation of the Earth). But the orbit of the Earth is an ellipse not centered on the Sun, and its speed varies between 30.287 and 29.291 km/s, according to Kepler's laws of planetary motion, and its angular speed also varies, and thus the Sun appears to move faster (relative to the background stars) at perihelion (currently around 3 January) and slower at aphelion a half year later. [18][not in citation given]
At these extreme points this effect varies the apparent solar day by 7.9 s/day from its mean. Consequently, the smaller daily differences on other days in speed are cumulative until these points, reflecting how the planet accelerates and decelerates compared to the mean. As a result, the eccentricity of the Earth's orbit contributes a periodic variation which is (in the first-order approximation) a sine wave with an amplitude of 7.66 min and a period of one year to the equation of time. The zero points are reached at perihelion (at the beginning of January) and aphelion (beginning of July); the extreme values are in early April (negative) and early October (positive).
Obliquity of the ecliptic
However, even if the Earth's orbit were circular, the perceived motion of the Sun along our celestial equator would still not be uniform. This is a consequence of the tilt of the Earth's rotational axis with respect to the plane of its orbit, or equivalently, the tilt of the ecliptic (the path Sun appears to take in the celestial sphere) with respect to the celestial equator. The projection of this motion onto our celestial equator, along which "clock time" is measured, is a maximum at the solstices, when the yearly movement of the Sun is parallel to the equator (causing amplification of perceived speed) and yields mainly a change in right ascension. It is a minimum at the equinoxes, when the Sun's apparent motion is more sloped and yields more change in declination, leaving less for the component in right ascension, which is the only component that affects the duration of the solar day. A practical illustration of obliquity is that the daily shift of the shadow cast by the Sun in a sundial even on the equator is smaller close to the equinoxes and greater close to the solstices. If this effect operated alone, then days would be up to 24 hours and 20.3 seconds long (measured solar noon to solar noon) near the solstices, and as much as 20.3 seconds shorter than 24 hours near the equinoxes.[19][not in citation given]
In the figure on the right, we can see the monthly variation of the apparent slope of the plane of the ecliptic at solar midday as seen from Earth. This variation is due to the apparent precession of the rotating Earth through the year, as seen from the Sun at solar midday.
In terms of the equation of time, the inclination of the ecliptic results in the contribution of a sine wave variation with an amplitude of 9.87 minutes and a period of a half year to the equation of time. The zero points of this sine wave are reached at the equinoxes and solstices, while the extrema are at the beginning of February and August (negative) and the beginning of May and November (positive).
Secular effects
The two above mentioned factors have different wavelengths, amplitudes and phases, so their combined contribution is an irregular wave. At epoch 2000 these are the values (in minutes and seconds with UT dates):
| Point | Value | Date |
|---|---|---|
| minimum | −14 min 15 s | 11 February |
| zero | 0 min 0 s | 15 April |
| maximum | +3 min 41 s | 14 May |
| zero | 0 min 0 s | 13 June |
| minimum | −6 min 30 s | 26 July |
| zero | 0 min 0 s | 1 September |
| maximum | +16 min 25 s | 3 November |
| zero | 0 min 0 s | 25 December |
- E.T. = apparent − mean. Positive means: Sun runs fast and culminates earlier, or the sundial is ahead of mean time. A slight yearly variation occurs due to presence of leap years, resetting itself every 4 years.
The exact shape of the equation of time curve and the associated analemma slowly change[20] over the centuries, due to secular variations in both eccentricity and obliquity. At this moment both are slowly decreasing, but they increase and decrease over a timescale of hundreds of thousands of years. If and when the Earth's orbital eccentricity (now about 0.0167 and slowly decreasing) reaches 0.047, the eccentricity effect may in some circumstances overshadow the obliquity effect, leaving the equation of time curve with only one maximum and minimum per year, as is the case on Mars.
On shorter timescales (thousands of years) the shifts in the dates of equinox and perihelion will be more important. The former is caused by precession, and shifts the equinox backwards compared to the stars. But it can be ignored in the current discussion as our Gregorian calendar is constructed in such a way as to keep the vernal equinox date at 21 March (at least at sufficient accuracy for our aim here). The shift of the perihelion is forwards, about 1.7 days every century. In 1246 the perihelion occurred on 22 December, the day of the solstice, so the two contributing waves had common zero points and the equation of time curve was symmetrical: in Astronomical Algorithms Meeus gives February and November extrema of 15 m 39 s and May and July ones of 4 m 58 s. Before then the February minimum was larger than the November maximum, and the May maximum larger than the July minimum. In fact, in years before −1900 (1901 BCE) the May maximum was larger than the November maximum. In the year −2000 (2001 BCE) the May maximum was +12 minutes and a couple seconds while the November maximum was just less than 10 minutes. The secular change is evident when one compares a current graph of the equation of time (see below) with one from 2000 years ago, e.g., one constructed from the data of Ptolemy.
Graphical representation
Practical use
If the gnomon (the shadow-casting object) is not an edge but a point (e.g., a hole in a plate), the shadow (or spot of light) will trace out a curve during the course of a day. If the shadow is cast on a plane surface, this curve will be a conic section (usually a hyperbola), since the circle of the Sun's motion together with the gnomon point define a cone. At the spring and fall equinoxes, the cone degenerates into a plane and the hyperbola into a line. With a different hyperbola for each day, hour marks can be put on each hyperbola which include any necessary corrections. Unfortunately, each hyperbola corresponds to two different days, one in each half of the year, and these two days will require different corrections. A convenient compromise is to draw the line for the "mean time" and add a curve showing the exact position of the shadow points at noon during the course of the year. This curve will take the form of a figure eight and is known as an analemma. By comparing the analemma to the mean noon line, the amount of correction to be applied generally on that day can be determined.
The equation of time is used not only in connection with sundials and similar devices, but also for many applications of solar energy. Machines such as solar trackers and heliostats have to move in ways that are influenced by the equation of time.
Civil time is the local mean time for a meridian that often passes near the center of the time zone, and may possibly be further altered by daylight saving time. When the apparent solar time that corresponds to a given civil time is to be found, the difference in longitude between the site of interest and the time zone meridian, daylight saving time, and the equation of time must all be considered.
Calculating the equation of time
The equation of time is obtained from a published table, or a graph. For dates in the past such tables are produced from historical measurements, or by calculation; for future dates, of course, tables can only be calculated. In devices such as computer-controlled heliostats the computer is often programmed to calculate the equation of time. The calculation can be numerical or analytical. The former are based on numerical integration of the differential equations of motion, including all significant gravitational and relativistic effects. The results are accurate to better than 1 second and are the basis for modern almanac data. The latter are based on a solution that includes only the gravitational interaction between the Sun and Earth, simpler than but not as accurate as the former. Its accuracy can be improved by including small corrections.
The following discussion describes a reasonably accurate (agreeing with Almanac data to within 3 seconds over a wide range of years) algorithm for the equation of time that is well known to astronomers.[23] It also shows how to obtain a simple approximate formula (accurate to within 1 minute over a large time interval), that can be easily evaluated with a calculator and provides the simple explanation of the phenomenon that was used previously in this article.
Mathematical description
The precise definition of the equation of time is
- EOT = GHA − GMHA
The quantities occurring in this equation are
- EOT, the time difference between apparent solar time and mean solar time;
- GHA, the Greenwich Hour Angle of the apparent (actual) Sun;
- GMHA = Universal Time − Offset, the Greenwich Mean Hour Angle of the mean (fictitious) Sun.
Here time and angle are quantities that are related by factors such as: 2π radians = 360° = 1 day = 24 hours. The difference, EOT, is measurable since GHA is an angle that can be measured and Universal Time, UT, is a scale for the measurement of time. The offset by π = 180° = 12 hours from UT is needed because UT is zero at mean midnight while GMHA = 0 at mean noon.[n 5] Both GHA and GMHA, like all physical angles, have a mathematical, but not a physical discontinuity at their respective (apparent and mean) noon. Despite the mathematical discontinuities of its components, EOT is defined as a continuous function by adding (or subtracting) 24 hours in the small time interval between the discontinuities in GHA and GMHA.
According to the definitions of the angles on the celestial sphere GHA = GAST − α (see hour angle)
where:
where:
- GAST is the Greenwich apparent sidereal time (the angle between the apparent vernal equinox and the meridian in the plane of the equator). This is a known function of UT.[25]
- α is the right ascension of the apparent Sun (the angle between the apparent vernal equinox and the actual Sun in the plane of the equator).
On substituting into the equation of time, it is
- EOT = GAST − α − UT + offset
Like the formula for GHA above, one can write GMHA = GAST − αM, where the last term is the right ascension of the mean Sun. The equation is often written in these terms as[26]
- EOT = αM − α
where αM = GAST − UT + offset. In this formulation a measurement or calculation of EOT at a certain value of time depends on a measurement or calculation of α at that time. Both α and αM vary from 0 to 24 hours during the course of a year. The former has a discontinuity at a time that depends on the value of UT, while the later has its at a slightly later time. As a consequence, when calculated this way EOT has two, artificial, discontinuities. They can both be removed by subtracting 24 hours from the value of EOT in the small time interval after the discontinuity in α and before the one in αM. The resulting EOT is a continuous function of time.
Another definition, denoted E to distinguish it from EOT, is
- E = GMST − α − UT + offset
Here GMST = GAST − eqeq, is the Greenwich mean sidereal time (the angle between the mean vernal equinox and the mean Sun in the plane of the equator). Therefore, GMST is an approximation to GAST (and Eis an approximation to EOT); eqeq is called the equation of the equinoxes and is due to the wobbling, or nutation of the Earth's axis of rotation about its precessional motion. Since the amplitude of the nutational motion is only about 1.2 s (18″ of longitude) the difference between EOT and E can be ignored unless one is interested in subsecond accuracy.
A third definition, denoted Δt to distinguish it from EOT and E, and now called the Equation of Ephemeris Time[27] (prior to the distinction that is now made between EOT, E, and Δt the latter was known as the equation of time) is
- Δt = Λ − α
here Λ is the ecliptic longitude of the mean Sun (the angle from the mean vernal equinox to the mean Sun in the plane of the ecliptic).
The difference Λ − (GMST − UT + offset) is 1.3 s from 1960 to 2040. Therefore, over this restricted range of years Δt is an approximation to EOT whose error is in the range 0.1 to 2.5 s depending on the longitude correction in the equation of the equinoxes; for many purposes, for example correcting a sundial, this accuracy is more than good enough.
Right ascension calculation
The right ascension, and hence the equation of time, can be calculated from Newton's two-body theory of celestial motion, in which the bodies (Earth and Sun) describe elliptical orbits about their common mass center. Using this theory, the equation of time becomes
- Δt = M + λp − α
where the new angles that appear are
- M = 2π(t − tp)tY, is the mean anomaly, the angle from the periapsis of the elliptical orbit to the mean Sun; its range is from 0 to 2π as t increases from tp to tp + tY;
- tY = 365.2596358 days is the length of time in an anomalistic year: the time interval between two successive passages of the periapsis;
- λp = Λ − M, is the ecliptic longitude of the periapsis;
- t is dynamical time, the independent variable in the theory. Here it is taken to be identical with the continuous time based on UT (see above), but in more precise calculations (of E or EOT) the small difference between them must be accounted for[28] as well as the distinction between UT1 and UTC.
To complete the calculation three additional angles are required:
- E, the Sun's eccentric anomaly (note that this is different from M);
- ν, the Sun's true anomaly;
- λ = ν + λp, the Sun's true longitude on the ecliptic.
All these angles are shown in the figure on the right, which shows the celestial sphere and the Sun's elliptical orbit seen from the Earth (the same as the Earth's orbit seen from the Sun). In this figure ε is the obliquity, while e = √1 − (b/a)2 is the eccentricity of the ellipse.
Now given a value of 0 ≤ M ≤ 2π, one can calculate α(M) by means of the following well-known procedure:[23]
- M = E − e sin E
Although this equation cannot be solved exactly in closed form, values of E(M) can be obtained from infinite (power or trigonometric) series, graphical, or numerical methods. Alternatively, note that for e = 0, E = M, and by iteration:[30]
- E ≈ M + e sin M.
This approximation can be improved, for small e, by iterating again,
- E ≈ M + e sin M + 12e2 sin 2M,
and continued iteration produces successively higher order terms of the power series expansion in e. For small values of e (much less than 1) two or three terms of the series give a good approximation for E; the smaller e, the better the approximation.
The correct branch of the multiple valued function tan−1 x to use is the one that makes ν a continuous function of E(M) starting from νE=0 = 0. Thus for 0 ≤ E < π use tan−1 x = Tan−1 x, and for π < E ≤ 2π use tan−1 x = Tan−1 x + π. At the specific value E = π for which the argument of tan is infinite, use ν = E. Here Tan−1 x is the principal branch, |Tan−1 x| < π2; the function that is returned by calculators and computer applications. Alternatively, this function can be expressed in terms of its Taylor series in e, the first three terms of which are:
- ν ≈ E + e sin E + 14e2 sin 2E.
For small e this approximation (or even just the first two terms) is a good one. Combining the approximation for E(M) with this one for ν(E) produces
- ν ≈ M + 2e sin M + 54e2 sin 2M.
The relation ν(M) is called the equation of the center; the expression written here is a second-order approximation in e. For the small value of e that characterises the Earth's orbit this gives a very good approximation for ν(M).
Next, knowing ν, calculate λ from its definition:
- λ = ν + λp
The value of λ varies non-linearly with M because the orbit is elliptical and not circular. From the approximation for ν:
- λ ≈ M + λp + 2e sin M + 54e2 sin 2M.
Finally, knowing λ calculate α from a relation for the right triangle on the celestial sphere shown above
- α = tan−1(cos ε tan λ)
Note that the quadrant of α is the same as that of λ, therefore reduce λ to the range 0 to 2π and write
- α = Tan−1 (cos ε tan λ) + kπ,
where k is 0 if λ is in quadrant 1, it is 1 if λ is in quadrants 2 or 3 and it is 2 if λ is in quadrant 4. For the values at which tan is infinite, α = λ.
Although approximate values for α can be obtained from truncated Taylor series like those for ν,[33] it is more efficacious to use the equation[34]
- α = λ − sin−1 [y sin (α + λ)]
where y = tan2(ε2). Note that for ε = y = 0, α = λ and iterating twice:
- α ≈ λ − y sin 2λ + 12y2 sin 4λ.
Equation of time
The equation of time is obtained by substituting the result of the right ascension calculation into an equation of time formula. Here Δt(M) = M + λp − α[λ(M)] is used; in part because small corrections (of the order of 1 second), that would justify using E, are not included, and in part because the goal is to obtain a simple analytical expression. Using two term approximations for λ(M) and α(λ), allows Δt to be written as an explicit expression of two terms, which is designated Δtey because it is a first order approximation in e and in y.
- Δtey = −2e sin M + y sin (2M + 2λp) = −7.659 sin M + 9.863 sin (2M + 3.5932) minutes
This equation was first derived by Milne,[35] who wrote it in terms of λ = M + λp. The numerical values written here result from using the orbital parameter values, e = 0.016709, ε = 23.4393° = 0.409093 radians, and λp = 282.9381° = 4.938201 radians that correspond to the epoch 1 January 2000 at 12 noon UT1. When evaluating the numerical expression for Δtey as given above, a calculator must be in radian mode to obtain correct values because the value of 2λp − 2π in the argument of the second term is written there in radians. Higher order approximations can also be written,[36] but they necessarily have more terms. For example, the second order approximation in both e and y consists of five terms[37]
- Δte2y2 = Δtey − 54e2 sin 2M + ey sin M cos (2M + 2λp) − 12y2 sin (4M + 4λp)
This approximation has the potential for high accuracy, however, in order to achieve it over a wide range of years, the parameters e, ε, and λp must be allowed to vary with time.[38] This creates additional calculational complications. Other approximations have been proposed, for example, Δte[39] which uses the first order equation of the center but no other approximation to determine α, and Δte2[40] which uses the second order equation of the center.
The time variable, M, can be written either in terms of n, the number of days past perihelion, or D, the number of days past a specific date and time (epoch):
- M = 2πtYn days = MD + 2πtYD days = 6.24004077 + 0.01720197D
Here MD is the value of M at the chosen date and time. For the values given here, in radians, MD is that measured for the actual Sun at the epoch, 1 January 2000 at 12 noon UT1, and D is the number of days past that epoch. At periapsis M = 2π, so solving gives D = Dp = 2.508109. This puts the periapsis on 4 January 2000 at 00:11:41 while the actual periapsis is, according to results from the Multiyear Interactive Computer Almanac[41] (abbreviated as MICA), on 3 January 2000 at 05:17:30. This large discrepancy happens because the difference between the orbital radius at the two locations is only 1 part in a million; in other words, radius is a very weak function of time near periapsis. As a practical matter this means that one cannot get a highly accurate result for the equation of time by using n and adding the actual periapsis date for a given year. However, high accuracy can be achieved by using the formulation in terms of D.
When D > Dp, M is greater than 2π and one must subtract a multiple of 2π (that depends on the year) from it to bring it into the range 0 to 2π. Likewise for years prior to 2000 one must add multiples of 2π. For example, for the year 2010, D varies from 3653 on 1 January at noon to 4017 on 31 December at noon, the corresponding M values are 69.0789468 and 75.3404748 and are reduced to the range 0 to 2π by subtracting 10 and 11 times 2π respectively. One can always write D = nY + d, where nY is the number of days from the epoch to noon on 1 January of the desired year, and 0 ≤ d ≤ 364 (365 if the calculation is for a leap year).
The result of the computations is usually given as either a set of tabular values, or a graph of the equation of time as a function of d. A comparison of plots of Δt, Δtey, and results from MICA all for the year 2000 is shown in the figure on the right. The plot of Δteyis seen to be close to the results produced by MICA, the absolute error, Err = |Δtey − MICA2000|, is less than 1 minute throughout the year; its largest value is 43.2 seconds and occurs on day 276 (3 October). The plot of Δt is indistinguishable from the results of MICA, the largest absolute error between the two is 2.46 s on day 324 (20 November).
Remark on the continuity of the equation of time
For the choice of the appropriate branch of the arctan relation with respect to function continuity a modified version of the arctangent function is helpful. It brings in previous knowledge about the expected value by a parameter. The modified arctangent function is defined as:
- arctanη x = arctan x + π round (η − arctan xπ).
It produces a value that is as close to η as possible. The function round rounds to the nearest integer.
Applying this yields:
- Δt(M) = M + λp − arctan(M+λp) (cos ε tan λ).
The parameter M + λp arranges here to set Δt to the zero nearest value which is the desired one.
Secular effects
The difference between the MICA and Δt results was checked every 5 years over the range from 1960 to 2040. In every instance the maximum absolute error was less than 3 s; the largest difference, 2.91 s, occurred on 22 May 1965 (day 141). However, in order to achieve this level of accuracy over this range of years it is necessary to account for the secular change in the orbital parameters with time. The equations that describe this variation are:[42]
According to these relations, in 100 years (D = 36525), λp increases by about 0.5% (1.7°), e decreases by about 0.25%, and ε decreases by about 0.05%.
As a result, the number of calculations required for any of the higher-order approximations of the equation of time requires a computer to complete them, if one wants to achieve their inherent accuracy over a wide range of time. In this event it is no more difficult to evaluate Δt using a computer than any of its approximations.
In all this note that Δtey as written above is easy to evaluate, even with a calculator, is accurate enough (better than 1 minute over the 80-year range) for correcting sundials, and has the nice physical explanation as the sum of two terms, one due to obliquity and the other to eccentricity that was used previously in the article. This is not true either for Δt considered as a function of M or for any of its higher-order approximations.
Alternative calculation
Another calculation of the equation of time can be done as follows.] Angles are in degrees; the conventional order of operations applies.
- W = 360°365.24 days
W is the Earth's mean angular orbital velocity in degrees per day.
- A = W × (D + 10)
D is the date, in days starting at zero on 1 January (i.e. the days part of the ordinal date minus 1). 10 is the approximate number of days from the December solstice to 1 January. A is the angle the earth would move on its orbit at its average speed from the December solstice to date D.
- B = A + 360°π × 0.0167 × sin [W(D − 2)]
B is the angle the Earth moves from the solstice to date D, including a first-order correction for the Earth's orbital eccentricity, 0.0167. The number 2 is the number of days from 1 January to the date of the Earth's perihelion. This expression for B can be simplified by combining constants to:
- B = A + 1.914° × sin [W(D − 2)].
C is the difference between the angles moved at mean speed, and at the corrected speed projected onto the equatorial plane, and divided by 180 to get the difference in "half turns". The value 23.44° is the obliquity (tilt) of the Earth's axis. The subtraction gives the conventional sign to the equation of time. For any given value of x, arctan x (sometimes written as tan−1 x) has multiple values, differing from each other by integer numbers of half turns. The value generated by a calculator or computer may not be the appropriate one for this calculation. This may cause C to be wrong by an integer number of half turns. The excess half turns are removed in the next step of the calculation to give the equation of time:
- EOT = 720 × (C − nint(C)) minutes
The expression nint(C) means the nearest integer to C. On a computer, it can be programmed, for example, as INT(C + 0.5). It is 0, 1, or 2 at different times of the year. Subtracting it leaves a small positive or negative fractional number of half turns, which is multiplied by 720, the number of minutes (12 hours) that the Earth takes to rotate one half turn relative to the Sun, to get the equation of time.
Compared with published values,[6] this calculation has a root mean square error of only 3.7 s. The greatest error is 6.0 s. This is much more accurate than the approximation described above, but not as accurate as the elaborate calculation.
Addendum about solar declination
The value of B in the above calculation is an accurate value for the Sun's ecliptic longitude (shifted by 90°), so the solar declination becomes readily available:
- Declination = −arcsin (sin 23.44° × cos B)
which is accurate to within a fraction of a degree.
XXX . XXX 4%zero null 0 1 2 3 4 5 6 grow atomically thin transistors and circuits
In an advance that helps pave the way for next-generation electronics and computing technologies—and possibly paper-thin gadgets —scientists with the U.S. Department of Energy's Lawrence Berkeley National Laboratory (Berkeley Lab) developed a way to chemically assemble transistors and circuits that are only a few atoms thick.
What's more, their method yields functional structures at a scale large enough to begin thinking about real-world applications and commercial scalability.
The scientists controlled the synthesis of a transistor in which narrow channels were etched onto conducting graphene, and a semiconducting material called a transition-metal dichalcogenide, or TMDC, was seeded in the blank channels. Both of these materials are single-layered crystals and atomically thin, so the two-part assembly yielded electronic structures that are essentially two-dimensional. In addition, the synthesis is able to cover an area a few centimeters long and a few millimeters wide.
"This is a big step toward a scalable and repeatable way to build atomically thin electronics or pack more computing power in a smaller area,
Their work is part of a new wave of research aimed at keeping pace with Moore's Law, which holds that the number of transistors in an integrated circuit doubles approximately every two years. In order to keep this pace, scientists predict that integrated electronics will soon require transistors that measure less than ten nanometers in length.
Transistors are electronic switches, so they need to be able to turn on and off, which is a characteristic of semiconductors. However, at the nanometer scale, silicon transistors likely won't be a good option. That's because silicon is a bulk material, and as electronics made from silicon become smaller and smaller, their performance as switches dramatically decreases, which is a major roadblock for future electronics.
Researchers have looked to two-dimensional crystals that are only one molecule thick as alternative materials to keep up with Moore's Law. These crystals aren't subject to the constraints of silicon.
In this vein, the Berkeley Lab scientists developed a way to seed a single-layered semiconductor, in this case the TMDC molybdenum disulfide (MoS2), into channels lithographically etched within a sheet of conducting graphene. The two atomic sheets meet to form nanometer-scale junctions that enable graphene to efficiently inject current into the MoS2. These junctions make atomically thin transistors.
"This approach allows for the chemical assembly of electronic circuits, using two-dimensional materials, which show improved performance compared to using traditional metals to inject current into TMDCs," says Mervin Zhao, a lead author and Ph.D. student in Zhang's group at Berkeley Lab and UC Berkeley.
Optical and electron microscopy images, and spectroscopic mapping, confirmed various aspects related to the successful formation and functionality of the two-dimensional transistors.
In addition, the scientists demonstrated the applicability of the structure by assembling it into the logic circuitry of an inverter. This further underscores the technology's ability to lay the foundation for a chemically assembled atomic computer, the scientists say.
"Both of these two-dimensional crystals have been synthesized in the wafer scale in a way that is compatible with current semiconductor manufacturing. By integrating our technique with other growth systems, it's possible that future computing can be done completely with atomically thin crystals
XXX . XXX 4%zero null 0 1 2 3 4 5 6 7 8 Time Travel Jump To over 4 dimensions

Time travel — moving between different points in time — has been a popular topic for science fiction for decades. Franchises ranging from "Doctor Who" to "Star Trek" to "Back to the Future" have seen humans get in a vehicle of some sort and arrive in the past or future, ready to take on new adventures.
The reality, however, is more muddled. Not all scientists believe that time travel is possible. Some even say that an attempt would be fatal to any human who chooses to undertake it.
Understanding time
What is time? While most people think of time as a constant, physicist Albert Einstein showed that time is an illusion; it is relative — it can vary for different observers depending on your speed through space. To Einstein, time is the "fourth dimension." Space is described as a three-dimensional arena, which provides a traveler with coordinates — such as length, width and height —showing location. Time provides another coordinate — direction — although conventionally, it only moves forward. (Conversely, a new theory asserts that time is "real.")

Most physicists think time is a subjective illusion, but what if time is real?
Einstein's theory of special relativity says that time slows down or speeds up depending on how fast you move relative to something else. Approaching the speed of light, a person inside a spaceship would age much slower than his twin at home. Also, under Einstein's theory of general relativity, gravity can bend time.
Picture a four-dimensional fabric called space-time. When anything that has mass sits on that piece of fabric, it causes a dimple or a bending of space-time. The bending of space-time causes objects to move on a curved path and that curvature of space is what we know as gravity.
Both the general and special relativity theories have been proven with GPS satellite technology that has very accurate timepieces on board. The effects of gravity, as well as the satellites' increased speed above the Earth relative to observers on the ground, make the un adjusted clocks gain 38 microseconds a day. (Engineers make calibrations to account for the difference.)
In a sense, this effect, called time dilation, means astronauts are time travelers, as they return to Earth very, very slightly younger than their identical twins that remain on the planet.
Through the time and energy
General relativity also provides scenarios that could allow travelers to go back in time, according to NASA. The equations, however, might be difficult to physically achieve.
One possibility could be to go faster than light, which travels at 186,282 miles per second (299,792 kilometers per second) in a vacuum. Einstein's equations, though, show that an object at the speed of light would have both infinite mass and a length of 0. This appears to be physically impossible, although some scientists have extended his equations and said it might be done.
Time machines
It is generally understood that traveling forward or back in time would require a device — a time machine — to take you there. Time machine research often involves bending space-time so far that time lines turn back on themselves to form a loop, technically known as a "closed time-like curve."

The Doctor's time machine is the TARDIS, which stands for Time and Relative
To accomplish this, time machines often are thought to need an exotic form of matter with so-called "negative energy density." Such exotic matter has bizarre properties, including moving in the opposite direction of normal matter when pushed. Such matter could theoretically exist, but if it did, it might be present only in quantities too small for the construction of a time machine.
However, time-travel research suggests time machines are possible without exotic matter. The work begins with a doughnut-shaped hole enveloped within a sphere of normal matter. Inside this doughnut-shaped vacuum, space-time could get bent upon itself using focused gravitational fields to form a closed time-like curve. To go back in time, a traveler would race around inside the doughnut, going further back into the past with each lap. This theory has a number of obstacles, however. The gravitational fields required to make such a closed time-like curve would have to be very strong, and manipulating them would have to be very precise.
Besides the physics problems, time travel may also come with some unique situations. A classic example is the grandfather paradox, in which a time traveler goes back and kills his parents or his grandfather — the major plot line in the "Terminator" movies — or otherwise interferes in their relationship — think "Back to the Future" — so that he is never born or his life is forever altered.
If that were to happen, some physicists say, you would be not be born in one parallel universe but still born in another. Others say that the photons that make up light prefer self-consistency in timelines, which would interfere with your evil, suicidal plan.
Some scientists disagree with the options mentioned above and say time travel is impossible no matter what your method. The faster-than-light one in particular drew derision from American Museum of Natural History astrophysicist Charles Lu.
That "simply, mathematically, doesn't work," he said in a past interview with sister site LiveScience.
Also, humans may not be able to withstand time travel at all. Traveling nearly the speed of light would only take a centrifuge, but that would be lethal, said Jeff Tollaksen, a professor of physics at Chapman University, in 2012.
Using gravity would also be deadly. To experience time dilation, one could stand on a neutron star, but the forces a person would experience would rip you apart first.
Time travel in fiction
Two 2015 articles by Space.com described different ways in which time travel works in fiction, and the best time-travel machines ever. Some methods used in fiction include:
One-way travel to the future: The traveler leaves home, but the people he or she left behind might age or be dead by the time the traveler returns. Examples: "Interstellar" (2014), "Ikarie XB-1" (1963)
Time travel by moving through higher dimensions: In "Interstellar" (2014), there are "tesseracts" available in which astronauts can travel because the vessel represents time as a dimension of space. A similar concept is expressed in Madeleine L'Engle's "A Wrinkle In Time" (2018, based on the book series that started in 1963), where time is folded by means of a tesseract. The book, however, uses supernatural beings to make the travel possible.
Travelling the space-time vortex: The famous "Doctor Who" (1963-present) TARDIS ("Time And Relative Dimension In Space") uses an extra-dimensional vortex to go through time, while the travelers inside feel time passing normally.
Instantaneous time jumping: Examples include "The Girl Who Leapt Through Time" (2006), the DeLorean from "Back To The Future" (1985), and the Mr. Peabody's WABAC machine from "The Rocky and Bullwinkle Show" (1959-64).
Time travelling while standing still: Both the "Time Machine" (1895 book) and Hermione Granger's Time-Turner from "Harry Potter" keep the traveler still while they move through time.
Slow time travel: In "Primer" (2004), a traveler stays in a box while time traveling. For each minute they want to go back in time, they need to stay in the box for a minute. If they want to go back a day in time, they have to stay there for 24 hours.
Traveling faster than light: In "Superman: The Movie" (1979), Superman flies faster than light to go back in time and rescue Lois Lane before she is killed. The concept was also used in the 1980 novel "Timescape" by Gregory Benford, in which the protagonist sends (hypothetical) faster-than-light tachyon particles back to Earth in 1962 to warn of disaster. In several "Star Trek" episodes and movies, the Enterprise travels through time by going faster than light. In the comic book and TV series "The Flash," the super-speedster uses a cosmic treadmill to travel through time.
Difficult methods to categorize: There's a rocket sled in "Timecop" (1994) that pops in and out of view when it's being used, which has led to much speculation about what's going on. There's also the Time Displacement Equipment in "The Terminator" movie series, which shows off how to fight a war in four dimensions (including time).
So is time travel possible?
While time travel does not appear possible — at least, possible in the sense that the humans would survive it — with the physics that we use today, the field is constantly changing. Advances in quantum theories could perhaps provide some understanding of how to overcome time travel paradoxes.
One possibility, although it would not necessarily lead to time travel, is solving the mystery of how certain particles can communicate instantaneously with each other faster than the speed of light.
In the meantime, however, interested time travelers can at least experience it vicariously through movies, television and book 


++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
MATH <----> HTAM OF TIME DIFFERENCE IN 4 DIMENSION JUMP OVER TO TIME TRAVEL
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++





























































































































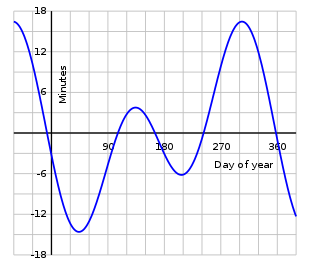
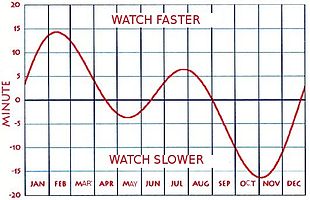




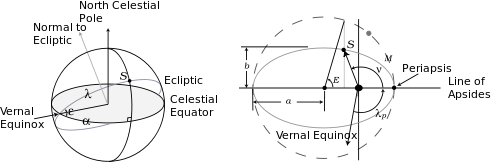

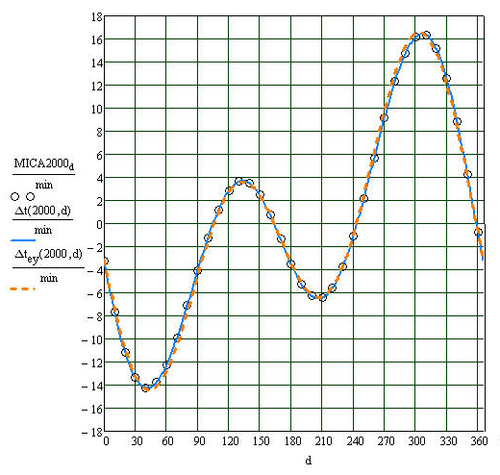


Tidak ada komentar:
Posting Komentar