The motion of objects-frequency conduct Circular Motion

Gerak benda  yang berfrekwensi melakukan Gerak Melingkar 

     

Banyak dalam kehidupan sehari-hari, kita dapat melihat benda-benda yang bergerak melingkar misalnya gerak jarum jam, gerak roda mobil atau motor, putaran baling-baling helicopter, kipas angin, putaran compact disk, rotasi bumi, gerak Roler coaster dan lain-lain yang semuanya memiliki lintasan melingkar. 

 

Secara sederhana, pengertian gerak melingkar adalah gerak sebuah benda dengan lintasan berupa lingkaran. Besaran-besaran Fisika  yang terkait dengan gerak melingkar antara lain periode, frekuensi, posisi sudut, kecepatan sudut, dan percepatan sentripetal. Besaran-besaran inilah yang akan saya bahas selanjutnya didalam Gerak melingkar beraturan

Dalam materi yang saya berikan ini ada 2(dua) gerak melingkar yang akan dibahas, yaitu :

1. A. Gerak Melingkar Beraturan (GMB)
2. B. Gerak Melingkar Berubah Beraturan (GMBB)

   A. Gerak Melingkar Beraturan

   Definisi :
   Gerak Melingkar Beraturan disingkat GMB adalah gerak suatu benda yang lintasannya berbentuk lingkaran dengan ciri-ciri :
3.  Memilik kelajuan tetap, dengan kecepatan linier (v)yang berubah arah sesuai perubahan waktu.
4. Besar dan arah vektor kecepatan sudutnya (ω) tetap, sehingga percepatan sudutnya (α)
   sama dengan nol.
5. Besar percepatan sentripetalnya (a_s) tetap, dengan arah selalu menuju titik pusat
   lingkaran. Istilah sentripetal adalah “yang mencari pusat”. Disebut juga dengan percepatan radial, karena mempunyai arah sepanjang radius, menuju pusat lingkaran

Pada gerak melingkar beraturan. arah kecepatan linier (v) benda setiap saat berubah walaupun besar kecepatan liniernya tetap. Arah kecepatan yang setiap saat berubah ini mengakibatkan adanya percepatan yang senantiasa mengarah ke pusat lingkaran. Percepatan ini disebut dengan Percepatan sentripetal (a_s). Kecepatan sudut (ω) merupakan besaran vektor yang arahnya sama dengan arah perpindahan sudut (θ), yaitu dapat searah atau berlawanan arah dengan arah gerak jarum jam. Perhatikan gambar  berikut ini.. Selanjutnya, beberapa besaran seperti periode, frekuensi, kecepatan linier, dan kecepatan sudut, percepatan dan gaya sentripetal akan kita bahas berikut ini.

1. Frekuensi dan Periode

Benda dikatakan bergerak satu kali putaran penuh jika benda tersebut telah bergerak dari titik A sampai ke titik A lagi.

Frekuensi (f)  adalah banyaknya putaran yang dilakukan benda tiap satuan waktu

Keterangan:
f = frekuensi (Hz)
t = waktu (s)
n = jumlah putaran
Periode (T) adalah waktu yang diperlukan benda untuk melakukan satu kali putaran penuh  dengan bentuk persamaan :

Keterangan:
T = periode (s)
t = waktu (s)
n = jumlah putaran
Hubungan T dengan f adalah:   



    

Contoh soal :

Sebuah roda berputar 60 putaran dalam waktu 10 sekon. Hitung frekuensi dan periode roda tersebut!
Penyelesaian:
Diketahui :
n (jumlah putaran) = 60
t = 10 s
maka :

f = 60/10 =6 Hz    dan   T = 10/60 = 1/6 detik

2. Perpindahan Sudut (θ)

Partikel berpindah dari posisi A ke B, partikel telah menempuh perpindahan sudut θ radian.Besar sudut θ (radian) didefinisikan sebagai :perbandingan antara jarak linier (s) dengan jari jari ditulis :

Keterangan :
θ   = perpindahan sudut  (rad)
S   = jarak yang ditempuh (perpindahan ) benda (m)
R   = jari-jari lingkaran (m)
Untuk 1 putaran = 360^o = 2 π rad
sehingga 1 rad =  360^o / 2 π  = 360^o / 6,28  = 57,3^o

Contoh Soal :

Sebuah roda berjari jari 25 cm berputar, sehingga jarak yang ditempuh oleh titik yang terletak di  tepi roda adalah 1 m. Hitung perpindahan sudutnya!

Penyelesaian:

Jadi perpindahan sudutnya adalah 4 rad

3. Kecepatan Linier dan Kecepatan Sudut

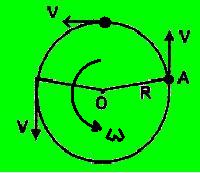
Hubungan antara kecepatan linier dan kecepatan sudut dapat dijelaskan sebagai berikut.

a. Kecepatan linier

Kecepatan linier adalah hasil bagi antara perpindahan yang ditempuh benda dengan selang waktu tempuhnya. Benda yang berputar satu putaran, lintasan yang ditempuh sama dengan keliling lingkaran ( Δ s = 2 π r) dan waktu tempuh T sekon, maka kecepatan linier dirumuskan sebagai berikut.

Keterangan:
v = kecepatan linier (m/s)
r = jari jari lingkaran (m)

b. Kecepatan sudut

Kecepatan sudut adalah besar sudut yang ditempuh dalam selang waktu.
Benda yang berputar satu putaran penuh menempuh sudut 360^o = 2 rr rad dalam waktu
T sekon, maka berlaku :


  
Keterangan:
ω = kecepatan sudut = kecepatan anguler satuannya  rad/s
satuan lain ω = rpm (putaran per menit
dan rps (putaran per sekon)
1 rpm  =  1/60 rps  dan 1 rps = 2π rad
Hubungan antara kecepatan linier (v) dan kecepatan sudut (ω) dinyatakan :

Contoh Soal :

Sebuah roda yang berjari jari 40 cm berputar secara beraturan, dalam 10 sekon roda melakukan 4 kali putaran. Tentukan kecepatan linier dan kecepatan sudut roda tersebut?

Penyelesaian: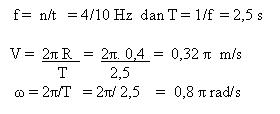   

4. Percepatan Sentripetal (as) dan Gaya Sentripetal (Fs)

Percepatan Sentripetal (a_s) adalah percepatan yang selalu dimiliki suatu benda yang bergerak melingkar dengan arah menuju titik pust lingkaran dan tegak lurus terhadap kecepatan linier v. Peranan percepatan sentripetal (a_s) ini adalah mengubah arah gerak benda (arah kecepatan linear v) sehingga benda tersebut dapat menempuh gerak melingkar.

Persamaan percepatan sentripetal (a_s) ditulis :

Keterangan :

v = kecepatan linier (m/s)
ω = kecepatan sudut (rad/s)
R = jari jari lingkaran (m)
T = periode (s)
f = frekuensi (Hz)

Gaya sentripetal adalah gaya yang arahnya menuju titik pusat lingkaran

Keterangan :

F = gaya Sentripetal  (N)
m= massa benda (kg)
v = kecepatan linier (m/s)
ω = kecepatan sudut (rad/s)
R = jari jari lingkaran (m)

5. Hubungan Roda-roda

a. Untuk dua roda yang dihubungkan sepusat (satu poros), maka arah putaran dan kecepatan sudutnya sama

b. Untuk dua roda yang dihubungkan bersinggungan, arah putaran keduanya berlawanan dan   kecepatan liniernya sama.

c.   Untuk dua roda yang dihubungkan dengan tali atau rantai, arah putaran keduanya dan kelajuan tinier keduanya adalah sama.

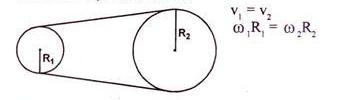
Jika roda-roda I dan II pada gambar b dan c diatas adalah roda-roda bergerigi, sehingga mengalami pemindahan putaran roda gigi yang jumlah giginya berturut-turut n₁ dan n₂ dengan kecepatan sudutnya  ω₁, dan ω₂ , maka dapat dirumuskan:

Contoh Soal :

Roda B dan C sepusat dan saling melekat. Roda A dan roda B dihubungkan dengan rantai yang masing-masing roda memiliki jari-jari RA = 20 cm, Rb = 15 cm, Rc = 40 cm. Jika roda C berputar 120 rpm, maka tentukan kecepatan sudut roda A!

Penyelesaian:
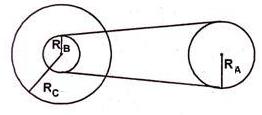
ω _c  = 120 putaran /menit =  120/60 put/s   =  2 put/s    =  2. 2π rad/s   =   4π  rad/s
Roda B dan C sepusat maka  ω _c   =  ω _b  =  4π  rad/s
Roda A dan roda B dihubungkan dengan rantai, maka :
V_A           =    V_B
ω_A . R_A   =    ω_B.  R_B
ω_A.               =    ω_B.  R_B/ R_A 
=    4π  . 15/20
=    3π   rad/s

Soal-Soal Latihan 1 :

1. Sebuah roda sepeda berputar seperti gambar berikut.

Katup ban tersebut dapat berputar 60 kali dalam 15 s. Maka periode dan frekuensi gerak katup tersebut adalah…

A. 15 sekon dan 15 Hz

B.  15 sekon dan 4 Hz

C.   4 sekon dan  4 Hz

D.   4 sekon dan  ¼ Hz

E.   ¼ sekon dan 4 Hz

Jawab : E.

2. Dari soal no. 1 dapat diketahui banyaknya putaran setelah t = 20 sekon adalah… A. 120 putaran B. 100 putaran C. 80 putaran D. 60 putaran E. 40 putaran Jawab : … 3. Rado memacu sepeda motornya pada lintasan yang berbentuk lingkaran dalam waktu 1 jam. Dalam waktu tersebut, dengan lintasan yang memiliki diameter 300 meter Rado telah melakukan 120 putaran. maka periode dan frekuensi gerak sepeda motor Rado adalah… A. 30 sekon dan 1/30 Hz B. 60 sekon dan 1/60 Hz C. 80 sekon dan 1/80 Hz D. 120 sekon dan 1/120 Hz E. 200 sekon dan 1/200 Hz Jawab : … 4. Dari soal nomor 3, maka kecepatan linier yang dimiliki sepeda motor Rado adalah.. A. 5,0 π m/s B. 7,5 π m/s C. 10,0 π m/s D. 12,5 π m/s E. 15,0 π m/s Jawab : … 5. Suatu benda berputar dengan kecepatan sudut 10 rad/s. Kecepatanya linier suatu titik pada benda berjarak 0,5m dari sumbu putar adalah … A. 20 m/s B. 10,5 m/s C. 10 m/s D. 9,5 m/s E. 5,0 m/s Jawab : … 6. Sebuah benda melakukan 150 kali putaran selama 0,25 jam, besar periode putarannya adalah … A. 60 sekon B. 12 sekon C. 6 sekon D. 1/6 sekon E. 1/60 sekon Jawab : … 7. Jarum speedometer sebuah mobil menunjukkan angka 1200 rpm, ini berarti kecepatan sudut perputaran mesin mobil tersebut adalah… A. 20 rad/s B. 20 π rad/s C. 40 rad/s D. 40 π rad/s E. 60 π rad/s Jawab : … 8. Sebuah sepeda motor berbelok mengelilingi suatu lintasan melingkar dengan diameter 40 m dengan kelajuan tetap 10 m/s. Percepatan sentripetal sepeda motor adalah … A. nol B. 5 m/s2 menuju pusat C. 5 m/s2 menjauhi pusat D. 10 m/s2 menuju pusat E. 10 m/s2 menjauhi pusat Jawab: … 9. Suatu percobaan gerak melingkar beraturan yang dilakukan sekelompok siswa diperoleh data seperti tabel di bawah ini : M (kg) R (m) Waktu 10 putaran (s) Waktu 20 putaran (s) Waktu 30 putaran (s) 0,15 1 4 8 12 Berdasarkan tabel tersebut dapat disimpulkan percepatan sentripetal dalam percobaan ini adalah . . A. 25 π2 ms-2 B. 15 π2ms-2 C. 10 π2 ms– 2 D. 5,0 π 2 ms-2 E. 2,5 π 2 ms-2 Jawab : … 10. Dua buah roda dihubungkan dengan sebuah rantai 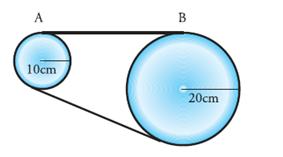Roda A berjari-jari 10 cm dan roda B berjari-jari 20 cm. Jika roda A berputar dengan kecepatan sudut 8 rad/s, kecepatan sudut roda B adalah . . . . A. 16 rad/s B. 12 rad/s C. 8 rad/s D. 6 rad/s E. 4 rad/s Jawab : … 11. Roda B dan C sepusat dan saling melekat. Roda A dan roda B dihubungkan dengan rantai yang masing-masing roda memiliki jari-jari Ra = 25 cm, Rb = 20 cm, Rc = 45 cm. Jika roda C berputar 150 rpm, maka kecepatan sudut roda A adalah… A. 4π rad/s B. 8π rad/s C. 10π rad/s D. 20π rad/s E. 25π rad/s Jawab : … 12. Dari soal nomor 11, maka kecepatan linier Roda A adalah : A. 1,5 π m/s B. 1,25π m/s C. 1,0π m/s D. 0,75 π m/s E. 0,50 π m/s Jawab. …

B. Gerak Melingkar Berubah Beraturan

Definisi :

Gerak Melingkar Berubah Beraturan disingkat GMBB adalah gerak suatu benda dengan bentuk lintasan melingkar dengan ciri-ciri :

• 1. Besar percepatan sudut/anguler (α) konstan. Jika perecepatan anguler (α) benda searah dengan perubahan kecepatan anguler maka gerak putaran benda semakin cepat, dan gerak putaran benda semakin lambat bila percepatan anguler berlawanan arah dengan perubahan kecepatan anguler benda.
• 2.  Memiliki percepatan tangensial (a_t). Pada gerak melingkar beraturan (GMB) hanya memiliki percepatan sentripetal, tetapi tidak mempunyai percepatan tangensial (a_t) = 0 ).

Untuk mempelajari Gerak Melingkar Berubah Beraturan (GMBB), ada beberapa percepatan yang terdapat didalam GMBB yaitu :

• 1. Percepatan Sentripetal (a_s)
  2. Percepatan Anguler (α)
  3. Percepatan Tangensial (a_t)
  4. Percepatan total (a total)

1. Percepatan Sentripetal (as)

Percepatan sentripetal (a_s) adalah percepatan yang selalu dimiliki suatu benda yang bergerak melingkar dengan arah menuju titik pust lingkaran dan tegak lurus terhadap kecepatan linier (v). Pada gerak melingkar beraturan (GMB), walaupun ada percepatan sentripetal (a_s), besar kecepatan liniernya tidak berubah. Dalam hal ini, peranan percepatan sentripetal (as) adalah mengubah arah kecepatan linear (v) benda, sehingga benda tersebut dapat menempuh gerak melingkar. Istilah sentripetal adalah “yang mencari pusat”. Disebut juga dengan percepatan radial, karena mempunyai arah sepanjang radius, menuju pusat lingkaran. Persamaan percepatan sentripetal (a_s) dapat ditulis :

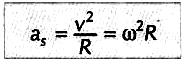
Keterangan :

• a_s = percepatan sentripetal (m/s²)
• v = kelajuan linier (m/s)
• ω = kecepatan sudut (rad/s)
• R = jari-jari lintasan benda (m)

2. Percepatan Anguler / Sudut (α)

Pada GMBB, besar kecepatan sudut yang dimiliki suatu benda tidaklah tetap. Misalnya, gerak Gerinda yang berputar, kemudian mesinnya dimatikan, maka geraknya akan mengalami penurunan kecepatan sudutnya hingga berhenti. Perubahan kecepatan sudut tiap satu satuan waktu inilah yang dinamakan percepatan sudut.

Gbr. mesin gerinda tangan. capture gbr dari http://darikami.perkakasku.com

Percepatan Sudut (α) didefinikan sebagai perubahan kecepatan sudut (∆ω) dalam selang waktu (∆t) sehingga persamaan Percepatan Sudut (α) dapat ditulis :

Keterangan :

• α = percepatan sudut/anguler (rad/s²)
• ∆ω = ω2 – ω1 = perubahan kecepatan sudut (rad/s)
• ∆t = t2 – t1 = selang waktu (s)

3. Percepatan Tangensial (at)

Semua benda bergerak melingkar selalu memiliki percepatan sentripetal (a_s), tetapi belum tentu memiliki percepatan tangensial (a_t).  Percepatan tangensial (a_t) didefinisikan sebagai perubahan kecepatan linier (∆v) dalam selang waktu (∆t). Arah vektor percepatan tangensial (a_t) adalah sama dengan arah kecepatan linier (v) dan menyinggung sisi tepi lingkaran tegak lurus dengan arah vektor percepatan sentripetal (a_s).

Percepatan tangensial (a_t) atau percepatan linier ini berperan mengubah kecepatan linear benda. Benda yang bergerak melingkar beraturan (GMB) hanya memiliki percepatan sentripetal (a_s) tetapi tidak mempunyai percepatan tangensial (a_t)=0 ). Dalam GMBB, kecepatan linearnya dapat berubah secara beraturan akibat adanya suatu gaya yang disebut gaya tangensial. Gaya ini mengakibatkan adanya percepatan tangensial (a_t) yang arahnya berimpit dengan kecepatan linier.

Persamaan percepatan tangensial (a_t) dapat ditulis :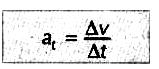

Hubungan antara percepatan sudut (α) dengan percepatan tangensial (a_t) dinyatakan dengan persamaan berikut:

Keterangan :

•  v = kecepatan linier (m/s)
• ∆v = v2 –v1 = perubahan kecepatan linier (m/s)
• ω = kecepatan sudut (rad/s)
• ∆ω = ω2 – ω1 = perubahan kecepatan sudut (rad/s)
• ∆t = t2 – t1 = selang waktu (s)
• a_{t  =}  percepatan tangensial
• α = percepatan sudut/anguler (rad/s²)
• R = jari-jari lingkaran

4. Percepatan Total (a)

Dalam gerak melingkar berubah beraturan (GMBB), percepatan tangensial (a_t) mempunyai arah yag sama dengan vektor kecepatan linier (v) yang tegak lurus dengan percepatan sentripetal (a_s). Dengan demikian percepatan tangensial (a_t) tegak lurus dengan percepatan sentripetal (a_s). Arah vektor kedua percepatan tersebut dapat dilihat pada gambar dibawah ini

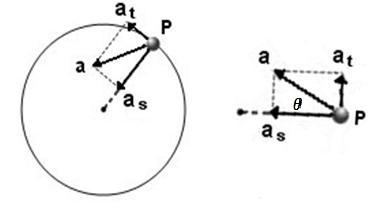
Dari gambar diperoleh persamaan Percepatan total benda dititik P yang melakukan GMBB, yaitu Resultan vector dari percepatan tangensial (a_t) dan percepatan sentripetal (a_s).

Dengan arah vektor resultan :
Keterangan:

• a= percepatan total (m/s²)
• a_s= percepatan sentripetal (m/s²)
• a_t= percepatan tangensial (m/s²)

Dalam Modul sebelumnya mengenai Gerak lurus berubah beraturan (GLBB), maka persamaan Gerak Melingkar Berubah Beraturan (GMBB) analog dengan GLBB

Keterangan :

• Θ = perpindahan sudut (rad)
• ω_o = kecepatan sudut awal (rad/s)
• ω_t = kecepatan sudut setelah t sekon (rad/s)
• α = percepatan sudut (rad/s²)
• t = waktu (s)

Contoh soal GLBB

1. Sebuah roda mula-mula berputar dengan kecepatan sudut 50 rad/s. Suatu gesekan kecil pada poros putaran roda yang berjari-jari 20 cm menyebabkan suatu perlambatan sudut tetap sehingga roda tersebut akhirnya berhenti dalam waktu 5 sekon.
Tentukan :
a. Percepatan sudut roda,br/>
b. Jarak yang telah ditempuh roda dari mulai bergerak sampai berhenti ,br/>
Pembahasan :
Diketahui :

• ω_o = 50 rad/s
• ω_t = 0 rad/s
• t = 5 s
• R = 20 cm= 0,2 m

Ditanya :

• a. α
• b. x

Jawab :

• a.             α = ( 0 – 50 ) / 5 = – 10 rad/s²

• b.      θ  = ω_o .t + ½ α. t²
•               = 50. 5 + ½. ( -10 ). 5² = 250 – 125 = 125 rad
•          X = θ. R ²
•              = 125. 0,2 = 25 m

2. Sebuah baling-baling dengan jari-jari putar 1 meter awalnya diam, kemudian berputar dengan percepatan sudut konstan 2 rad/s².
Tentukan :
kecepatan sudut (ω_t )baling-baling pada saat t = 4 sekon.
Pembahasan :
Diketahui :
Ditanya : kecepatan sudut (ωt) setelah 2 sekon
Jawab :
Kecepatan sudut setelah 2 sekon

• ω_t  = ω_o + α.t
• ω_t  = 0 + 2.5
• ω_t  = 10 rad/

3.  Sebuah roda berjari-jari 0,5 m bergerak dari keadaan diam hingga pada saat t = 5 s kecepatan sudutnya (ω) = 15,0 rad/s
Tentukan :

• a. Besar percepatan total
  b. Sudut yang dibentuk percepatan total terhadap arah radial

Pembahasan :
Diketahui : R = 0,5 m t = 5 s dan ωt = 15,0 rad/s
Ditanya :  (a).  a  dan   (b).  θ
Jawab :

soal Pesawat tempur  :

Sebuah pesawat tempur terbang dari sebuah pangkalan angkatan darat pada arah 30^O timur dari utara sejauh 100 km, kemudian berbelok kearah timur sejauh 40√3 dan akhirnya berbelok kearah selatan sejauh 40 km. (lihat gbr)
Maka besar perpindahan pesawat tempur tersebut dari pangkalan angkatan darat adalah…

A. 540 m
B. 350 m
C. 270 m
D. 180 m
E. 160 m

 ^{akibat akibat terjadinya frekwensi dan getaran yang terjadi pada benda dan zat maka akan terjadi perubahan wujud benda dan zat sebagai berikut :}

Perubahan wujud Zat