Jenis-jenis irisan kerucut
Jika sebuah bidang mengiris kerucut sejajar dengan satu dan hanya satu generator, maka irisannya adalah parabola. Jika bidang pengiris sejajar dengan dua generator, maka irisannya akan memotong kedua kulit dan membentuk sebuah hiperbola. Sebuah elips terjadi jika bidang pengiris tidak sejajar dengan generator mana pun. Lingkaran adalah kasus khusus dari elips, yang terbentuk jika bidang pengiris memotong semua generator dan tegak lurus sumbu kerucut.Kasus degenerasi
Kasus-kasus degenerasi terjadi jika bidang-bidang pengiris melalui verteks kerucut. Irisan-irisannya dapat berupa titik, garis lurus, dan dua garis lurus yang saling berpotongan. Sebuah titik terjadi jika bidang pengiris melalui verteks kerucut namun tidak memotong generator mana pun. Kasus ini merupakan elips yang terdegenerasi. Jika bidang pengiris melalui verteks kerucut, dan hanya satu generator, maka yang terjadi adalah sebuah garis lurus, dan merupakan parabola yang terdegenerasi. Sebuah hiperbola terdegenerasi terjadi jika bidang pengiris melalui verteks kerucut dan dua generator sehingga memberikan dua garis lurus yang saling berpotongan.Geometri analitis
Secara geometri analitis, irisan kerucut dapat didefinisikan sebagai:| “ | tempat kedudukan titik-titik pada sebuah bidang, sedemikian, sehingga jarak titik-titik tersebut ke sebuah titik tetap F (yang disebut fokus) memiliki rasio yang konstan terhadap jarak titik-titik tersebut ke sebuah garis tetap L (disebut direktriks) yang tidak mengandung F[1]. | ” |
Eksentrisitas adalah rasio antara FM dan M'M. Elips (e=1/2), parabola (e=1) dan hiperbola (e=2) dengan fokus (F) dan direktriks yang tetap.
Koordinat Kartesius
Dalam koordinat kartesius, grafik dari persamaan kuadrat dengan dua variabel selalu menghasilkan irisan kerucut, dan semua irisan kerucut dapat dihasilkan dengan cara ini.Jika terdapat persamaan dengan bentuk:
- Jika h2 = ab, persamaan ini menghasilkan parabola.
- Jika h2 < ab, persamaan ini menghasilkan elips.
- Jika h2 > ab, persamaan ini menghasilkan hiperbola.
- Jika a = b and h = 0, persamaan ini menghasilkan lingkaran.
- Jika a + b = 0, persamaan ini menghasilkan hiperbola persegi.
Irisan Kerucut dalam matematika
merupakan lokus dari semua titik yang membentuk kurva dua dimensi,
dimana kurva tersebut terbentuk dari irisan sebuah kerucut dengan sebuah
bidang. Terdapat 4 macam irisan kerucut, yaitu lingkaran, parabola,
elips serta hiperbola.
DEFINISI
LingkaranLingkaran merupakan tempat kedudukan titik-titik yang berjarak sama terhadap suatu titik tertentu.
- Titik tertentu itu disebut pusat lingkaran
- Jarak yang sama itu disebut jari-jari/radius (r)
Contoh gambar:
Lingkaran dengan pusat (0, 0) dan jari-jari 2

Parabola
Parabola merupakan tempat kedudukan titik-titik yang berjarak sama terhadap sebuah titik dan sebuah garis tertentu.
- Titik itu disebut fokus/titik api (F)
- Garis tertentu itu disebut garis direktris/garis arah
- Garis yang melalui F dan tegak lurus dengan garis arah disebut sumbu simetri parabola
- Titik potong parabola dengan sumbu simetri disebut puncak parabola
- Tali busur terpendek yang melalui F disebut Latus Rectum → tegak lurus dengan sumbu simetri
Parabola horisontal dengan puncak (0,0), fokus (1, 0), dan garis arah x = –1

Parabola vertikal dengan puncak (0,0), fokus (0, 1), dan garis arah y = –1

Elips
(1) Elips merupakan tempat kedudukan titik-titik yang jumlah jaraknya terhadap 2 titik tertentu tetap.
- Jumlah jarak itu = 2a (untuk elips horisontal) atau 2b (untuk elips vertikal)
- Kedua titik tetap itu disebut fokus (F) → jarak antara F1 dan F2 adalah 2c
- Titik itu adalah fokus (F), dan garis itu adalah garis arah.
- Ruas garis yang melalui kedua fokus dan memotong elips disebut sumbu mayor
- Pusat elips adalah titik tengah F1 dan F2
- Ruas garis yang melalui pusat, tegak lurus sumbu mayor dan memotong elips disebut sumbu minor
Contoh gambar:
Elips horisontal dengan pusat (0, 0), puncak-puncak (5, 0), (–5, 0), (0, 4), (0, –4), fokus (3, 0), (–3, 0), dan garis arah x = ±25/3

Elips vertikal dengan pusat (0, 0), puncak-puncak (√2, 0), (–√2, 0), (0, 2), (0, –2), fokus (0,√2), (0, –√2), dan garis arah y = ±2√2/3

Hiperbola
(1) Hiperbola merupakan tempat kedudukan titik-titik yang selisih jaraknya terhadap 2 titik tertentu tetap
- Selisih jarak itu = 2a (untuk elips horisontal) atau 2b (untuk elips vertikal)
- Kedua titik tetap itu disebut fokus (F) → jarak antara F1 dan F2 adalah 2c
- Titik-titik tertentu itu disebut fokus (F1 dan F2)
- Garis yang melalui titik-titik F1 dan F2 disebut sumbu transvers (sumbu utama)/ sumbu nyata
- Titik tengah F1 dan F2 disebut pusat hiperbola (P)
- Garis yang melalui P dan tegak lurus sumbu transvers disebut sumbu konjugasi (sumbu sekawan)/ sumbu imajiner
- Titik-titik potong hiperbola dan sumbu transvers disebut puncak hiperbola
- Garis yang melalui fokus dan tegak lurus pada sumbu nyata dan memotong hiperbola di 2 titik → ruas garis penghubung kedua titik tersebut = Latus Rectum
Hiperbola horisontal dengan pusat (0, 0), puncak (2, 0), (–2, 0), fokus (√6, 0), (–√6, 0), dan asimtot y = ± ½√2 x

Hiperbola vertikal dengan pusat (0, 0), puncak (√2, 0), (–√2, 0), fokus (0, √6), (0, –√6), dan asimtot y = ± ½√2 x

PERSAMAAN

Perhatikan beberapa Tips berikut ini :
Cara membedakan persamaan-persamaan irisan kerucut:
- Pada persamaan Lingkaran: koefisien x2 dan y2 sama
- Pada persamaan Parabola: hanya salah satu yang bentuknya kuadrat (x2 saja atau y2 saja)
- Pada persamaan Elips: koefisien x2 dan y2 bertanda sama (sama-sama positif atau sama-sama negatif)
- Pada persamaan Hiperbola: koefisien x2 dan y2 berbeda tanda (salah satu positif, yang lain negatif)
- 3x2 + 3y2 + 6x + y = 5 → Persamaan Lingkaran
- 3x2 + 3y + 6x = 5 → Persamaan Parabola
- 3x2 + y2 + 6x + y = 5 → Persamaan Elips
- 3x2 – 3y2 + 6x + y = 5 → Persamaan Hiperbola
KEDUDUKAN TITIK TERHADAP IRISAN KERUCUT
Dalam mencari kedudukan titik terhadap irisan kerucut dapat menggunakan cara sebagai berikut :- Jadikan ruas kanan pada persamaan irisan kerucut = 0
- Masukkan koordinat titik pada persamaan:
→ Jika hasil ruas kiri = 0 → titik berada tepat pada irisan kerucut tersebut
→ Jika hasil ruas kanan > 0 → titik berada di luar irisan kerucut
Contoh:
Tentukanlah kedudukan titik (5, –1) terhadap elips dengan persamaan 3x2 + y2 + 6x + y = 5?
Penyelesaian :
3x2 + y2 + 6x + y – 5 = 0
Ruas kiri: 3.52 + (–1)2 + 6.5 + (–1) – 5 = 75 + 1 + 30 – 1 – 5 =100
→ 100 > 0, jadi titik (5, –1) berada di luar elips tersebut
KEDUDUKAN GARIS TERHADAP IRISAN KERUCUT
Dalam mencari kedudukan garis terhadap irisan kerucut dapat digunakan cara berikut ini.- Persamaan garis dijadikan persamaan x = … atau y = …
- Substitusikan persamaan garis itu pada persamaan irisan kerucut, sehingga menghasilkan suatu persamaan kuadrat.
- Hitung nilai Diskriminan (D) dari persamaan kuadrat tersebut (Ingat! D = b2 – 4.a.c)
→ Jika D = 0 → garis menyinggung irisan kerucut di 1 titik
→ Jika D > 0 → garis memotong irisan kerucut di 2 titik
Contoh:
Tentukanlah kedudukan garis x + 2y = 4 terhadap parabola dengan persamaan 3x2 + 3y + 6x = 5
Penyelesaian :
Garis: x = 4 – 2y
3(4 – 2y)2 + 3y + 6(4 – 2y) – 5 = 0
3(16 – 16y + 4y2) + 3y + 24 – 12y – 5 = 0
48 – 48y + 12y2 + 3y + 24 – 12y – 5 = 0
12y2 – 57y + 67 = 0
D = b2 – 4.a.c = (–57)2 – 4.12.67 = 33
Karena D > 0 maka garis x + 2y = 4 memotong parabola tersebut
PERSAMAAN GARIS SINGGUNG

dalam hal ini m merupakan gradien.
Persamaan garis singgung pada titik (x1, y1)
Dalam menyelesaikan persamaan garis singgung ini selalu gunakanlah sistem bagi adil, dimana
(…)2 menjadi (…).(…)
(…) menjadi ½ (…) + ½ (…)
Pada salah satu (…) titik ke persamaan hasil bagi adil akan dimasukkan koordinat titik yang diketahui
- Jika titik terletak pada irisan kerucut, akan menghasilkan persamaan garis singgung
- Jika titik terletak di luar irisan kerucut, akan menghasilkan persamaan garis polar
Selanjutnya masukkan kedua titik potong itu ke dalam persamaan hasil bagi adil untuk mendapatkan 2 buah persamaan garis singgung
Untuk lebih jelasnya perhatikan beberapa contoh berikut :
Contoh 1:
Tentukanlah persamaan garis singgung pada lingkaran x2 + y2 + 4x = 13 pada titik (2, 1)?
Jawab :
(2, 1) terletak pada lingkaran (22 + 12 + 4.2 = 13)
Persamaan bagi adil:
x1.x + y1.y + 2.x1 + 2.x = 9
Masukkan (2, 1) sebagai x1 dan y1:
2.x + 1.y + 2.2 + 2.x = 9
4x + y – 5 = 0 → persamaan garis singgung
Contoh 2:
Tentukanlah persamaan garis singgung pada lingkaran x2 + y2 + 4x = 13 pada titik (4, 1)?
Jawab :
(4, 1) terletak di luar lingkaran (42 + 12 + 4.4 = 33 > 16)
Persamaan bagi adil:
x1.x + y1.y + 2.x1 + 2.x = 9
Masukkan (4, 1) sebagai x1 dan y1:
4.x + 1.y + 2.4 + 2.x = 9
6x + y – 1 = 0 → persamaan garis polar
y = 1 – 6x
Substitusikan persamaan garis polar ke dalam persamaan lingkaran:
x2 + (1 – 6x)2 + 4x – 13 = 0
x2 + 1 – 12x + 36x2 + 4x – 13 = 0
37x2 – 8x – 12 = 0
Selanjutnya gunakan rumus abc untuk mencari akar-akarnya:

Masukkan (x1, y1) dan (x2, y2) ke dalam persamaan hasil bagi adil


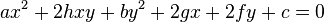

Tidak ada komentar:
Posting Komentar