advanced Telescope theory and electronics microscope on the space and timer galaxy AMNIMARJESLOW GOVERNMENT 91220017 LORD IN LOR ELECTRONIC PAST -- NOW --- GOING FUTURE TELESCOPE AND MICROSCOPE INSTRUMENTATION AND CONTROLLING RAW TO READ AND WRITE 02096010014 LJBUSAF XAMNI$$$$$ 27 $ WOW I AM YES TO JESS

History and Quantum Mechanical Quantities

The Photoelectric Effect

Electrons are emitted from matter that is absorbing energy from electromagnetic radiation, resulting in the photoelectric effect.

Learning Objectives

Explain how the photoelectric effect paradox was solved by Albert Einstein.

Key Takeaways

KEY POINTS

• The energy of the emitted electrons depends only on the frequency of the incident light, and not on the light intensity.
• Einstein explained the photoelectric effect by describing light as composed of discrete particles.
• Study of the photoelectric effect led to important steps in understanding the quantum nature of light and electrons, which would eventually lead to the concept of wave-particle duality.

KEY TERMS

black body radiation: The type of electromagnetic radiation within or surrounding a body in thermodynamic equilibrium with its environment, or emitted by a black body (an opaque and non-reflective body) held at constant, uniform temperature.
photoelectron: Electrons emitted from matter by absorbing energy from electromagnetic radiation.
wave-particle duality: A postulation that all particles exhibit both wave and particle properties. It is a central concept of quantum mechanics.

Electrons are emitted from matter when light shines on a surface . This is called the photoelectric effect, and the electrons emitted in this manner are called photoelectrons.
The photoelectric effect typically requires photons with energies from a few electronvolts to 1 MeV for heavier elements, roughly in the ultraviolet and X-ray range. Study of the photoelectric effect led to important steps in understanding the quantum nature of light and electrons and influenced the formation of the concept of wave-particle du

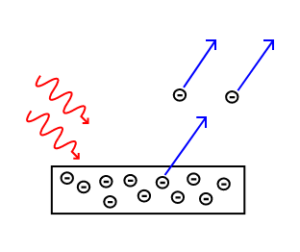
The Photoelectric Effect: Electrons are emitted from matter by absorbed light.

ality. The photoelectric effect is also widely used to investigate electron energy levels in matter.

Photoelectric Effect: A brief introduction to the Photoelectric Effect and electron photoemission.
Heinrich Hertz discovered the photoelectric effect in 1887. Although electrons had not been discovered yet, Hertz observed that electric currents were produced when ultraviolet light was shined on a metal. By the beginning of the 20th century, physicists confirmed that:

• The energy of the individual photoelectrons increased with the frequency (or color) of the light, but was independent of the intensity (or brightness) of the radiation.
• The photoelectric current was determined by the light’s intensity; doubling the intensity of the light doubled the number of emitted electrons.

This observation was very puzzling to many physicists. At the time, light was accepted as a wave phenomenon. Since energy carried by a wave should only depend on its amplitude (and not on the frequency of the wave), the frequency dependence of the emitted electrons’ energies didn’t make sense.
In 1905, Albert Einstein solved this apparent paradox by describing light as composed of discrete quanta (now called photons), rather than continuous waves. Building on Max Planck’s theory of black body radiation, Einstein theorized that the energy in each quantum of light was equal to the frequency multiplied by a constant h, later called Planck’s constant. A photon above a threshold frequency has the required energy to eject a single electron, creating the observed effect. As the frequency of the incoming light increases, each photon carries more energy, hence increasing the energy of each outgoing photoelectron. By doubling the number of photons as the intensity is doubled, the number of photelectrons should double accordingly.
According to Einstein, the maximum kinetic energy of an ejected electron is given by ${\text{K}}_{\text{max}}=\text{hf}-\varphi$ , where $\text{h}$ is the Planck constant and f is the frequency of the incident photon. The term $\varphi$ is known as the work function, the minimum energy required to remove an electron from the surface of the metal. The work function satisfies $\varphi ={\text{hf}}_0$ , where ${\text{f}}_0$ is the threshold frequency for the metal for the onset of the photoelectric effect. The value of work function is an intrinsic property of matter.
Is light then composed of particles or waves? Young’s experiment suggested that it was a wave, but the photoelectric effect indicated that it should be made of particles. This question would be resolved by de Broglie: light, and all matter, have both wave-like and particle-like properties.

Photon Energies of the EM Spectrum

The electromagnetic (EM) spectrum is the range of all possible frequencies of electromagnetic radiation.

Learning Objectives

Compare photon energy with the frequency of the radiation

Key Takeaways

KEY POINTS

• Electromagnetic radiation is classified according to wavelength, divided into radio waves, microwaves, terahertz (or sub-millimeter) radiation, infrared, the visible region humans perceive as light, ultraviolet, X-rays, and gamma rays.
• Photon energy is proportional to the frequency of the radiation.
• Most parts of the electromagnetic spectrum are used in science for spectroscopic and other probing interactions as ways to study and characterize matter.

KEY TERMS

• Planck constant: a physical constant that is the quantum of action in quantum mechanics. It has a unit of angular momentum. The Planck constant was first described as the proportionality constant between the energy of a photon (unit of electromagnetic radiation) and the frequency of its associated electromagnetic wave in his derivation of the Planck’s law
• Maxwell’s equations: A set of equations describing how electric and magnetic fields are generated and altered by each other and by charges and currents.

The Electromagnetic Spectrum

The electromagnetic (EM) spectrum is the range of all possible frequencies of electromagnetic radiation . The electromagnetic spectrum extends from below the low frequencies used for modern radio communication to gamma radiation at the short-wavelength (high-frequency) end, thereby covering wavelengths of thousands of kiilometers down to those of a fraction of the size of an atom (approximately an angstrom). The limit for long wavelengths is the size of the universe itself.

Electromagnetic spectrum: This shows the electromagnetic spectrum, including the visible region, as a function of both frequency (left) and wavelength (right).

Maxwell’s equations predicted an infinite number of frequencies of electromagnetic waves, all traveling at the speed of light. This was the first indication of the existence of the entire electromagnetic spectrum. Maxwell’s predicted waves included waves at very low frequencies compared to infrared, which in theory might be created by oscillating charges in an ordinary electrical circuit of a certain type. In 1886, the physicist Hertz built an apparatus to generate and detect what are now called radio waves, in an attempt to prove Maxwell’s equations and detect such low-frequency electromagnetic radiation. Hertz found the waves and was able to infer (by measuring their wavelength and multiplying it by their frequency) that they traveled at the speed of light. Hertz also demonstrated that the new radiation could be both reflected and refracted by various dielectric media, in the same manner as light.

Filling in the Electromagnetic Spectrum

In 1895, Wilhelm Röntgen noticed a new type of radiation emitted during an experiment with an evacuated tube subjected to a high voltage. He called these radiations ‘X-rays’ and found that they were able to travel through parts of the human body but were reflected or stopped by denser matter such as bones. Before long, there were many new uses for them in the field of medicine.
The last portion of the electromagnetic spectrum was filled in with the discovery of gamma rays. In 1900, Paul Villard was studying the radioactive emissions of radium when he identified a new type of radiation that he first thought consisted of particles similar to known alpha and beta particles, but far more penetrating than either. However, in 1910, British physicist William Henry Bragg demonstrated that gamma rays are electromagnetic radiation, not particles. In 1914, Ernest Rutherford (who had named them gamma rays in 1903 when he realized that they were fundamentally different from charged alpha and beta rays) and Edward Andrade measured their wavelengths, and found that gamma rays were similar to X-rays, but with shorter wavelengths and higher frequencies.
The relationship between photon energy and the radiation’s frequency and wavelength is illustrated as the following equilavent equation: $\nu =\frac{\text{c}}{\lambda },\text{or}\nu =\frac{\text{E}}{\text{h}}\text{or}\text{E}=\frac{\text{hc}}{\lambda }$ , where $\nu$ is the frequency, $\lambda$ is the wavelength, $\text{E}$ is photon energy, $\text{c}$ is the speed of light, and $\text{h}$ is the Planck constant. Generally, electromagnetic radiation is classified by wavelength into radio waves, microwaves, terahertz (or sub-millimeter) radiation, infrared, the visible region humans perceive as light, ultraviolet, X-rays, and gamma rays. The behavior of EM radiation depends on its wavelength. When EM radiation interacts with single atoms and molecules, its behavior also depends on the amount of energy per quantum (photon) it carries.
Most parts of the electromagnetic spectrum are used in science for spectroscopic and other probing interactions as ways to study and characterize matter. Also, radiation from various parts of the spectrum has many other uses in communications and manufacturing.

Energy, Mass, and Momentum of Photon

A photon is an elementary particle, the quantum of light, which carries momentum and energy.

Learning Objectives

State physical properties of a photon

Key Takeaways

KEY POINTS

• $\text{E}=\text{h}\nu$ Energy of photon is proportional to its frequency.
• $\text{p}=\text{h}\text{k}$ Momentum of photon is proportional to the wave vector.
• Photon’s rest mass is 0.

KEY TERMS

• black body radiation: The type of electromagnetic radiation within or surrounding a body in thermodynamic equilibrium with its environment, or emitted by a black body (an opaque and non-reflective body) held at constant, uniform temperature.
• elementary particle: a particle not known to have any substructure
• photoelectric effect: The occurrence of electrons being emitted from matter (metals and non-metallic solids, liquids, or gases) as a consequence of their absorption of energy from electromagnetic radiation.

A photon is an elementary particle, the quantum of light. It has no rest mass and has no electric charge. The modern photon concept was developed gradually by Albert Einstein to explain experimental observations of the photoelectric effect, which did not fit the classical wave model of light. In particular, the photon model accounted for the frequency dependence of light’s energy. Max Planck explained black body radiation using semiclassical models, in which light is still described by Maxwell’s equations, but the material objects that emit and absorb light, do so in amounts of energy that are quantized.
Photons are emitted in many natural processes. They are emitted from light sources such as floor lamps or lasers . For example, when a charge is accelerated it emits photons, a phenomenon known as synchrotron radiation. During a molecular, atomic or nuclear transition to a lower or higher energy level, photons of various energy will be emitted or absorbed respectively. A photon can also be emitted when a particle and its corresponding antiparticle are annihilated. During all these processes, photons will carry energy and momentum.

laser: Photons emitted in a coherent beam from a laser.

Energy of photon: From the studies of photoelectric effects, energy of a photon is directly proportional to its frequency with the Planck constant being the proportionality factor. Therefore, we already know that $\text{E}=\text{h}\nu$ (Eq. 1), where $\text{E}$ is the energy and $\nu$ is the frequency.
Momentum of photon: According to the theory of Special Relativity, energy and momentum (p) of a particle with rest mass m has the following relationship: ${\text{E}}^2=({\text{mc}}^2{)}^2+{\text{p}}^2{\text{c}}^2$ , where $\text{c}$ is the speed of light. In the case of a photon with zero rest mass, we get $\text{E}=\text{pc}$ . Combining this with Eq. 1, we get $\text{p}=\frac{\text{h}\nu }{\text{c}}=\frac{\text{h}}{\lambda }$ . Here, $\lambda$ is the wavelength of the light. Since momentum is a vector quantity and p points in the direction of the photon’s propagation, we can write $\text{p}=\text{h}\text{k}$ , where $\text{h}=\frac{\text{h}}{2\pi }$ and is $\text{k}$ a wave vector.
You may wonder how an object with zero rest mass can have nonzero momentum. This confusion often arises because of the commonly used form of momentum ($\text{mv}$ in non-relativistic mechanics and $\gamma \text{mv}$ in relativistic mechanics, where $\text{v}$ is velocity and $\gamma =\frac{1}{\sqrt{1-\frac{{\text{v}}^2}{{\text{c}}^2}}}$ . ) This formula, obviously, shouldn’t be used in the case $\text{v}=\text{c}$ .

Implications of Quantum Mechanics

Quantum mechanics has had enormous success in explaining microscopic systems and has become a foundation of modern science and technology.

Learning Objectives

Explain importance of quantum mechanics for technology and other branches of science

Key Takeaways

KEY POINTS

• A great number of modern technological inventions are based on quantum mechanics, including the laser, the transistor, the electron microscope, and magnetic resonance imaging.
• Quantum mechanics is also critically important for understanding how individual atoms combine covalently to form molecules. The application of quantum mechanics to chemistry is known as quantum chemistry.
• Researchers are currently seeking robust methods of directly manipulating quantum states for applications in computer and information science.

KEY TERMS

• cryptography: the practice and study of techniques for secure communication in the presence of third parties
• relativistic quantum mechanics: a theoretical framework for constructing quantum mechanical models of fields and many-body systems
• string theory: an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity

The field of quantum mechanics has been enormously successful in explaining many of the features of our world. The behavior of the subatomic particles (electrons, protons, neutrons, photons, and others) that make up all forms of matter can often be satisfactorily described only using quantum mechanics. Quantum mechanics has also strongly influenced string theory.
Quantum mechanics is also critically important for understanding how individual atoms combine covalently to form molecules. The application of quantum mechanics to chemistry is known as quantum chemistry. Relativistic quantum mechanics can, in principle, mathematically describe most of chemistry. Quantum mechanics can also provide quantitative insight into ionic and covalent bonding processes by explicitly showing which molecules are energetically favorable to which other molecules and the magnitudes of the energies involved. Furthermore, most of the calculations performed in modern computational chemistry rely on quantum mechanics.
A great number of modern technological inventions operate on a scale where quantum effects are significant. Examples include the laser , the transistor (and thus the microchip), the electron microscope, and magnetic resonance imaging (MRI). The study of semiconductors led to the invention of the diode and the transistor, which are indispensable parts of modern electronic systems and devices.

Laser: Red (635-nm), green (532-nm), and blue-violet (445-nm) lasers

Researchers are currently seeking robust methods of directly manipulating quantum states. Efforts are being made to more fully develop quantum cryptography, which will theoretically allow guaranteed secure transmission of information. A more distant goal is the development of quantum computers, which are expected to perform certain computational tasks exponentially faster than classical computers. Another topic of active research is quantum teleportation, which deals with techniques to transmit quantum information over arbitrary distances.

Particle-Wave Duality

Wave–particle duality postulates that all physical entities exhibit both wave and particle properties.

Learning Objectives

Describe experiments that demonstrated wave-particle duality of physical entities

Key Takeaways

KEY POINTS

• All entities in Nature behave as both a particle and a wave, depending on the specifics of the phenomena under consideration.
• Particle-wave duality is usually hidden in macroscopic phenomena, conforming to our intuition.
• In the double-slit experiment of electrons, individual event displays a particle-like property of localization (or a “dot”). After many repetitions, however, the image shows an interference pattern, which indicates that each event is in fact governed by a probability distribution.

KEY TERMS

• Maxwell’s equations: A set of equations describing how electric and magnetic fields are generated and altered by each other and by charges and currents.
• black body: An idealized physical body that absorbs all incident electromagnetic radiation, regardless of frequency or angle of incidence. Although black body is a theoretical concept, you can find approximate realizations of black body in nature.
• photoelectric effects: In photoelectric effects, electrons are emitted from matter (metals and non-metallic solids, liquids or gases) as a consequence of their absorption of energy from electromagnetic radiation.

Wave–particle duality postulates that all physical entities exhibit both wave and particle properties. As a central concept of quantum mechanics, this duality addresses the inability of classical concepts like “particle” and “wave” to fully describe the behavior of (usually) microscopic objects.
From a classical physics point of view, particles and waves are distinct concepts. They are mutually exclusive, in the sense that a particle doesn’t exhibit wave-like properties and vice versa. Intuitively, a baseball doesn’t disappear via destructive interference, and our voice cannot be localized in space. Why then is it that physicists believe in wave-particle duality? Because that’s how mother Nature operates, as they have learned from several ground-breaking experiments. Here is a short, chronological list of those experiments:

• Young’s double-slit experiment: In the early Nineteenth century, the double-slit experiments by Young and Fresnel provided evidence that light is a wave. In 1861, James Clerk Maxwell explained light as the propagation of electromagnetic waves according to the Maxwell’s equations.
• Black body radiation: In 1901, to explain the observed spectrum of light emitted by a glowing object, Max Planck assumed that the energy of the radiation in the cavity was quantized, contradicting the established belief that electromagnetic radiation is a wave.
• Photoelectric effect: Classical wave theory of light also fails to explain photoelectric effect. In 1905, Albert Einstein explained the photoelectric effects by postulating the existence of photons, quanta of light energy with particulate qualities.
• De Broglie’s wave (matter wave): In 1924, Louis-Victor de Broglie formulated the de Broglie hypothesis, claiming that all matter, not just light, has a wave-like nature. His hypothesis was soon confirmed with the observation that electrons (matter) also displays diffraction patterns, which is intuitively a wave property.

From these historic achievements, physicists now accept that all entities in nature behave as both a particle and a wave, depending on the specifics of the phenomena under consideration. Because of its counter-intuitive aspect, the meaning of the particle-wave duality is still a point of debate in quantum physics. The standard interpretation is that the act of measurement causes the set of probabilities, governed by a probability distribution function acquired from a “wave”, to immediately and randomly assume one of the possible values, leading to a “particle”-like result.
So, why do we not notice a baseball acting like a wave? The wavelength of the matter wave associated with a baseball, say moving at 95 miles per hour, is extremely small compared to the size of the ball so that wave-like behavior is never noticeable.

Diffraction Revisited

De Broglie’s hypothesis was that particles should show wave-like properties such as diffraction or interference.

Learning Objectives

Compare application of X-ray, electron, and neutron diffraction for materials research

Key Takeaways

KEY POINTS

• The wavelength of an electron is given by the de Broglie equation $\lambda =\frac{\text{h}}{\text{p}}$ .
• Because of different forms of interaction involved, X-ray, electron, and neutron are suitable for different studies of material properties.
• De Broglie’s idea completed the wave-particle duality.

KEY TERMS

• photoelectric effect: The observation of electrons being emitted from matter (metals and non-metallic solids, liquids, or gases) as a consequence of their absorption of energy from electromagnetic radiation.
• black body radiation: The type of electromagnetic radiation within or surrounding a body in thermodynamic equilibrium with its environment, or emitted by a black body (an opaque and non-reflective body) held at constant, uniform temperature.
• grating: Any regularly spaced collection of essentially identical, parallel, elongated elements.

The de Broglie hypothesis, formulated in 1924, predicts that particles should also behave as waves. The wavelength of an electron is given by the de Broglie equation $\lambda =\frac{\text{h}}{\text{p}}$ . Here $\text{h}$ is Planck’s constant and $\text{p}$ the relativistic momentum of the electron. $\lambda$ is called the de Broglie wavelength.
From the work by Planck (black body radiation) and Einstein (photoelectric effect), physicists understood that electromagnetic waves sometimes behaved like particles. De Broglie’s hypothesis is complementary to this idea: particles should also show wave-like properties such as diffraction or interference. De Broglie’s formula was confirmed three years later for electrons (which have a rest-mass) with the observation of electron diffraction in two independent experiments. George Paget Thomson passed a beam of electrons through a thin metal film and observed the predicted interference patterns. Clinton Joseph Davisson and Lester Halbert Germerguided their beam through a crystalline grid to observe diffraction patterns.
X-ray diffraction is a commonly used tool in materials research. Thanks to the wave-particle duality, matter wave diffraction can also be used for this purpose. The electron, which is easy to produce and manipulate, is a common choice. A neutron is another particle of choice. Due to the different kinds of interactions involved in the diffraction processes, the three types of radiation (X-ray, electron, neutron) are suitable for different kinds of studies.
Electron diffraction is most frequently used in solid state physics and chemistry to study the crystalline structure of solids. Experiments are usually performed using a transmission electron microscope or a scanning electron microscope. In these instruments, electrons are accelerated by an electrostatic potential in order to gain the desired energy and, thus, wavelength before they interact with the sample to be studied. The periodic structure of a crystalline solid acts as a diffraction grating, scattering the electrons in a predictable manner. Working back from the observed diffraction pattern, it is then possible to deduce the structure of the crystal producing the diffraction pattern. Unlike other types of radiation used in diffraction studies of materials, such as X-rays and neutrons, electrons are charged particles and interact with matter through the Coulomb forces. This means that the incident electrons feel the influence of both the positively charged atomic nuclei and the surrounding electrons. In comparison, X-rays interact with the spatial distribution of the valence electrons, while neutrons are scattered by the atomic nuclei through the strong nuclear force.

Electron Diffraction Pattern:  Typical electron diffraction pattern obtained in a transmission electron microscope with a parallel electron beam.

Neutrons have also been used for studying crystalline structures. They are scattered by the nuclei of the atoms, unlike X-rays, which are scattered by the electrons of the atoms. Thus, neutron diffraction has some key differences compared to more common methods using X-rays or electrons. For example, the scattering of X-rays is highly dependent on the atomic number of the atoms (i.e., the number of electrons), whereas neutron scattering depends on the properties of the nuclei. In addition, the magnetic moment of the neutron is non-zero, and can thus also be scattered by magnetic fields. This means that neutron scattering is more useful for determining the properties of atomic nuclei, despite the fact that neutrons are significantly harder to create, manipulate, and detect compared to X-rays and electrons.

The Wave Function

A wave function is a probability amplitude in quantum mechanics that describes the quantum state of a particle and how it behaves.

Learning Objectives

Relate the wave function with the probability density of finding a particle, commenting on the constraints the wave function must satisfy for this to make sense

Key Takeaways

KEY POINTS

• $|\psi |2\left(\text{x}\right)$ corresponds to the probability density of finding a particle in a given location x at a given time.
• The laws of quantum mechanics (the Schrödinger equation) describe how the wave function evolves over time. The Schrödinger equation is a type of wave equation, which explains the name “wave function”.
• A wave function must satisfy a set of mathematical constraints for the calculations and physical interpretation to make sense.

KEY TERMS

Schrödinger equation: A partial-differential that describes how the quantum state of some physical system changes with time. It was formulated in late 1925 and published in 1926 by the Austrian physicist Erwin Schrödinger
harmonic oscillator: a system that, when displaced from its equilibrium position, experiences a restoring force $\text{F}$ proportional to the displacement $\text{x}$

In quantum mechanics, a wave function is a probability amplitude describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers. For a single particle, it is a function of space and time. The most common symbols for a wave function are $\psi \left(\text{x}\right)$ or $\Psi \left(\text{x}\right)$ (lowercase or uppercase psi, respectively), when the wave function is given as a function of position $\text{x}$ . Although $\psi$ is a complex number, $|\psi |2$ is a real number and corresponds to the probability density of finding a particle in a given place at a given time, if the particle’s position is measured.

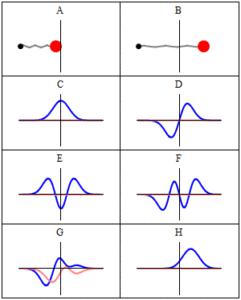
Trajectories of a Harmonic Oscillator: This figure shows some trajectories of a harmonic oscillator (a ball attached to a spring) in classical mechanics (A-B) and quantum mechanics (C-H). In quantum mechanics (C-H), the ball has a wave function, which is shown with its real part in blue and its imaginary part in red. The trajectories C-F are examples of standing waves, or “stationary states. ” Each standing-wave frequency is proportional to a possible energy level of the oscillator. This “energy quantization” does not occur in classical physics, where the oscillator can have any energy.

The laws of quantum mechanics (the Schrödinger equation) describe how the wave function evolves over time. The wave function behaves qualitatively like other waves, such as water waves or waves on a string, because the Schrödinger equation is mathematically a type of wave equation. This explains the name “wave function” and gives rise to wave-particle duality.
The wave function must satisfy the following constraints for the calculations and physical interpretation to make sense:

• It must everywhere be finite.
• It must everywhere be a continuous function and continuously differentiable.
• It must everywhere satisfy the relevant normalization condition so that the particle (or system of particles) exists somewhere with 100-percent certainty.

If these requirements are not met, it’s not possible to interpret the wave function as a probability amplitude. This is because the values of the wave function and its first order derivatives may not be finite and definite (having exactly one value), which means that the probabilities can be infinite and have multiple values at any one position and time, which is nonsense. Furthermore, when we use the wave function to calculate an observation of the quantum system without meeting these requirements, there will not be finite or definite values to use (in this case the observation can take a number of values and can be infinite). This is not a possible occurrence in a real-world experiment. Therefore, a wave function is meaningful only if these conditions are satisfied.

de Broglie and the Wave Nature of Matter

The concept of “matter waves” or “de Broglie waves” reflects the wave-particle duality of matter.

Learning Objectives

Formulate the de Broglie relation as an equation

Key Takeaways

KEY POINTS

• de Broglie relations show that the wavelength is inversely proportional to the momentum of a particle.
• The Davisson-Germer experiment demonstrated the wave-nature of matter and completed the theory of wave-particle duality.
• Experiments demonstrated that de Broglie hypothesis is applicable to atoms and macromolecules.

KEY TERMS

• diffraction: The bending of a wave around the edges of an opening or an obstacle.
• special relativity: A theory that (neglecting the effects of gravity) reconciles the principle of relativity with the observation that the speed of light is constant in all frames of reference.
• wave-particle duality: A postulation that all particles exhibit both wave and particle properties. It is a central concept of quantum mechanics.

In quantum mechanics, the concept of matter waves (or de Broglie waves) reflects the wave-particle duality of matter. The theory was proposed by Louis de Broglie in 1924 in his PhD thesis. The de Broglie relations show that the wavelength is inversely proportional to the momentum of a particle, and is also called de Broglie wavelength.
Einstein derived in his theory of special relativity that the energy and momentum of a photon has the following relationship:
$\text{E}=\text{pc}$ ($\text{E}$ : energy, $\text{p}$ : momentum, $\text{c}$ : speed of light).
He also demonstrated, in his study of photoelectric effects, that energy of a photon is directly proportional to its frequency, giving us this equation:
$\text{E}=\text{h}\nu$ ($\text{h}$ : Planck constant, $\nu$ : frequency).
Combining the two equations, we can derive a relationship between the momentum and wavelength of light:
$\text{p}=\frac{\text{E}}{\text{c}}=\frac{\text{h}\nu }{\text{c}}=\frac{\text{h}}{\lambda }$ . Therefore, we arrive at $\lambda =\frac{\text{h}}{\text{p}}$ .
De Broglie’s hypothesis is that this relationship $\lambda =\frac{\text{h}}{\text{p}}$ , derived for electromagnetic waves, can be adopted to describe matter (e.g. electron, neutron, etc.) as well.
De Broglie didn’t have any experimental proof at the time of his proposal. It took three years for Clinton Davisson and Lester Germer to observe diffraction patterns from electrons passing a crystalline metallic target (see ). Before the acceptance of the de Broglie hypothesis, diffraction was a property thought to be exhibited by waves only. Therefore, the presence of any diffraction effects by matter demonstrated the wave-like nature of matter. This was a pivotal result in the development of quantum mechanics. Just as the photoelectric effect demonstrated the particle nature of light, the Davisson–Germer experiment showed the wave-nature of matter, thus completing the theory of wave-particle duality.

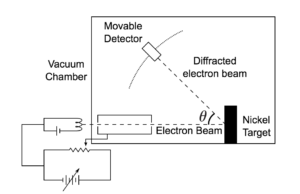
Davisson-Germer Experimental Setup: The experiment included an electron gun consisting of a heated filament that released thermally excited electrons, which were then accelerated through a potential difference (giving them a certain amount of kinetic energy towards the nickel crystal). To avoid collisions of the electrons with other molecules on their way towards the surface, the experiment was conducted in a vacuum chamber. To measure the number of electrons that were scattered at different angles, an electron detector that could be moved on an arc path about the crystal was used. The detector was designed to accept only elastically scattered electrons.

Experiments with Fresnel diffraction and specular reflection of neutral atoms confirm the application to atoms of the de Broglie hypothesis. Further, recent experiments confirm the relations for molecules and even macromolecules, normally considered too large to undergo quantum mechanical effects. In 1999, a research team in Vienna demonstrated diffraction for molecules as large as fullerenes. The researchers calculated a De Broglie wavelength of the most probable ${\text{C}}_{60}$ velocity as 2.5 pm.

The Heisenberg Uncertainty Principle

The uncertainty principle asserts a basic limit to the precision with which some physical properties of a particle can be known simultaneously.

Learning Objectives

Relate the Heisenberg uncertainty principle with the matter wave nature of all quantum objects

Key Takeaways

KEY POINTS

• The uncertainty principle is inherent in the properties of all wave-like systems, and that it arises in quantum mechanics is simply due to the matter wave nature of all quantum objects.
• The uncertainty principle is not a statement about the observational success of current technology.
• The more precisely the position of some particle is determined, the less precisely its momentum can be known, and vice versa. This can be formulated as the following inequality: ${\sigma }_{\text{x}}{\sigma }_{\text{y}}\ge \frac{\overline{\text{h}}}{2}$ .

KEY TERMS

• matter wave: A concept reflects the wave-particle duality of matter. The theory was proposed by Louis de Broglie.
• Rayleigh criterion: The angular resolution of an optical system can be estimated from the diameter of the aperture and the wavelength of the light, which was first proposed by Lord Rayleigh.

The uncertainty principle is any of a variety of mathematical inequalities, asserting a fundamental limit to the precision with which certain pairs of physical properties of a particle, such as position $\text{x}$ and momentum $\text{p}$ or energy $\text{E}$ and time $\text{t}$ , can be known simultaneously. The more precisely the position of some particle is determined, the less precisely its momentum can be known, and vice versa. This can be formulated as the following inequality: ${\sigma }_{\text{x}}{\sigma }_{\text{y}}\ge \frac{\overline{\text{h}}}{2}$ , where ${\sigma }_{\text{x}}$ is the standard deviation of position, σp is the standard deviation of momentum, and [latex]\bar{\text{h}}=\frac{\text{h}}{2π}[/latex]. The uncertainty principle is inherent in the properties of all wave-like systems, and it arises in quantum mechanics simply due to the matter wave nature of all quantum objects. Thus, the uncertainty principle actually states a fundamental property of quantum systems, and is not a statement about the observational success of current technology.
The principle is quite counterintuitive, so the early students of quantum theory had to be reassured that naive measurements to violate it were bound always to be unworkable. One way in which Heisenberg originally illustrated the intrinsic impossibility of violating the uncertainty principle is by using an imaginary microscope as a measuring device.

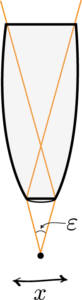
Heisenberg Microscope: Heisenberg’s microscope, with cone of light rays focusing on a particle with angle $ϵ$ He imagines an experimenter trying to measure the position and momentum of an electron by shooting a photon at it.

Examples

Example One

If the photon has a short wavelength and therefore a large momentum, the position can be measured accurately. But the photon scatters in a random direction, transferring a large and uncertain amount of momentum to the electron. If the photon has a long wavelength and low momentum, the collision does not disturb the electron’s momentum very much, but the scattering will reveal its position only vaguely.

Example Two

If a large aperture is used for the microscope, the electron’s location can be well resolved (see Rayleigh criterion); but by the principle of conservation of momentum, the transverse momentum of the incoming photon and hence the new momentum of the electron resolves poorly. If a small aperture is used, the accuracy of both resolutions is the other way around.

Heisenberg’s Argument

Heisenberg’s argument is summarized as follows. He begins by supposing that an electron is like a classical particle, moving in the $\text{x}$ direction along a line below the microscope, as in the illustration to the right. Let the cone of light rays leaving the microscope lens and focusing on the electron makes an angle $\epsilon$ with the electron. Let $\lambda$ be the wavelength of the light rays. Then, according to the laws of classical optics, the microscope can only resolve the position of the electron up to an accuracy of $\delta \text{x}=\frac{\lambda }{\sin \left(\epsilon /2\right)}$ When an observer perceives an image of the particle, it’s because the light rays strike the particle and bounce back through the microscope to their eye. However, we know from experimental evidence that when a photon strikes an electron, the latter has a recoil with momentum proportional to $\text{h}/\lambda$ , where $\text{h}$ is Planck’s constant.
It is at this point that Heisenberg introduces objective indeterminacy into the thought experiment. He writes that “the recoil cannot be exactly known, since the direction of the scattered photon is undetermined within the bundle of rays entering the microscope”. In particular, the electron’s momentum in the $\text{x}$ direction is only determined up to $\delta {\text{p}}_{\text{x}}\approx \frac{\text{h}}{\lambda }\sin \left(\epsilon /2\right)$ . Combining the relations for $\delta \text{x}$ and $\delta {\text{p}}_{\text{x}}$ , we thus have that $\delta \text{x}\cdot \delta {\text{p}}_{\text{x}}\approx \left(\frac{\lambda }{\sin \left(\epsilon /2\right)}\right)\left(\frac{\text{h}}{\lambda }\sin \left(\epsilon /2\right)\right)=\text{h}$ , which is an approximate expression of Heisenberg’s uncertainty principle.

Heisenberg Uncertainty Principle Derived and Explained
One of the most-oft quoted results of quantum physics, this doozie forces us to reconsider what we can know about the universe. Some things cannot be known simultaneously. In fact, if anything about a system is known perfectly, there is likely another characteristic that is completely shrouded in uncertainty. So significant figures ARE important after all!

Philosophical Implications

Since its inception, many counter-intuitive aspects of quantum mechanics have provoked strong philosophical debates.

Learning Objectives

Formulate the Copenhagen interpretation of the probabilistic nature of quantum mechanics

Key Takeaways

KEY POINTS

• According to the Copenhagen interpretation, the probabilistic nature of quantum mechanics is intrinsic in our physical universe.
• When quantum wave function collapse occurs, physical possibilities are reduced into a single possibility as seen by an observer.
• Once a particle in an entangled state is measured and its state is determined, the Copenhagen interpretation demands that the state of the other entangled particle is also determined instantaneously.

KEY TERMS

• probability density function: Any function whose integral over a set gives the probability that a random variable has a value in that set.
• Bell’s theorem: A no-go theorem famous for drawing an important line in the sand between quantum mechanics (QM) and the world as we know it classically. In its simplest form, Bell’s theorem states: No physical theory of local hidden variables can ever reproduce all of the predictions of quantum mechanics.
• epistemological: Of or pertaining to epistemology or theory of knowledge, as a field of study.

Since its inception, many counter-intuitive aspects and results of quantum mechanics have provoked strong philosophical debates and many interpretations. Even fundamental issues, such as Max Born’s basic rules interpreting $\psi \ast \psi$ as a probability density function took decades to be appreciated by society and many leading scientists. Indeed, the renowned physicist Richard Feynman once said, “I think I can safely say that nobody understands quantum mechanics. ”

The Copenhagen Interpretation

The Copenhagen interpretation—due largely to the Danish theoretical physicist Niels Bohr, shown in —remains a quantum mechanical formalism that is widely accepted amongst physicists, some 75 years after its enunciation. According to this interpretation, the probabilistic nature of quantum mechanics is not a temporary feature which will eventually be replaced by a deterministic theory, but instead must be considered a final renunciation of the classical idea of causality.

Niels Bohr and Albert Einstein: Niels Bohr (left) and Albert Einstein (right). Despite their pioneering contributions to the inception of the quantum mechanics, they disagreed on its interpretation.

The Copenhagen interpretation has philosophical implications to the concept of determinism. According to the theory of determinism, for everything that happens there are conditions such that, given those conditions, nothing else could happen. Determinism and free-will seem to be mutually exclusive. If the universe, and any person in it are governed by strict and universal laws , then that means that a person’s behavior could be predicted based on sufficient knowledge of the circumstances obtained prior to that person’s behavior. However, the Copenhagen interpretation suggests a universe in which outcomes are not fully determined by prior circumstances but also by probability. This gave thinkers alternatives to strictly bound possibilities, proposing a model for a universe that follows general rules but never had a predetermined future.

Philosophical Implications

It is also believed therein that any well-defined application of the quantum mechanical formalism must always make reference to the experimental arrangement. This is due to the quantum mechanical principle of wave function collapse. That is, a wave function which is initially in a superposition of several different possible states appears to reduce to a single one of those states after interaction with an observer. In simplified terms, it is the reduction of the physical possibilities into a single possibility as seen by an observer. This raises philosophical questions about whether something that is never observed actually exists.

Einstein-Podolsky-Rosen (EPR) Paradox

Albert Einstein (shown in , himself one of the founders of quantum theory) disliked this loss of determinism in measurement in the Copenhagen interpretation. Einstein held that there should be a local hidden variable theory underlying quantum mechanics and, consequently, that the present theory was incomplete. He produced a series of objections to the theory, the most famous of which has become known as the Einstein-Podolsky-Rosen (EPR) paradox. John Bell showed by Bell’s theorem that this “EPR” paradox led to experimentally testable differences between quantum mechanics and local realistic theories. Experiments have been performed confirming the accuracy of quantum mechanics, thereby demonstrating that the physical world cannot be described by any local realistic theory. The Bohr-Einstein debates provide a vibrant critique of the Copenhagen Interpretation from an epistemological point of view.

Quantum Entanglement

One of the most bizarre aspect of the quantum mechanics is known as quantum entanglement. Quantum entanglement occurs when particles interact physically and then become separated, while isloated from the rest of the universe to prevent any deterioration of the quantum state. According to the Copenhagen interpretation of quantum mechanics, their shared state is indefinite until measured. Once a particle in the entangled state is measured and its state is determined, the Copenhagen interpretation demands that the other particles’ state is also determined instantaneously. This bizarre nature of action at a distance (which seemingly violate the speed limit on the transmission of information implicit in the theory of relativity) is what bothered Einstein the most. (According to the theory of relativity, nothing can travel faster than the speed of light in a vacuum. This seemingly puts a limit on the speed at which information can be transmitted. ) Quantum entanglement is the key element in proposals for quantum computers and quantum teleportation.

Applications of Quantum Mechanics

Fluorescence and Phosphorescence

Fluorescence and phosphorescence are photoluminescence processes in which material emits photons after excitation.

Learning Objectives

Compare mechanisms of fluorescence and phosphorescence light emission

Key Takeaways

Key Points

• The emitted light usually has a longer wavelength, and therefore lower energy, than the absorbed radiation.
• Fluorescence occurs when an orbital electron of a molecule or atom relaxes to its ground state by emitting a photon of light after being excited to a higher quantum state by some type of energy.
• In a phosphorescence, excitation of electrons to a higher state is accompanied with the change of a spin state. Relaxation is a slow process since it involves energy state transitions “forbidden” in quantum mechanics.

Key Terms

• spin: A quantum angular momentum associated with subatomic particles; it also creates a magnetic moment.
• photon: The quantum of light and other electromagnetic energy, regarded as a discrete particle having zero rest mass, no electric charge, and an indefinitely long lifetime.
• ground state: the stationary state of lowest energy of a particle or system of particles

Fluorescence and Phosphorescence

Fluorescence is the emission of light by a substance that has absorbed light or other electromagnetic radiation. It is a form of photoluminescence. In most cases, the emitted light has a longer wavelength, and therefore lower energy, than the absorbed radiation. However, when the absorbed electromagnetic radiation is intense, it is possible for one electron to absorb two photons; this two-photon absorption can lead to emission of radiation having a shorter wavelength than the absorbed radiation. The emitted radiation may also be of the same wavelength as the absorbed radiation, termed “resonance fluorescence”.
Fluorescence occurs when an orbital electron of a molecule or atom relaxes to its ground state by emitting a photon of light after being excited to a higher quantum state by some type of energy. The most striking examples of fluorescence occur when the absorbed radiation is in the ultraviolet region of the spectrum, and thus invisible to the human eye, and the emitted light is in the visible region.

Fluorescence: Fluorescent minerals emit visible light when exposed to ultraviolet light

Phosphorescence is a specific type of photoluminescence related to fluorescence. Unlike fluorescence, a phosphorescent material does not immediately re-emit the radiation it absorbs. Excitation of electrons to a higher state is accompanied with the change of a spin state. Once in a different spin state, electrons cannot relax into the ground state quickly because the re-emission involves quantum mechanically forbidden energy state transitions. As these transitions occur very slowly in certain materials, absorbed radiation may be re-emitted at a lower intensity for up to several hours after the original excitation.

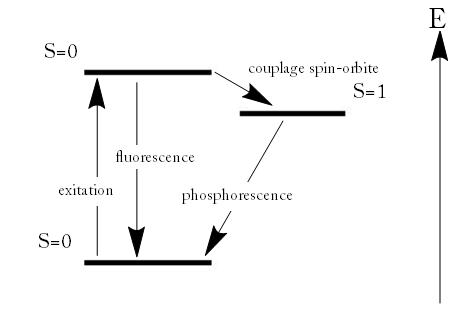
Fluorescence and Phosphorescence: Energy scheme used to explain the difference between fluorescence and phosphorescence

Commonly seen examples of phosphorescent materials are the glow-in-the-dark toys, paint, and clock dials that glow for some time after being charged with a bright light such as in any normal reading or room light. Typically the glowing then slowly fades out within minutes (or up to a few hours) in a dark room.

Phosphorescence: Phosphorescent material glowing in the dark.

Lasers

A laser is a device that emits monochromatic light through a process of optical amplification based on the stimulated emission of photons.

Learning Objectives

Identify process that generates laser emission and the defining characteristics of laser light

Key Takeaways

Key Points

• Principles of laser operation are largely based on quantum mechanics, most importantly on the process of the stimulated emission of photons.
• Spontaneous emission is a random decaying process. The phase associated with the emitted photon is also random.
• Atomic transition can be stimulated by the presence of an incoming photon at a frequency associated with the atomic transition. This process leads to optical amplification as an identical photon is emitted along with the incoming photon.

Key Terms

• free-electron laser: a laser that use a relativistic electron beam as the lasing medium, which moves freely through a magnetic structure
• monochromatic: Describes a beam of light with a single wavelength (i.e., of one specific color or frequency).
• coherence: an ideal property of waves that enables stationary (i.e., temporally and spatially constant) interference

A laser is a device that emits monochromatic light (electromagnetic radiation ). It does so through a process of optical amplification based on the stimulated emission of photons. The term “laser” originated as an acronym for Light Amplification by Stimulated Emission of Radiation. Laser is distinct from other light sources for its high degree of spatial and temporal coherence, which means that laser outputs a narrow beam that maintains its temporal-phase relationship.
Principles of laser operation are largely based on quantum mechanics. (One exception would be free-electron lasers, whose operation can be explained solely by classical electrodynamics. ) When an electron is excited from a lower-energy to a higher-energy level, it will not stay that way forever. An electron in an excited state may decay to an unoccupied lower-energy state according to a particular time constant characterizing that transition. When such an electron decays without external influence, it emits a photon; this process is called “spontaneous emission. ” The phase associated with the emitted photon is random. A material with many atoms in an excited state may thus result in radiation that is very monochromatic, but the individual photons would have no common phase relationship and would emanate in random directions. This is the mechanism of fluorescence and thermal emission.
However, an external photon at a frequency associated with the atomic transition can affect the quantum mechanical state of the atom. As the incident photon passes by, the rate of transitions of the excited atom can be significantly enhanced beyond that due to spontaneous emission. This “induced” decay process is called stimulated emission. In stimulated emission, the decaying atom produces an identical “copy” of the incoming photon. Therefore, after the atom decays, we have two identical outgoing photons. Since there was only one incoming photon, we amplified the intensity of light by a factor of 2!

Stimulated Photon Emission: In stimulated emission process, a photon (with a frequency equal to the atomic transition) encounters an excited atom, and a new photon identical to the incoming photon is produced. The result is an atom in the ground state with two outgoing photons.

Holography

Holography is an optical technique which enables three-dimensional images to be made.

Learning Objectives

Explain how holographic images are recorded and their properties

Key Takeaways

Key Points

• When the two laser beams reach the recording medium, their light waves intersect and interfere with each other. It is this interference pattern that is imprinted on the recording medium.
• When a reconstruction beam illuminates the hologram, it is diffracted by the hologram’s surface pattern. This produces a light field identical to the one originally produced by the scene and scattered onto the hologram.
• Holographic image changes as the position and orientation of the viewing system changes in exactly the same way as if the object were still present, thus making the image appear three-dimensional.

Key Terms

• interference: An effect caused by the superposition of two systems of waves, such as a distortion on a broadcast signal due to atmospheric or other effects.
• laser: A device that produces a monochromatic, coherent beam of light.
• silver halide: The light-sensitive chemicals used in photographic film and pape

Holography is a technique which enables three-dimensional images to be made. It involves the use of a laser, interference, diffraction, light intensity recording and suitable illumination of the recording. The image changes as the position and orientation of the viewing system changes in exactly the same way as if the object were still present, thus making the image appear three-dimensional.
Laser: Holograms are recorded using a flash of light that illuminates a scene and then imprints on a recording medium, much in the way a photograph is recorded. In addition, however, part of the light beam must be shone directly onto the recording medium – this second light beam is known as the reference beam (]). A hologram requires a laser as the sole light source. Laser is required as a light source to produce an interference pattern on the recording plate. To prevent external light from interfering, holograms are usually taken in darkness, or in low level light of a different color from the laser light used in making the hologram. Holography requires a specific exposure time, which can be controlled using a shutter, or by electronically timing the laser

Recording a hologram: Holograms are recorded using a flash of light that illuminates a scene and then imprints on a recording medium, much in the way a photograph is recorded. In addition, however, part of the light beam must be shone directly onto the recording medium – this second light beam is known as the reference beam.

Apparatus: A hologram can be made by shining part of the light beam directly onto the recording medium, and the other part onto the object in such a way that some of the scattered light falls onto the recording medium. A more flexible arrangement for recording a hologram requires the laser beam to be aimed through a series of elements that change it in different ways. The first element is a beam splitter that divides the beam into two identical beams, each aimed in different directions:

• One beam (known as the illumination or object beam) is spread using lenses and directed onto the scene using mirrors. Some of the light scattered (reflected) from the scene then falls onto the recording medium.
• The second beam (known as the reference beam) is also spread through the use of lenses, but is directed so that it doesn’t come in contact with the scene, and instead travels directly onto the recording medium.

Reconstructing a hologram: An interference pattern can be considered an encoded version of a scene, requiring a particular key – the original light source – in order to view its contents. This missing key is provided later by shining a laser, identical to the one used to record the hologram, onto the developed film. When this beam illuminates the hologram, it is diffracted by the hologram’s surface pattern. This produces a light field identical to the one originally produced by the scene and scattered onto the hologram

Several different materials can be used as the recording medium. One of the most common is a film very similar to photographic film (silver halide photographic emulsion), but with a much higher concentration of light-reactive grains, making it capable of the much higher resolution that holograms require. A layer of this recording medium (e.g. silver halide) is attached to a transparent substrate, which is commonly glass, but may also be plastic.
Process: When the two laser beams reach the recording medium, their light waves intersect and interfere with each other. It is this interference pattern that is imprinted on the recording medium. The pattern itself is seemingly random, as it represents the way in which the scene’s light interfered with the original light source – but not the original light source itself. The interference pattern can be considered an encoded version of the scene, requiring a particular key – the original light source – in order to view its contents.
This missing key is provided later by shining a laser, identical to the one used to record the hologram, onto the developed film. When this beam illuminates the hologram, it is diffracted by the hologram’s surface pattern. This produces a light field identical to the one originally produced by the scene and scattered onto the hologram. The image this effect produces in a person’s retina is known as a virtual image.

The Periodic Table of Elements

A periodic table is a tabular display of elements organized by their atomic numbers, electron configurations, and chemical properties.

Learning Objectives

Explain how properties of elements vary within groups and across periods in the periodic table

Key Takeaways

Key Points

• A periodic table is a useful framework for analyzing chemical behavior. Such tables are widely used in chemistry and other sciences.
• A group, or family, is a vertical column in the periodic table. Groups usually have more significant periodic trends than do periods and blocks.
• A period is a horizontal row in the periodic table. Elements in the same period show trends in atomic radius, ionization energy, electron affinity, and electronegativity.

Key Terms

• atomic orbital: The quantum mechanical behavior of an electron in an atom describing the probability of the electron’s particular position and energy.
• electron affinity: the amount of energy released when an electron is added to a neutral atom or molecule to form a negative ion
• ionization energy: the amount of energy required to remove an electron from an atom or molecule in the gas phase

The periodic table is a tabular display of the chemical elements. The elements are organized based on their atomic numbers, electron configurations, and recurring chemical properties.
In the periodic table, elements are presented in order of increasing atomic number (the number of protons). The rows of the table are called periods; the columns of the s- (columns 1-2 and He), d- (columns 3-12), and p-blocks (columns 13-18, except He) are called groups. (The terminology of s-, p-, and d- blocks originate from the valence atomic orbitals the element’s electrons occupy. ) Some groups have specific names, such as the halogens or the noble gases. Since, by definition, a periodic table incorporates recurring trends, any such table can be used to derive relationships between the properties of the elements and predict the properties of new, yet-to-be-discovered, or synthesized elements. As a result, the periodic table provides a useful framework for analyzing chemical behavior, and such tables are widely used in chemistry and other sciences.

Blocks in the Periodic Table: A diagram of the periodic table, highlighting the different blocks

History of the Periodic Table

Although precursors exist, Dmitri Mendeleev is generally credited with the publication, in 1869, of the first widely recognized periodic table. Mendeleev designed the table in such a way that recurring (“periodic”) trends in the properties of the elements could be shown. Using the trends he observed, he even left gaps for those elements that he thought were “missing. ” He even predicted the properties that he thought the missing elements would have when they were discovered. Many of these elements were indeed later discovered, and Mendeleev’s predictions were proved to be correct.

Groups

Agroup, or family, is a vertical column in the periodic table. Groups usually have more significant periodic trends than do periods and blocks, which are explained below. Modern quantum mechanical theories of atomic structure explain group trends by proposing that elements in the same group generally have the same electron configurations in their valence (or outermost, partially filled) shell. Consequently, elements in the same group tend to have shared chemistry and exhibit a clear trend in properties with increasing atomic number. However, in some parts of the periodic table, such as the d-block and the f-block, horizontal similarities can be as important as, or more pronounced than, vertical similarities.

Periods

A period is a horizontal row in the periodic table. Although groups generally have more significant periodic trends, there are regions where horizontal trends are more significant than vertical group trends, such as in the f-block, where the lanthanides and actinides form two substantial horizontal series of elements. Elements in the same period show trends in atomic radius, ionization energy, and electron affinity. Atomic radius usually decreases from left to right across a period. This occurs because each successive element has an added proton and electron, which causes the electron to be drawn closer to the nucleus, decreasing the radius.

The periodic table: Here is the complete periodic table with atomic numbers, groups, and periods. Each entry on the periodic table represents one element, and compounds are made up of several of these elements.

X-Rays

X-rays are a form of electromagnetic radiation and have wavelengths in the range of 0.01 to 10 nanometers.

Learning Objectives

Describe the properties of X-rays and how can be generated

Key Takeaways

Key Points

• X-rays can be generated by an x-ray tube, a vacuum tube, or a particle accelerator.
• X-ray fluorescence and Bremsstrahlung are processes through which x-rays are produced.
• Synchrotron radiation is generated by particle accelerators. Its unique features are x-ray outputs many orders of magnitude greater than those of x-ray tubes, wide x-ray spectra, excellent collimation, and linear polarization.

Key Terms

• photon: The quantum of light and other electromagnetic energy, regarded as a discrete particle having zero rest mass, no electric charge, and an indefinitely long lifetime.
• particle accelerator: A device that accelerates electrically charged particles to extremely high speeds, for the purpose of inducing high-energy reactions or producing high-energy radiation.

X-radiation (composed of x-rays) is a form of electromagnetic radiation. X-rays have wavelengths in the range of 0.01 to 10 nanometers, which corresponds to frequencies in the range of 30 petahertz to 30 exahertz (3·10¹⁶ Hz to 3·10¹⁹ Hz) and energies in the of range 100 eV to 100 keV.

X-Ray Spectrum and Applications: X-rays are part of the electromagnetic spectrum, with wavelengths shorter than those of visible light. Different applications use different parts of the X-ray spectrum.

X-rays can be generated by an x-ray tube, a vacuum tube that uses high voltage to accelerate the electrons released by a hot cathode to a high velocity. The high-velocity electrons collide with a metal target, the anode, creating the x-rays. The maximum energy of the produced x-ray photon is limited by the energy of the incident electron, which is equal to the voltage on the tube times the electron charge, so an 80-kV tube cannot create x-rays with an energy greater than 80 keV. When the electrons hit the target, x-rays are created through two different atomic processes:

1. X-ray fluorescence, if the electron has enough energy that it can knock an orbital electron out of the inner electron shell of a metal atom. As a result, electrons from higher energy levels fill up the vacancy, and x-ray photons are emitted. This process produces an emission spectrum of x-rays at a few discrete frequencies, sometimes referred to as the spectral lines. The spectral lines generated depend on the target (anode) element used and therefore are called characteristic lines. Usually these are transitions from upper shells into the K shell (called K lines), or the L shell (called L lines), and so on.
2. Bremsstrahlung, literally meaning braking radiation. Bremsstrahlung is radiation given off by the electrons as they are scattered by the strong electric field near the high-Z (proton number) nuclei. These x-rays have a continuous spectrum. The intensity of the x-rays increases linearly with decreasing frequency, from zero at the energy of the incident electrons, the voltage on the x-ray tube.

Both of these x-ray production processes are inefficient, with a production efficiency of only about one percent. Therefore, to produce a usable flux of x-rays, most of the electric power consumed by the tube is released as heat waste. The x-ray tube must be designed to dissipate this excess heat.
A specialized source of x-rays that is becoming widely used in research is synchrotron radiation, which is generated by particle accelerators. Its unique features are x-ray outputs many orders of magnitude greater than those of x-ray tubes, wide x-ray spectra, excellent collimation, and linear polarization.

Quantum-Mechanical View of Atoms

Atom is a basic unit of matter that consists of a nucleus surrounded by negatively charged electron cloud, commonly called atomic orbitals.

Learning Objectives

Identify major contributions to the understanding of atomic structure that were made by Niels Bohr, Erwin Schrödinger, and Werner Heisenberg

Key Takeaways

Key Points

• Niels Bohr suggested that the electrons were confined into clearly defined, quantized orbits, and could jump between these, but could not freely spiral inward or outward in intermediate states.
• Erwin Schrödinger, in 1926, developed a mathematical model of the atom that described the electrons as three-dimensional waveforms rather than point particles.
• Modern quantum mechanical view of hydrogen has evolved further after Schrödinger, by taking relativistic correction terms into account. This is referred to a quantum electrodynamics (QED).

Key Terms

• wave-particle duality: A postulation that all particles exhibit both wave and particle properties. It is a central concept of quantum mechanics.
• scanning tunneling microscope: An instrument for imaging surfaces at the atomic level.
• semiclassical approach: A theory in which one part of a system is described quantum-mechanically whereas the other is treated classically.

The atom is a basic unit of matter that consists of a nucleus surrounded by negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons. The electrons of an atom are bound to the nucleus by the electromagnetic (Coulomb) force. Atoms are minuscule objects with diameters of a few tenths of a nanometer and tiny masses proportional to the volume implied by these dimensions. Atoms in solid states (or, to be precise, their electron clouds) can be observed individually using special instruments such as the scanning tunneling microscope.

Hydrogen-1 (one proton + one electron) is the simplest form of atoms, and not surprisingly, our quantum mechanical understanding of atoms evolved with the understanding of this species. In 1913, physicist Niels Bohr suggested that the electrons were confined into clearly defined, quantized orbits, and could jump between these, but could not freely spiral inward or outward in intermediate states. An electron must absorb or emit specific amounts of energy to transition between these fixed orbits. Bohr’s model successfully explained spectroscopic data of hydrogen very well, but it adopted a semiclassical approach where electron was still considered a (classical) particle.

Adopting Louis de Broglie’s proposal of wave-particle duality, Erwin Schrödinger, in 1926, developed a mathematical model of the atom that described the electrons as three-dimensional waveforms rather than point particles. A consequence of using waveforms to describe particles is that it is mathematically impossible to obtain precise values for both the position and momentum of a particle at the same time; this became known as the uncertainty principle, formulated by Werner Heisenberg in 1926. Thereafter, the planetary model of the atom was discarded in favor of one that described atomic orbital zones around the nucleus where a given electron is most likely to be observed.

Illustration of the Helium Atom: This is an illustration of the helium atom, depicting the nucleus (pink) and the electron cloud distribution (black). The nucleus (upper right) in helium-4 is in reality spherically symmetric and closely resembles the electron cloud, although for more complicated nuclei this is not always the case. The black bar is one angstrom (10-10 m, or 100 pm).

Modern quantum mechanical view of hydrogen has evolved further after Schrödinger, by taking relativistic correction terms into account. Quantum electrodynamics (QED), a relativistic quantum field theory describing the interaction of electrically charged particles, has successfully predicted minuscule corrections in energy levels. One of the hydrogen’s atomic transitions (n=2 to n=1, n: principal quantum number) has been measured to an extraordinary precision of 1 part in a hundred trillion. This kind of spectroscopic precision allows physicists to refine quantum theories of atoms, by accounting for minuscule discrepancies between experimental results and theories. 

 

 

 

 

 

Planck’s Quantum Hypothesis and Black Body Radiation

A black body emits radiation called black body radiation. Planck described the radiation by assuming that radiation was emitted in quanta.

Learning Objectives

Identify assumption made by Max Planck to describe the electromagnetic radiation emitted by a black body

Key Takeaways

Key Points

• A black body in thermal equilibrium emits electromagnetic radiation called black body radiation.
• The radiation has a specific spectrum and intensity that depends only on the temperature of the body.
• Max Planck, in 1901, accurately described the radiation by assuming that electromagnetic radiation was emitted in discrete packets (or quanta). Planck’s quantum hypothesis is a pioneering work, heralding advent of a new era of modern physics and quantum theory.

Key Terms

• spectral radiance: measures of the quantity of radiation that passes through or is emitted from a surface and falls within a given solid angle in a specified direction.
• black body: An idealized physical body that absorbs all incident electromagnetic radiation, regardless of frequency or angle of incidence. Although black body is a theoretical concept, you can find approximate realizations of black body in nature.
• Planck constant: a physical constant that is the quantum of action in quantum mechanics. It has a unit of angular momentum. The Planck constant was first described as the proportionality constant between the energy of a photon (unit of electromagnetic radiation) and the frequency of its associated electromagnetic wave in his derivation of the Planck’s law

A black body in thermal equilibrium (i.e. at a constant temperature) emits electromagnetic radiation called black body radiation. Black body radiation has a characteristic, continuous frequency spectrum that depends only on the body’s temperature. Max Planck, in 1901, accurately described the radiation by assuming that electromagnetic radiation was emitted in discrete packets (or quanta). Planck’s quantum hypothesis is a pioneering work, heralding advent of a new era of modern physics and quantum theory.

Explaining the properties of black-body radiation was a major challenge in theoretical physics during the late nineteenth century. Predictions based on classical theories failed to explain black body spectra observed experimentally, especially at shorter wavelength. The puzzle was solved in 1901 by Max Planck in the formalism now known as Planck’s law of black-body radiation. Contrary to the common belief that electromagnetic radiation can take continuous values of energy, Planck introduced a radical concept that electromagnetic radiation was emitted in discrete packets (or quanta) of energy. Although Planck’s derivation is beyond the scope of this section (it will be covered in Quantum Mechanics), Planck’s law may be written:

${\text{B}}_{\lambda }\left(\text{T}\right)=\frac{2{\text{hc}}^2}{{\lambda }^5}\frac{1}{{\text{e}}^{\frac{\text{hc}}{\lambda {\text{k}}_{\text{B}}\text{T}}}-1}$

where $\text{B}$ is the spectral radiance of the surface of the black body, $\text{T}$ is its absolute temperature, $\lambda$ is wavelength of the radiation, ${\text{k}}_{\text{B}}$ is the Boltzmann constant, $\text{h}$ is the Planck constant, and $\text{c}$ is the speed of light. This equation explains the black body spectra shown below. Planck’s quantum hypothesis is one of the breakthroughs in the modern physics. It is not a surprise that he introduced Planck constant $\text{h}=6.626\times {10}^{-34}\text{J}\cdot \text{s}$  for the first time in his derivation of the Planck’s law.

Black body radiation spectrum: Typical spectrum from a black body at different temperatures (shown in blue, green and red curves). As the temperature decreases, the peak of the black-body radiation curve moves to lower intensities and longer wavelengths. Black line is a prediction of a classical theory for an object at 5,000K, showing catastropic discrepancy at shorter wavelengh.

Note that the spectral radiance depends on two variables, wavelength and temperature. The radiation has a specific spectrum and intensity that depends only on the temperature of the body. Despite its simplicity, Planck’s law describes radiation properties of objects (e.g. our body, planets, stars) reasonably well.

 

 

 

The Early Atom

The Discovery of the Parts of the Atom

Modern scientific usage denotes the atom as composed of constituent particles: the electron, the proton and the neutron.

Learning Objectives

Discuss experiments that led to discovery of the electron and the nucleus

Key Takeaways

Key Points

• The British physicist J. J. Thomson performed experiments studying cathode rays and discovered that they were unique particles, later named electrons.
• Rutherford proved that the hydrogen nucleus is present in other nuclei.
• In 1932, James Chadwick showed that there were uncharged particles in the radiation he was using. These particles, later called neutrons, had a similar mass of the protons but did not have the same characteristics as protons.

Key Terms

• scintillation: A flash of light produced in a transparent material by the passage of a particle.
• alpha particle: A positively charged nucleus of a helium-4 atom (consisting of two protons and two neutrons), emitted as a consequence of radioactivity.
• cathode: An electrode through which electric current flows out of a polarized electrical device.

Though originally viewed as a particle that cannot be cut into smaller particles, modern scientific usage denotes the atom as composed of various subatomic particles. The constituent particles of an atom (each discovered independently) are: the electron, the proton and the neutron. (The hydrogen-1 atom, however, has no neutrons, and a positive hydrogen ion has no electrons. )

Classical Atomic Model: Atomic model before the advent of Quantum Mechanics.

Electron

The German physicist Johann Wilhelm Hittorf undertook the study of electrical conductivity in rarefied gases. In 1869, he discovered a glow emitted from the cathode that increased in size with decrease in gas pressure. In 1896, the British physicist J. J. Thomson performed experiments demonstrating that cathode rays were unique particles, rather than waves, atoms or molecules, as was believed earlier. Thomson made good estimates of both the charge $\text{e}$ and the mass $\text{m}$ , finding that cathode ray particles (which he called “corpuscles”) had perhaps one thousandth the mass of hydrogen, the least massive ion known. He showed that their charge to mass ratio (e/m) was independent of cathode material. (Fig 1 shows a beam of deflected electrons. )

Electron Beam: A beam of electrons deflected in a circle by a magnetic field.

Proton

In 1917 (in experiments reported in 1919), Rutherford proved that the hydrogen nucleus is present in other nuclei, a result usually described as the discovery of the proton. Earlier, Rutherford learned to create hydrogen nuclei as a type of radiation produced as a yield of the impact of alpha particles on hydrogen gas; these nuclei were recognized by their unique penetration signature in air and their appearance in scintillation detectors. These experiments began when Rutherford noticed that when alpha particles were shot into air (mostly nitrogen), his scintillation detectors displayed the signatures of typical hydrogen nuclei as a product. After experimentation Rutherford traced the reaction to the nitrogen in air, and found that the effect was larger when alphas were produced into pure nitrogen gas. Rutherford determined that the only possible source of this hydrogen was the nitrogen, and therefore nitrogen must contain hydrogen nuclei. One hydrogen nucleus was knocked off by the impact of the alpha particle, producing oxygen-17 in the process. This was the first reported nuclear reaction, $14\text{N}+\alpha \to 17\text{O}+\text{p}$ .

Neutron

In 1920, Ernest Rutherford conceived the possible existence of the neutron. In particular, Rutherford examined the disparity found between the atomic number of an atom and its atomic mass. His explanation for this was the existence of a neutrally charged particle within the atomic nucleus. He considered the neutron to be a neutral double consisting of an electron orbiting a proton. In 1932, James Chadwick showed uncharged particles in the radiation he used. These particles had a similar mass as protons, but did not have the same characteristics as protons. Chadwick followed some of the predictions of Rutherford, the first to work in this then unknown field.

Early Models of the Atom

Dalton believed that that matter is composed of discrete units called atoms — indivisible, ultimate particles of matter.

Learning Objectives

Describe postulates of Dalton’s atomic theory and the atomic theories of ancient Greek philosophers

Key Takeaways

Key Points

• The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons.
• Scattered knowledge discovered by alchemists over the Middle Ages contributed to the discovery of atoms.
• Dalton established his atomic theory based on the fact that the masses of reactants in specific chemical reactions always have a particular mass ratio.

Key Terms

• electromagnetic force: a long-range fundamental force that acts between charged bodies, mediated by the exchange of photons
• Avogadro’s number: the number of constituent particles (usually atoms or molecules) in one mole of a given substance. It has dimensions of reciprocal mol and its value is equal to $6.02214129 \cdot 10^{23} \text{ mol}^{-1}$
• nucleus: the massive, positively charged central part of an atom, made up of protons and neutrons

The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons (except in the case of hydrogen-1, which is the only stable nuclide with no neutrons). The electrons of an atom are bound to the nucleus by the electromagnetic force. We have a detailed (and accurate) model of the atom now, but it took a long time to come up with the correct answer.

Illustration of the Helium Atom: This is an illustration of the helium atom, depicting the nucleus (pink) and the electron cloud distribution (black). The nucleus (upper right) in helium-4 is in reality spherically symmetric and closely resembles the electron cloud, although for more complicated nuclei this is not always the case. The black bar is one angstrom (${10}^{-10}$ m, or 100 pm).

People have long speculated about the structure of matter and the existence of atoms. The earliest significant ideas to survive are from the ancient Greeks in the fifth century BC, especially from the philosophers Leucippus and Democritus. (There is some evidence that philosophers in both India and China made similar speculations at about the same time. ) They considered the question of whether a substance can be divided without limit into ever smaller pieces. There are only a few possible answers to this question. One is that infinitesimally small subdivision is possible. Another is what Democritus in particular believed — that there is a smallest unit that cannot be further subdivided. Democritus called this the atom. We now know that atoms themselves can be subdivided, but their identity is destroyed in the process, so the Greeks were correct in a respect. The Greeks also felt that atoms were in constant motion, another correct notion.
The Greeks and others speculated about the properties of atoms, proposing that only a few types existed and that all matter was formed as various combinations of these types. The famous proposal that the basic elements were earth, air, fire, and water was brilliant but incorrect. The Greeks had identified the most common examples of the four states of matter (solid, gas, plasma, and liquid) rather than the basic chemical elements. More than 2000 years passed before observations could be made with equipment capable of revealing the true nature of atoms.
Over the centuries, discoveries were made regarding the properties of substances and their chemical reactions. Certain systematic features were recognized, but similarities between common and rare elements resulted in efforts to transmute them (lead into gold, in particular) for financial gain. Secrecy was commonplace. Alchemists discovered and rediscovered many facts but did not make them broadly available. As the Middle Ages ended, the practice of alchemy gradually faded, and the science of chemistry arose. It was no longer possible, nor considered desirable, to keep discoveries secret. Collective knowledge grew, and by the beginning of the 19^th century, an important fact was well established: the masses of reactants in specific chemical reactions always have a particular mass ratio. This is very strong indirect evidence that there are basic units (atoms and molecules) that have these same mass ratios. English chemist John Dalton (1766-1844) did much of this work, with significant contributions by the Italian physicist Amedeo Avogadro (1776-1856). It was Avogadro who developed the idea of a fixed number of atoms and molecules in a mole. This special number is called Avogadro’s number in his honor ($6.022\cdot {10}^{23}$ ).
Dalton believed that matter is composed of discrete units called atoms, as opposed to the obsolete notion that matter could be divided into any arbitrarily small quantity. He also believed that atoms are the indivisible, ultimate particles of matter. However, this belief was overturned near the end of the 19^th century by Thomson, with his discovery of electrons.

Intro to the History of Atomic Theory – Intro: Rutherford, Thomson, electrons, nuclei, and plums. I don’t mean to be a bohr, but do you think pudding should have a role in serious scientific inquiry?

The Thomson Model

Thomson proposed that the atom is composed of electrons surrounded by a soup of positive charge to balance the electrons’ negative charges.

Learning Objectives

Describe model of an atom proposed by J. J. Thomson.

Key Takeaways

Key Points

• J. J. Thomson, who discovered the electron in 1897, proposed the plum pudding model of the atom in 1904 before the discovery of the atomic nucleus in order to include the electron in the atomic model.
• In Thomson’s model, the atom is composed of electrons surrounded by a soup of positive charge to balance the electrons’ negative charges, like negatively charged “plums” surrounded by positively charged “pudding”.
• The 1904 Thomson model was disproved by Hans Geiger’s and Ernest Marsden’s 1909 gold foil experiment.

Key Terms

• nucleus: the massive, positively charged central part of an atom, made up of protons and neutrons

J. J. Thomson, who discovered the electron in 1897, proposed the plum pudding model of the atom in 1904 before the discovery of the atomic nucleus in order to include the electron in the atomic model. In Thomson’s model, the atom is composed of electrons (which Thomson still called “corpuscles,” though G. J. Stoney had proposed that atoms of electricity be called electrons in 1894) surrounded by a soup of positive charge to balance the electrons’ negative charges, like negatively charged “plums” surrounded by positively charged “pudding”. The electrons (as we know them today) were thought to be positioned throughout the atom in rotating rings. In this model the atom was also sometimes described to have a “cloud” of positive charge.

Plum pudding model of the atom: A schematic presentation of the plum pudding model of the atom; in Thomson’s mathematical model the “corpuscles” (in modern language, electrons) were arranged non-randomly, in rotating rings.

With this model, Thomson abandoned his earlier “nebular atom” hypothesis, in which the atom was composed of immaterial vortices. Now, at least part of the atom was to be composed of Thomson’s particulate negative corpuscles, although the rest of the positively charged part of the atom remained somewhat nebulous and ill-defined.
The 1904 Thomson model was disproved by the 1909 gold foil experiment performed by Hans Geiger and Ernest Marsden. This gold foil experiment was interpreted by Ernest Rutherford in 1911 to suggest that there is a very small nucleus of the atom that contains a very high positive charge (in the case of gold, enough to balance the collective negative charge of about 100 electrons). His conclusions led him to propose the Rutherford model of the atom.

Intro to the History of Atomic Theory – The Thomson Model: Rutherford, Thomson, electrons, nuclei, and plums. I don’t mean to be a bohr, but do you think pudding should have a role in serious scientific inquiry?

The Rutherford Model

Rutherford confirmed that the atom had a concentrated center of positive charge and relatively large mass.

Learning Objectives

Describe gold foil experiment performed by Geiger and Marsden under directions of Rutherford and its implications for the model of the atom

Key Takeaways

Key Points

• Rutherford overturned Thomson’s model in 1911 with his well-known gold foil experiment, in which he demonstrated that the atom has a tiny, high- mass nucleus.
• In his experiment, Rutherford observed that many alpha particles were deflected at small angles while others were reflected back to the alpha source.
• This highly concentrated, positively charged region is named the “nucleus” of the atom.

Key Terms

• alpha particle: A positively charged nucleus of a helium-4 atom (consisting of two protons and two neutrons), emitted as a consequence of radioactivity; α-particle.

The Rutherford model is a model of the atom named after Ernest Rutherford. Rutherford directed the famous Geiger-Marsden experiment in 1909, which suggested, according to Rutherford’s 1911 analysis, that J. J. Thomson’s so-called “plum pudding model” of the atom was incorrect. Rutherford’s new model for the atom, based on the experimental results, contained the new features of a relatively high central charge concentrated into a very small volume in comparison to the rest of the atom. This central volume also contained the bulk of the atom’s mass. This region would later be named the “nucleus. ”

Atomic Planetary Model: Basic diagram of the atomic planetary model; electrons are in green, and the nucleus is in red

In 1911, Rutherford designed an experiment to further explore atomic structure using the alpha particles emitted by a radioactive element. Following his direction, Geiger and Marsden shot alpha particles with large kinetic energies toward a thin foil of gold. Measuring the pattern of scattered particles was expected to provide information about the distribution of charge within the atom. Under the prevailing plum pudding model, the alpha particles should all have been deflected by, at most, a few degrees. However, the actual results surprised Rutherford. Although many of the alpha particles did pass through as expected, many others were deflected at small angles while others were reflected back to the alpha source.

From purely energetic considerations of how far particles of known speed would be able to penetrate toward a central charge of 100 e, Rutherford was able to calculate that the radius of his gold central charge would need to be less than $3.4\cdot {10}^{-14}$ meters. This was in a gold atom known to be about ${10}^{-10}$ meters in radius; a very surprising finding, as it implied a strong central charge less than $\frac{1}{3000}$ ^th of the diameter of the atom.

Intro to the History of Atomic Theory – The Rutherford Model: Rutherford, Thomson, electrons, nuclei, and plums. I don’t mean to be a bohr, but do you think pudding should have a role in serious scientific inquiry?

The Bohr Model of the Atom

Bohr suggested that electrons in hydrogen could have certain classical motions only when restricted by a quantum rule.

Learning Objectives

Describe model of atom proposed by Niels Bohr.

Key Takeaways

Key Points

• According to Bohr: 1) Electrons in atoms orbit the nucleus, 2) The electrons can only orbit stably, without radiating, in certain orbits, and 3) Electrons can only gain and lose energy by jumping from one allowed orbit to another.
• The significance of the Bohr model is that the laws of classical mechanics apply to the motion of the electron about the nucleus only when restricted by a quantum rule. Therefore, his atomic model is called a semiclassical model.
• The laws of classical mechanics predict that the electron should release electromagnetic radiation while orbiting a nucleus, suggesting that all atoms should be unstable!

Key Terms

• Maxwell’s equations: A set of equations describing how electric and magnetic fields are generated and altered by each other and by charges and currents.
• semiclassical: a theory in which one part of a system is described quantum-mechanically whereas the other is treated classically.

The Bohr Model of the Atom

The great Danish physicist Niels Bohr (1885–1962, ) made immediate use of Rutherford’s planetary model of the atom. Bohr became convinced of its validity and spent part of 1912 at Rutherford’s laboratory. In 1913, after returning to Copenhagen, he began publishing his theory of the simplest atom, hydrogen, based on the planetary model of the atom.

Niels Bohr: Niels Bohr, Danish physicist, used the planetary model of the atom to explain the atomic spectrum and size of the hydrogen atom. His many contributions to the development of atomic physics and quantum mechanics; his personal influence on many students and colleagues; and his personal integrity, especially in the face of Nazi oppression, earned him a prominent place in history. (credit: Unknown Author, via Wikimedia Commons)

For decades, many questions had been asked about atomic characteristics. From their sizes to their spectra, much was known about atoms, but little had been explained in terms of the laws of physics. Bohr’s theory explained the atomic spectrum of hydrogen, made him instantly famous, and established new and broadly applicable principles in quantum mechanics.
One big puzzle that the planetary-model of atom had was the following. The laws of classical mechanics predict that the electron should release electromagnetic radiation while orbiting a nucleus (according to Maxwell’s equations, accelerating charge should emit electromagnetic radiation). Because the electron would lose energy, it would gradually spiral inwards, collapsing into the nucleus. This atom model is disastrous, because it predicts that all atoms are unstable. Also, as the electron spirals inward, the emission would gradually increase in frequency as the orbit got smaller and faster. This would produce a continuous smear, in frequency, of electromagnetic radiation. However, late 19th century experiments with electric discharges have shown that atoms will only emit light (that is, electromagnetic radiation) at certain discrete frequencies.
To overcome this difficulty, Niels Bohr proposed, in 1913, what is now called the Bohr model of the atom. He suggested that electrons could only have certain classical motions:

1. Electrons in atoms orbit the nucleus.
2. The electrons can only orbit stably, without radiating, in certain orbits (called by Bohr the “stationary orbits”): at a certain discrete set of distances from the nucleus. These orbits are associated with definite energies and are also called energy shells or energy levels. In these orbits, the electron’s acceleration does not result in radiation and energy loss as required by classical electrodynamics.
3. Electrons can only gain and lose energy by jumping from one allowed orbit to another, absorbing or emitting electromagnetic radiation with a frequency $\nu$ determined by the energy difference of the levels according to the Planck relation:

$\Delta \text{E}={\text{E}}_2-{\text{E}}_1=\text{h}\nu$
where $\text{h}$ is Planck’s constant and $\nu$ is the frequency of the radiation.

Semiclassical Model

The significance of the Bohr model is that the laws of classical mechanics apply to the motion of the electron about the nucleus only when restricted by a quantum rule. Therefore, his atomic model is called a semiclassical model.

Basic Assumptions of the Bohr Model

Bohr explained hydrogen’s spectrum successfully by adopting a quantization condition and by introducing the Planck constant in his model.

Learning Objectives

Describe basic assumptions that were applied by Niels Bohr to the planetary model of an atom

Key Takeaways

Key Points

• Classical electrodynamics predicts that an atom described by a (classical) planetary model would be unstable.
• To explain the hydrogen spectrum, Bohr had to make a few assumptions that electrons could only have certain classical motions.
• After the seminal work by Planck, Einstein, and Bohr, physicists began to realize that it was essential to introduce the notion of ” quantization ” to explain microscopic worlds.

Key Terms

• black body: An idealized physical body that absorbs all incident electromagnetic radiation, regardless of frequency or angle of incidence. Although black body is a theoretical concept, you can find approximate realizations of black body in nature.
• photoelectric effect: The occurrence of electrons being emitted from matter (metals and non-metallic solids, liquids, or gases) as a consequence of their absorption of energy from electromagnetic radiation.

In previous modules, we have seen puzzles from classical atomic theories (e.g., the Rutherford model). Most importantly, classical electrodynamics predicts that an atom described by a (classical) planetary model would be unstable. To explain the puzzle, Bohr proposed what is now called the Bohr model of the atom in 1913. He suggested that electrons could only have certain classical motions:

1. Electrons in atoms orbit the nucleus.
2. The electrons can only orbit stably, without radiating, in certain orbits (called by Bohr the “stationary orbits”) at a certain discrete set of distances from the nucleus. These orbits are associated with definite energies and are also called energy shells or energy levels. In these orbits, the electron’s acceleration does not result in radiation and energy loss as required by classical electrodynamics.
3. Electrons can only gain and lose energy by jumping from one allowed orbit to another, absorbing or emitting electromagnetic radiation with a frequency $\nu$ determined by the energy difference of the levels according to the Planck relation: $\Delta \text{E}={\text{E}}_2-{\text{E}}_1=\text{h}\nu$ , where $\text{h}$ is the Planck constant. In addition, Bohr also assumed that the angular momentum $\text{L}$ is restricted to be an integer multiple of a fixed unit: $\text{L}=\text{n}\frac{\text{h}}{2\pi }=\text{n}\hslash$ , where $\text{n}=1,2,3,\dots$ is called the principal quantum number, and $\hslash =\frac{\text{h}}{2\pi }$ .

We have seen that Planck adopted a new condition of energy quantization to explain the black body radiation, where he introduced the Planck constant $\text{h}$ for the first time. Soon after, Einstein resorted to this new concept of energy quantization and used the Planck constant again to explain the photoelectric effects, in which he assumed that electromagnetic radiation interact with matter as particles (later named “photons”). Here, Bohr explained the atomic hydrogen spectrum successfully for the first time by adopting a quantization condition and by introducing the Planck constant in his atomic model. Over the period of radical development in the early 20^th century, physicists began to realize that it was essential to introduce the notion of “quantization” to explain microscopic worlds.

Rutherford-Bohr model: The Rutherford–Bohr model of the hydrogen atom ($\text{Z}=1$ ) or a hydrogen-like ion ($\text{Z}>1$ ), where the negatively charged electron confined to an atomic shell encircles a small, positively charged atomic nucleus, and where an electron jump between orbits is accompanied by an emitted or absorbed amount of electromagnetic energy ($\text{h}\nu$ ). The orbits in which the electron may travel are shown as gray circles; their radius increases as ${\text{n}}^2$ , where $\text{n}$ is the principal quantum number. The $3\to 2$ transition depicted here produces the first line of the Balmer series, and for hydrogen ($\text{Z}=1$ ) it results in a photon of wavelength 656 nm (red light).

Bohr Orbits

According to Bohr, electrons can only orbit stably, in certain orbits, at a certain discrete set of distances from the nucleus.

Learning Objectives

Explain relationship between the “Bohr orbits” and the quantization effect

Key Takeaways

Key Points

• The “Bohr orbits” have a very important feature of quantization: that the angular momentum L of an electron in its orbit is quantized, that is, it has only specific, discrete values. This leads to the equation L=mevrn=nℏL = m_e v r_n = n\hbar.
• At the time of proposal, Bohr himself did not know why angular momentum should be quantized, but using this assumption he was able to calculate the energies in the hydrogen spectrum.
• A theory of the atom or any other system must predict its energies based on the physics of the system, which the Bohr model was able to do.

Key Terms

• quantization: The process of explaining a classical understanding of physical phenomena in terms of a newer understanding known as quantum mechanics.

Danish Physicist Neils Bohr was clever enough to discover a method of calculating the electron orbital energies in hydrogen. As we’ve seen in the previous module “The Bohr Model of Atom,” Bohr assumed that the electrons can only orbit stably, without radiating, in certain orbits (named by Bohr as “stationary orbits”), at a certain discrete set of distances from the nucleus. These “Bohr orbits” have a very important feature of quantization as shown in the following. This was an important first step that has been improved upon, but it is well worth repeating here, as it correctly describes many characteristics of hydrogen. Assuming circular orbits, Bohr proposed that the angular momentum $\text{L}$ of an electron in its orbit is quantized, that is, has only specific, discrete values. The value for $\text{L}$ is given by the formula:
$\text{L}={\text{m}}_{\text{e}}\text{v}{\text{r}}_{\text{n}}=\text{n}\frac{\text{h}}{2\pi }=\text{n}\hslash$
where $\text{L}$ is the angular momentum, ${\text{m}}_{\text{e}}$  is the electron’s mass, ${\text{r}}_{\text{n}}$  is the radius of the $\text{n}$ -th orbit, and $\text{h}$ is Planck’s constant. Note that angular momentum is $\text{L}=\text{I}\omega$ . For a small object at a radius $\text{r}$ , $\text{I}={\text{mr}}^2$  and $\omega =\frac{\text{v}}{\text{r}}$ , so that:
$\text{L}=\left({\text{mr}}^2\right)\left(\frac{\text{v}}{\text{r}}\right)=\text{mvr}$
Quantization says that this value of $\text{mvr}$ can only have discrete values. At the time, Bohr himself did not know why angular momentum should be quantized, but using this assumption he was able to calculate the energies in the hydrogen spectrum, something no one else had done at the time.
Below is an energy-level diagram, which is a convenient way to display energy states—the allowed energy levels of the electron (as relative to our discussion). Energy is plotted vertically with the lowest or ground state at the bottom and with excited states above. Given the energies of the lines in an atomic spectrum, it is possible (although sometimes very difficult) to determine the energy levels of an atom. Energy-level diagrams are used for many systems, including molecules and nuclei. A theory of the atom or any other system must predict its energies based on the physics of the system.

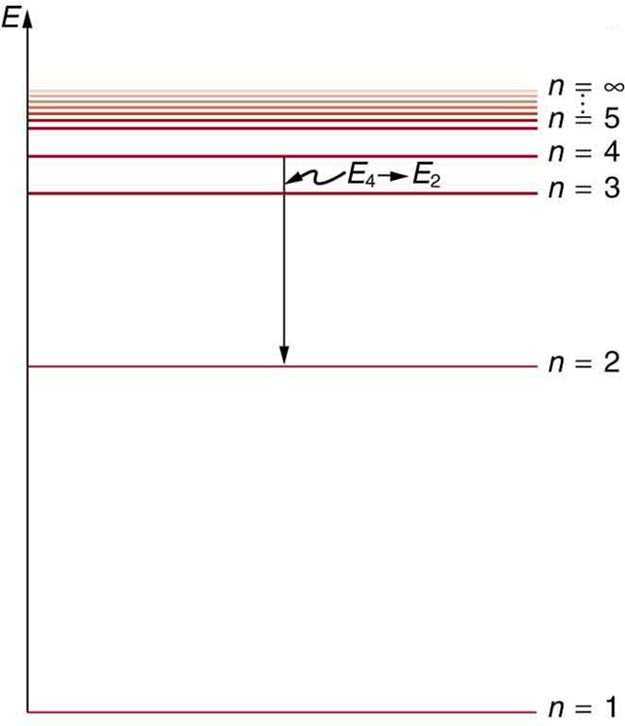
Energy-Level Diagram Plot: An energy-level diagram plots energy vertically and is useful in visualizing the energy states of a system and the transitions between them. This diagram is for the hydrogen-atom electrons, showing a transition between two orbits having energies ${\text{E}}_4$ and ${\text{E}}_2$ .

Energy of a Bohr Orbit

Based on his assumptions, Bohr derived several important properties of the hydrogen atom from the classical physics.

Learning Objectives

Apply proper equation to calculate energy levels and the energy of an emitted photon for a hydrogen-like atom

Key Takeaways

Key Points

• According to Bohr, allowed orbit radius at any $\text{n}$ is ${\text{r}}_{\text{n}}=\frac{{\text{n}}^2{\hslash }^2}{{\text{Zk}}_{\text{e}}{\text{e}}^2{\text{m}}_{\text{e}}}$ . The smallest possible value of $\text{r}$ in the hydrogen atom is called the Bohr radius and is equal to 0.053 nm.
• The energy of the $\text{n}$ -th level for any atom is $\text{E}=\approx \frac{-13.6{\text{Z}}^2}{{\text{n}}^2}\text{eV}$ .
• The energy of a photon emitted by a hydrogen atom is given by the difference of two hydrogen energy levels: $\text{E}={\text{E}}_{\text{i}}-{\text{E}}_{\text{f}}=\text{R}\left(\frac{1}{{\text{n}}_{\text{f}}^2}-\frac{1}{{\text{n}}_{\text{i}}^2}\right)$ , which is known as Rydberg formula.

Key Terms

• centripetal: Directed or moving towards a center.

From Bohr’s assumptions, we will now derive a number of important properties of the hydrogen atom from the classical physics. We start by noting the centripetal force causing the electron to follow a circular path is supplied by the Coulomb force. To be more general, we note that this analysis is valid for any single-electron atom. So, if a nucleus has $\text{Z}$ protons ($\text{Z}=1$ for hydrogen, $\text{Z}=2$ for helium, etc.) and only one electron, that atom is called a hydrogen-like atom.
The spectra of hydrogen-like ions are similar to hydrogen, but shifted to higher energy by the greater attractive force between the electron and nucleus. The magnitude of the centripetal force is $\frac{{\text{m}}_{\text{ev}}^2}{{\text{r}}_{\text{n}}}$ , while the Coulomb force is $\frac{{\text{Zk}}_{\text{e}}{\text{e}}^2}{{\text{r}}^2}$ . The tacit assumption here is that the nucleus is more massive than the stationary electron, and the electron orbits about it. This is consistent with the planetary model of the atom. Equating these:
$\frac{{\text{m}}_{\text{e}}{\text{v}}^2}{\text{r}}=\frac{{\text{Zk}}_{\text{e}}{\text{e}}^2}{{\text{r}}^2}$
This equation determines the electron’s speed at any radius:
$\text{v}=\frac{\sqrt{{\text{Zk}}_{\text{e}}{\text{e}}^2}}{{\text{m}}_{\text{e}}\text{r}}$
It also determines the electron’s total energy at any radius:
$\text{E}=\frac{1}{2}{\text{m}}_{\text{e}}{\text{v}}^2-\frac{\text{Z}{\text{k}}_{\text{e}}{\text{e}}^2}{\text{r}}=-\frac{\text{Z}{\text{k}}_{\text{e}}{\text{e}}^2}{2\text{r}}$
The total energy is negative and inversely proportional to $\text{r}$ . This means that it takes energy to pull the orbiting electron away from the proton. For infinite values of $\text{r}$ , the energy is zero, corresponding to a motionless electron infinitely far from the proton.
Now, here comes the Quantum rule: As we saw in the previous module, the angular momentum $\text{L}={\text{m}}_{\text{e}}\text{r}\text{v}$ is an integer multiple of $\hslash$ :
${\text{m}}_{\text{e}}\text{v}\text{r}=\text{n}\hslash$
Substituting the expression in the equation for speed above gives an equation for $\text{r}$ in terms of $\text{n}$ :
$\sqrt{{\text{Zk}}_{\text{e}}{\text{e}}^2{\text{m}}_{\text{e}}\text{r}}=\text{n}\hslash$
The allowed orbit radius at any n is then:
${\text{r}}_{\text{n}}=\frac{{\text{n}}^2{\hslash }^2}{{\text{Zk}}_{\text{e}}{\text{e}}^2{\text{m}}_{\text{e}}}$
The smallest possible value of $\text{r}$ in the hydrogen atom is called the Bohr radius and is equal to 0.053 nm. The energy of the $\text{n}$ -th level for any atom is determined by the radius and quantum number:
$\text{E}=-\frac{{\text{Zk}}_{\text{e}}{\text{e}}^2}{2{\text{r}}_{\text{n}}}=-\frac{{\text{Z}}^2({\text{k}}_{\text{e}}{\text{e}}^2{)}^2{\text{m}}_{\text{e}}}{2{\hslash }^2{\text{n}}^2}\approx \frac{-13.6{\text{Z}}^2}{{\text{n}}^2}\text{eV}$
Using this equation, the energy of a photon emitted by a hydrogen atom is given by the difference of two hydrogen energy levels:
$\text{E}={\text{E}}_{\text{i}}-{\text{E}}_{\text{f}}=\text{R}\left(\frac{1}{{\text{n}}_{\text{f}}^2}-\frac{1}{{\text{n}}_{\text{i}}^2}\right)$
Which is the Rydberg formula describing all the hydrogen spectrum and $\text{R}$  is the Rydberg constant. Bohr’s model predicted experimental hydrogen spectrum extremely well.

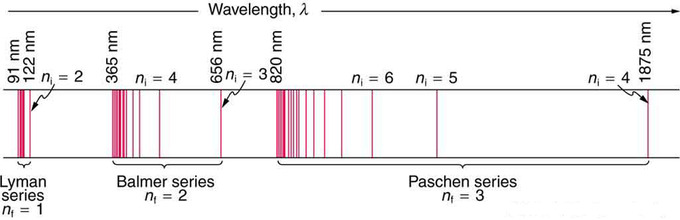
Fig 1: A schematic of the hydrogen spectrum shows several series named for those who contributed most to their determination. Part of the Balmer series is in the visible spectrum, while the Lyman series is entirely in the UV, and the Paschen series and others are in the IR. Values of nf and ni are shown for some of the lines.

Hydrogen Spectra

The observed hydrogen-spectrum wavelengths can be calculated using the following formula: $\frac{1}{\lambda }=\text{R}(\frac{1}{{\text{n}}_{\text{f}}^2}-\frac{1}{{\text{n}}_{\text{i}}^2})$ .

Learning Objectives

Explain difference between Lyman, Balmer, and Paschen series

Key Takeaways

Key Points

• Atomic and molecular emission and absorption spectra have been known for over a century to be discrete (or quantized).
• Lyman, Balmer, and Paschen series are named after early researchers who studied them in particular depth.
• Bohr was the first one to provide a theoretical explanation of the hydrogen spectra.

Key Terms

• photon: The quantum of light and other electromagnetic energy, regarded as a discrete particle having zero rest mass, no electric charge, and an indefinitely long lifetime.
• spectrum: A condition that is not limited to a specific set of values but can vary infinitely within a continuum. The word saw its first scientific use within the field of optics to describe the rainbow of colors in visible light when separated using a prism.

For decades, many questions had been asked about atomic characteristics. From their sizes to their spectra, much was known about atoms, but little had been explained in terms of the laws of physics. Atomic and molecular emission and absorption spectra have been known for over a century to be discrete (or quantized). Maxwell and others had realized that there must be a connection between the spectrum of an atom and its structure, something like the resonant frequencies of musical instruments. But, despite years of efforts by many great minds, no one had a workable theory. (It was a running joke that any theory of atomic and molecular spectra could be destroyed by throwing a book of data at it, so complex were the spectra.) Following Einstein’s proposal of photons with quantized energies directly proportional to their wavelengths, it became even more evident that electrons in atoms can exist only in discrete orbits.
In some cases, it had been possible to devise formulas that described the emission spectra. As you might expect, the simplest atom—hydrogen, with its single electron—has a relatively simple spectrum. The hydrogen spectrum had been observed in the infrared (IR), visible, and ultraviolet (UV), and several series of spectral lines had been observed. The observed hydrogen-spectrum wavelengths can be calculated using the following formula:
$\frac{1}{\lambda }=\text{R}(\frac{1}{{\text{n}}_{\text{f}}^2}-\frac{1}{{\text{n}}_{\text{i}}^2})$
where $\lambda$  is the wavelength of the emitted EM radiation and $\text{R}$ is the Rydberg constant, determined by the experiment to be $\text{R}=1.097\cdot {10}^7{\text{text{m}}}^{-1}$ , and ${\text{n}}_{\text{f}}$ , ${\text{n}}_{\text{i}}$ are positive integers associated with a specific series.
These series are named after early researchers who studied them in particular depth. For the Lyman series, ${\text{n}}_{\text{f}}=1$ for the Balmer series, ${\text{n}}_{\text{f}}=2$ ; for the Paschen series, ${\text{n}}_{\text{f}}=3$ ; and so on. The Lyman series is entirely in the UV, while part of the Balmer series is visible with the remainder UV. The Paschen series and all the rest are entirely IR. There are apparently an unlimited number of series, although they lie progressively farther into the infrared and become difficult to observe as ${\text{n}}_{\text{f}}$ increases. The constant ${\text{n}}_{\text{i}}$ is a positive integer, but it must be greater than ${\text{n}}_{\text{f}}$ . Thus, for the Balmer series, ${\text{n}}_{\text{f}}=2$ and ${\text{n}}_{\text{i}}=3,4,5,6\dots \left[/latex\right].Notethat\left[latex\right]{\text{n}}_{\text{i}}$ can approach infinity.

Electron transitions and their resulting wavelengths for hydrogen.: Energy levels are not to scale.

While the formula in the wavelengths equation was just a recipe designed to fit data and was not based on physical principles, it did imply a deeper meaning. Balmer first devised the formula for his series alone, and it was later found to describe all the other series by using different values of ${\text{n}}_{\text{f}}$ . Bohr was the first to comprehend the deeper meaning. Again, we see the interplay between experiment and theory in physics. Experimentally, the spectra were well established, an equation was found to fit the experimental data, but the theoretical foundation was missing.

de Broglie and the Bohr Model

By assuming that the electron is described by a wave and a whole number of wavelengths must fit, we derive Bohr’s quantization assumption.

Learning Objectives

Describe reinterpretation of Bohr’s condition by de Broglie

Key Takeaways

Key Points

• Bohr’s condition, that the angular momentum is an integer multiple of $\hslash$ , was later reinterpreted in 1924 by de Broglie as a standing wave condition.
• For what Bohr was forced to hypothesize as the rule for allowed orbits, de Broglie’s matter wave concept explains it as the condition for constructive interference of an electron in a circular orbit.
• Bohr’s model was only applicable to hydrogen-like atoms. In 1925, more general forms of description (now called quantum mechanics ) emerged, thanks to Heisenberg and Schrodinger.

Key Terms

• standing wave: A wave form which occurs in a limited, fixed medium in such a way that the reflected wave coincides with the produced wave. A common example is the vibration of the strings on a musical stringed instrument.
• matter wave: A concept reflects the wave-particle duality of matter. The theory was proposed by Louis de Broglie.

Bohr’s condition, that the angular momentum is an integer multiple of $\hslash$ , was later reinterpreted in 1924 by de Broglie as a standing wave condition. The wave-like properties of matter were subsequently confirmed by observations of electron interference when scattered from crystals. Electrons can exist only in locations where they interfere constructively. How does this affect electrons in atomic orbits? When an electron is bound to an atom, its wavelength must fit into a small space, something like a standing wave on a string.

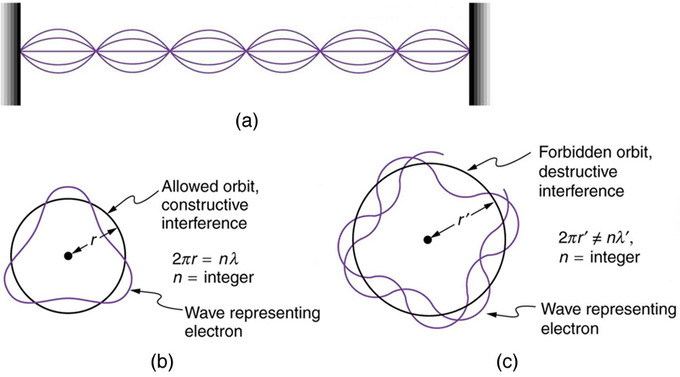
Waves on a String: (a) Waves on a string have a wavelength related to the length of the string, allowing them to interfere constructively. (b) If we imagine the string bent into a closed circle, we get a rough idea of how electrons in circular orbits can interfere constructively. (c) If the wavelength does not fit into the circumference, the electron interferes destructively; it cannot exist in such an orbit.

Allowed orbits are those in which an electron constructively interferes with itself. Not all orbits produce constructive interference and thus only certain orbits are allowed (i.e., the orbits are quantized). By assuming that the electron is described by a wave and a whole number of wavelengths must fit along the circumference of the electron’s orbit, we have the equation:
$\text{n}\lambda =2\pi \text{r}$
Substituting de Broglie’s wavelength of $\frac{\text{h}}{\text{p}}$ reproduces Bohr’s rule. Since $\lambda =\text{h}/{\text{m}}_{\text{ev}}$ , we now have:
$\frac{\text{nh}}{{\text{m}}_{\text{ev}}}=2\pi {\text{r}}_{\text{n}}$
Rearranging terms, and noting that $\text{L}=\text{mvr}$ for a circular orbit, we obtain the quantization of angular momentum as the condition for allowed orbits:
[latex]\displaystyle \text{L} = \text{m}_\text{e} \text{v} \text{r}_\text{n} = \text{n} \frac{\text{h}}{2\pi}, (\text{n}=1,2,3…)[/latex]
As previously stated, Bohr was forced to hypothesize this rule for allowed orbits. We now realize this as the condition for constructive interference of an electron in a circular orbit.
Accordingly, a new kind of mechanics, quantum mechanics, was proposed in 1925. Bohr’s model of electrons traveling in quantized orbits was extended into a more accurate model of electron motion. The new theory was proposed by Werner Heisenberg. By different reasoning, another form of the same theory, wave mechanics, was discovered independently by Austrian physicist Erwin Schrödinger. Schrödinger employed de Broglie’s matter waves, but instead sought wave solutions of a three-dimensional wave equation. This described electrons that were constrained to move about the nucleus of a hydrogen-like atom by being trapped by the potential of the positive nuclear charge.

de Broglie’s Matter Waves Justify Bohr’s Magic Electron Orbital Radii: I include a summary of the hydrogen atom’s electronic structure and explain how an electron can interfere with itself in an orbit just like it can in a double-slit experiment.

X-Rays and the Compton Effect

Compton explained the X-ray frequency shift during the X-ray/electron scattering by attributing particle-like momentum to “photons”.

Learning Objectives

Describe Compton effects between electrons and x-ray photons

Key Takeaways

Key Points

• Compton derived the mathematical relationship between the shift in wavelength and the scattering angle of the X-rays.
• Compton effects (with electrons) usually occur with x-ray photons.
• If the photon is of lower energy, in the visible light through soft X-rays range, photoelectric effects are observed. Higher energy photons, in the gamma ray range, may lead to pair production.

Key Terms

• gamma ray: A very high frequency (and therefore very high energy) electromagnetic radiation emitted as a consequence of radioactivity.
• photoelectric effects: In photoelectric effects, electrons are emitted from matter (metals and non-metallic solids, liquids or gases) as a consequence of their absorption of energy from electromagnetic radiation.
• photon: The quantum of light and other electromagnetic energy, regarded as a discrete particle having zero rest mass, no electric charge, and an indefinitely long lifetime.

By the early 20th century, research into the interaction of X-rays with matter was well underway. It was observed that when X-rays of a known wavelength interact with atoms, the X-rays are scattered through an angle $\theta$ and emerge at a different wavelength related to $\theta$ . Although classical electromagnetism predicted that the wavelength of scattered rays should be equal to the initial wavelength, multiple experiments had found that the wavelength of the scattered rays was longer (corresponding to lower energy) than the initial wavelength.
In 1923, Compton published a paper in the Physical Review which explained the X-ray shift by attributing particle-like momentum to “photons,” which Einstein had invoked in his Nobel prize winning explanation of the photoelectric effect. First postulated by Planck, these “particles” conceptualized “quantized” elements of light as containing a specific amount of energy depending only on the frequency of the light. In his paper, Compton derived the mathematical relationship between the shift in wavelength and the scattering angle of the X-rays by assuming that each scattered X-ray photon interacted with only one electron. His paper concludes by reporting on experiments which verified his derived relation:
${\lambda }^{\prime }-\lambda =\frac{\text{h}}{{\text{m}}_{\text{e}}\text{c}}(1-\cos \theta )$
where λ\lambda is the initial wavelength, λ′\lambda’ is the wavelength after scattering, $\text{h}$ is the Planck constant, mem_e is the Electron rest mass, $\text{c}$ is the speed of light, and θ\theta is the scattering angle. The quantity hmec\frac{h}{m_e c} is known as the Compton wavelength of the electron; it is equal to $2.43\cdot {10}^{-12}$ m. The wavelength shift $\lambda ‘-\lambda$ is at least zero (for $\theta =0$ °) and at most twice the Compton wavelength of the electron (for $\theta =180$ °). (The derivation of Compton’s formula is a bit lengthy and will not be covered here.)

A Photon Colliding with a Target at Rest: A photon of wavelength $\lambda$ comes in from the left, collides with a target at rest, and a new photon of wavelength $\lambda ‘\left[/latex\right]emergesatanangle\left[latex\right]\theta$ .

Because the mass-energy and momentum of a system must both be conserved, it is not generally possible for the electron simply to move in the direction of the incident photon. The interaction between electrons and high energy photons (comparable to the rest energy of the electron, 511 keV) results in the electron being given part of the energy (making it recoil), and a photon containing the remaining energy being emitted in a different direction from the original, so that the overall momentum of the system is conserved. If the scattered photon still has enough energy left, the Compton scattering process may be repeated. In this scenario, the electron is treated as free or loosely bound. Photons with an energy of this order of magnitude are in the x-ray range of the electromagnetic radiation spectrum. Therefore, you can say that Compton effects (with electrons) occur with x-ray photons.
If the photon is of lower energy, but still has sufficient energy (in general a few eV to a few keV, corresponding to visible light through soft X-rays), it can eject an electron from its host atom entirely (a process known as the photoelectric effect), instead of undergoing Compton scattering. Higher energy photons (1.022 MeV and above, in the gamma ray range) may be able to bombard the nucleus and cause an electron and a positron to be formed, a process called pair production.

X-Ray Spectra: Origins, Diffraction by Crystals, and Importance

X-ray shows its wave nature when radiated upon atomic/molecular structures and can be used to study them.

Learning Objectives

Describe interactions between X-rays and atoms

Key Takeaways

Key Points

• X rays are relatively high- frequency EM radiation. They are produced by transitions between inner-shell electron levels, which produce x rays characteristic of the atomic element, or by accelerating electrons.
• x-ray diffraction is a technique that provides the detailed information about crystallographic structure of natural and manufactured materials.
• Current research in material science and physics involves complex materials whose lattice arrangements are crucial to obtaining a superconducting material, which can be studied using x-ray crystallography.

Key Terms

• double-helix structure: The structure formed by double-stranded molecules of nucleic acids such as DNA and RNA.
• crystallography: The experimental science of determining the arrangement of atoms in solids.
• diffraction: The bending of a wave around the edges of an opening or an obstacle.

In a previous Atom on X-rays, we have seen that there are two processes by which x-rays are produced in the anode of an x-ray tube. In one process, the deceleration of electrons produces x-rays, and these x-rays are called Bremsstrahlung, or braking radiation. The second process is atomic in nature and produces characteristic x-rays, so called because they are characteristic of the anode material. The x-ray spectrum in is typical of what is produced by an x-ray tube, showing a broad curve of Bremsstrahlung radiation with characteristic x-ray peaks on it.

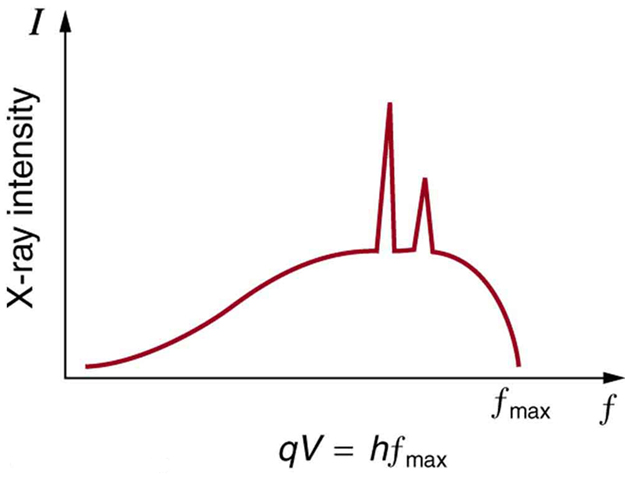
X-Ray Spectrum: X-ray spectrum obtained when energetic electrons strike a material, such as in the anode of a CRT. The smooth part of the spectrum is bremsstrahlung radiation, while the peaks are characteristic of the anode material. A different anode material would have characteristic x-ray peaks at different frequencies.

Since x-ray photons are very energetic, they have relatively short wavelengths. For example, the 54.4-keV Kα x-ray, for example, has a wavelength $\lambda =\frac{\text{hc}}{\text{E}}=0.0228$ nm. Thus, typical x-ray photons act like rays when they encounter macroscopic objects, like teeth, and produce sharp shadows. However, since atoms and atomic structures have a typical size on the order of 0.1 nm, x-ray shows its wave nature with them. The process is called x-ray diffraction because it involves the diffraction and interference of x-rays to produce patterns that can be analyzed for information about the structures that scattered the x-rays.
Shown below, Bragg’s Law gives the angles for coherent and incoherent scattering of light from a crystal lattice, which happens during x-ray diffraction. When x-ray are incident on an atom, they make the electronic cloud move as an electromagnetic wave. The movement of these charges re-radiate waves with the same frequency. This is called Rayleigh Scattering, which you should remember from a previous atom. A similar thing happens when neutron waves from the nuclei scatter from interaction with an unpaired electron. These re-emitted wave fields interfere with each other either constructively or destructively, and produce a diffraction pattern that is captured by a sensor or film. This is called the Braggs diffraction, and is the basis for x-ray diffraction.

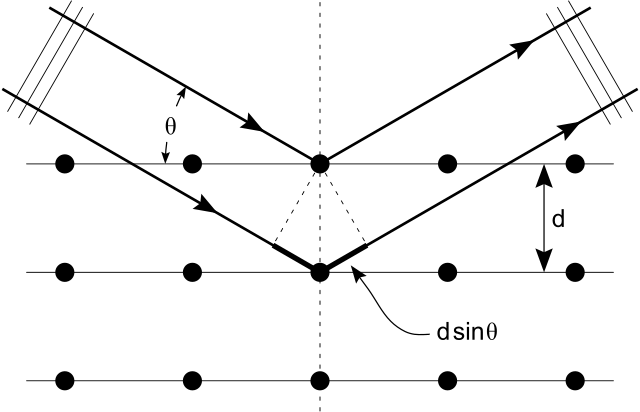
X-Ray Diffraction: Bragg’s Law of diffraction: illustration of how x-rays interact with crystal lattice.

Perhaps the most famous example of x-ray diffraction is the discovery of the double-helix structure of DNA in 1953. Using x-ray diffraction data, researchers were able to discern the structure of DNA shows a diffraction pattern produced by the scattering of x-rays from a crystal of protein. This process is known as x-ray crystallography because of the information it can yield about crystal structure. Not only do x-rays confirm the size and shape of atoms, they also give information on the atomic arrangements in materials. For example, current research in high-temperature superconductors involves complex materials whose lattice arrangements are crucial to obtaining a superconducting material. These can be studied using x-ray crystallography.

X-Ray Diffraction: X-ray diffraction from the crystal of a protein, hen egg lysozyme, produced this interference pattern. Analysis of the pattern yields information about the structure of the protein.

The Compton Effect

The Compton Effect is the phenomenon of the decrease in energy of photon when scattered by a free charged particle.

Learning Objectives

Explain why Compton scattering is an inelastic scattering.

Key Takeaways

Key Points

• Compton scattering is an example of inelastic scattering because the wavelength of the scattered light is different from the incident radiation.
• Like the photoelectric effects, the Compton effect is important because it demonstrates that light cannot be explained purely as a wave phenomenon. Light must behave as if it consists of particles to explain the Compton scattering.
• Compton’s experiment convinced physicists that light can behave as a stream of particle-like objects (quanta) whose energy is proportional to the frequency.

Key Terms

• Doppler shift: is the change in frequency of a wave for an observer moving relative to its source.
• Thomson scattering: an elastic scattering of electromagnetic radiation by a free charged particle, as described by classical electromagnetism. It is just the low-energy limit of Compton scattering
• inelastic scattering: a fundamental scattering process in which the kinetic energy of an incident particle is not conserved

Compton scattering is an inelastic scattering of a photon by a free charged particle (usually an electron). It results in a decrease in energy (increase in wavelength) of the photon (which may be an X-ray or gamma ray photon), called the Compton Effect. Part of the energy of the photon is transferred to the scattering electron. Inverse Compton scattering also exists, and happens when a charged particle transfers part of its energy to a photon.

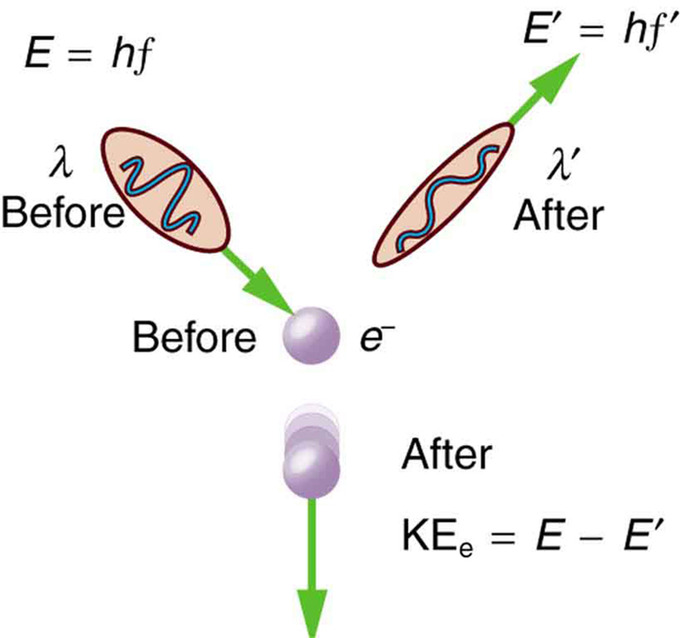
Scattering in the Compton Effect: The Compton Effect is the name given to the scattering of a photon by an electron. Energy and momentum are conserved, resulting in a reduction of both for the scattered photon. Studying this effect, Compton verified that photons have momentum.

Compton scattering is an example of inelastic scattering because the wavelength of the scattered light is different from the incident radiation. Still, the origin of the effect can be considered as an elastic collision between a photon and an electron. The amount of change in the wavelength is called the Compton shift. Although nuclear Compton scattering exists, Compton scattering usually refers to the interaction involving only the electrons of an atom.
The Compton effect is important because it demonstrates that light cannot be explained purely as a wave phenomenon. Thomson scattering, the classical theory of an electromagnetic wave scattered by charged particles, cannot explain low intensity shifts in wavelength: classically, light of sufficient intensity for the electric field to accelerate a charged particle to a relativistic speed will cause radiation-pressure recoil and an associated Doppler shift of the scattered light. However, the effect will become arbitrarily small at sufficiently low light intensities regardless of wavelength. Light must behave as if it consists of particles to explain the low-intensity Compton scattering. Compton’s experiment convinced physicists that light can behave as a stream of particle-like objects (quanta) whose energy is proportional to the frequency.

 

 

Atomic Physics and Quantum Mechanics

Wave Nature of Matter Causes Quantization

The wave nature of matter is responsible for the quantization of energy levels in bound systems.

Learning Objectives

Explain relationship between the wave nature of matter and the quantization of energy levels in bound systems

Key Takeaways

Key Points

• Strings in musical instruments (guitar, for example) can only produce a very specific set of pitches because only waves of a certain wavelength can “fit” on the string of a given length with fixed ends.
• Similarly, once an electron is bound by a Coulomb potential of a nucleus, it no longer can have any arbitrary wavelength because the wave should satisfy a certain boundary condition.
• Bohr’s quantization assumption can be derived from the condition for constructive intereference of an electron matter wave in a circular orbit.

Key Terms

• quantization: The process of explaining a classical understanding of physical phenomena in terms of a newer understanding known as quantum mechanics.
• angular momentum: A vector quantity describing an object in circular motion; its magnitude is equal to the momentum of the particle, and the direction is perpendicular to the plane of its circular motion.
• matter wave: A concept reflects the wave-particle duality of matter. The theory was proposed by Louis de Broglie.

To consider why wave nature of matter in bound systems leads to quantization, let’s consider an example in classical mechanics. We will look at a basic string “instrument” (a string pulled tight and fixed at both ends). If a string was free and not attached to anything, we know that it could oscillate at any driven frequency. However, the string in this example (with fixed ends and specific length) can only produce a very specific set of pitches because only waves of a certain wavelength can “fit” on the string of a given length with fixed ends. Once the string becomes a “bound system” with specific boundary restrictions, it allows waves with only a discrete set of frequencies.
This is the exact mechanism that causes quantization in atoms. The wave nature of matter is responsible for the quantization of energy levels in bound systems. Just like a free string, the matter wave of a free electron can have any wavelength, determined by its momentum. However, once an electron is “bound” by a Coulomb potential of a nucleus, it can no longer have an arbitrary wavelength as the wave needs to satisfy a certain boundary condition. Only those states where matter interferes constructively (leading to standing waves) exist, or are “allowed” (see illustration in.

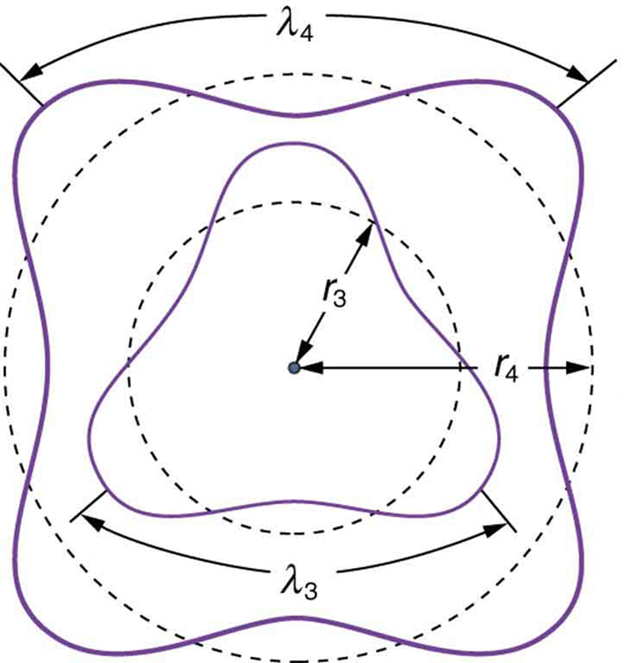
Fig 2: The third and fourth allowed circular orbits have three and four wavelengths, respectively, in their circumferences.

Assuming that an integral multiple of the electron’s wavelength equals the circumference of the orbit, we have:
[latex]\text{n}\lambda_\text{n} = 2\pi \text{r}_\text{n} (\text{n} = 1,2,3,…)[/latex]
Substituting $\lambda =\frac{\text{h}}{{\text{m}}_{\text{e}}\text{v}}$ , this becomes:
$\frac{\text{nh}}{{\text{m}}_{\text{ev}}}=2\pi {\text{r}}_{\text{n}}$
The angular momentum is $\text{L}={\text{m}}_{\text{e}}\text{v}\text{r}$ , therefore we obtain the quantization of angular momentum:
[latex]\displaystyle \text{L} = \text{m}_\text{e} \text{v} \text{r}_\text{n} = \text{n} \frac{\text{h}}{2\pi} (\text{n} = 1,2,3,…)[/latex]
As previously discussed, Bohr was forced to hypothesize this as the rule for allowed orbits. We now realize this as a condition for constructive interference of an electron in a (bound) circular orbit.

Photon Interactions and Pair Production

Pair production refers to the creation of an elementary particle and its antiparticle, usually when a photon interacts with a nucleus.

Learning Objectives

Describe process of pair production as the result of photon interaction with nucleus

Key Takeaways

Key Points

• The probability of pair production in photon -matter interactions increases with increasing photon energy, and also increases with atomic number of the nucleus approximately as $\text{Z}$ .
• Energy and momentum should be conserved through the pair production process. Some other conserved quantum numbers such as angular momentum, electric charge, etc., must sum to zero as well.
• Nucleus is needed in the pair production of electron and positron to satisfy the energy and momentum conservation laws.

Key Terms

• gamma ray: A very high frequency (and therefore very high energy) electromagnetic radiation emitted as a consequence of radioactivity.
• positron: The antimatter equivalent of an electron, having the same mass but a positive charge.

Below is an illustration of pair production, which refers to the creation of an elementary particle and its antiparticle, usually when a photon interacts with a nucleus. For example, an electron and its antiparticle, the positron, may be created. This is allowed, provided there is enough energy available to create the pair (i.e., the total rest mass energy of the two particles) and that the situation allows both energy and momentum to be conserved. Some other conserved quantum numbers such as angular momentum, electric charge, etc., must sum to zero as well. The probability of pair production in photon-matter interactions increases with increasing photon energy, and also increases with atomic number ($\text{Z}$ ) of the nucleus approximately as ${\text{Z}}^2$ .

Pair Production: Feynman diagram for pair production. A photon decays into an electron-positron pair.

$\gamma +\gamma \to {\text{e}}^{-}+{\text{e}}^{+}$

In nuclear physics, this reaction occurs when a high-energy photon ( gamma rays ) interacts with a nucleus. The energy of this photon can be converted into mass through Einstein’s equation $\text{E}={\text{mc}}^2$ where $\text{E}$ is energy, $\text{m}$ is mass and $\text{c}$ is the speed of light. The photon must have enough energy to create the mass of an electron plus a positron. The mass of an electron is $9.11\cdot {10}^{-31}$ kg (equivalent to 0.511 MeV in energy), the same as a positron.
Without a nucleus to absorb momentum, a photon decaying into electron-positron pair (or other pairs for that matter) can never conserve energy and momentum simultaneously. The nucleus in the process carries away (or provides) access momentum.
The reverse process is also possible. The electron and positron can annihilate and produce two 0.511 MeV gamma photons. If all three gamma rays, the original with its energy reduced by 1.022 MeV and the two annihilation gamma rays, are detected simultaneously, then a full energy peak is observed.
These interactions were first observed in Patrick Blackett’s counter-controlled cloud chamber, leading him to receive the 1948 Nobel Prize in Physics.

 

 

Electron Microscopes

An electron microscope is a microscope that uses an electron beam to create an image of the target.

Learning Objectives

Explain why electron microscopes provide higher resolution than optical microscopes

Key Takeaways

Key Points

• Electron microscopes are very useful as they are able to magnify objects to a much higher resolution than optical ones.
• Higher resolution can be achieved with electron microscopes because the de Broglie wavelengths for electrons are so much smaller than that of visible light.
• In electron microscopes, electromagnets can be used as magnetic lenses to manipulate electron beams.

Key Terms

• CCD: A charge-coupled device (CCD) is a device for the movement of electrical charge, usually from within the device to an area where the charge can be manipulated, for example conversion into a digital value. The CCD is a major technology required for digital imaging.
• de Broglie wavelength: The wavelength of a matter wave is inversely proportional to the momentum of a particle and is called a de Broglie wavelength.

We have seen that under certain circumstances particles behave like waves. This idea is used in the electron microscope which is a type that uses electrons to create an image of the target. It has much higher magnification or resolving power than a normal light microscope. It can achieve better than 50 pm resolution and magnifications of up to about 10,000,000 times, whereas ordinary, nonconfocal light microscopes are limited by diffraction to about 200 nm resolution and useful magnifications below 2000 times.

Electron Microscope Image: An image of an ant in a scanning electron microscope.

Let’s first review how a regular optical microscope works. A beam of light is shone through a thin target and the image is then magnified and focused using objective and ocular lenses. The amount of light which passes through the target depends on its densities, since the less dense regions allow more light to pass through than the denser regions. This means that the beam of light which is partially transmitted through the target carries information about the inner structure of the target.

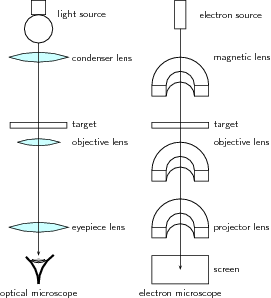
Optical and Electron Microscopes: Diagram of the basic components of an optical microscope and an electron microscope.

The original form of electron microscopy, transmission electron microscopy, works in a similar manner using electrons. In the electron microscope, electrons which are emitted by a cathode are formed into a beam using magnetic lenses (usually electromagnets). This electron beam is then passed through a very thin target. Again, the regions in the target with higher densities stop the electrons more easily. So, the number of electrons which pass through the different regions of the target depends on their densities. This means that the partially transmitted beam of electrons carries information about the densities of the inner structure of the target.

The spatial variation in this information (the “image”) is then magnified by a series of magnetic lenses and it is recorded by hitting a fluorescent screen, photographic plate, or light-sensitive sensor such as a CCD (charge-coupled device) camera. The image detected by the CCD may be displayed in real time on a monitor or computer.

Electron microscopes are very useful as they are able to magnify objects to a much higher resolution. This is because their de Broglie wavelengths are so much smaller than that of visible light. You hopefully remember that light is diffracted by objects which are separated by a distance of about the same size as the wavelength of the light. This diffraction then prevents you from being able to focus the transmitted light into an image.

Therefore, the sizes at which diffraction occurs for a beam of electrons is much smaller than those for visible light. This is why you can magnify targets to a much higher order of magnification using electrons rather than visible light.

Lasers

A laser consists of a gain medium, a mechanism to supply energy to it, and something to provide optical feedback.

Learning Objectives

Describe basic parts of laser

Key Takeaways

Key Points

• The gain medium is where the optical amplification process occurs. Gas and semiconductors are commonly used gain media.
• The most common type of laser uses feedback from an optical cavity–a pair of highly reflective mirrors on either end of the gain medium. A single photon can bounce back and forth between the mirrors many times, passing through the gain medium and being amplified each time.
• Lasers are ubiquitous, finding utility in thousands of highly varied applications in every section of modern society.

Key Terms

• stimulated emission: The process by which an atomic electron (or an excited molecular state) interacting with an electromagnetic wave of a certain frequency may drop to a lower energy level, transferring its energy to that field.

When lasers were invented in 1960, they were called “a solution looking for a problem. ” Nowadays, lasers are ubiquitous, finding utility in thousands of highly varied applications in every section of modern society, including consumer electronics, information technology, science, medicine, industry, law enforcement, entertainment, and the military.
Having examined stimulated emission and optical amplification process in the “Lasers, Applications of Quantum Mechanics” section, this atom looks at how lasers are built.
A laser consists of a gain medium, a mechanism to supply energy to it, and something to provide optical feedback (usually an optical cavity). When a gain medium is placed in an optical cavity, a laser can then produce a coherent beam of photons.
The gain medium is where the optical amplification process occurs. It is excited by an external source of energy into an excited state (called “population inversion”), ready to be fired when a photon with the right frequency enters the medium. In most lasers, this medium consists of a population of atoms which have been excited by an outside light source or an electrical field which supplies energy for atoms to absorb in order to be transformed into excited states. There are many types of lasers depending on the gain media and mode of operation. Gas and semiconductors are commonly used gain media.

Wavelengths of Commercially Available Lasers: Laser types with distinct laser lines are shown above the wavelength bar, while below are shown lasers that can emit in a wavelength range. The height of the lines and bars gives an indication of the maximal power/pulse energy commercially available, while the color codifies the type of laser material.

The most common type of laser uses feedback from an optical cavity–a pair of highly reflective mirrors on either end of the gain medium. A single photon can bounce back and forth between the mirrors many times, passing through the gain medium and being amplified each time. Typically one of the two mirrors, the output coupler, is partially transparent. Some of the light escapes through this mirror, producing a laser beam that is visible to the naked eye.

 

Multielectron Atoms

Multielectron Atoms

Atoms with more than one electron are referred to as multielectron atoms.

Learning Objectives

Describe atomic structure and shielding in multielectron atoms

Key Takeaways

Key Points

• Hydrogen is the only atom in the periodic table that has one electron in the orbitals under ground state.
• In multielectron atoms, the net force on electrons in the outer shells is reduced due to shielding.
• The effective nuclear charge on each electron can be approximated as: ${\text{Z}}_{\text{eff}}=\text{Z}-\sigma$ , where $\text{Z}$ is the number of protons in the nucleus and $\sigma$ is the average number of electrons between the nucleus and the electron in question.

Key Terms

• hydrogen-like: having a single electron
• electron shell: The collective states of all electrons in an atom having the same principal quantum number (visualized as an orbit in which the electrons move).
• valence shell: the outermost shell of electrons in an atom; these electrons take part in bonding with other atoms

Multielectron Atoms

Atoms with more than one electron, such as Helium (He) and Nitrogen (N), are referred to as multielectron atoms. Hydrogen is the only atom in the periodic table that has one electron in the orbitals under ground state.
In hydrogen-like atoms (those with only one electron), the net force on the electron is just as large as the electric attraction from the nucleus. However, when more electrons are involved, each electron (in the $\text{n}$ -shell) feels not only the electromagnetic attraction from the positive nucleus, but also repulsion forces from other electrons in shells from ‘1’ to ‘[latex]\text{n}[/latex]‘. This causes the net force on electrons in the outer electron shells to be significantly smaller in magnitude. Therefore, these electrons are not as strongly bonded to the nucleus as electrons closer to the nucleus. This phenomenon is often referred to as the Orbital Penetration Effect. The shielding theory also explains why valence shell electrons are more easily removed from the atom.

Electron Shielding Effect: A multielectron atom with inner electrons shielding outside electrons from the positively charged nucleus

The size of the shielding effect is difficult to calculate precisely due to effects from quantum mechanics. As an approximation, the effective nuclear charge on each electron can be estimated by: Zeff=Z−σZ_\text{eff} = Z – \sigma, where $\text{Z}$ is the number of protons in the nucleus and σ\sigma is the average number of electrons between the nucleus and the electron in question. σ\sigma can be found by using quantum chemistry and the Schrodinger equation or by using Slater’s empirical formula.
For example, consider a sodium cation, a fluorine anion, and a neutral neon atom. Each has 10 electrons, and the number of nonvalence electrons is two (10 total electrons minus eight valence electrons), but the effective nuclear charge varies because each has a different number of protons:
${\text{Z}}_{\text{eff}}{\text{F}}^{-}=9-2=7+$
${\text{Z}}_{\text{eff}}\text{Ne}=10-2=8+$
${\text{Z}}_{\text{eff}}{\text{Na}}^{+}=11-2=9+$
As a consequence, the sodium cation has the largest effective nuclear charge and, therefore, the smallest atomic radius.

The Periodic Table

A periodic table is the arrangement of chemical elements according to their electron configurations and recurring chemical properties.

Learning Objectives

Explain how elements are arranged in the Periodic Table.

Key Takeaways

Key Points

• A periodic table provides a useful framework for analyzing the chemical behavior of elements.
• A periodic table includes only chemical elements with each chemical element assigned a unique atomic number representing the number of protons in its nucleus.
• Dmitri Mendeleev is credited with the publication of the first widely recognized periodic table in 1869.

Key Terms

• periodic table: A tabular chart of the chemical elements according to their atomic numbers so that elements with similar properties are in the same column.
• element: Any one of the simplest chemical substances that cannot be decomposed in a chemical reaction or by any chemical means and made up of atoms all having the same number of protons.
• atomic number: The number, equal to the number of protons in an atom that determines its chemical properties. Symbol: $\text{Z}$

A periodic table is a tabular display of the chemical elements, organized on the basis of their atomic numbers, electron configurations, and recurring chemical properties. Elements are presented according to their atomic numbers (number of protons) in increasing order. The standard form of the table comprises an eighteen by seven grid or main body of elements, positioned above a smaller double row of elements. The table can also be deconstructed into four rectangular blocks: the s-block to the left, the p-block to the right, the d-block in the middle, and the f-block below that. The rows of the table are called periods. The columns of the s-, d-, and p-blocks are called groups, some of which have names such as the halogens or the noble gases.
Since, by definition, a periodic table incorporates recurring trends, any such table can be used to derive relationships between the properties of the elements and predict the properties of new elements that are yet to be discovered or synthesized. As a result, a periodic table, in the standard form or some other variant, provides a useful framework for analyzing chemical behavior. Such tables are widely used in chemistry and other sciences.

Periodic Table of Elements: The standard form of the periodic table, where the colors represent different categories of elements

The Specifics of the Periodic Table

All versions of the periodic table include only chemical elements, rather than mixtures, compounds, or subatomic particles. Each chemical element has a unique atomic number representing the number of protons in its nucleus. Most elements have differing numbers of neutrons among different atoms: these variants are referred to as isotopes. For example, carbon has three naturally occurring isotopes. All of its atoms have six protons and most have six neutrons as well, but about one percent have seven neutrons, and a very small fraction have eight neutrons. Isotopes are never separated in the periodic table. They are always grouped together under a single element. Elements with no stable isotopes have the atomic masses of their most stable isotopes listed in parentheses.
All elements from atomic numbers ‘1’ (hydrogen) to ‘118’ (ununoctium) have been discovered or synthesized. Of these, elements up through californium exist naturally; the rest have only been synthesized in laboratories. The production of elements beyond ununoctium is being pursued. The question of how the periodic table may need to be modified to accommodate any such additions is a matter of ongoing debate. Numerous synthetic radionuclides of naturally occurring elements have also been produced in laboratories.
Although precursors exist, Dmitri Mendeleev is generally credited with the publication of the first widely recognized periodic table in 1869. He developed his table to illustrate periodic trends in the properties of the elements known at the time. Mendeleev also predicted some properties of then-unknown elements that were expected to fill gaps in the table. Most of his predictions were proved correct when the elements in question were subsequently discovered. Mendeleev’s periodic table has since been expanded and refined with the discovery or synthesis of more new elements and the development of new theoretical models to explain chemical behavior.

Mendeleev’s 1869 Periodic Table: Mendeleev’s 1869 periodic table presents the periods vertically and the groups horizontally.

Dmitri Mendeleev: Dmitri Mendeleev is known for publishing a widely recognized periodic table.

Electron Configurations

The electron configuration is the distribution of electrons of an atom or molecule in atomic or molecular orbitals.

Learning Objectives

Explain the meaning of electron configurations

Key Takeaways

Key Points

• Electrons fill atomic orbitals according to the Aufbau principle in atoms.
• For systems with only one electron, an energy is associated with each electron configuration and electrons are able to move from one configuration to another by emission or absorption of a quantum of energy, in the form of a photon.
• For atoms or molecules with more than one electron, an infinite number of electronic configurations are needed to exactly describe any multi-electron system, and no energy can be associated with one single configuration.

Key Terms

• electron shell: The collective states of all electrons in an atom having the same principal quantum number (visualized as an orbit in which the electrons move).
• atomic orbital: The quantum mechanical behavior of an electron in an atom describing the probability of the electron’s particular position and energy.

The electron configuration is the distribution of electrons of an atom or molecule in atomic or molecular orbitals. Electron configurations describe electrons as each moving independently in an orbital, in an average field created by all other orbitals.
In atoms, electrons fill atomic orbitals according to the Aufbau principle (shown in ), stated as: a maximum of two electrons are put into orbitals in the order of increasing orbital energy—the lowest-energy orbitals are filled before electrons are placed in higher-energy orbitals. As an example, the electron configuration of the neon atom is 1s² 2s² 2p⁶ or [He]2s² 2p⁶, as diagramed in. In molecules, the situation becomes more complex, as each molecule has a different orbital structure. The molecular orbitals are labelled according to their symmetry, rather than the atomic orbital labels used for atoms and monoatomic ions: hence, the electron configuration of the diatomic oxygen molecule, O₂, is 1σ_g² 1σ_u² 2σ_g² 2σ_u² 1π_u⁴ 3σ_g² 1π_g2.

Electron Configuration of Neon Atom: Electron configuration of neon atom showing only outer electron shell.

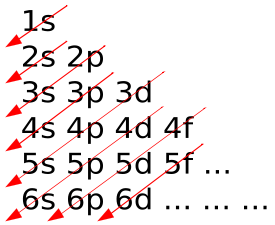
Aufbau Principle: In the Aufbau Principle, as electrons are added to atoms, they are added to the lowest orbitals first.

According to the laws of quantum mechanics, for systems with only one electron, an energy is associated with each electron configuration and, upon certain conditions, electrons are able to move from one configuration to another by emission or absorption of a quantum of energy, in the form of a photon.
For atoms or molecules with more than one electron, the motion of electrons are correlated and such picture is no longer exact. An infinite number of electronic configurations are needed to exactly describe any multi-electron system, and no energy can be associated with one single configuration. However, the electronic wave function is usually dominated by a very small number of configurations and therefore the notion of electronic configuration remains essential for multi-electron systems.
Electronic configuration of polyatomic molecules can change without absorption or emission of photon through vibronic couplings.
Knowledge of the electron configuration of different atoms is useful in understanding the structure of the periodic table of elements. The outermost electron shell is often referred to as the valence shell and (to a first approximation) determines the chemical properties. It should be remembered that the similarities in the chemical properties were remarked more than a century before the idea of electron configuration. The concept of electron configuration is also useful for describing the chemical bonds that hold atoms together. In bulk materials this same idea helps explain the peculiar properties of lasers and semiconductors.  

 

The Nucleus

Nuclear Size and Density

Nuclear size is defined by nuclear radius; nuclear density can be calculated from nuclear size.

Learning Objectives

Explain relationship between nuclear radius, nuclear density, and nuclear size.

Key Takeaways

Key Points

• The first estimate of a nuclear charge radius was made by Hans Geiger and Ernest Marsden in 1909, under the direction of Ernest Rutherford, in the gold foil experiment that involved the scattering of α-particles by gold foil, as shown in Figure 1.
• An empirical relation exists between the charge radius and the mass number, $\text{A}$ , for heavier nuclei ($\text{A}>20$ ): where $\text{r}$ is an empirical constant of 1.2–1.5 fm.
• The nuclear density for a typical nucleus can be approximately calculated from the size of the nucleus: $\text{n}=\frac{\text{A}}{\frac{4}{3}\pi {\text{R}}^3}$

Key Terms

• α-particle: two protons and two neutrons bound together into a particle identical to a helium nucleus
• atomic spectra: emission or absorption lines formed when an electron makes a transition from one energy level of an atom to another
• nucleus: the massive, positively charged central part of an atom, made up of protons and neutrons

Nuclear size is defined by nuclear radius, also called rms charge radius. It can be measured by the scattering of electrons by the nucleus and also inferred from the effects of finite nuclear size on electron energy levels as measured in atomic spectra.
The problem of defining a radius for the atomic nucleus is similar to the problem of atomic radius, in that neither atoms nor their nuclei have definite boundaries. However, the nucleus can be modelled as a sphere of positive charge for the interpretation of electron scattering experiments: because there is no definite boundary to the nucleus, the electrons “see” a range of cross-sections, for which a mean can be taken. The qualification of “rms” (for “root mean square”) arises because it is the nuclear cross-section, proportional to the square of the radius, which is determining for electron scattering.
The first estimate of a nuclear charge radius was made by Hans Geiger and Ernest Marsden in 1909, under the direction of Ernest Rutherford at the Physical Laboratories of the University of Manchester, UK. The famous Rutherford gold foil experiment involved the scattering of α-particles by gold foil, with some of the particles being scattered through angles of more than 90°, that is coming back to the same side of the foil as the α-source, as shown in Figure 1. Rutherford was able to put an upper limit on the radius of the gold nucleus of 34 femtometers (fm).
Later studies found an empirical relation between the charge radius and the mass number, $\text{A}$ , for heavier nuclei ($\text{A}>20$ ): $\text{R}\approx \text{r}\cdot {\text{A}}^{1/3}$ where $\text{r}$ is an empirical constant of 1.2–1.5 fm. This gives a charge radius for the gold nucleus ($\text{A}=197$ ) of about 7.5 fm.
Nuclear density is the density of the nucleus of an atom, averaging about $4\cdot {10}^{17}\text{kg/}{\text{m}}^3$ . The nuclear density for a typical nucleus can be approximately calculated from the size of the nucleus:
$\text{n}=\frac{\text{A}}{\frac{4}{3}\pi {\text{R}}^3}$

Nuclear Stability

The stability of an atom depends on the ratio and number of protons and neutrons, which may represent closed and filled quantum shells.

Learning Objectives

Explain the relationship between the stability of an atom and its atomic structure.

Key Takeaways

Key Points

• Most odd-odd nuclei are highly unstable with respect to beta decay because the decay products are even-even and therefore more strongly bound, due to nuclear pairing effects.
• An atom with an unstable nucleus is characterized by excess energy available either for a newly created radiation particle within the nucleus or via internal conversion.
• All elements form a number of radionuclides, although the half-lives of many are so short that they are not observed in nature.

Key Terms

• nuclide: A nuclide (from “nucleus”) is an atomic species characterized by the specific constitution of its nucleus — i.e., by its number of protons ($\text{Z}$ ), its number of neutrons ($\text{N}$ ), and its nuclear energy state.
• radionuclide: A radionuclide is an atom with an unstable nucleus, characterized by excess energy available to be imparted either to a newly created radiation particle within the nucleus or via internal conversion.
• radioactive decay: any of several processes by which unstable nuclei emit subatomic particles and/or ionizing radiation and disintegrate into one or more smaller nuclei

The stability of an atom depends on the ratio of its protons to its neutrons, as well as on whether it contains a “magic number” of neutrons or protons that would represent closed and filled quantum shells. These quantum shells correspond to energy levels within the shell model of the nucleus. Filled shells, such as the filled shell of 50 protons in the element tin, confers unusual stability on the nuclide. Of the 254 known stable nuclides, only four have both an odd number of protons and an odd number of neutrons:

• hydrogen-2 (deuterium)
• lithium-6
• boron-10
• nitrogen-14

Also, only four naturally occurring, radioactive odd-odd nuclides have a half-life greater than a billion years:

• potassium-40
• vanadium-50
• lanthanum-138
• tantalum-180m

Alpha Decay: Alpha decay is one type of radioactive decay. An atomic nucleus emits an alpha particle and thereby transforms (“decays”) into an atom with a mass number smaller by four and an atomic number smaller by two. Many other types of decay are possible.

Most odd-odd nuclei are highly unstable with respect to beta decay because the decay products are even-even and therefore more strongly bound, due to nuclear pairing effects.
An atom with an unstable nucleus, called a radionuclide, is characterized by excess energy available either for a newly created radiation particle within the nucleus or via internal conversion. During this process, the radionuclide is said to undergo radioactive decay. Radioactive decay results in the emission of gamma rays and/or subatomic particles such as alpha or beta particles, as shown in. These emissions constitute ionizing radiation. Radionuclides occur naturally but can also be produced artificially.
All elements form a number of radionuclides, although the half-lives of many are so short that they are not observed in nature. Even the lightest element, hydrogen, has a well-known radioisotope: tritium. The heaviest elements (heavier than bismuth) exist only as radionuclides. For every chemical element, many radioisotopes that do not occur in nature (due to short half-lives or the lack of a natural production source) have been produced artificially.

Binding Energy and Nuclear Forces

Nuclear force is the force that is responsible for binding of protons and neutrons into atomic nuclei.

Learning Objectives

Explain how nuclear force varies with distance.

Key Takeaways

Key Points

• The nuclear force is powerfully attractive at distances of about 1 femtometer (fm), rapidly decreases to insignificance at distances beyond about 2.5 fm, and becomes repulsive at very short distances less than 0.7 fm.
• The nuclear force is a residual effect of the a strong interaction that binds together particles called quarks into nucleons.
• The binding energy of nuclei is always a positive number while the mass of an atom ‘s nucleus is always less than the sum of the individual masses of the constituent protons and neutrons when separated.

Key Terms

• nucleus: the massive, positively charged central part of an atom, made up of protons and neutrons
• quark: In the Standard Model, an elementary subatomic particle that forms matter. Quarks are never found alone in nature, but combine to form hadrons, such as protons and neutrons.
• gluon: A massless gauge boson that binds quarks together to form baryons, mesons and other hadrons; it is associated with the strong nuclear force.

The nuclear force is the force between two or more component parts of an atomic nuclei. The component parts are neutrons and protons, which collectively are called nucleons. Nuclear force is responsible for the binding of protons and neutrons into atomic nuclei.

Drawing of Atomic Nucleus: A model of the atomic nucleus showing it as a compact bundle of the two types of nucleons: protons (red) and neutrons (blue).

To disassemble a nucleus into unbound protons and neutrons would require working against the nuclear force. Conversely, energy is released when a nucleus is created from free nucleons or other nuclei—known as the nuclear binding energy. The binding energy of nuclei is always a positive number, since all nuclei require net energy to separate into individual protons and neutrons. Because of mass-energy equivalence (i.e., Einstein’s famous formula $\text{E}={\text{mc}}^2$ ), releasing this energy causes the mass of the nucleus to be lower than the total mass of the individual nucleons (leading to “mass deficit”). Binding energy is the energy used in nuclear power plants and nuclear weapons.
The nuclear force is powerfully attractive between nucleons at distances of about 1 femtometer (fm) between their centers, but rapidly decreases to relative insignificance at distances beyond about 2.5 fm. At very short distances (less than 0.7 fm) it becomes repulsive; it is responsible for the physical size of nuclei since the nucleons can come no closer than the force allows.
The nuclear force is now understood as a residual effect of an even more powerful “strong force” or strong interaction. It is the attractive force that binds together particles known as quarks (to form the nucleons themselves). This more powerful force is mediated by particles called gluons. Gluons hold quarks together with a force like that of an electric charge (but of far greater power).
The nuclear forces arising between nucleons are now seen as analogous to the forces in chemistry between neutral atoms or molecules (called London forces). Such forces between atoms are much weaker than the attractive electrical forces that hold together the atoms themselves (i.e., that bind electrons to the nucleus), and their range between atoms is shorter because they arise from a small separation of charges inside the neutral atom.
Similarly, even though nucleons are made of quarks in combinations which cancel most gluon forces (they are “color neutral”), some combinations of quarks and gluons leak away from nucleons in the form of short-range nuclear force fields that extend from one nucleon to another nucleon in close proximity. These nuclear forces are very weak compared to direct gluon forces (“color forces” or “strong forces”) inside nucleons, and the nuclear forces extend over only a few nuclear diameters, falling exponentially with distance. Nevertheless, they are strong enough to bind neutrons and protons over short distances, as well as overcome the electrical repulsion between protons in the nucleus. Like London forces, nuclear forces also stop being attractive, and become repulsive when nucleons are brought too close together.

 

 

Radioactivity

Natural Radioactivity

Detectable amounts of radioactive material occurs naturally in soil, rocks, water, air, and vegetation.

Learning Objectives

Name major sources of terrestrial radiation.

Key Takeaways

Key Points

• The biggest source of natural background radiation is airborne radon, a radioactive gas that emanates from the ground.
• The earth is constantly bombarded by radiation from outer space that consists of positively charged ions ranging from protons to iron and larger nuclei from sources outside of our solar system.
• Terrestrial radiation includes sources that remain external to the body. The major radionuclides of concern are potassium, uranium, and thorium and their decay products.

Key Terms

• radionuclide: A radionuclide is an atom with an unstable nucleus, characterized by excess energy available to be imparted either to a newly created radiation particle within the nucleus or via internal conversion.
• radon: a radioactive chemical element (symbol Rn, formerly Ro) with atomic number 86; one of the noble gases
• sievert: in the International System of Units, the derived unit of radiation dose; the dose received in one hour at a distance of 1 cm from a point source of 1 mg of radium in a 0.5 mm thick platinum enclosure; symbol: Sv

Radioactive material is found throughout nature. Detectable amounts occur naturally in soil, rocks, water, air, and vegetation. From these sources it can be inhaled and ingested into the body. In addition to this internal exposure, humans also receive external exposure from radioactive materials that remain outside the body and from cosmic radiation from space. The worldwide average natural dose to humans is about 2.4 millisieverts (mSv) per year. This is four times more than the worldwide average artificial radiation exposure, which in the year 2008 amounted to about 0.6 mSv per year. In some wealthier countries, such as the US and Japan, artificial exposure is, on average, greater than the natural exposure, due to greater access to medical imaging. In Europe, the average natural background exposure by country ranges from under 2 mSv annually in the United Kingdom to more than 7 mSv annually in Finland, as shown in.

Natural Radiation Atlas of Europe: Bar chart of average annual dosages from natural radiation sources for major European countries

Natural Background Radiation

The biggest source of natural background radiation is airborne radon, a radioactive gas that emanates from the ground. Radon and its isotopes, parent radionuclides, and decay products all contribute to an average inhaled dose of 1.26 mSv/a. Radon is unevenly distributed and variable with weather, such that much higher doses occur in certain areas of the world. In these areas it can represent a significant health hazard. Concentrations over 500 times higher than the world average have been found inside buildings in Scandinavia, the United States, Iran, and the Czech Republic. Radon is a decay product of uranium, which is relatively common in the Earth’s crust but more concentrated in ore-bearing rocks scattered around the world. Radon seeps out of these ores into the atmosphere or into ground water; it can also infiltrate into buildings. It can be inhaled into the lungs, along with its decay products, where it will reside for a period of time after exposure.

Radiation from Outer Space

In addition, the earth, and all living things on it, are constantly bombarded by radiation from outer space. This radiation primarily consists of positively charged ions ranging from protons to iron and larger nuclei derived from sources outside of our solar system. This radiation interacts with atoms in the atmosphere to create an air shower of secondary radiation, including x-rays, muons, protons, alpha particles, pions, electrons, and neutrons. The immediate dose from cosmic radiation is largely from muons, neutrons, and electrons, and this dose varies in different parts of the world based on the geomagnetic field and altitude. This radiation is much more intense in the upper troposphere (around 10 km in altitude) and is therefore of particular concern for airline crews and frequent passengers, who spend many hours per year in this environment. An airline crew typically gets an extra dose on the order of 2.2 mSv (220 mrem) per year.

Terrestrial Radiation

Terrestrial radiation only includes sources that remain external to the body. The major radionuclides of concern are potassium, uranium, and thorium and their decay products. Some of these decay products, like radium and radon, are intensely radioactive but occur in low concentrations. Most of these sources have been decreasing, due to radioactive decay since the formation of the earth, because there is no significant source of replacement. Because of this, the present activity on Earth from uranium-238 is only half as much as it originally was because of its 4.5-billion-year half-life. Potassium-40 (with a half-life of 1.25 billion years) is at about eight percent of its original activity. However, the effects on humans of the actual diminishment (due to decay) of these isotopes is minimal. This is because humans evolved too recently for the difference in activity over a fraction of a half-life to be significant. Put another way, human history is so short in comparison to a half-life of a billion years that the activity of these long-lived isotopes has been effectively constant throughout our time on this planet.
Many shorter-half-life and therefore more intensely radioactive isotopes have not decayed out of the terrestrial environment because they are still being produced. Examples of these are radium-226 (a decay product of uranium-238) and radon-222 (a decay product of radium-226).

Radiation Detection

A radiation detector is a device used to detect, track, or identify high-energy particles.

Learning Objectives

Explain difference between major types of radiation detectors.

Key Takeaways

Key Points

• Gaseous ionization detectors use the ionizing effect of radiation upon gas-filled sensors.
• A semiconductor detector uses a semiconductor (usually silicon or germanium) to detect traversing charged particles or the absorption of photons.
• A scintillation detector is created by coupling a scintillator to an electronic light sensor.

Key Terms

• scintillator: any substance that glows under the action of photons or other high-energy particles
• diode: an electronic device that allows current to flow in one direction only; a valve
• semiconductor: A substance with electrical properties intermediate between a good conductor and a good insulator.

A radiation detector is a device used to detect, track, or identify high- energy particles, such as those produced by nuclear decay, cosmic radiation, and reactions in a particle accelerator. Modern detectors are also used as calorimeters to measure the energy of detected radiation. They may be also used to measure other attributes, such as momentum, spin, and charge of the particles. Different types of radiation detectors exist; gaseous ionization detectors, semiconductor detectors, and scintillation detectors are the most common.

Different Types of Radiation Detectors: different types of radiation detectors (counters)

Gaseous Ionization Detectors

Gaseous ionization detectors use the ionizing effect of radiation upon gas-filled sensors. If a particle has enough energy to ionize a gas atom or molecule, the resulting electrons and ions cause a current flow, which can be measured.

Semiconductor Detectors

A semiconductor detector uses a semiconductor (usually silicon or germanium) to detect traversing charged particles or the absorption of photons. When these detectors’ sensitive structures are based on single diodes, they are called semiconductor diode detectors. When they contain many diodes with different functions, the more general term “semiconductor detector” is used. Semiconductor detectors have had various applications in recent decades, in particular in gamma and x-ray spectrometry and as particle detectors.

Scintillation Detectors

A scintillation detector is created by coupling a scintillator — a material that exhibits luminescence when excited by ionizing radiation — to an electronic light sensor, such as a photomultiplier tube (PMT) or a photodiode. PMTs absorb the light emitted by the scintillator and re-emit it in the form of electrons via the photoelectric effect. The subsequent multiplication of those electrons (sometimes called photo-electrons) results in an electrical pulse, which can then be analyzed. The pulse yields meaningful information about the particle that originally struck the scintillator.
Scintillators are used by the American government, particularly Homeland Security, as radiation detectors. Scintillators can also be used in neutron and high-energy particle physics experiments, new energy resource exploration, x-ray security, nuclear cameras, computed tomography, and gas exploration. Other applications of scintillators include CT scanners and gamma cameras in medical diagnostics, screens in computer monitors, and television sets.

Radioactive Decay Series: Introduction

Radioactive decay series describe the decay of different discrete radioactive decay products as a chained series of transformations.

Learning Objectives

Describe importance of radioactive decay series for decay process.

Key Takeaways

Key Points

• Most radioactive elements do not decay directly to a stable state; rather, they undergo a series of decays until eventually a stable isotope is reached.
• Half-lives of radioisotopes range from nearly nonexistent spans of time to as much as 1019 years or more.
• The intermediate stages of radioactive decay series often emit more radioactivity than the original radioisotope.

Key Terms

• half-life: the time required for half of the nuclei in a sample of a specific isotope to undergo radioactive decay
• radioisotope: a radioactive isotope of an element
• decay: to change by undergoing fission, by emitting radiation, or by capturing or losing one or more electrons

Radioactive decay series, or decay chains, describe the radioactive decay of different discrete radioactive decay products as a chained series of transformations. Most radioactive elements do not decay directly to a stable state; rather, they undergo a series of decays until eventually a stable isotope is reached.

Radioactive Decay Series Diagram: This diagram provides examples of four decay series: thorium (in blue), radium (in red), actinium (in green), and neptunium (in purple).

Decay stages are referred to by their relationship to previous or subsequent stages. A parent isotope is one that undergoes decay to form a daughter isotope. The daughter isotope may be stable, or it may itself decay to form a daughter isotope of its own. The daughter of a daughter isotope is sometimes called a granddaughter isotope.
The time it takes for a single parent atom to decay to an atom of its daughter isotope can vary widely, not only for different parent-daughter chains, but also for identical pairings of parent and daughter isotopes. While the decay of a single atom occurs spontaneously, the decay of an initial population of identical atoms over time, $\text{t}$ , follows a decaying exponential distribution, ${\text{e}}^{-\text{t}}$ , where $\lambda$ is called the decay constant. Because of this exponential nature, one of the properties of an isotope is its half-life, the time by which half of an initial number of identical parent radioisotopes have decayed to their daughters. Half-lives have been determined in laboratories for thousands of radioisotopes (radionuclides). These half-lives can range from nearly nonexistent spans of time to as much as ${10}^{19}$ years or more.
The intermediate stages often emit more radioactivity than the original radioisotope. When equilibrium is achieved, a granddaughter isotope is present in proportion to its half-life. But, since its activity is inversely proportional to its half-life, any nuclide in the decay chain finally contributes as much as the head of the chain. For example, natural uranium is not significantly radioactive, but pitchblende, a uranium ore, is 13 times more radioactive because of the radium and other daughter isotopes it contains. Not only are unstable radium isotopes significant radioactivity emitters, but as the next stage in the decay chain they also generate radon, a heavy, inert, naturally occurring radioactive gas. Rock containing thorium and/or uranium (such as some granites) emits radon gas, which can accumulate in enclosed places such as basements or underground mines. Radon exposure is considered the leading cause of lung cancer in non-smokers.

Alpha Decay

In alpha decay an atomic nucleus emits an alpha particle and transforms into an atom with smaller mass (by four) and atomic number (by two).

Learning Objectives

Describe the process, penetration power, and effects of alpha radiation

Key Takeaways

Key Points

• An alpha particle is the same as a helium-4 nucleus, which has mass number 4 and atomic number 2.
• Because of their relatively large mass, +2 electric charge, and relatively low velocity, alpha particles are very likely to interact with other atoms and lose their energy, so their forward motion is effectively stopped within a few centimeters of air.
• Most of the helium produced on Earth (approximately 99 percent of it) is the result of the alpha decay of underground deposits of minerals containing uranium or thorium.

Key Terms

• alpha particle: A positively charged nucleus of a helium-4 atom (consisting of two protons and two neutrons), emitted as a consequence of radioactivity; α-particle.
• radioactive decay: any of several processes by which unstable nuclei emit subatomic particles and/or ionizing radiation and disintegrate into one or more smaller nuclei

Alpha decay is a type of radioactive decay in which an atomic nucleus emits an alpha particle that consists of two protons and two neutrons, as shown in. As the result of this process, the parent atom transforms (“decays”) into a new atom with a mass number smaller by four and an atomic number smaller by two.

Alpha Decay: Alpha decay is one type of radioactive decay. An atomic nucleus emits an alpha particle and thereby transforms (“decays”) into an atom with a mass number smaller by four and an atomic number smaller by two. Many other types of decay are possible.

For example: 238U → 234Th + α
Because an alpha particle is the same as a helium-4 nucleus, which has mass number 4 and atomic number 2, this can also be written as:
238
92U → 234
90Th + 4
2He
The alpha particle also has charge +2, but the charge is usually not written in nuclear equations, which describe nuclear reactions without considering the electrons. This convention is not meant to imply that the nuclei necessarily occur in neutral atoms.
Alpha decay is by far the most common form of cluster decay, in which the parent atom ejects a defined daughter collection of nucleons, leaving another defined product behind (in nuclear fission, a number of different pairs of daughters of approximately equal size are formed). Alpha decay is the most common cluster decay because of the combined extremely high binding energy and relatively small mass of the helium-4 product nucleus (the alpha particle).
Alpha decay typically occurs in the heaviest nuclides. In theory it can occur only in nuclei somewhat heavier than nickel (element 28), in which overall binding energy per nucleon is no longer a minimum and the nuclides are therefore unstable toward spontaneous fission-type processes. The lightest known alpha emitters are the lightest isotopes (mass numbers 106-110) of tellurium (element 52).
Alpha particles have a typical kinetic energy of 5 MeV (approximately 0.13 percent of their total energy, i.e., 110 TJ/kg) and a speed of 15,000 km/s. This corresponds to a speed of around 0.05 c. There is surprisingly small variation in this energy, due to the heavy dependence of the half-life of this process on the energy produced.
Because of their relatively large mass, +2 electric charge, and relatively low velocity, alpha particles are very likely to interact with other atoms and lose their energy, so their forward motion is effectively stopped within a few centimeters of air.
Most of the helium produced on Earth (approximately 99 percent of it) is the result of the alpha decay of underground deposits of minerals containing uranium or thorium. The helium is brought to the surface as a byproduct of natural gas production.

Beta Decay

Beta decay is a type of radioactive decay in which a beta particle (an electron or a positron) is emitted from an atomic nucleus.

Learning Objectives

Explain difference between beta minus and beta plus decays.

Key Takeaways

Key Points

• There are two types of beta decay: beta minus, which leads to an electron emission, and beta plus, which leads to a positron emission.
• Beta decay allows the atom to obtain the optimal ratio of protons and neutrons.
• Beta decay processes transmute one chemical element into another.

Key Terms

• beta decay: a nuclear reaction in which a beta particle (electron or positron) is emitted
• positron: The antimatter equivalent of an electron, having the same mass but a positive charge.
• transmutation: the transformation of one element into another by a nuclear reaction

Beta decay is a type of radioactive decay in which a beta particle (an electron or a positron) is emitted from an atomic nucleus, as shown in. Beta decay is a process that allows the atom to obtain the optimal ratio of protons and neutrons.

Beta Decay: β decay in an atomic nucleus (the accompanying antineutrino is omitted). The inset shows beta decay of a free neutron

There are two types of beta decay. Beta minus (β) leads to an electron emission (e⁻); beta plus (β+) leads to a positron emission (e⁺). In electron emission an electron antineutrino is also emitted, while positron emission is accompanied by an electron neutrino. Beta decay is mediated by the weak force.
Emitted beta particles have a continuous kinetic energy spectrum, ranging from 0 to the maximal available energy (Q), that depends on the parent and daughter nuclear states that participate in the decay. The continuous energy spectra of beta particles occur because Q is shared between a beta particle and a neutrino. A typical Q is around 1 MeV, but it can range from a few keV to a several tens of MeV. Since the rest mass energy of the electron is 511 keV, the most energetic beta particles are ultrarelativistic, with speeds very close to the speed of light.
Since the proton and neutron are part of an atomic nucleus, beta decay processes result in transmutation of one chemical element into another. For example:
137Cs $\to$ 137Ba + e⁻
11Na $\to$ 10Ne + e⁺
Beta decay does not change the number of nucleons, A, in the nucleus; it changes only its charge, Z. Therefore the set of all nuclides with the same A can be introduced; these isobaric nuclides may turn into each other via beta decay.
A beta-stable nucleus may undergo other kinds of radioactive decay (for example, alpha decay). In nature, most isotopes are beta-stable, but there exist a few exceptions with half-lives so long that they have not had enough time to decay since the moment of their nucleosynthesis. One example is the odd-proton odd-neutron nuclide 40 K, which undergoes both types of beta decay with a half-life of 1.277 ·10⁹ years.

Beta Decay 1/2: In this video I introduce Beta decay and discuss it from an basic level to a perhaps second or third year University level.

Beta Decay 2/2: In this video I introduce Beta decay and discuss it from an basic level to a perhaps second or third year University level.

Gamma Decay

Gamma decay is a process of emission of gamma rays that accompanies other forms of radioactive decay, such as alpha and beta decay.

Learning Objectives

Explain relationship between gamma decay and other forms of nuclear decay.

Key Takeaways

Key Points

• Gamma decay accompanies other forms of decay, such as alpha and beta decay; gamma rays are produced after the other types of decay occur.
• Although emission of gamma ray is a nearly instantaneous process, it can involve intermediate metastable excited states of the nuclei.
• Gamma rays are generally the most energetic form of electromagnetic radiation.

Key Terms

• electromagnetic radiation: radiation (quantized as photons) consisting of oscillating electric and magnetic fields oriented perpendicularly to each other, moving through space
• gamma ray: A very high frequency (and therefore very high energy) electromagnetic radiation emitted as a consequence of radioactivity.

Gamma radiation, also known as gamma rays and denoted as $\gamma$ , is electromagnetic radiation of high frequency and therefore high energy. Gamma rays typically have frequencies above 10 exahertz ($>{10}^{19}$ Hz) and therefore have energies above 100 keV and wavelengths less than 10 picometers (less than the diameter of an atom). However, this is not a strict definition; rather, it is a rule-of-thumb description for natural processes. Gamma rays from radioactive decay are defined as gamma rays no matter what their energy, so there is no lower limit to gamma energy derived from radioactive decay. Gamma decay commonly produces energies of a few hundred keV and usually less than 10 MeV.

Cobalt-60 Decay Scheme: Path of decay of Co-60 to Ni-60. Excited levels for Ni-60 that drop to ground state via emission of gamma rays are indicated

Gamma decay accompanies other forms of decay, such as alpha and beta decay; gamma rays are produced after the other types of decay occur. When a nucleus emits an α or β particle, the daughter nucleus is usually left in an excited state. It can then move to a lower energy state by emitting a gamma ray, in much the same way that an atomic electron can jump to a lower energy state by emitting a photon. For example, cobalt-60 decays to excited nickel-60 by beta decay through emission of an electron of 0.31 MeV. Next, the excited nickel-60 drops down to the ground state by emitting two gamma rays in succession (1.17 MeV, then 1.33 MeV), as shown in. Emission of a gamma ray from an excited nuclear state typically requires only ${10}^{-12}$ seconds: it is nearly instantaneous. Gamma decay from excited states may also follow nuclear reactions such as neutron capture, nuclear fission, or nuclear fusion.
In certain cases, the excited nuclear state following the emission of a beta particle may be more stable than average; in these cases it is termed a metastable excited state if its decay is 100 to 1000 times longer than the average ${10}^{-12}$ seconds. Such nuclei have half-lives that are easily measurable; these are termed nuclear isomers. Some nuclear isomers are able to stay in their excited state for minutes, hours, or days, or occasionally far longer, before emitting a gamma ray. This phenomenon is called isomeric transition. The process of isomeric transition is therefore similar to any gamma emission; it differs only in that it involves the intermediate metastable excited states of the nuclei.

Half-Life and Rate of Decay; Carbon-14 Dating

Carbon-14 dating is a radiometric dating method that uses the radioisotope carbon-14 (14C) to estimate the age of object.

Learning Objectives

Identify the age of materials that can be approximately determined using radiocarbon dating

Key Takeaways

Key Points

• Carbon-14 dating can be used to estimate the age of carbon-bearing materials up to about 58,000 to 62,000 years old.
• The carbon-14 isotope would vanish from Earth’s atmosphere in less than a million years were it not for the constant influx of cosmic rays interacting with atmospheric nitrogen.
• One of the most frequent uses of radiocarbon dating is to estimate the age of organic remains from archaeological sites.

Key Terms

• radioisotope: a radioactive isotope of an element
• radiometric dating: Radiometric dating is a technique used to date objects based on a comparison between the observed abundance of a naturally occurring radioactive isotope and its decay products using known decay rates.
• carbon-14: carbon-14 is a radioactive isotope of carbon with a nucleus containing 6 protons and 8 neutrons.

Radiocarbon dating (usually referred to simply as carbon-14 dating) is a radiometric dating method. It uses the naturally occurring radioisotope carbon-14 (14C) to estimate the age of carbon-bearing materials up to about 58,000 to 62,000 years old.
Carbon has two stable, nonradioactive isotopes: carbon-12 (12C) and carbon-13 (13C). There are also trace amounts of the unstable radioisotope carbon-14 (14C) on Earth. Carbon-14 has a relatively short half-life of 5,730 years, meaning that the fraction of carbon-14 in a sample is halved over the course of 5,730 years due to radioactive decay to nitrogen-14. The carbon-14 isotope would vanish from Earth’s atmosphere in less than a million years were it not for the constant influx of cosmic rays interacting with molecules of nitrogen (N₂) and single nitrogen atoms (N) in the stratosphere. Both processes of formation and decay of carbon-14 are shown in.

Formation and Decay of Carbon-14: Diagram of the formation of carbon-14 (1), the decay of carbon-14 (2), and equations describing the carbon-12:carbon-14 ratio in living and dead organisms

When plants fix atmospheric carbon dioxide (CO₂) into organic compounds during photosynthesis, the resulting fraction of the isotope 14C in the plant tissue will match the fraction of the isotope in the atmosphere. After plants die or are consumed by other organisms, the incorporation of all carbon isotopes, including 14C, stops. Thereafter, the concentration (fraction) of 14C declines at a fixed exponential rate due to the radioactive decay of 14C. (An equation describing this process is shown in. ) Comparing the remaining 14C fraction of a sample to that expected from atmospheric 14C allows us to estimate the age of the sample.
Raw (i.e., uncalibrated) radiocarbon ages are usually reported in radiocarbon years “Before Present” (BP), with “present” defined as CE 1950. Such raw ages can be calibrated to give calendar dates. One of the most frequent uses of radiocarbon dating is to estimate the age of organic remains from archaeological sites.
The technique of radiocarbon dating was developed by Willard Libby and his colleagues at the University of Chicago in 1949. Emilio Segrè asserted in his autobiography that Enrico Fermi suggested the concept to Libby at a seminar in Chicago that year. Libby estimated that the steady-state radioactivity concentration of exchangeable carbon-14 would be about 14 disintegrations per minute (dpm) per gram. In 1960, Libby was awarded the Nobel Prize in chemistry for this work. He demonstrated the accuracy of radiocarbon dating by accurately estimating the age of wood from a series of samples for which the age was known, including an ancient Egyptian royal barge dating from 1850 BCE.

Half-life: Describes radioactive half life and how to do some simple calculations using half life.

Calculations Involving Half-Life and Decay-Rates

The half-life of a radionuclide is the time taken for half the radionuclide’s atoms to decay.

Learning Objectives

Explain what is a half-life of a radionuclide.

Key Takeaways

Key Points

• The half-life is related to the decay constant as follows: ${\text{t}}_{1/2}=\text{ln}2/\lambda$ .
• The relationship between the half-life and the decay constant shows that highly radioactive substances are quickly spent while those that radiate weakly endure longer.
• Half-lives of known radionuclides vary widely, from more than 10¹⁹ years, such as for the very nearly stable nuclide 209 Bi, to 10^-23 seconds for highly unstable ones.

Key Terms

• half-life: the time required for half of the nuclei in a sample of a specific isotope to undergo radioactive decay
• radionuclide: A radionuclide is an atom with an unstable nucleus, characterized by excess energy available to be imparted either to a newly created radiation particle within the nucleus or via internal conversion.

The half-life of a radionuclide is the time taken for half of the radionuclide’s atoms to decay. Taking $\lambda$  to be the decay rate (number of disintegrations per unit time), and $\tau$  the average lifetime of an atom before it decays, we have:
$\text{N}\left(\text{t}\right)={\text{N}}_0{\text{e}}^{-\lambda \text{t}}={\text{N}}_0{\text{e}}^{-\text{t}/\tau }$
The half-life is related to the decay constant by substituting the condition $\text{N}={\text{N}}_{\text{o}}/2$  and solving for $\text{t}={\text{t}}_{1/2}$ :
${\text{t}}_{1/2}=\text{ln}2/\lambda =\tau \text{ln}2$
A half-life must not be thought of as the time required for exactly half of the atoms to decay.

Radioactive decay simulation: A simulation of many identical atoms undergoing radioactive decay, starting with four atoms (left) and 400 atoms (right). The number at the top indicates how many half-lives have elapsed

The following figure shows a simulation of many identical atoms undergoing radioactive decay. Note that after one half-life there are not exactly one-half of the atoms remaining; there are only approximately one-half left because of the random variation in the process. However, with more atoms (the boxes on the right), the overall decay is smoother and less random-looking than with fewer atoms (the boxes on the left), in accordance with the law of large numbers.
The relationship between the half-life and the decay constant shows that highly radioactive substances are quickly spent while those that radiate weakly endure longer. Half-lives of known radionuclides vary widely, from more than 10¹⁹ years, such as for the very nearly stable nuclide 209 Bi, to 10⁻²³ seconds for highly unstable ones.
The factor of ln(2) in the above equations results from the fact that the concept of “half-life” is merely a way of selecting a different base other than the natural base e for the lifetime expression. The time constant τ is the e^-1-life, the time until only 1/e remains — about 36.8 percent, rather than the 50 percent in the half-life of a radionuclide. Therefore, τ is longer than t_1/2. The following equation can be shown to be valid:
$\text{N}\left(\text{t}\right)={\text{N}}_0{\text{e}}^{-\text{t}/\tau }={\text{N}}_0{2}^{-\text{t}/{\text{t}}_{1/2}}$
Since radioactive decay is exponential with a constant probability, each process could just as easily be described with a different constant time period that (for example) gave its 1/3-life (how long until only 1/3 is left), or its 1/10-life (how long until only 1/10 is left), and so on. Therefore, the choice of τ and t_1/2 for marker-times is only for convenience and for the sake of uploading convention. These marker-times reflect a fundamental principle only in that they show that the same proportion of a given radioactive substance will decay over any time period you choose.
Mathematically, the nth life for the above situation would be found by the same process shown above — by setting $\text{N}={\text{N}}_0/\text{n}$ and substituting into the decay solution, to obtain:
${\text{t}}_{1/\text{n}}=\frac{\text{lnn}}{\lambda }=\tau \text{lnn}$

Half-life: Part of a series of videos on physics problem-solving. The problems are taken from “The Joy of Physics. ” This one deals with radioactive half-life. The viewer is urged to pause the video at the problem statement and work the problem before watching the rest of the video.

 

Quantum Tunneling and Conservation Laws

Quantum Tunneling

If an object lacks enough energy to pass through a barrier, it is possible for it to “tunnel” through imaginary space to the other side.

Learning Objectives

Identify factors that affect the tunneling probability

Key Takeaways

Key Points

• Quantum tunneling applies to all objects facing any barrier. However, the probability of its occurrence is essentially negligible for macroscopic purposes; it is only ever observed to any appreciable degree on the nanoscale level.
• Quantum tunneling is explained by the imaginary component of the Schrödinger equation. Because the wave function of any object contains an imaginary component, it can exist in imaginary space.
• Tunneling decreases with the increasing mass of the object that must tunnel and with the increasing gap between the object’s energy and the energy of the barrier it must overcome.

Key Terms

• tunneling: the quantum-mechanical passing of a particle through an energy barrier

Imagine throwing a ball at a wall and having it disappear the instant before it makes contact and appear on the other side. The wall remains intact; the ball did not break through it. Believe it or not, there is a finite (if extremely small) probability that this event would occur. This phenomenon is called quantum tunneling.
While the possibility of tunneling is essentially ignorable at macroscopic levels, it occurs regularly on the nanoscale level. Consider, for example, a p-orbital in an atom. Between the two lobes there is a nodal plane. By definition there is precisely 0 probability of finding an electron anywhere along that plane, and because the plane extends infinitely it is impossible for an electron to go around it. Yet, electrons commonly cross from one lobe to the other via quantum tunneling. They never exist in the nodal area (this is forbidden); instead they travel through imaginary space.

P-Orbital: The red and blue lobes represent the volume in which there is a 90 percent probability of finding an electron at any given time if the orbital is occupied.

Imaginary space is not real, but it is explicitly referenced in the time-dependent Schrödinger equation, which has a component of $\text{i}$ (the square root of $-1$ , an imaginary number):
$\text{i}\hslash \frac{\partial }{\partial \text{t}}\Psi =\hat{\text{H}}\Psi$
And because all matter has a wave component (see the topic of wave-particle duality), all matter can in theory exist in imaginary space. But what accounts for the difference in probability of an electron tunneling over a nodal plane and a ball tunneling through a brick wall? The answer is a combination of the tunneling object’s mass ($\text{m}$ ) and energy ($\text{E}$ ) and the energy height (${\text{U}}_0$ ) of the barrier through which it must travel to get to the other side.
When it reaches a barrier it cannot overcome, a particle’s wave function changes from sinusoidal to exponentially diminishing in form. The solution for the Schrödinger equation in such a medium is:
$\Psi ={\text{Ae}}^{-\alpha \text{x}}$
where:
$\alpha =\sqrt{\frac{2\text{m}({\text{U}}_0-\text{E})}{{\text{h}}^2}}$
Therefore, the probability of an object tunneling through a barrier decreases with the object’s increasing mass and with the increasing gap between the energy of the object and the energy of the barrier. And although the wave function never quite reaches 0 (as can be determined from the ${\text{e}}^{-\text{x}}$ functionality), this explains how tunneling is frequent on nanoscale but negligible at the macroscopic level.

Conservation of Nucleon Number and Other Laws

Through radioactive decay, nuclear fusion and nuclear fission, the number of nucleons (sum of protons and neutrons) is always held constant.

Learning Objectives

Define the Law of Conservation of Nuclear Number

Key Takeaways

Key Points

• The law of Conservation of Nuclear Number states that the sum of protons and neutrons among species before and after a nuclear reaction will be the same.
• In radioactive decay, a proton can be converted to a neutron and a neutron can be converted to a proton (beta-decay).
• Nuclear fusion and fission involve the conversion of matter to energy, but the matter that is converted is never a full nucleon.

Key Terms

• fusion: A nuclear reaction in which nuclei combine to form more massive nuclei with the concomitant release of energy.
• fission: The process of splitting the nucleus of an atom into smaller particles; nuclear fission.
• nucleon: One of the subatomic particles of the atomic nucleus (i.e., a proton or a neutron).

In physics and chemistry there are many conservation laws—among them, the Law of Conservation of Nucleon Number, which states that the total number of nucleons (nuclear particles, specifically protons and neutrons) cannot change by any nuclear reaction.

Radioactive Decay

Consider the three modes of decay. In gamma decay, an excited nucleus releases gamma rays, but its proton (Z) and neutron (A-Z) count remain the same:
${}_{\text{ZN}}^{\text{A}}{\to }_{\text{ZN}}^{\text{A}}+\gamma$ .

Nuclear fission of U-235: If U-235 is bombarded with a neutron (light blue small circe), the resulting U-236 produced is unstable and undergoes fission. The resulting elements (shown here as Kr-92 and Ba-141) do not contain as many nucleons as U-236, with the remaining three neutrons being released as high-energy particles, able to bombard another U-235 atom and maintain a chain reaction.

In beta decay, a nucleus releases energy and either an electron or a positron. In the case of an electron being released, atomic mass (A) remains the same as a neutron is converted into a proton, raising atomic number by 1:
${}_{\text{ZN}}^{\text{A}}{\to }_{\text{Z}+1}^{\text{A}}\text{N}+{\text{e}}^{-}+\nu$ .
In the case of a positron being released, atomic mass remains constant as a proton is converted to a neutron, lowering atomic number by 1:
${}_Z^{\text{A}}\text{N}{\to }_{\text{Z}-1}^{\text{A}}\text{N}+{\text{e}}^{+}+\nu$ .
Electron capture has the same effect on the number of protons and neutrons in a nucleus as positron emission.
Alpha decay is the only type of radioactive decay that results in an appreciable change in an atom ‘s atomic mass. However, rather than being destroyed, the two protons and two neutrons an atom loses in alpha decay are released as a helium nucleus.

Nuclear Fission

Chain reactions of nuclear fission release a tremendous amount of energy, but follow the Law of Conservation of Nucleon Number. Consider, for example, the multistep reaction that occurs when a U-235 nucleus accepts a neutron, as in:
${}_0^1\text{n}{+}_{92}^{235}\text{U}{\to }_{92}^{236}\text{U}{\to }_{56}^{144}\text{Ba}{+}_{36}^{89}\text{Kr}+3_0^1\text{n}+\gamma$ .
In each step, the total atomic mass of all species is a constant value of 236. This is the same with all fission reactions.

Nuclear Fusion

Finally, nuclear fusion follows the Law of Conservation of Nucleon Number. Consider the fusion of deuterium and tritium (both hydrogen isotopes):
${}_1^2\text{H}{+}_1^3\text{H}{\to }_2^4\text{He}{+}_0^1\text{n}$ .
It is well understood that the tremendous amounts of energy released by nuclear fission and fusion can be attributed to the conversion of mass to energy. However, the mass that is converted to energy is rather small compared to any sample, and never includes the conversion of a proton or neutron to energy. Thus, the number of nucleons before and after fission and fusion is always constant.

 

Applications of Nuclear Physics

Medical Imaging and Diagnostics

Radiation therapy uses ionizing radiation to treat conditions such as hyperthyroidism, cancer, and blood disorders.

Key Takeaways

KEY POINTS

• Ionizing radiation works by damaging the DNA of exposed tissue, leading to cellular death.
• In external beam radiotherapy, shaped radiation beams are aimed from several angles of exposure to intersect at the tumor, providing a much larger absorbed dose there than in the surrounding, healthy tissue.
• In brachytherapy, a therapeutic radioisotope is injected into the body to chemically localize to the tissue that requires destruction.

KEY TERMS

• external beam therapy: Radiotherapy that directs the radiation at the tumour from outside the body.
• ionizing radiation: high-energy radiation that is capable of causing ionization in substances through which it passes; also includes high-energy particles
• brachytherapy: Radiotherapy using radioactive sources positioned within (or close to) the treatment volume.

Example

The nuclear medicine whole body bone scan is generally used in evaluations of various bone related pathology, such as for bone pain, stress fracture, nonmalignant bone lesions, bone infections, or the spread of cancer to the bone.

Radiation therapy involves the application of ionizing radiation to treat conditions such as hyperthyroidism, thyroid cancer, and blood disorders. Radiation therapy is particularly effective as a treatment of a number of types of cancer if they are localized to one area of the body. It may also be used as part of curative therapy, to prevent tumor recurrence after surgery, or to remove a primary malignant tumor. Radiation therapy is synergistic with chemotherapy and has been used before, during, and after chemotherapy in susceptible cancers.
Ionizing radiation works by damaging the DNA of exposed tissue, leading to cellular death. When external beam therapy is used, shaped radiation beams are aimed from several angles of exposure to intersect at the tumor, providing a much larger absorbed dose there than in the surrounding, healthy tissue.

External Beam Therapy: Radiation therapy of the pelvis. Lasers and a mold under the legs are used for precise positioning

Brachytherapy is another form of radiation therapy, in which a therapeutic radioisotope is injected into the body to chemically localize to the tissue that requires destruction . A key feature of brachytherapy is that the irradiation affects only a very localized area around the radiation sources. Exposure to radiation of healthy tissues further away from the sources is therefore reduced in this technique.
Radiation therapy is in itself painless. Many low-dose palliative treatments (for example, radiation therapy targeting bony metastases) cause minimal or no side effects, although short-term pain flare-ups can be experienced in the days following treatment due to edemas compressing nerves in the treated area. Higher doses can cause varying side effects during treatment (acute), in the months or years following treatment (long-term), or after re-treatment (cumulative). The nature, severity, and longevity of side effects depend on the organs that receive the radiation, the treatment itself (type of radiation, dose, fractionation, concurrent chemotherapy), and the individual patient.

Dosimetry

Radiation dosimetry is the measurement and calculation of the absorbed dose resulting from the exposure to ionizing radiation.

Learning Objectives

Explain difference between absorbed dose and dose equivalent.

Key Takeaways

KEY POINTS

• There are several ways of measuring doses of ionizing radiation: personal dosimeters, ionization chambers, and internal dosimetry.
• The distinction between absorbed dose (Gy/rad) and dose equivalent (Sv/rem) is based upon the biological effects.
• Dose is a measure of deposited dose and therefore can never decrease: removal of a radioactive source can reduce only the rate of increase of absorbed dose — never the total absorbed dose.

KEY TERMS

• diode: an electronic device that allows current to flow in one direction only; a valve
• ionizing radiation: high-energy radiation that is capable of causing ionization in substances through which it passes; also includes high-energy particles
• dosimeter: A dosimeter is a device used to measure a dose of ionizing radiation. These normally take the form of either optically stimulated luminescence (OSL), photographic-film, thermoluminescent (TLD), or electronic personal dosimeters (PDM).

Radiation dosimetry is the measurement and calculation of the absorbed dose in matter and tissue resulting from the exposure to indirect and direct ionizing radiation.

Measuring Radiation

There are several ways of measuring the dose of ionizing radiation. Workers who come in contact with radioactive substances or who may be exposed to radiation routinely carry personal dosimeters . In the United States, these dosimeters usually contain materials that can be used in thermoluminescent dosimetry or optically stimulated luminescence. Outside the United States, the most widely used type of personal dosimeter is the film badge dosimeter, which uses photographic emulsions that are sensitive to ionizing radiation. The equipment used in radiotherapy (a linear particle accelerator in external beam therapy) is routinely calibrated using ionization chambers or the new and more accurate diode technology. Internal dosimetry is used to evaluate the intake of particles inside a human being.

Ionization Chamber: This ionization chamber was used in the South Atlantic Anomaly Probe project.

Personal Radiation Dosimeter: A physician wearing a personal radiation dosimeter

Dose is reported in grays (Gy) for absorbed doses or sieverts (Sv) for dose equivalents, where 1 Gy or 1 Sv is equal to 1 joule per kilogram. Non-SI units are still prevalent as well: absorbed dose is often reported in rads and dose equivalent in rems. By definition, 1 Gy = 100 rad, and 1 Sv = 100 rem.

Biological Effects

The distinction between absorbed dose (Gy/rad) and dose equivalent (Sv/rem) is based upon the biological effects. The weighting factor (wr) and tissue/organ weighting factor (WT) have been established. They compare the relative biological effects of various types of radiation and the susceptibility of different organs.
The weighting factor for the whole body is 1, such that 1 Gy of radiation delivered to the whole body is equal to one sievert. Therefore, the WT for all organs in the whole body must sum to 1.
By definition, X-rays and gamma rays have a wr of unity, such that 1 Gy = 1 Sv (for whole-body irradiation). Values of wr are as high as 20 for alpha particles and neutrons. That is to say, for the same absorbed dose in Gy, alpha particles are 20 times as biologically potent as x-rays or gamma rays.
Dose is a measure of deposited dose and therefore can never decrease: removal of a radioactive source can reduce only the rate of increase of absorbed dose — never the total absorbed dose.

Biological Effects of Radiation

Ionizing radiation is generally harmful, even potentially lethal, to living organisms.

Learning Objectives

Describe effects of ionizing radiation on living organisms.

Key Takeaways

KEY POINTS

• The effects of ionizing radiation on human health are separated into stochastic effects (the probability of occurrence increases with dose) and deterministic effects (they reliably occur above a threshold dose, and their severity increases with dose).
• Quantitative data on the effects of ionizing radiation on human health are relatively limited compared to other medical conditions because of the low number of cases to date and because of the stochastic nature of some of the effects.
• Two pathways (external and internal) of exposure to ionizing radiation exist.

KEY TERMS

ionizing radiation: high-energy radiation that is capable of causing ionization in substances through which it passes; also includes high-energy particles

Example

The Radium Girls were female factory workers who contracted radiation poisoning from painting watch dials with glow-in-the-dark paint at the United States Radium factory in Orange, New Jersey around 1917. The women, who had been told the paint was harmless, ingested deadly amounts of radium by licking their paintbrushes to give them a fine point; some also painted their fingernails and teeth with the glowing substance.

Ionizing radiation is generally harmful, even potentially lethal, to living organisms. Although radiation was discovered in the late 19th century, the dangers of radioactivity and of radiation were not immediately recognized. The acute effects of radiation were first observed in the use of x-rays when Wilhelm Röntgen intentionally subjected his fingers to x-rays in 1895. The genetic effects of radiation, including the effects on cancer risk, were recognized much later. In 1927, Hermann Joseph Muller published research showing genetic effects.
Some effects of ionizing radiation on human health are stochastic, meaning that their probability of occurrence increases with dose, while the severity is independent of dose. Radiation-induced cancer, teratogenesis, cognitive decline, and heart disease are all examples of stochastic effects. Other conditions, such as radiation burns, acute radiation syndrome, chronic radiation syndrome, and radiation-induced thyroiditis are deterministic, meaning they reliably occur above a threshold dose and their severity increases with dose. Deterministic effects are not necessarily more or less serious than stochastic effects; either can ultimately lead to damage ranging from a temporary nuisance to death.

Radium Girls: Radium dial painters working in a factory

Quantitative data on the effects of ionizing radiation on human health are relatively limited compared to other medical conditions because of the low number of cases to date and because of the stochastic nature of some of the effects. Stochastic effects can only be measured through large epidemiological studies in which enough data have been collected to remove confounding factors such as smoking habits and other lifestyle factors. The richest source of high-quality data is the study of Japanese atomic bomb survivors.
Two pathways of exposure to ionizing radiation exist. In the case of external exposure, the radioactive source is outside (and remains outside) the exposed organism. Examples of external exposure include a nuclear worker whose hands have been dirtied with radioactive dust or a person who places a sealed radioactive source in his pocket. External exposure is relatively easy to estimate, and the irradiated organism does not become radioactive, except if the radiation is an intense neutron beam that causes activation. In the case of internal exposure, the radioactive material enters the organism, and the radioactive atoms become incorporated into the organism. This can occur through inhalation, ingestion, or injection. Examples of internal exposure include potassium-40 present within a normal person or the ingestion of a soluble radioactive substance, such as strontium-89 in cows’ milk. When radioactive compounds enter the human body, the effects are different from those resulting from exposure to an external radiation source. Especially in the case of alpha radiation, which normally does not penetrate the skin, the exposure can be much more damaging after ingestion or inhalation.

Therapeutic Uses of Radiation

Radiation therapy uses ionizing radiation to treat conditions such as hyperthyroidism, cancer, and blood disorders.

Learning Objectives

Explain difference between external beam radiotherapy and brachytherapy.

Key Takeaways

KEY POINTS

• Ionizing radiation works by damaging the DNA of exposed tissue, leading to cellular death.
• In external beam radiotherapy, shaped radiation beams are aimed from several angles of exposure to intersect at the tumor, providing a much larger absorbed dose there than in the surrounding, healthy tissue.
• In brachytherapy, a therapeutic radioisotope is injected into the body to chemically localize to the tissue that requires destruction.

KEY TERMS

• ionizing radiation: high-energy radiation that is capable of causing ionization in substances through which it passes; also includes high-energy particles
• external beam therapy: Radiotherapy that directs the radiation at the tumour from outside the body.
• brachytherapy: Radiotherapy using radioactive sources positioned within (or close to) the treatment volume.

Radiation therapy involves the application of ionizing radiation to treat conditions such as hyperthyroidism, thyroid cancer, and blood disorders. Radiation therapy is particularly effective as a treatment of a number of types of cancer if they are localized to one area of the body. It may also be used as part of curative therapy, to prevent tumor recurrence after surgery, or to remove a primary malignant tumor. Radiation therapy is synergistic with chemotherapy and has been used before, during, and after chemotherapy in susceptible cancers.
Ionizing radiation works by damaging the DNA of exposed tissue, leading to cellular death. When external beam therapy is used, shaped radiation beams are aimed from several angles of exposure to intersect at the tumor, providing a much larger absorbed dose there than in the surrounding, healthy tissue .

External Beam Therapy:  Radiation therapy of the pelvis. Lasers and a mold under the legs are used for precise positioning

Brachytherapy is another form of radiation therapy, in which a therapeutic radioisotope is injected into the body to chemically localize to the tissue that requires destruction . A key feature of brachytherapy is that the irradiation affects only a very localized area around the radiation sources. Exposure to radiation of healthy tissues further away from the sources is therefore reduced in this technique.

Clinical Applications of Brachytherapy: Body sites in which brachytherapy can be used to treat cancer

Radiation therapy is in itself painless. Many low-dose palliative treatments (for example, radiation therapy targeting bony metastases) cause minimal or no side effects, although short-term pain flare-ups can be experienced in the days following treatment due to edemas compressing nerves in the treated area. Higher doses can cause varying side effects during treatment (acute), in the months or years following treatment (long-term), or after re-treatment (cumulative). The nature, severity, and longevity of side effects depend on the organs that receive the radiation, the treatment itself (type of radiation, dose, fractionation, concurrent chemotherapy), and the individual patient.

Radiation from Food

Food irradiation is a process of treating a food to a specific dosage of ionizing radiation for a predefined length of time.

Learning Objectives

Explain how food irradiation is performed, commenting on its purpose and safety

Key Takeaways

KEY POINTS

• Food irradiation kills some of the microorganisms, bacteria, viruses, and insects found in food. It prolongs shelf-life in cases where pathogenic spoilage is the limiting factor.
• Food irradiation using cobalt-60 is the preferred method by most processors.
• Irradiated food does not become radioactive, since the particles that transmit radiation are not themselves radioactive.

KEY TERMS

• gamma ray: A very high frequency (and therefore very high energy) electromagnetic radiation emitted as a consequence of radioactivity.
• x-ray: Short-wavelength electromagnetic radiation usually produced by bombarding a metal target in a vacuum. Used to create images of the internal structure of objects; this is possible because x-rays pass through most objects and can expose photographic film
• ionizing radiation: high-energy radiation that is capable of causing ionization in substances through which it passes; also includes high-energy particles

Food irradiation is a process of treating a food to a specific dosage of ionizing radiation for a predefined length of time. This process slows or halts spoilage that is due to the growth of pathogens. Food irradiation is currently permitted by over 50 countries, and the volume of food treated is estimated to exceed 500,000 metric tons annually worldwide. Irradiated food is sold in regular stores, often in specially marked packages .

Radura Logo: The Radura logo, required by U.S. Food and Drug Administration regulations to show a food has been treated with ionizing radiation

By irradiating food, depending on the dose, some or all of the microorganisms, bacteria, viruses, and insects present are killed. This prolongs the shelf-life of the food in cases where pathogenic spoilage is the limiting factor. Some foods, e.g., herbs and spices, are irradiated at sufficient doses (five kilograys or more) to reduce the microbial counts by several orders of magnitude. Such ingredients do not carry spoilage or pathogen microorganisms into the final product. It has also been shown that irradiation can delay the ripening of fruits and the sprouting of vegetables.
Food irradiation using cobalt-60 is the preferred method by most processors. This is because the deep penetration of gamma rays allows for the treatment of entire industrial pallets or totes at once, which reduces the need for material handling. A pallet or tote is typically exposed for several minutes to several hours, depending on the dose. Radioactive material must be monitored and carefully stored to shield workers and the environment from its gamma rays. During operation this is achieved using concrete shields. With most designs the radioisotope can be lowered into a water-filled source storage pool to allow maintenance personnel to enter the radiation shield. In this mode the water in the pool absorbs the radiation.
X-ray irradiators are considered an alternative to isotope-based irradiation systems. X-rays are generated by colliding accelerated electrons with a dense material (the target), such as tantalum or tungsten, in a process known as bremsstrahlung-conversion. X-ray irradiators are scalable and have deep penetration comparable to Co-60, with the added benefit that the electronic source stops radiating when switched off. They also permit dose uniformity, but these systems generally have low energetic efficiency during the conversion of electron energy to photon radiation, so they require much more electrical energy than other systems. X-ray systems also rely on concrete shields to protect the environment and workers from radiation.
Irradiated food does not become radioactive, since the particles that transmit radiation are not themselves radioactive. Still, there is some controversy in the application of irradiation due to its novelty, the association with the nuclear industry, and the potential for the chemical changes to be different than the chemical changes due to heating food (since ionizing radiation produces a higher energy transfer per collision than conventional radiant heat).

Tracers

A radioactive tracer is a chemical compound in which one or more atoms have been replaced by a radioisotope.

Learning Objectives

Explain structure and use of radioactive tracers

Key Takeaways

KEY POINTS

• Radioactive tracers are used to explore the mechanism of chemical reactions by tracing the path that the radioisotope follows from reactants to products.
• The radioactive isotope can be present in low concentration and its presence still detected by sensitive radiation detectors.
• All the commonly used radioisotopes have short half-lives, do not occur in nature, and are produced through nuclear reactions.

KEY TERMS

• radioactive tracer: a radioactive isotope that, when injected into a chemically similar substance, or artificially attached to a biological or physical system, can be traced by radiation detection devices
• isotope: any of two or more forms of an element where the atoms have the same number of protons but a different number of neutrons within their nuclei. As a consequence, atoms for the same isotope will have the same atomic number but different mass numbers (atomic weights)
• radioactive decay: any of several processes by which unstable nuclei emit subatomic particles and/or ionizing radiation and disintegrate into one or more smaller nuclei

A radioactive tracer is a chemical compound in which one or more atoms have been replaced by a radioisotope. By virtue of its consequent radioactive decay, this compound can be used to explore the mechanism of chemical reactions by tracing the path that the radioisotope follows from reactants to products.
The underlying principle in the creation of a radioactive tracer is that an atom in a chemical compound is replaced by another atom of the same chemical element. In a tracer, this substituting atom is a radioactive isotope. This process is often called radioactive labeling. Radioactive decay is much more energetic than chemical reactions. Therefore, the radioactive isotope can be present in low concentration and its presence still detected by sensitive radiation detectors such as Geiger counters and scintillation counters.

Geiger Counter: Image of a Geiger counter with pancake-type probe

There are two main ways in which radioactive tracers are used:
When a labeled chemical compound undergoes chemical reactions, one or more of the products will contain the radioactive label. Analysis of what happens to the radioactive isotope provides detailed information about the mechanism of the chemical reaction.
A radioactive compound can be introduced into a living organism. The radio-isotope provides a way to build an image showing how that compound and its reaction products are distributed around the organism.
All the commonly used radioisotopes (Tritium (${}^3\text{H}$ ), ${}^{11}\text{C}$ , ${}^{13}\text{N}$ , ${}^{15}\text{O}$ , ${}^{18}\text{F}$ , ${}^{32}\text{P}$ , ${}^{35}\text{S}$ , ${}^{99\text{m}}\text{Tc}$ , and ${}^{123}\text{I}$ ) have short half-lives. They do not occur in nature and are produced through nuclear reactions.

Iodine; 123 Radioisotope: Lead container containing iodine-123 radioisotope

Nuclear Fusion

In nuclear fusion two or more atomic nuclei collide at very high speed and join, forming a new nucleus.

Learning Objectives

Analyze possibility of the use of nuclear fusion for the production of electricity.

Key Takeaways

KEY POINTS

• The fusion of lighter elements releases energy.
• Matter is not conserved during fusion reactions.
• Fusion reactions power the stars and produce virtually all elements in a process called nucleosynthesis.

KEY TERMS

• nucleosynthesis: any of several processes that lead to the synthesis of heavier atomic nuclei
• fusion: A nuclear reaction in which nuclei combine to form more massive nuclei with the concomitant release of energy.

Example

The sun is a main-sequence star and therefore generates its energy through nuclear fusion of hydrogen nuclei into helium. In its core, the sun fuses 620 million metric tons of hydrogen each second.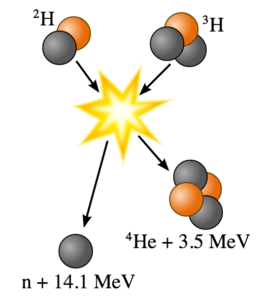

Nuclear fusion is a nuclear reaction in which two or more atomic nuclei collide at very high speed and join to form a new type of atomic nucleus. During this process, matter is not conserved because some of the mass of the fusing nuclei is converted into energy.

Fusion of Deuterium with Tritium:  Fusion of deuterium with tritium creating helium-4, freeing a neutron, and releasing 17.59 MeV of energy; some mass changes form to appear as the kinetic energy of the products

Fission and Fusion
Describes the difference between fission and fusion
Fusion reactions of light elements power the stars and produce virtually all elements in a process called nucleosynthesis. The fusion of lighter elements in stars releases energy and mass. For example, in the fusion of two hydrogen nuclei to form helium, 0.7 percent of the mass is carried away from the system in the form of kinetic energy or other forms of energy (such as electromagnetic radiation).
It takes considerable energy to force nuclei to fuse, even nuclei of the lightest element, hydrogen. This is because all nuclei have a positive charge due to their protons, and since like charges repel, nuclei strongly resist being put close together. Accelerated to high speeds, they can overcome this electrostatic repulsion and be forced close enough for the attractive nuclear force to be sufficiently strong to achieve fusion. The fusion of lighter nuclei, which creates a heavier nucleus and often a free neutron or proton, generally releases more energy than it takes to force the nuclei together. This is an exothermic process that can produce self-sustaining reactions.
Research into controlled fusion, with the aim of producing fusion power for the production of electricity, has been conducted for over 60 years. It has been accompanied by extreme scientific and technological difficulties, but it has resulted in progress. At present, controlled fusion reactions have been unable to produce self-sustaining controlled fusion reactions. Researchers are working on a reactor that theoretically will deliver 10 times more fusion energy than the amount needed to heat up plasma to required temperatures. Workable designs of this reactor were originally scheduled to be operational in 2018; however, this has been delayed, and a new date has not been released.

Nuclear Fission in Reactors

Nuclear reactors convert the thermal energy released from nuclear fission into electricity.

Learning Objectives

Explain how nuclear chain reactions can be controlled.

Key Takeaways

KEY POINTS

• Nuclear fission is a nuclear reaction in which the nucleus of an atom splits into smaller parts, releasing a very large amount of energy.
• Nuclear chain reactions can be controlled using neutron poisons and neutron moderators.
• Although the nuclear power industry has improved the safety and performance of reactors and has proposed new, safer reactor designs, there is no guarantee that serious nuclear accidents will not occur.

KEY TERMS

• control rod: any of a number of steel tubes, containing boron or another neutron absorber, that is inserted into the core of a nuclear reactor in order to control its rate of reaction
• nuclear reactor: any device in which a controlled chain reaction is maintained for the purpose of creating heat (for power generation) or for creating neutrons and other fission products for experimental, medical, or other purposes
• fission: The process of splitting the nucleus of an atom into smaller particles; nuclear fission.

Example

Some serious nuclear and radiation accidents have occurred. In 2011, three of the reactors at Fukushima I overheated, causing meltdowns that eventually led to explosions, which released large amounts of radioactive material into the air.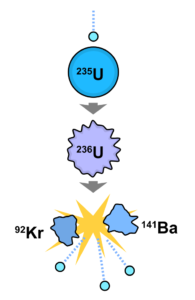

Nuclear fission is a nuclear reaction in which the nucleus of an atom splits into smaller (lighter) nuclei. This reaction often produces free neutrons and photons (in the form of gamma rays) and releases a very large amount of energy, even by the standards of radioactive decay . The two nuclei produced are most often of comparable but slightly different sizes, typically with a mass ratio of products of about 3 to 2, for common fissile nuclides.

Nuclear Fission Reaction:  An induced nuclear fission event. A neutron is absorbed by the nucleus of a uranium-235 atom, which in turn splits into fast-moving lighter elements (fission products) and free neutrons

For example, when a large fissile atomic nucleus such as uranium-235 or plutonium-239 absorbs a neutron, it may undergo nuclear fission. The heavy nucleus splits into two or more lighter nuclei (the fission products), releasing kinetic energy, gamma radiation, and free neutrons. A portion of these neutrons may later be absorbed by other fissile atoms and trigger further fission events, which release more neutrons, and so on. This is known as a nuclear chain reaction.
Just as conventional power stations generate electricity by harnessing the thermal energy released from burning fossil fuels, the thermal energy released from nuclear fission can be converted in electricity by nuclear reactors. A nuclear chain reaction can be controlled by using neutron poisons and neutron moderators to change the percentage of neutrons that will go on to cause more fissions. Nuclear reactors generally have automatic and manual systems to shut the fission reaction down if unsafe conditions are detected.
The reactor core generates heat in a number of ways. The kinetic energy of fission products is converted to thermal energy when these nuclei collide with nearby atoms. Some of the gamma rays produced during fission are absorbed by the reactor, and their energy is converted to heat. Heat is produced by the radioactive decay of fission products and materials that have been activated by neutron absorption. This decay heat source will remain for some time even after the reactor is shut down.
A nuclear reactor coolant — usually water, but sometimes a gas, liquid metal, or molten salt — is circulated past the reactor core to absorb the heat that it generates. The heat is carried away from the reactor and is then used to generate steam.
The power output of the reactor is adjusted by controlling how many neutrons are able to create more fissions. Control rods that are made of a neutron poison are used to absorb neutrons. Absorbing more neutrons in a control rod means that there are fewer neutrons available to cause fission, so pushing the control rod deeper into the reactor will reduce the reactor’s power output, and extracting the control rod will increase it.

Control Rod Assembly: Control rod assembly, above fuel element

Some serious nuclear and radiation accidents have occurred. Nuclear power plant accidents include the Chernobyl disaster (1986), the Fukushima Daiichi nuclear disaster (2011), the Three Mile Island accident (1979), and the SL-1 accident (1961).
Nuclear safety involves the actions taken to prevent nuclear and radiation accidents or to limit their consequences. The nuclear power industry has improved the safety and performance of reactors and has proposed new safer (but generally untested) reactor designs. However, there is no guarantee that these reactors will be designed, built, and operated correctly.

Fukushima Daiichi Nuclear Disaster: Satellite image taken March 16, 2011 of the four damaged reactor buildings

Emission Topography

Positron emission tomography is a nuclear medical imaging technique that produces a three-dimensional image of processes in the body.

Learning Objectives

Discuss possibility of uses of positron emission tomography with other diagnostic techniques.

Key Takeaways

KEY POINTS

• PET scanning utilizes detection of gamma rays emitted indirectly by a positron-emitting radionuclide (tracer), which is introduced into the body on a biologically active molecule.
• PET scans are increasingly read alongside CT or magnetic resonance imaging (MRI) scans, with the combination giving both anatomic and metabolic information.
• PET scanning is non-invasive, but it does involve exposure to ionizing radiation.

KEY TERMS

• tracer: A chemical used to track the progress or history of a natural process.
• positron: The antimatter equivalent of an electron, having the same mass but a positive charge.
• tomography: Imaging by sections or sectioning.

Positron emission tomography (PET) is a nuclear medical imaging technique that produces a three-dimensional image or picture of functional processes in the body. The system detects pairs of gamma rays emitted indirectly by a positron-emitting radionuclide (tracer), which is introduced into the body on a biologically active molecule. Three-dimensional images of tracer concentration within the body are then constructed by computer analysis.
PET acquisition process occurs as the radioisotope undergoes positron emission decay (also known as positive beta decay), it emits a positron, an antiparticle of the electron with opposite charge. The emitted positron travels in tissue for a short distance (typically less than 1 mm, but dependent on the isotope), during which time it loses kinetic energy, until it decelerates to a point where it can interact with an electron. The encounter annihilates both electron and positron, producing a pair of annihilation (gamma) photons moving in approximately opposite directions. These are detected when they reach a scintillator in the scanning device, creating a burst of light which is detected by photomultiplier tubes or silicon avalanche photodiodes . The technique depends on simultaneous or coincident detection of the pair of photons moving in approximately opposite directions (it would be exactly opposite in their center of mass frame, but the scanner has no way to know this, and so has a built-in slight direction-error tolerance). Photons that do not arrive in temporal “pairs” (i.e. within a timing-window of a few nanoseconds) are ignored.

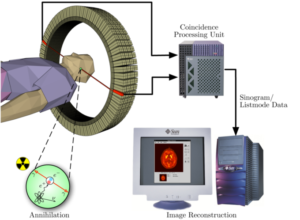
Positron Emission Tomography Acquisition Process: Schema of a PET acquisition process.

A technique much like the reconstruction of computed tomography (CT) and single-photon emission computed tomography (SPECT) data is more commonly used, although the data set collected in PET is much poorer than CT, so reconstruction techniques are more difficult.
PET scans are increasingly read alongside CT or magnetic resonance imaging (MRI) scans, with the combination giving both anatomic and metabolic information. Because PET imaging is most useful in combination with anatomical imaging, such as CT, modern PET scanners are now available with integrated high-end multi-detector-row CT scanners . Because the two scans can be performed in immediate sequence during the same session, with the patient not changing position between the two types of scans, the two sets of images are more-precisely registered, so that areas of abnormality on the PET imaging can be more perfectly correlated with anatomy on the CT images. This is very useful in showing detailed views of moving organs or structures with higher anatomical variation, which is more common outside the brain.

PET/CT-System:  PET/CT-System with 16-slice CT; the ceiling mounted device is an injection pump for CT contrast agent.

PET scanning is non-invasive, but it does involve exposure to ionizing radiation. The total dose of radiation is significant, usually around 5–7 mSv. However, in modern practice, a combined PET/CT scan is almost always performed, and for PET/CT scanning, the radiation exposure may be substantial—around 23–26 mSv (for a 70 kg person—dose is likely to be higher for higher body weights). When compared to the classification level for radiation workers in the UK of 6 mSv, it can be seen that use of a PET scan needs proper justification.

Nuclear Weapons

A nuclear weapon is an explosive device that derives its destructive force from nuclear reactions—either fission, fusion, or a combination.

Learning Objectives

Explain the difference between an “atomic” bomb and a “hydrogen” bomb, discussing their history

Key Takeaways

KEY POINTS

• Nuclear weapons utilize either fission (“atomic” bomb) or combination of fission and fusion (“hydrogen” bomb).
• Nuclear weapons are considered weapons of mass destruction.
• The use and control of nuclear weapons is a major focus of international relations policy since their first use.

KEY TERMS

• warfare: The waging of war or armed conflict against an enemy.
• fission: The process of splitting the nucleus of an atom into smaller particles; nuclear fission.
• fusion: A nuclear reaction in which nuclei combine to form more massive nuclei with the concomitant release of energy.

A nuclear weapon is an explosive device that derives its destructive force from nuclear reactions, either fission or a combination of fission and fusion. Both reactions release vast quantities of energy from relatively small amounts of matter. The first fission (i.e., “atomic”) bomb test released the same amount of energy as approximately 20,000 tons of trinitrotoluene (TNT). The first fusion (i.e., thermonuclear “hydrogen”) bomb test released the same amount of energy as approximately 10,000,000 tons of TNT.
A modern thermonuclear weapon weighing little more than 2,400 pounds (1,100 kg) can produce an explosive force comparable to the detonation of more than 1.2 million tons (1.1 million tonnes) of TNT. Thus, even a small nuclear device no larger than traditional bombs can devastate an entire city by blast, fire and radiation. Nuclear weapons are considered weapons of mass destruction, and their use and control have been a major focus of international relations policy since their inception.
Only two nuclear weapons have been used in the course of warfare, both by the United States near the end of World War II. On August 6, 1945, a uranium gun-type fission bomb code-named “Little Boy” was detonated over the Japanese city of Hiroshima. Only three days later a plutonium implosion-type fission bomb code-named “Fat Man” (as illustrated in ) was exploded over Nagasaki, Japan. The resulting mushroom cloud is shown in . The death toll from the two bombings was estimated at approximately 200,000 people—mostly civilians, and mainly from acute injuries sustained from the explosions. The role of the bombings in Japan’s surrender, and their ethical implications, remain the subject of scholarly and popular debate.

Nagasaki Atomic Bombing: The mushroom cloud of the atomic bombing of Nagasaki, Japan (August 9,1945) rose some 18 kilometers (11 mi) above the bomb’s hypocenter.

Fat Man Atomic Bomb:  The first nuclear weapons were gravity bombs, such as this “Fat Man” weapon dropped on Nagasaki, Japan. They were very large and could only be delivered by heavy bomber aircraft.

Since the bombings of Hiroshima and Nagasaki, nuclear weapons have been detonated on over two thousand occasions for testing purposes and demonstrations. Only a small number of nations either possess such weapons, or are suspected of trying to acquire and/or develop them. The only countries known to have detonated nuclear weapons (and that acknowledge possessing such weapons) are, as listed chronologically by date of first test: the United States, the Soviet Union (succeeded as a nuclear power by Russia), the United Kingdom, France, the People’s Republic of China, India, Pakistan, and North Korea. In addition, it is also widely believed that Israel possesses nuclear weapons (though they have not admitted to it).
The Federation of American Scientists estimates that as of 2012, there are more than 17,000 nuclear warheads in the world, with around 4,300 considered “operational”—as in ready for use.

NMR and MRIs

Magnetic resonance imaging is a medical imaging technique used in radiology to visualize internal structures of the body in detail.

Learning Objectives

Explain the difference between magnetic resonance imaging and computed tomography.

Key Takeaways

KEY POINTS

• MRI makes use of the property of nuclear magnetic resonance to image nuclei of atoms inside the body.
• MRI provides good contrast between the different soft tissues of the body (making it especially useful in imaging the brain, the muscles, the heart, and cancerous tissue).
• Although MRI uses non-ionizing radiation, the strong magnetic fields and radio pulses can affect metal implants, including cochlear implants and cardiac pacemakers.

KEY TERMS

• computed tomography: (CT) – A form of radiography which uses computer software to create images, or slices, at various planes of depth from images taken around a body or volume of interest.
• nuclear magnetic resonance: (NMRI) – The absorption of electromagnetic radiation (radio waves), at a specific frequency, by an atomic nucleus placed in a strong magnetic field; used in spectroscopy and in magnetic resonance imaging.
• magnetic resonance imaging: Commonly referred to as MRI; a technique that uses nuclear magnetic resonance to form cross sectional images of the human body for diagnostic purposes.

Magnetic resonance imaging (MRI), also called nuclear magnetic resonance imaging (NMRI) or magnetic resonance tomography (MRT), is a medical imaging technique used in radiology to visualize internal structures of the body in detail. MRI utilized the property of nuclear magnetic resonance (NMR) to image the nuclei of atoms inside the body.
MRI machines (as pictured in ) make use of the fact that body tissue contains a large amount of water and therefore protons (1H nuclei), which get aligned in a large magnetic field. Each water molecule has two hydrogen nuclei or protons. When a person is inside the scanner’s powerful magnetic field, the hydrogen protons in their body align with the direction of the field. A radio frequency current is briefly activated, producing a varying electromagnetic field. This electromagnetic field has just the right frequency (known as the resonance frequency) to become absorbed and then reverse the rotation of the hydrogen protons in the magnetic field.

MRI Scanner: Phillips MRI scanner in Gothenburg, Sweden.

After the electromagnetic field is turned off, the rotations of the hydrogen protons return to thermodynamic equilibrium, and then realign with the static magnetic field. During this relaxation, a radio frequency signal (electromagnetic radiation in the RF range) is generated; this signal can be measured with receiver coils. Hydrogen protons in different tissues return to their equilibrium state at different relaxation rates. Images are then constructed by performing a complex mathematical analysis of the signals emitted by the hydrogen protons.
MRI shows a marked contrast between the different soft tissues of the body, making it especially useful in imaging the brain, the muscles, the heart, and cancerous tissue—as compared with other medical imaging techniques such as computed tomography (CT) or X-rays. MRI contrast agents may be injected intravenously to enhance the appearance of blood vessels, tumors or inflammation.
Unlike CT, MRI does not use ionizing radiation and is generally a very safe procedure. The strong magnetic fields and radio pulses can, however, affect metal implants (including cochlear implants and cardiac pacemakers).

 

 

 

                                    XXX  .  V000000  Electron microscopes  

 

 

                                         

 

hat's the smallest thing you've ever seen? Maybe a hair, a pinhead, or a spec of dust? If you swapped your eyes for a couple of the world's most powerful microscopes, you'd be able to see things 100 million times smaller: bacteria, viruses, molecules—even the atoms in crystals would be clearly visible to you!

Ordinary optical microscopes (light-based microscopes), like the ones you find in a school lab, are nowhere near good enough to see things in such detail. It takes a much more powerful electron microscope—using beams of electrons instead of rays of light—to take us down to nano-dimensions. Let's take a closer look at electron microscopes and how they work!

Photo: This electron microscope at Argonne National Laboratory can produce images 1000 times sharper than any conventional optical (light-based) microscope. By courtesy of US Department of Energy.

Seeing with electrons

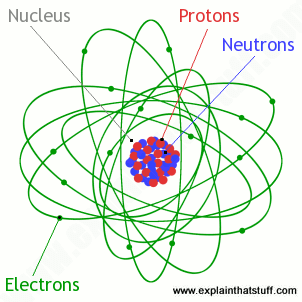
Photo: Inside an atom: electrons are the particles in shells (orbitals) around the nucleus (center).

We can see objects in the world around us because light rays (either from the Sun or from another light source, like a desktop lamp) reflect off them and into our eyes. No-one really knows what light is like, but scientists have settled on the idea that it has a sort of split personality. They like to call this wave-particle duality, but the basic idea is much simpler than it sounds. Sometimes light behaves like a train of waves—much like waves traveling over the sea. Other times, it's more like a steady stream of particles—a bombardment of microscopic cannonballs, if you like. You can read these words on your computer screen because light particles are streaming out of the display into your eyes in a kind of mass, horizontal hailstorm! We call these individual particles of light photons: each one is a tiny packet of electromagnetic energy.

Seeing with photons is fine if you want to look at things that are much bigger than atoms. But if you want to see things that are smaller, photons turn out to be pretty clumsy and useless. Just imagine if you were a master wood carver, renowned the world over for the finely carved furniture you made. To carve such fine details, you'd need small, sharp, precise tools smaller than the patterns you wanted to make. If all you had were a sledgehammer and a spade, carving intricate furniture would be impossible. The basic rule is that the tools you use have to be smaller than the things you're using them on.

And the same goes for science. The smallest thing you can see with a microscope is determined (partly) by the light that shines through it. An ordinary light microscope uses photons of light, which are equivalent to waves with a wavelength of roughly 400–700 nanometers. That's fine for studying something like a human hair, which is about 100 times bigger (50,000–100,000 nanometers in diameter). But what about a bacteria that's 200 nanometers across or a protein just 10 nanometers long? If you want to see finely detailed things that are "smaller than light" (smaller than the wavelength of photons), you need to use particles that have an even shorter wavelength than photons: in other words, you need to use electrons. As you probably know, electrons are the minute charged particles that occupy the outer regions of atoms. (They're also the particles that carry electricity around circuits.) In an electron microscope, a stream of electrons takes the place of a beam of light. An electron has an equivalent wavelength of just over 1 nanometer, which allows us to see things smaller even than light itself (smaller than the wavelength of light's photons).

How electron microscopes work

If you've ever used an ordinary microscope, you'll know the basic idea is simple. There's a light at the bottom that shines upward through a thin slice of the specimen. You look through an eyepiece and a powerful lens to see a considerably magnified image of the specimen (typically 10–200 times bigger). So there are essentially four important parts to an ordinary microscope:

1. The source of light.
2. The specimen.
3. The lenses that makes the specimen seem bigger.
4. The magnified image of the specimen that you see.

In an electron microscope, these four things are slightly different.

1. The light source is replaced by a beam of very fast moving electrons.
2. The specimen usually has to be specially prepared and held inside a vacuum chamber from which the air has been pumped out (because electrons do not travel very far in air).
3. The lenses are replaced by a series of coil-shaped electromagnets through which the electron beam travels. In an ordinary microscope, the glass lenses bend (or refract) the light beams passing through them to produce magnification. In an electron microscope, the coils bend the electron beams the same way.
4. The image is formed as a photograph (called an electron micrograph) or as an image on a TV screen.

That's the basic, general idea of an electron microscope. But there are actually quite a few different types of electron microscopes and they all work in different ways. The three most familiar types are called transmission electron microscopes (TEMs), scanning electron microscopes (SEMs), and scanning tunneling microscopes (STMs).

Photo: Left: Studying a specimen with a transmission electron microscope. The electron gun is in the tall gray tube at the top. By courtesy of NASA Glenn Research Center. Right A typical scanning electron microscope. The main microscope equipment is on the extreme left. You can see the image it produces on the two screens. By courtesy of NASA Langley Research Center.

Transmission electron microscopes (TEMs)

A TEM has a lot in common with an ordinary optical microscope. You have to prepare a thin slice of the specimen quite carefully (it's a fairly laborious process) and sit it in a vacuum chamber in the middle of the machine. When you've done that, you fire an electron beam down through the specimen from a giant electron gun at the top. The gun uses electromagnetic coils and high voltages (typically from 50,000 to several million volts) to accelerate the electrons to very high speeds. Thanks to our old friend wave-particle duality, electrons (which we normally think of as particles) can behave like waves (just as waves of light can behave like particles). The faster they travel, the smaller the waves they form and the more detailed the images they show up. Having reached top speed, the electrons zoom through the specimen and out the other side, where more coils focus them to form an image on screen (for immediate viewing) or on a photographic plate (for making a permanent record of the image). TEMs are the most powerful electron microscopes: we can use them to see things just 1 nanometer in size, so they effectively magnify by a million times or more.

How a transmission electron microscope (TEM) works

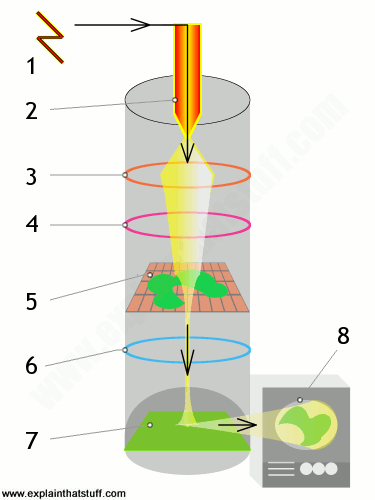
A transmission electron microscope fires a beam of electrons through a specimen to produce a magnified image of an object.

1. A high-voltage electricity supply powers the cathode.
2. The cathode is a heated filament, a bit like the electron gun in an old-fashioned cathode-ray tube (CRT) TV. It generates a beam of electrons that works in an analogous way to the beam of light in an optical microscope.
3. An electromagnetic coil (the first lens) concentrates the electrons into a more powerful beam.
4. Another electromagnetic coil (the second lens) focuses the beam onto a certain part of the specimen.
5. The specimen sits on a copper grid in the middle of the main microscope tube. The beam passes through the specimen and "picks up" an image of it.
6. The projector lens (the third lens) magnifies the image.
7. The image becomes visible when the electron beam hits a fluorescent screen at the base of the machine. This is analogous to the phosphor screen at the front of an old-fashioned TV .
8. The image can be viewed directly (through a viewing portal), through binoculars at the side, or on a TV monitor attached to an image intensifier (which makes weak images easier to see).

Scanning electron microscopes (SEMs)

Most of the funky electron microscope images you see in books—things like wasps holding microchips in their mouths—are not made by TEMs but by scanning electron microscopes (SEMs), which are designed to make images of the surfaces of tiny objects. Just as in a TEM, the top of a SEM is a powerful electron gun that shoots an electron beam down at the specimen. A series of electromagnetic coils pull the beam back and forth, scanning it slowly and systematically across the specimen's surface. Instead of traveling through the specimen, the electron beam effectively bounces straight off it. The electrons that are reflected off the specimen (known as secondary electrons) are directed at a screen, similar to a cathode-ray TV screen, where they create a TV-like picture. SEMs are generally about 10 times less powerful than TEMs (so we can use them to see things about 10 nanometers in size). On the plus side, they produce very sharp, 3D images (compared to the flat images produced by TEMs) and their specimens need less preparation.

Photo: Typical images produced by a SEM. Left: An artificially colored, scanning electron micrograph showing Salmonella typhimurium (red) invading cultured human cells. Right: A scanning electron micrograph of the bacteria Escherichia coli (E.coli). Photos by courtesy of Rocky Mountain Laboratories, US National Institute of Allergy and Infectious Diseases (NIAID), and US National Institute of Health.

How a scanning electron microscope (SEM) works

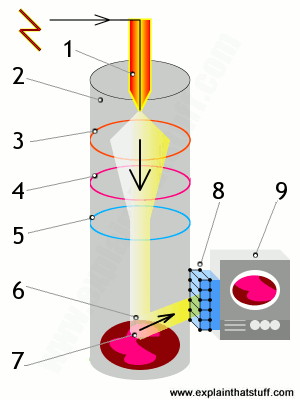
A scanning electron microscope scans a beam of electrons over a specimen to produce a magnified image of an object. That's completely different from a TEM, where the beam of electrons goes right through the specimen.

1. Electrons are fired into the machine.
2. The main part of the machine (where the object is scanned) is contained within a sealed vacuum chamber because precise electron beams can't travel effectively through air.
3. A positively charged electrode (anode) attracts the electrons and accelerates them into an energetic beam.
4. An electromagnetic coil brings the electron beam to a very precise focus, much like a lens.
5. Another coil, lower down, steers the electron beam from side to side.
6. The beam systematically scans across the object being viewed.
7. Electrons from the beam hit the surface of the object and bounce off it.
8. A detector registers these scattered electrons and turns them into a picture.
9. A hugely magnified image of the object is displayed on a TV screen.

Scanning tunneling microscopes (STMs)

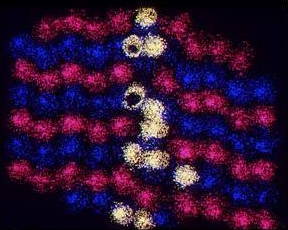
Photo: An STM image of the atoms on the surface of a solar cell. By courtesy of US Department of Energy/National Renewable Energy Laboratory (NREL).
Among the newest electron microscopes, STMs were invented by Gerd Binnig and Heinrich Rohrer in 1981. Unlike TEMs, which produce images of the insides of materials, and SEMs, which show up 3D surfaces, STMs are designed to make detailed images of the atoms or molecules on the surface of something like a crystal. They work differently to TEMs and SEMs too: they have an extremely sharp metallic probe that scans back and forth across the surface of the specimen. As it does so, electrons try to wriggle out of the specimen and jump across the gap, into the probe, by an unusual phenomenon called "tunneling". The closer the probe is to the surface, the easier it is for electrons to tunnel into it, the more electrons escape, and the greater the tunneling current. The microscope constantly moves the probe up or down by tiny amounts to keep the tunneling current constant. By recording how much the probe has to move, it effectively measures the peaks and troughs of the specimen's surface. A computer turns this information into a map of the specimen that shows up its detailed atomic structure. One big drawback of ordinary electron microscopes is that they produce amazing detail using high-energy beams of electrons, which tend to damage the objects they're imaging. STMs avoid this problem by using much lower energies.

Atomic force microscopes (AFMs)

If you think STMs are amazing, AFMs (atomic force microscopes), also invented by Gerd Binnig, are even better! One of the big drawbacks of STMs is that they rely on electrical currents (flows of electrons) passing through materials, so they can only make images of conductors. AFMs don't suffer from this problem because, although they use still tuneling, they don't rely on a current flowing between the specimen and a proble, so we can use them to make atomic-scale images of materials such as plastics, which don't conduct electricity.
An AFM is a microscope with a little arm called a cantilever with a tip on the end that scans across the surface of a specimen. As the tip sweeps across the surface, the force between the atoms from which it's made and the atoms on the surface constantly changes, causing the cantilever to bend by minute amounts. The amount by which the cantilever bends is detected by bouncing a laser beam off its surface. By measuring how far the laser beam travels, we can measure how much the cantilever bends and the forces acting on it from moment to moment, and that information can be used to figure out and plot the contours of the surface. Other versions of AFMs (like the one illustrated here) make an image by measuring a current that "tunnels" between the scanning tip and a tunneling probe mounted just behind it. AFMs can make images of things at the atomic level and they can also be used to manipulate individual atoms and molecules—one of the key ideas in nanotechnology.

Artwork: How Gerd Binnig's original AFM worked—greatly simplified. The specimen to be scanned (1) is mounted on a drive mechanism (2) that can move it in three dimensions. To prevent unwanted vibrations, that mechanism is fixed to a rubber cushion (3) mounted on a firm aluminum base (4), which is further cushioned by multiple layers of aluminum plates and rubber pads (not shown). To create an image, the specimen is slowly moved around the sharp, fixed imaging point (5), which is mounted on a spring cantilever made of thin gold foil (6), attached to a piezoelectric crystal (7), and fixed to the same aluminum base. At the other end of the apparatus, a tunneling probe (8) is moved very close (to within about 0.3nm) of the spring cantilever by a second drive mechanism (9), isolated by another rubber cushion (10). As the sample (1) moves around the imaging point (5), the current that tunnels between the spring cantilever (6) and the tunneling tip (8) is constantly measured. These measurements are converted into data that can be used to draw a detailed surface map of the specimen. Based on an original drawing from Gerd Binnig's US Patent 4,724,318: Atomic force microscope and method for imaging surfaces with atomic resolution.

Who invented electron microscopes?

Here's a brief history of the key moments in electron microscopy—so far!

• 1924: French physicist Louis de Broglie (1892–1987) realizes that electron beams have a wavelike nature similar to light. Five years later, he wins the Nobel Prize in Physics for this work.
• 1931: German scientists Max Knoll (1897–1969) and his pupil Ernst Ruska (1906–1988) build the first experimental TEM in Berlin.
• 1933: Ernst Ruska builds the first electron microscope that is more powerful than an optical microscope.
• 1935: Max Knoll builds the first crude SEM.
• 1941: German electrical engineers Manfred Von Ardenne and Bodo von Borries patent an "electron scanning microscope" (SEM).
• 1965: Cambridge Instrument Company produces the first commercial SEM in England.
• 1981: Gerd Binnig (1947–) and Heinrich Rohrer (1933–) of IBM's Zurich Research Laboratory invent the STM and produce detailed images of atoms on the surface of a crystal of gold.
• 1985: Binnig and his colleague Christoph Gerber produce the first atomic force microscope (AFM) by attaching a diamond to a piece of gold foil.
• 1986: Binnig and Rohrer share the Nobel Prize in Physics with the original pioneer of electron microscopes, Ernst Ruska.
• 1989: The first commercial AFM is produced by Sang-il Park (founder of Park Systems of Palo Alto, California

     

         Tools, instruments, and measurement

Tools and equipment

• Autoclaves: How can you kill germs with high-pressure steam?
• Binoculars: How do they work? What's the best kind to buy?
• Chainsaws: How much faster can you cut down a tree if you have a gasoline engine to help you?
• Defibrillators: How can you use electricity to restart someone's heart?
• Fire fighting: What's inside a fire engine? What do fire hydrants do?
• Fire extinguishers: How does a fire extinguisher work?
• Fire sprinklers: How does a fire sprinkler know when a fire's broken out?
• Jackhammers/pneumatic drills: How can high-pressure air smash holes in the pavement?
• Pressure washers: What's so good about a squirt of hot water?
• Pulleys: How can ropes and wheels help you lift four, five, or ten times as much?
• Robots: Will robots ever take over from people?
• Tools and machines: What exactly is a machine and why is it so useful?
• Welding and soldering: What's the difference between them?

Instruments and measuring devices

• Accelerometers: Measure force or acceleration in everything from crash-test dummies to cellphones.
• Altimeters: Measure altitude in a plane to ensure you'll flying safely.
• Anemometers: Measure wind speed (and stop wind turbines spinning out of control).
• Barometers: Measure pressure and help us forecast the weather.
• Blood-pressure monitors: Check your blood pressure and indicate problems with your health.
• Carbon monoxide detectors: Spot leaks of toxic gas from fuel-burning appliances.
• Chromatography: Use color-changes to analyze chemicals in a sample.
• Compasses: Show you the way home by aligning with Earth's magnetic field.
• Dynamometers: Measure the driving power of an engine or machine.
• Geiger counters: Detect radiation with a burst of clicks.
• Hall-effect sensors: Measure a magnetic field with a tiny electronic chip.
• Hygrometers: Measure humidity in the air.
• Interferometers: Measure tiny distances by aligning laser beams.
• Iris scanners: Check your identity by looking into your eye.
• Mass spectrometers: Bend the particles in a sample into a kind of atomic rainbow.
• Metal detectors: Find buried treasure or check suspicious people for weapons.
• Pedometers: Count the steps you walk with a swinging pendulum.
• Pendulum clocks: Use a pendulum to tell time.
• pH meters: Measure the acidity of a liquid.
• Polygraphs ("lie detectors"): Give an idea of whether you're telling the truth.
• Pyranometers: Measure the amount of sunlight that's hitting Earth.
• Pyrometers: Measure temperature from the radiation given off by hot things.
• Quartz clocks and watches: Use a vibrating crystal to count time.
• Radio-controlled clocks (RCCs): Keep time using a radio link to an atomic clock.
• Schlieren photography: Photograph shock waves in the air caused by fast-moving objects.
• Sound level (decibel) meters: Measure how loud something sounds.
• Speedometers: Track how fast you're going.
• Strain gauges: Measure the force on a building or a static structure.
• Thermometers: Measure temperature, often using expanding liquids or solids.
• Thermostats: Keep a room at a constant temperature.
• Thermocouples: Measure the temperature of really hot things (such as volcanos).
• Weights and balances: Measure weight (the force of gravity) on objects around us.
• X rays: See inside your body with ghostly radio waves!

       

Tools, instruments, and measurement

Tools and equipment

• Autoclaves: How can you kill germs with high-pressure steam?
• Binoculars: How do they work? What's the best kind to buy?
• Chainsaws: How much faster can you cut down a tree if you have a gasoline engine to help you?
• Defibrillators: How can you use electricity to restart someone's heart?
• Fire fighting: What's inside a fire engine? What do fire hydrants do?
• Fire extinguishers: How does a fire extinguisher work?
• Fire sprinklers: How does a fire sprinkler know when a fire's broken out?
• Jackhammers/pneumatic drills: How can high-pressure air smash holes in the pavement?
• Pressure washers: What's so good about a squirt of hot water?
• Pulleys: How can ropes and wheels help you lift four, five, or ten times as much?
• Robots: Will robots ever take over from people?
• Tools and machines: What exactly is a machine and why is it so useful?
• Welding and soldering: What's the difference between them?

Instruments and measuring devices

• Accelerometers: Measure force or acceleration in everything from crash-test dummies to cellphones.
• Altimeters: Measure altitude in a plane to ensure you'll flying safely.
• Anemometers: Measure wind speed (and stop wind turbines spinning out of control).
• Barometers: Measure pressure and help us forecast the weather.
• Blood-pressure monitors: Check your blood pressure and indicate problems with your health.
• Carbon monoxide detectors: Spot leaks of toxic gas from fuel-burning appliances.
• Chromatography: Use color-changes to analyze chemicals in a sample.
• Compasses: Show you the way home by aligning with Earth's magnetic field.
• Dynamometers: Measure the driving power of an engine or machine.
• Geiger counters: Detect radiation with a burst of clicks.
• Hall-effect sensors: Measure a magnetic field with a tiny electronic chip.
• Hygrometers: Measure humidity in the air.
• Interferometers: Measure tiny distances by aligning laser beams.
• Iris scanners: Check your identity by looking into your eye.
• Mass spectrometers: Bend the particles in a sample into a kind of atomic rainbow.
• Metal detectors: Find buried treasure or check suspicious people for weapons.
• Pedometers: Count the steps you walk with a swinging pendulum.
• Pendulum clocks: Use a pendulum to tell time.
• pH meters: Measure the acidity of a liquid.
• Polygraphs ("lie detectors"): Give an idea of whether you're telling the truth.
• Pyranometers: Measure the amount of sunlight that's hitting Earth.
• Pyrometers: Measure temperature from the radiation given off by hot things.
• Quartz clocks and watches: Use a vibrating crystal to count time.
• Radio-controlled clocks (RCCs): Keep time using a radio link to an atomic clock.
• Schlieren photography: Photograph shock waves in the air caused by fast-moving objects.
• Sound level (decibel) meters: Measure how loud something sounds.
• Speedometers: Track how fast you're going.
• Strain gauges: Measure the force on a building or a static structure.
• Thermometers: Measure temperature, often using expanding liquids or solids.
• Thermostats: Keep a room at a constant temperature.
• Thermocouples: Measure the temperature of really hot things (such as volcanos).
• Weights and balances: Measure weight (the force of gravity) on objects around us.
• X rays: See inside your body with ghostly radio waves!

        

                                                          



                                                                      Telescope   


A telescope is an optical instrument that aids in the observation of remote objects by collecting electromagnetic radiation (such as visible light). The first known practical telescopes were invented in the Netherlands at the beginning of the 17th century, by using glass lenses. They found use in both terrestrial applications and astronomy.
Within a few decades, the reflecting telescope was invented, which used mirrors to collect and focus the light. In the 20th century, many new types of telescopes were invented, including radio telescopes in the 1930s and infrared telescopes in the 1960s. The word telescope now refers to a wide range of instruments capable of detecting different regions of the electromagnetic spectrum, and in some cases other types of detectors.
The word telescope (from the Ancient Greek τῆλε, tele "far" and σκοπεῖν, skopein "to look or see"; τηλεσκόπος, teleskopos "far-seeing") was coined in 1611 by the Greek mathematician Giovanni Demisiani for one of Galileo Galilei's instruments presented at a banquet at the Accademia dei Lincei.^[1][2][3] In the Starry Messenger, Galileo had used the term perspicillum.


   

The 100 inch (2.54 m) Hooker reflecting telescope at Mount Wilson Observatory near Los Angeles, USA

History of the telescope

The "onion" dome at the Royal Observatory, Greenwich housing a 28-inch refracting telescope with a remaining segment of William Herschel's 120-centimetre (47 in) diameter reflecting telescope (called the "40-foot telescope" due to its focal length) in the foreground.

The earliest existing record of a telescope was a 1608 patent submitted to the government in the Netherlands by Middelburg spectacle maker Hans Lippershey for a refracting telescope.^[4] The actual inventor is unknown but word of it spread through Europe. Galileo heard about it and, in 1609, built his own version, and made his telescopic observations of celestial objects.^[5][6]
The idea that the objective, or light-gathering element, could be a mirror instead of a lens was being investigated soon after the invention of the refracting telescope.^[7] The potential advantages of using parabolic mirrors—reduction of spherical aberration and no chromatic aberration—led to many proposed designs and several attempts to build reflecting telescopes.^[8] In 1668, Isaac Newton built the first practical reflecting telescope, of a design which now bears his name, the Newtonian reflector.
The invention of the achromatic lens in 1733 partially corrected color aberrations present in the simple lens and enabled the construction of shorter, more functional refracting telescopes. Reflecting telescopes, though not limited by the color problems seen in refractors, were hampered by the use of fast tarnishing speculum metal mirrors employed during the 18th and early 19th century—a problem alleviated by the introduction of silver coated glass mirrors in 1857,^[9] and aluminized mirrors in 1932.^[10] The maximum physical size limit for refracting telescopes is about 1 meter (40 inches), dictating that the vast majority of large optical researching telescopes built since the turn of the 20th century have been reflectors. The largest reflecting telescopes currently have objectives larger than 10 m (33 feet), and work is underway on several 30-40m designs.
The 20th century also saw the development of telescopes that worked in a wide range of wavelengths from radio to gamma-rays. The first purpose built radio telescope went into operation in 1937. Since then, a large variety of complex astronomical instruments have been developed.

Types

The primary mirror assembly of James Webb Space Telescope under construction. This is a segmented mirror and its coated with Gold to reflect (orange-red) visible light, through near-infrared to the mid-infrared

The name "telescope" covers a wide range of instruments. Most detect electromagnetic radiation, but there are major differences in how astronomers must go about collecting light (electromagnetic radiation) in different frequency bands.
Telescopes may be classified by the wavelengths of light they detect:

• X-ray telescopes, using shorter wavelengths than ultraviolet light
• Ultraviolet telescopes, using shorter wavelengths than visible light
• Optical telescopes, using visible light
• Infrared telescopes, using longer wavelengths than visible light
• Submillimetre telescopes, using longer wavelengths than infrared light
• Fresnel Imager, an optical lens technology
• X-ray optics, optics for certain X-ray wavelengths

As wavelengths become longer, it becomes easier to use antenna technology to interact with electromagnetic radiation (although it is possible to make very tiny antenna). The near-infrared can be collected much like visible light, however in the far-infrared and submillimetre range, telescopes can operate more like a radio telescope. For example, the James Clerk Maxwell Telescope observes from wavelengths from 3 μm (0.003 mm) to 2000 μm (2 mm), but uses a parabolic aluminum antenna.^[11] On the other hand, the Spitzer Space Telescope, observing from about 3 μm (0.003 mm) to 180 μm (0.18 mm) uses a mirror (reflecting optics). Also using reflecting optics, the Hubble Space Telescope with Wide Field Camera 3 can observe in the frequency range from about 0.2 μm (0.0002 mm) to 1.7 μm (0.0017 mm) (from ultra-violet to infrared light).^[12]
With photons of the shorter wavelengths, with the higher frequencies, glancing-incident optics, rather than fully reflecting optics are used. Telescopes such as TRACE and SOHO use special mirrors to reflect Extreme ultraviolet, producing higher resolution and brighter images than are otherwise possible. A larger aperture does not just mean that more light is collected, it also enables a finer angular resolution.
Telescopes may also be classified by location: ground telescope, space telescope, or flying telescope. They may also be classified by whether they are operated by professional astronomers or amateur astronomers. A vehicle or permanent campus containing one or more telescopes or other instruments is called an observatory.

Modern telescopes typically use CCDs instead of film for recording images. This is the sensor array in the Kepler spacecraft.

Light Comparison
Name	Wavelength	Frequency (Hz)	Photon Energy (eV)
Gamma ray	less than 0.01 nm	more than 10 EHZ	100 keV – 300+ GeV	X
X-Ray	0.01 to 10 nm	30 EHz – 30 PHZ	120 eV to 120 keV	X
Ultraviolet	10 nm – 400 nm	30 PHZ – 790 THz	3 eV to 124 eV
Visible	390 nm – 750 nm	790 THz – 405 THz	1.7 eV – 3.3 eV	X
Infrared	750 nm – 1 mm	405 THz – 300 GHz	1.24 meV – 1.7 eV	X
Microwave	1 mm – 1 meter	300 GHz – 300 MHz	1.24 meV – 1.24 µeV
Radio	1 mm – km	300 GHz – 3 Hz	1.24 meV – 12.4 feV	X

Optical telescopes

50 cm refracting telescope at Nice Observatory.

Main article: Optical telescope

An optical telescope gathers and focuses light mainly from the visible part of the electromagnetic spectrum (although some work in the infrared and ultraviolet).^[13] Optical telescopes increase the apparent angular size of distant objects as well as their apparent brightness. In order for the image to be observed, photographed, studied, and sent to a computer, telescopes work by employing one or more curved optical elements, usually made from glass lenses and/or mirrors, to gather light and other electromagnetic radiation to bring that light or radiation to a focal point. Optical telescopes are used for astronomy and in many non-astronomical instruments, including: theodolites (including transits), spotting scopes, monoculars, binoculars, camera lenses, and spyglasses. There are three main optical types:

• The refracting telescope which uses lenses to form an image.
• The reflecting telescope which uses an arrangement of mirrors to form an image.
• The catadioptric telescope which uses mirrors combined with lenses to form an image.

Beyond these basic optical types there are many sub-types of varying optical design classified by the task they perform such as astrographs, comet seekers and solar telescopes.

Radio telescopes

The Very Large Array at Socorro, New Mexico, United States.

 

Radio telescopes are directional radio antennas used for radio astronomy. The dishes are sometimes constructed of a conductive wire mesh whose openings are smaller than the wavelength being observed. Multi-element Radio telescopes are constructed from pairs or larger groups of these dishes to synthesize large 'virtual' apertures that are similar in size to the separation between the telescopes; this process is known as aperture synthesis. As of 2005, the current record array size is many times the width of the Earth—utilizing space-based Very Long Baseline Interferometry (VLBI) telescopes such as the Japanese HALCA (Highly Advanced Laboratory for Communications and Astronomy) VSOP (VLBI Space Observatory Program) satellite. Aperture synthesis is now also being applied to optical telescopes using optical interferometers (arrays of optical telescopes) and aperture masking interferometry at single reflecting telescopes. Radio telescopes are also used to collect microwave radiation, which is used to collect radiation when any visible light is obstructed or faint, such as from quasars. Some radio telescopes are used by programs such as SETI and the Arecibo Observatory to search for extraterrestrial life.

X-ray telescopes

Einstein Observatory was a space-based focusing optical X-ray telescope from 1978.^[14]

Main article: X-ray telescope

X-ray telescopes can use X-ray optics, such as a Wolter telescopes composed of ring-shaped 'glancing' mirrors made of heavy metals that are able to reflect the rays just a few degrees. The mirrors are usually a section of a rotated parabola and a hyperbola, or ellipse. In 1952, Hans Wolter outlined 3 ways a telescope could be built using only this kind of mirror.^[15][16] Examples of an observatory using this type of telescope are the Einstein Observatory, ROSAT, and the Chandra X-Ray Observatory. By 2010, Wolter focusing X-ray telescopes are possible up to 79 keV.^[14]

Gamma-ray telescopes

Higher energy X-ray and Gamma-ray telescopes refrain from focusing completely and use coded aperture masks: the patterns of the shadow the mask creates can be reconstructed to form an image.
X-ray and Gamma-ray telescopes are usually on Earth-orbiting satellites or high-flying balloons since the Earth's atmosphere is opaque to this part of the electromagnetic spectrum. However, high energy X-rays and gamma-rays do not form an image in the same way as telescopes at visible wavelengths. An example of this type of telescope is the Fermi Gamma-ray Space Telescope.
The detection of very high energy gamma rays, with shorter wavelength and higher frequency than regular gamma rays, requires further specialization. An example of this type of observatory is VERITAS. Very high energy gamma-rays are still photons, like visible light, whereas cosmic rays includes particles like electrons, protons, and heavier nuclei.
A discovery in 2012 may allow focusing gamma-ray telescopes.^[17] At photon energies greater than 700 keV, the index of refraction starts to increase again.^[17]

High-energy particle telescopes

High-energy astronomy requires specialized telescopes to make observations since most of these particles go through most metals and glasses.
In other types of high energy particle telescopes there is no image-forming optical system. Cosmic-ray telescopes usually consist of an array of different detector types spread out over a large area. A Neutrino telescope consists of a large mass of water or ice, surrounded by an array of sensitive light detectors known as photomultiplier tubes. Originating direction of the neutrinos is determined by reconstructing the path of secondary particles scattered by neutrino impacts, from their interaction with multiple detectors. Energetic neutral atom observatories like Interstellar Boundary Explorer detect particles traveling at certain energies.

Other types of telescopes

Equatorial-mounted Keplerian telescope

Astronomy is not limited to using electromagnetic radiation. Additional information can be obtained using other media. The detectors used to observe the Universe are analogous to telescopes. These are:

• Gravitational-wave detector, the equivalent of a gravitational wave telescope, used for gravitational-wave astronomy.
• Neutrino detector, the equivalent of a neutrino telescope, used for neutrino astronomy.

Types of mount

A telescope mount is a mechanical structure which supports a telescope. Telescope mounts are designed to support the mass of the telescope and allow for accurate pointing of the instrument. Many sorts of mounts have been developed over the years, with the majority of effort being put into systems that can track the motion of the stars as the Earth rotates. The two main types of tracking mount are:

• Altazimuth mount
• Equatorial mount

Atmospheric electromagnetic opacity

Since the atmosphere is opaque for most of the electromagnetic spectrum, only a few bands can be observed from the Earth's surface. These bands are visible – near-infrared and a portion of the radio-wave part of the spectrum. For this reason there are no X-ray or far-infrared ground-based telescopes as these have to be observed from orbit. Even if a wavelength is observable from the ground, it might still be advantageous to place a telescope on a satellite due to astronomical seeing.

A diagram of the electromagnetic spectrum with the Earth's atmospheric transmittance (or opacity) and the types of telescopes used to image parts of the spectrum.

Telescopic image from different telescope types

Different types of telescope, operating in different wavelength bands, provide different information about the same object. Together they provide a more comprehensive understanding.

A 6′ wide view of the Crab nebula supernova remnant, viewed at different wavelengths of light by various telescopes

By spectrum

Telescopes that operate in the electromagnetic spectrum:

Name	Telescope	Astronomy	Wavelength
Radio	Radio telescope	Radio astronomy (Radar astronomy)	more than 1 mm
Submillimetre	Submillimetre telescopes*	Submillimetre astronomy	0.1 mm – 1 mm
Far Infrared	–	Far-infrared astronomy	30 µm – 450 µm
Infrared	Infrared telescope	Infrared astronomy	700 nm – 1 mm
Visible	Visible spectrum telescopes	Visible-light astronomy	400 nm – 700 nm
Ultraviolet	Ultraviolet telescopes*	Ultraviolet astronomy	10 nm – 400 nm
X-ray	X-ray telescope	X-ray astronomy	0.01 nm – 10 nm
Gamma-ray	–	Gamma-ray astronomy	less than 0.01 nm

=====  MA THEREFORE ELECTRONICS MICROSCOPE AND TELESCOPE MATIC =====