material, mass and usability CHEMISTRY

X . I Definition of matter, mass, and uses chemistry.
A. Materials
Matter is anything that has mass and occupies space. for example, water, stone, sand, soil, oxygen, wood, iron etc. while the substance is the designation designation for materials that are more specific (special). while the material is a term for materials that are less specific.
Mass
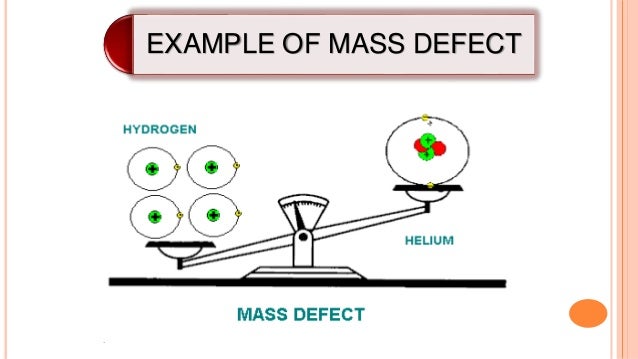
(Derived from the Greek μάζα) is a physical property of an object that is used to describe a variety of objects observed behavior. The mass of an object is the amount of substance (matter) contained in an object is. Mass of an object is different from the weight of an object. Mass of the object shows the amount of matter that make up the object. Therefore, the mass of its properties remain in all the places. Mass expressed in kilograms (KG). Of body weight is the force that states the amount of gravitational pull on objects that have mass. Therefore, the weight of an object will be different in different places. Because weight is a force, then the weight of the unit is the Newton (N). Two objects with the same mass when weighed in a place that has the same gravity, will have the same weight as well.
The usefulness of chemistry
can transform natural materials into a product (finished goods which can be used in everyday life,
humans can see and understand how to meet their needs,
humans a better understanding of the environment, and the process that occurs therein
people understand the symptoms that occur in everyday life,
people understand the processes occurring in the body and how to maintain good health.
Differences in physical properties and chemical properties
physical properties: properties of the material of his relationship with physical properties. while the physical change is the change in an object without forming a new substance
Chemical properties: chemical properties have a tendency to hold a chemical reaction, a change in chemistry is the change in an object that form new substances.
Physical and chemical changes
A physical change: the change in physics just happen to change shape without generating new compounds. examples of physical change is a change in the form, for example; the freezing process on ice, evaporation, sublimation, condensation and efflorescence. changes in the form, for example: of rice into flour, of wheat into flour, from the yarn into fabric change in taste by the senses, for example: changes in temperature, change in taste.
Chemical change, chemical change is the change of a substance or material that led to the formation material (new compounds), examples of chemical changes are: fuel combustion in motorcycles, from gasoline (liquid) into energy and exhaust fumes the process of photosynthesis in plants , which change the water, sunlight, minerals and carbon dioxide into food and oxygen
Distinguishing between elements and compounds, and mixtures homogeneous mixture of hydrogen
element
An element is a substance that can not be divided again into smaller parts.
Examples of elements:
- Elements Gold / Au ( Aurumn )
- Nitrogen / N
- Elements of Platina / Pt
- Elements of Carbon / Carbon /
Compound
The compound is a single substance consisting of several elements intertwined.
Examples Compounds:
- Compound Oxygen / O2
- Compound Water / H2O
- Compounds Alcohol / C2 H5 OH
- Compound Salt Kitchen / NaCl
Homogeneous mix
homo genous mixture is a mixture in which all parts of the mixture has a composition equal parts and a uniform, homogeneous mixture is often called a solution.
an example of a homogeneous solution is tea and milk, and milk including the solution of a homogeneous mixture because we could not distinguish the components of the solution and every component has a uniform composition in every part of the solution.
heterogeneous mix
heterogeneous mixture is a mixture of the arrangement is not uniform or not the same.
an example of a heterogeneous mixture is a mixture of gravel and soil, because we can still distinguish its components.
Explain the law of conservation of mass, comparative law and the law of multiple proportions Conservation of mass
conservation of mass put forward by by Antoine Laurent Lavoisier, which reads "in a reaction mass of matter before and after the reaction is the same" in other words the mass can not be created and destroyed, meaning that during the reaction no atoms reagents and atoms results reagents missing. Expressions commonly used to express the conservation of mass is the mass of deform able but can not be created or destroyed. For a chemical process in a closed system, the mass of the reactants must be equal to the mass of the product.
LAW OF CONSERVATION OF MASS = LAW Lavoisier"The mass of substances before and after the reaction is fixed".
Example:hydrogen + oxygen ® hydrogen oxide(4g) (32g) (36G)
Law of definite proportions
Law of definite proportions found by Joseph Proust, a French chemist. Law of definite proportions states, as the name suggests, "the mass ratio of the elements in a compound is limited and fixed". Thus, any compound anywhere and consist of a definite mass ratio.
Example:a. On the NH3 compound: mass N: mass H= 1 Ar. N: 3 Ar. H= 1 (14): 3 (1) = 14: 3b. On SO3 compound: mass S: mass 0= 1 Ar. S: 3 Ar. O= 1 (32): 3 (16) = 32: 48 = 2: 3
Advantages of law Proust:if known mass of a compound or a mass of one of the elements that make up the compound of make masses of other elements can be known.
Example:How many levels of C in 50 grams of CaCO3? (Ar: C = 12; 0 = 16; Ca = 40)Mass C = (Ar C / Mr CaCO3) x mass of CaCO3= 12/100 x 50 gram = 6 gramsmass CLevels of C = C mass / mass CaCO3 x 100%= 6/50 x 100% = 12%
Law of multiple proportions
At the time of filing of this law, the chemical formula of unknown compounds. This law proposed John Dalton, British chemist and inventor of modern atomic theory. This law states that "if the mass of one of the two elements in the same compound, the mass ratio of the other elements is an integer and simple".
Example:
When the elements of oxygen compounded den Nitrogen can be formed,NO where mass N: 0 = 14: 16 = 7: 8NO2 in which the mass of N: 0 = 14: 32 = 7: 16
Nitrogen for the masses as much the mass ratio of oxygen in the compound NO: NO2 = 8: 16 = 1: 2
X . II understanding and definition of mass and weight

Definition / Definitions Mass
Mass is a quantity that indicates the size of inertia (inertia or also known as inertia is the tendency of all physical objects to resist changes to the state of motion) owned by an object or the number of particles contained substances. Mass of an object will not be changed or fixed no matter where it is located.
Definition / Definitions Weight
Weight is a quantity that indicates the size of the acceleration of gravity affecting the mass of the object, the weight of an object can change depending on the acceleration of gravity in an environment where the existence of the object. For example, the weight of an object on the earth will be different with the weight of the object on the moon, because of the gravitational acceleration of the earth and moon are different. To search for an object simply multiply the weight of the object's mass and gravitational acceleration, the following formula:
Equation formula Gravity
w = m x g
Information:
w = weight of the object (N / Newton)
m = mass of the object (kg / Kilogram)
g = acceleration due to gravity (m / s2 or N / kg)
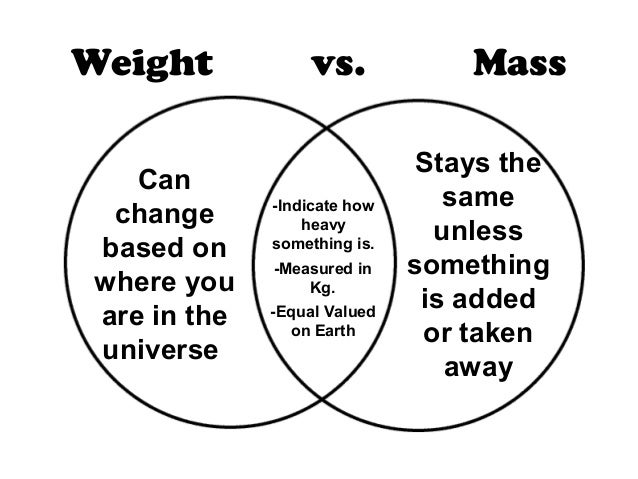
Differences Mass and Weight
Mass is the number of particles (amount of material) contained substances / objects, while the weight of the mass that is affected gravity.
Mass value has not changed / fixed, while the value of the weight may be changed, depending gravity where it is located.
Mass expressed in units kg (kilogram), while the weight is expressed in Newtons
Mass including scalar and principal, while the weight including vector and derivatives.
Mass is a quantity that does not have a direction, whereas the amount of weight that have a direction.
Mass was measured using the balance sheet, while the weight was measured using a spring balance or a dynamo meter.
conclusion: so ubiquitous in the same period is not affected by altitude, while the weight fluctuations are influenced by gravity height of objects .
material ExistenceWe recognize three kinds of matter, namely: solid, liquid, and gas. The characteristics of each of these materials, namely:
Solid: The shape and volume remain, as long as there is no influence from outside. For example, the shape and volume of a piece of iron remains, although placed in different places as long as there is no influence from outside.
Liquid: The form of a liquid changing the shape of the container. Placed in the glass, liquids take the shape of the bottle. But the volume of liquid is fixed.
Gas: The shape and volume are not fixed. Gas will fill the entire space available to him.
Mass and Weight MatterThe material has a mass and weight. Mass and weight are two different magnitudes. Each object has a mass, so that objects can be weighed to determine the amount of the materials on it. Something which occupies the space can be measured in volume. Mass of an object stating the amount of the materials on it. One of the properties of matter that is often used to distinguish and recognize a wide range of material is its density, which is mass divided by volume of material.
The density of each material specific to the material. Between the mass and volume of an object is no fixed relationship. The density of an object is not fixed, but depends on several factors, such as temperature and manifestations. In general, the mass of the object is reduced with temperature rise Understanding different mass to sense weight. Mass of an object remains in all places, while the weight of it depends on the place. Weight of an object is affected by the force of gravity.


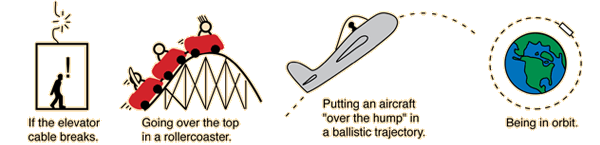
Weight Example
Many people get very, very, very confused on the subject of mass vs weight. The two are very different in ways that are very easily explained by just reading a few sentences.
These three things are what helps distinguish the big differences of mass and weight.
1) Mass is a measurement of the amount of matter something contains, while Weight is the measurement of the pull of gravity on an object.
2) Mass is measured by using a balance comparing a known amount of matter to an unknown amount of matter. Weight is measured on a scale.
3) The Mass of an object doesn't change when an object's location changes. Weight, on the otherhand does change with location.
So just imagine that you send a random object to the moon. The weight of the object will change hugely, but the mass of the object will not change at all. This is because the gravitational pull on the moon is not as strong as the gravitational pull on earth, causing the object to weigh less on the moon.
This diagram shows that the weight changes through different changes of gravity.
When the elevator is stationary and staying still, the pull of gravity on them an inside is normal, therefore he weighs the same as he would on the ground.
When the elevator is accelerating upward, the pull of gravity if trying to pull the man inside the elevator back down to earth causing the man to weigh more than his usual weight.
When the elevator is accelerating downwards, the man inside feels lighter and his weight his less because he is giving in with the pull of gravity.
If the elevator cable snaps and the man is in free-fall, the man will have no weight at all because he is falling.


Do You Weigh Less When the Moon is Above You?
Everything in the universe that has mass, has gravity. It’s easy to understand that the Earth has gravity and pulls on us all day every day. It’s just as easy to understand that the Moon and the planets and the Sun have gravity too, and they are all pulling on us.It’s much harder to understand that every person on Earth has gravity too. You exert a force on the Earth, and on every other human. You also exert a force on every rock, tree, and creature that roams the Earth, and they all exert a force on you. The only problem is that you have such a small mass compared to the Earth, the gravitational force you exert is very tiny.
Some people ask me “Why don’t we feel the gravity from a mountain?”
For one, it’s because the Earth itself weighs much more than the mountain, so the mountain has little gravity, even though its huge. The other reason is that the gravity exerted by any spherically distributed mass (like the Earth) is the same as if all the mass was at the centre of the object.

What about the Moon? The Moon is big, and it’s relatively close to us! What if the Moon is overhead? Would it’s pull make us lighter? Would it make us heavier if it was on the other side of the Earth?
Let’s figure it out!
Isaac Newton was the guy who figured out gravity and how it works. He came up with an equation to measure the gravitational force between any two objects:
You, standing on the Earth!
The Earth weighs 5.72×1024 Kg, and the distance between you and the centre of the Earth (where you feel the pull of gravity) is r = 6,371,000 m. Throw all this into the equation above and we find that the force exerted on you from the Earth is:
F = 9.4 x M you
So ~9.4 times your mass. This is why more massive things are harder
to lift. The actual answer, measured by humans since the dawn of
science, is 9.81 times your mass. It’s different than our calculation
due to the fact that the Earth doesn’t have the same density everywhere
(some of it is water, rock, etc). If you divide this by your mass you
get the Earth’s acceleration due to gravity, independent of mass:
g = 9.81 m/s2
All things accelerate at the same rate, no matter how heavy they are.
A feather falls as fast as a bowling ball. the only difference is
that the bowling ball will hurt a lot more if it falls on you. Okay so let’s look at the Moon:
The Earth and Moon are orbiting a point between them, their center of mass. because the Earth is more massive, the center of mass of the Earth Moon system is inside the Earth, about 1,700 Km from the surface. This means the Earth ‘wobbles’ as the Moon orbits.

F = m*v2 / r
You and the Earth are both in free fall around the center of mass.
But because you are stationary on the Earth, the ground pushes on you
and you perceive the Earth’s gravity.“But I thought ocean tides happen because of the Moon’s Gravity!”
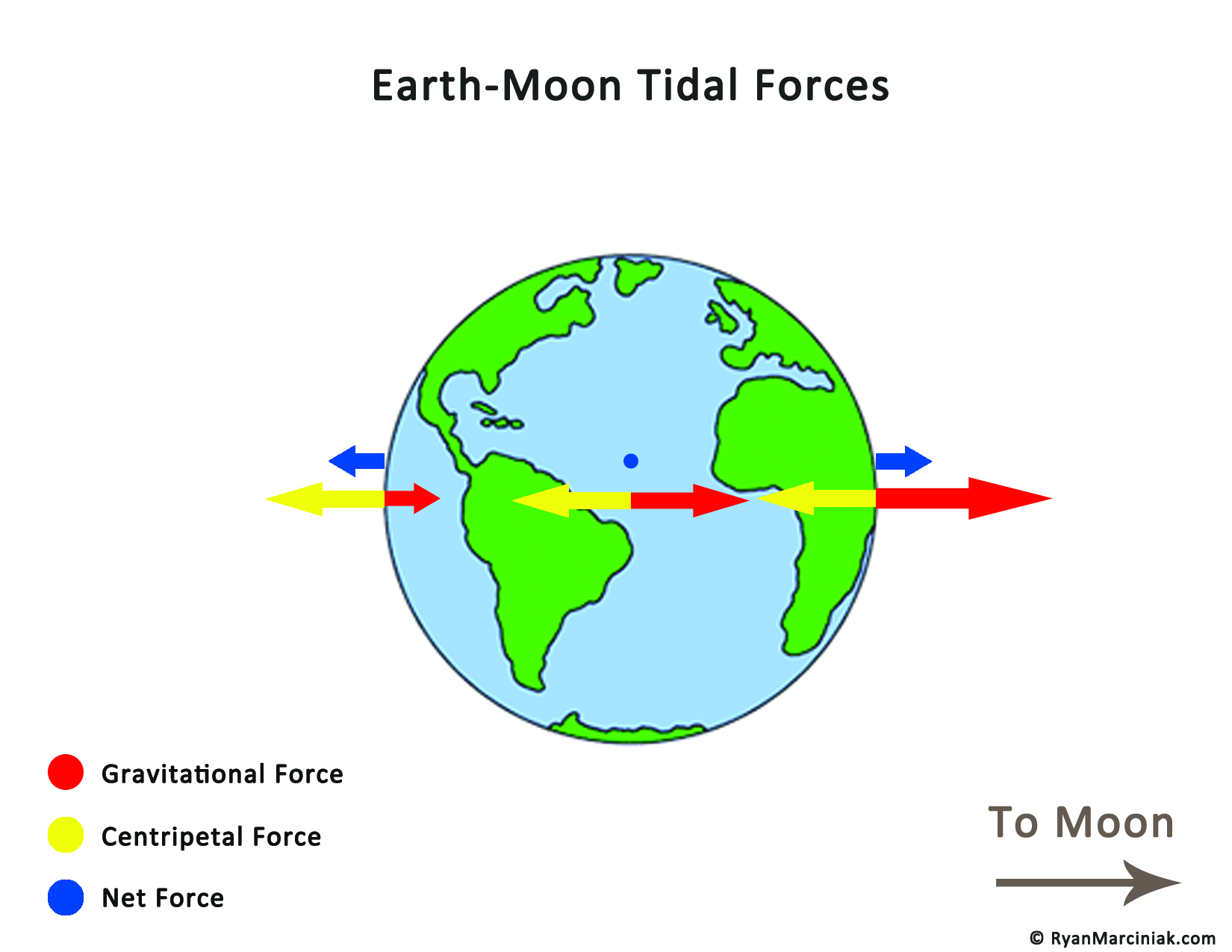
They do! When we talk about the interaction of two large bodies, such as the Moon’s gravitational influence on the Earth, we need to discuss the tidal force.
Because the Earth is a large solid body, it’s entire mass orbits at the same speed. This is the key to tidal forces. The Centripetal force of the Earth is the same across it’s entire diameter, but because gravity depends on distance, the side of the Earth facing the Moon feels more gravity that the side facing away. This results in the tidal force on both sides of the Earth, pointing away from the center.
This means that you weigh less when the Moon is above you AND when the Moon is on the opposite side of the Earth from you. In both cases, your weight changes by (almost) the same amount. Here is a map of the tidal force from different points along the Earth’s surface.

So how strong is the tidal force? How much does our weight change because of the Moon?
(Note: If you don’t want to see the math, scroll down to see the answer)To find the tidal force from the moon, we will compare the Moon’s acceleration due to gravity acting at the edge of the Earth, to that at the center of the Earth. Because we are connected to the Earth, we have the exact same centripetal force, and so we should feel the tidal force acting on us too.
For the side facing the Moon:
Since Force = Mass x Acceleration, we can take Newton’s law of Gravitation from above and divide both sides by mass to get the following formula for acceleration due to gravity.
a = G * M / r2
For the edge of the Earth in this case, r
will be the Earth-Moon distance (which is measured from the center of
the Earth to the center of the Moon) minus the radius of Earth. When we
do the calculation for the far side, we will add the Earth’s radius to
the Earth-Moon distance.
So if the Earth-Moon distance is R, and Earth’s radius is rEarth,
anear = G * Mmoon / (R – rEarth)2 – G * Mmoon / R2
The Earth-Moon distance is roughly 380,000,000 m, the Earth’s radius is 6,371,000 m, G is G = 6.67 x 10-11N(m/kg)2, and the Moon has a mass of 7.348 x 1022 Kg. The calculation gives us:
anear = 0.00000117 m/s2
A very tiny acceleration.
For the side opposite the Moon:
For the edge of the Earth this time, r will be the Earth-Moon distance plus the
radius of Earth. Using the same equation as last time with the new
distances, and subtracting the gravity at the edge from that at the
center:
afar = G * Mmoon / R2 – G * Mmoon / (R + rEarth)2
With the same numbers as before, the calculation gives us:
afar = 0.00000111 m/s2
A slightly tinier acceleration.
So the tidal force is a little bit stronger
on the Moon-facing side, but only by about 5%. Now let’s compare this
to the acceleration due to gravity on the Earth from above, 9.81 m/s2.
The gravity you feel from the Moon is just over 1 one-millionth of the gravity you feel from Earth, which means if the Moon is above your head or on the opposite side of Earth, your weight will only drop by a millionth of a Kilogram.

It’s pretty obvious now that the Moon’s
gravity won’t give the slightest noticeable effect, and with the Sun and
other planets being much further away, their effect is tiny too. The
gravity of the Solar System just doesn’t affect us because gravity
decreases with the square of the distance. Something that is twice as
far from Earth feels only 1/4 of the gravity. So let’s ramp it up a bit.
Is there a place in the Solar System where we would notice a
difference?
For this one we are going to travel to
Jupiter’s Moon Io. Io is the closest of the Galilean moons, and Jupiter
is the most massive planet in the solar system. Will we get a
different result?
Again the tidal force will make us lighter
if Jupiter is overhead or on the opposite side, just as with the Earth
and the Moon, but will it make a noticeable difference?
Using Jupiter, the largest planet in the Solar System, and Io, its closest Moon, will Jupiter’s tides make us lighter?

This time the masses are different, as are the distances. We are going to look at how much we weigh on Io, and how much the tidal force is. Start with the general information we will need:
Mass of Io = 8.93 x 1022 Kg
Mass of Jupiter = 1.898 x 1027 Kg
Radius of Io = 1,821,600 m
Jupiter to Io distance (centre to centre) = R = 421,700,000 m
Acceleration due to gravity on Io
Let’s forget Jupiter for a second and see what the acceleration due to gravity is on Io:
aIo = G * MIo / (rIo)2
Using the radius and mass of Io from above gives us:
aIo = 1.796 m/s2
Io has a lot less gravity than the Earth, since it’s much smaller.
You would weigh around 1/6 of your weight on Earth (similar to the Moon
actually).Tidal force due to Jupiter’s gravity
Again we will look at the near and far sides of Io, just as we did when we were standing on Earth. Only this time, it’s mighty Jupiter creating the tides.
For the side with Jupiter above us:
Just as with the Earth and Moon, we will
have to find the difference between the gravity at the edge and the
gravity at the centre, so we use:
anear = G * MJup / (R – rIo)2 – G * MJup / R2
Where R is the distance between Io and Jupiter. Doing the calculation, we get:
anear = 0.0062 m/s2
For the side opposite Jupiter:
This time, as before, we add the radius of Io to the Jupiter-Io distance to get the correct measure of the tides:
afar = G * MJup / R2 – G * MJup / (R + rIo)2
Where R is the distance between Io and Jupiter. Doing the calculation, we get:
anear = 0.0061 m/s2
A very interesting result!This means that even with the powerful gravity of Jupiter, your weight on Io will only vary by one ten-thousanth of a Kilogram!
This is because the tidal force really depends on the distance between the objects. As the objects get closer together, the tidal forces increase substantially! If the Moon was twice as close to us as it is now, the tidal forces it exerts on the Earth would increase by a factor of 8!Even on Io, with Jupiter’s massive gravity, the tides are small because Io is far enough away. If the tides were much stronger, Io would have easily been ripped apart by Jupiter. The minimum distance for a satellite to remain intact is called the roche limit. After this point the tidal force is greater than the satellite’s own gravity, and it is pulled apart.
Io itself is a volcanic world due to tidal forces, but it’s not entirely Jupiter’s fault. The other Galilean Moons of Jupiter contribute to Io having an eccentric orbit, causing Io’s orbital distance to vary. This creates variations in the tidal force it feels from Jupiter, and the changing tides cause Io’s crust to be pushed and pulled regularly, creating friction in the crust and a massive amount of heat that manifests itself as volcanic activity.



Weight
For an object in free fall, so that gravity is the only force acting on it, then the expression for weight follows from Newton's second law.

Data can be entered into any of the boxes below. Then click outside the box to update the other quantities.

The
kilogram is the SI unit of mass and it the almost universally used
standard mass unit. The associated SI unit of force and weight is the
Newton, with 1 kilogram weighing 9.8 Newtons under standard conditions
on the Earth's surface. However, in the US common units, the pound is
the unit of force (and therefore weight).The pound is the widely used
unit for commerce. The use of the pound force constrains the mass unit
to an inconveniently large measuring unit called a "slug". The use of
this unit is discouraged, and the use of exclusively SI units for all
scientific work is strongly encouraged.  Weightlessness |













Tidak ada komentar:
Posting Komentar