XXX . XXX Antenna (radio)
In radio, an antenna is the interface between radio waves propagating through space and electric currents moving in metal conductors, used with a transmitter or receiver.[1] In transmission, a radio transmitter supplies an electric current to the antenna's terminals, and the antenna radiates the energy from the current as electromagnetic waves (radio waves). In reception, an antenna intercepts some of the power of an electromagnetic wave in order to produce an electric current at its terminals, that is applied to a receiver to be amplified. Antennas are essential components of all radio equipment, and are used in radio broadcasting, broadcast television, two-way radio, communications receivers, radar, cell phones, satellite communications and other devices.
An antenna is an array of conductors (elements), electrically connected to the receiver or transmitter. During transmission, the oscillating current applied to the antenna by a transmitter creates an oscillating electric field and magnetic field around the antenna elements. These time-varying fields radiate energy away from the antenna into space as a moving transverse electromagnetic field wave. Conversely, during reception, the oscillating electric and magnetic fields of an incoming radio wave exert force on the electrons in the antenna elements, causing them to move back and forth, creating oscillating currents in the antenna.
Antennas can be designed to transmit and receive radio waves in all horizontal directions equally (omnidirectional antennas), or preferentially in a particular direction (directional or high gain antennas). An antenna may include parasitic elements, parabolic reflectors or horns, which serve to direct the radio waves into a beam or other desired radiation pattern.
The first antennas were built in 1888 by German physicist Heinrich Hertz in his pioneering experiments to prove the existence of electromagnetic waves predicted by the theory of James Clerk Maxwell. Hertz placed dipole antennas at the focal point of parabolic reflectors for both transmitting and receiving and This now I call and project name is ( SWITCH X <----> SWITCH O ) .

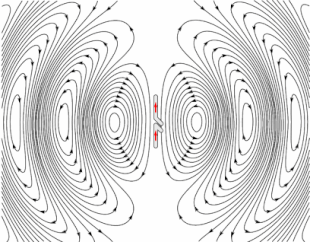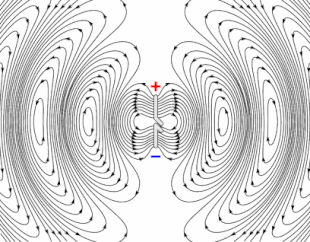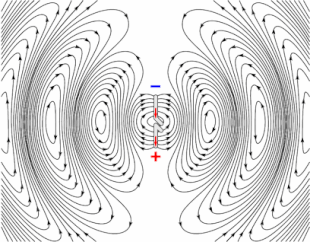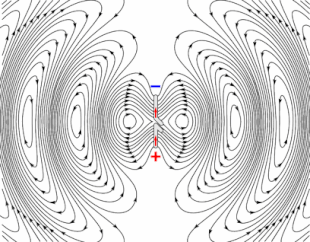
Animation of a half-wave dipole antenna transmitting radio waves, showing the electric field lines. The antenna in the center is two vertical metal rods, with an alternating current applied at its center from a radio transmitter (not shown). The voltage charges the two sides of the antenna alternately positive (+) and negative (−). Loops of electric field (black lines) leave the antenna and travel away at the speed of light; these are the radio waves.
Terminology
The words antenna and aerial are used interchangeably. Occasionally the term "aerial" is used to mean a wire antenna. The origin of the word antenna relative to wireless apparatus is attributed to Italian radio pioneer Guglielmo Marconi. In the summer of 1895, Marconi began testing his wireless system outdoors on his father's estate near Bologna and soon began to experiment with long wire "aerials" suspended from a pole. In Italian a tent pole is known as l'antenna centrale, and the pole with the wire was simply called l'antenna. Until then wireless radiating transmitting and receiving elements were known simply as terminals. Because of his prominence, Marconi's use of the word antenna spread among wireless researchers, and later to the general public.
Antenna may refer broadly to an entire assembly including support structure, enclosure (if any), etc. in addition to the actual functional components. Especially at microwave frequencies, a receiving antenna may include not only the actual electrical antenna but an integrated preamplifier or mixer.
Antennas are required by any radio receiver or transmitter to couple its electrical connection to the electromagnetic field[7]. Radio waves are electromagnetic waves which carry signals through the air (or through space) at the speed of light with almost no transmission loss. Radio transmitters and receivers are used to convey signals in broadcast (audio) radio, television, mobile telephones, Wi-Fi (WLAN) data networks, and remote control devices among many others. Radio waves are also used directly for measurements in radar[8], GPS, and radio astronomy. Transmitters and receivers require antennas, although these are sometimes hidden (such as the antenna inside an AM radio or inside a laptop computer equipped with Wi-Fi).
Antennas can be classified as omnidirectional, radiating energy approximately equally in all directions, or Directional, where energy radiates more along one direction than others. (Antennas are reciprocal, so the same effect occurs for reception of radio waves.) A completely uniform omnidirectional antenna is not physically possible. Many important antenna types have a uniform radiation pattern in the horizontal plane, but send little energy upward or downward. A "directional" antenna usually is intended to maximize its coupling to the electromagnetic field in the direction of the other station.
One example of omnidirectional antennas is the very common vertical antenna or whip antenna consisting of a metal rod. A dipole antenna is similar but consists of two such conductors extending in opposite directions. Dipoles are typically oriented horizontally in which case they are weakly directional: signals are reasonably well radiated toward or received from all directions with the exception of the direction along the conductor itself; this region is called the antenna blind cone or null.
Both the vertical and dipole antennas are simple in construction and relatively inexpensive. The dipole antenna, which is the basis for most antenna designs, is a balanced component, with equal but opposite voltages and currents applied at its two terminals through a balanced transmission line (or to a coaxial transmission line through a so-called balun). The vertical antenna, on the other hand, is a monopole antenna. It is typically connected to the inner conductor of a coaxial transmission line (or a matching network); the shield of the transmission line is connected to ground. In this way, the ground (or any large conductive surface) plays the role of the second conductor of a dipole, thereby forming a complete circuit. Since monopole antennas rely on a conductive ground, a so-called grounding structure may be employed to provide a better ground contact to the earth or which itself acts as a ground plane to perform that function regardless of (or in absence of) an actual contact with the earth.
Antennas more complex than the dipole or vertical designs are usually intended to increase the directivity and consequently the gain of the antenna. This can be accomplished in many different ways leading to a plethora of antenna designs. The vast majority of designs are fed with a balanced line (unlike a monopole antenna) and are based on the dipole antenna with additional components (or elements) which increase its directionality. Antenna "gain" in this instance describes the concentration of radiated power into a particular solid angle of space, as opposed to the spherically uniform radiation of the ideal radiator. The increased power in the desired direction is at the expense of that in the undesired directions. Power is conserved, and there is no net power increase over that delivered from the power source (the transmitter.)
For instance, a phased array consists of two or more simple antennas which are connected together through an electrical network. This often involves a number of parallel dipole antennas with a certain spacing. Depending on the relative phase introduced by the network, the same combination of dipole antennas can operate as a "broadside array" (directional normal to a line connecting the elements) or as an "end-fire array" (directional along the line connecting the elements). Antenna arrays may employ any basic (omnidirectional or weakly directional) antenna type, such as dipole, loop or slot antennas. These elements are often identical.
However a log-periodic dipole array consists of a number of dipole elements of different lengths in order to obtain a somewhat directional antenna having an extremely wide bandwidth: these are frequently used for television reception in fringe areas. The dipole antennas composing it are all considered "active elements" since they are all electrically connected together (and to the transmission line). On the other hand, a superficially similar dipole array, the Yagi-Uda Antenna (or simply "Yagi"), has only one dipole element with an electrical connection; the other so-called parasitic elements interact with the electromagnetic field in order to realize a fairly directional antenna but one which is limited to a rather narrow bandwidth. The Yagi antenna has similar looking parasitic dipole elements but which act differently due to their somewhat different lengths. There may be a number of so-called "directors" in front of the active element in the direction of propagation, and usually a single (but possibly more) "reflector" on the opposite side of the active element.
Greater directionality can be obtained using beam-forming techniques such as a parabolic reflector or a horn. Since high directivity in an antenna depends on it being large compared to the wavelength, narrow beams of this type are more easily achieved at UHF and microwave frequencies.
At low frequencies (such as AM broadcast), arrays of vertical towers are used to achieve directionality[9] and they will occupy large areas of land. For reception, a long Beverage antenna can have significant directivity. For non directional portable use, a short vertical antenna or small loop antenna works well, with the main design challenge being that of impedance matching. With a vertical antenna a loading coil at the base of the antenna may be employed to cancel the reactive component of impedance; small loop antennas are tuned with parallel capacitors for this purpose.
An antenna lead-in is the transmission line, or feed line, which connects the antenna to a transmitter or receiver. The "antenna feed" may refer to all components connecting the antenna to the transmitter or receiver, such as an impedance matching network in addition to the transmission line. In a so-called aperture antenna, such as a horn or parabolic dish, the "feed" may also refer to a basic antenna inside the entire system (normally at the focus of the parabolic dish or at the throat of a horn) which could be considered the one active element in that antenna system. A microwave antenna may also be fed directly from a waveguide in place of a (conductive) transmission line.
An antenna counterpoise, or ground plane, is a structure of conductive material which improves or substitutes for the ground. It may be connected to or insulated from the natural ground. In a monopole antenna, this aids in the function of the natural ground, particularly where variations (or limitations) of the characteristics of the natural ground interfere with its proper function. Such a structure is normally connected to the return connection of an unbalanced transmission line such as the shield of a coaxial cable.
An electromagnetic wave refractor in some aperture antennas is a component which due to its shape and position functions to selectively delay or advance portions of the electromagnetic wavefront passing through it. The refractor alters the spatial characteristics of the wave on one side relative to the other side. It can, for instance, bring the wave to a focus or alter the wave front in other ways, generally in order to maximize the directivity of the antenna system. This is the radio equivalent of an optical lens.
An antenna coupling network is a passive network (generally a combination of inductive and capacitive circuit elements) used for impedance matching in between the antenna and the transmitter or receiver. This may be used to improve the standing wave ratio in order to minimize losses in the transmission line and to present the transmitter or receiver with a standard resistive impedance that it expects to see for optimum operation.
Reciprocity
It is a fundamental property of antennas that the electrical characteristics of an antenna described in the next section, such as gain, radiation pattern, impedance, bandwidth, resonant frequency and polarization, are the same whether the antenna is transmitting or receiving. For example, the "receiving pattern" (sensitivity as a function of direction) of an antenna when used for reception is identical to the radiation pattern of the antenna when it is driven and functions as a radiator. This is a consequence of the reciprocity theorem of electromagnetics. Therefore, in discussions of antenna properties no distinction is usually made between receiving and transmitting terminology, and the antenna can be viewed as either transmitting or receiving, whichever is more convenient.
A necessary condition for the aforementioned reciprocity property is that the materials in the antenna and transmission medium are linear and reciprocal. Reciprocal (or bilateral) means that the material has the same response to an electric current or magnetic field in one direction, as it has to the field or current in the opposite direction. Most materials used in antennas meet these conditions, but some microwave antennas use high-tech components such as isolators and circulators, made of nonreciprocal materials such as ferrite. These can be used to give the antenna a different behavior on receiving than it has on transmitting,which can be useful in applications like radar.
Characteristics
Antennas are characterized by a number of performance measures which a user would be concerned with in selecting or designing an antenna for a particular application. Chief among these relate to the directional characteristics (as depicted in the antenna's radiation pattern) and the resulting gain. Even in omnidirectional (or weakly directional) antennas, the gain can often be increased by concentrating more of its power in the horizontal directions, sacrificing power radiated toward the sky and ground. The antenna's power gain (or simply "gain") also takes into account the antenna's efficiency, and is often the primary figure of merit.
Resonant antennas are expected to be used around a particular resonant frequency; an antenna must therefore be built or ordered to match the frequency range of the intended application. A particular antenna design will present a particular feedpoint impedance. While this may affect the choice of an antenna, an antenna's impedance can also be adapted to the desired impedance level of a system using a matching network while maintaining the other characteristics (except for a possible loss of efficiency).
Although these parameters can be measured in principle, such measurements are difficult and require very specialized equipment. Beyond tuning a transmitting antenna using an SWR meter, the typical user will depend on theoretical predictions based on the antenna design or on claims of a vendor.
An antenna transmits and receives radio waves with a particular polarization which can be reoriented by tilting the axis of the antenna in many (but not all) cases. The physical size of an antenna is often a practical issue, particularly at lower frequencies (longer wavelengths). Highly directional antennas need to be significantly larger than the wavelength. Resonant antennas usually use a linear conductor (or element), or pair of such elements, each of which is about a quarter of the wavelength in length (an odd multiple of quarter wavelengths will also be resonant). Antennas that are required to be small compared to the wavelength sacrifice efficiency and cannot be very directional. At higher frequencies (UHF, microwaves) trading off performance to obtain a smaller physical size is usually not required.
Resonant antennas
The majority of antenna designs are based on the resonance principle. This relies on the behaviour of moving electrons, which reflect off surfaces where the dielectric constant changes, in a fashion similar to the way light reflects when optical properties change. In these designs, the reflective surface is created by the end of a conductor, normally a thin metal wire or rod, which in the simplest case has a feed point at one end where it is connected to a transmission line. The conductor, or element, is aligned with the electrical field of the desired signal, normally meaning it is perpendicular to the line from the antenna to the source (or receiver in the case of a broadcast antenna).
The radio signal's electrical component induces a voltage in the conductor. This causes an electrical current to begin flowing in the direction of the signal's instantaneous field. When the resulting current reaches the end of the conductor, it reflects, which is equivalent to a 180 degree change in phase. If the conductor is 1⁄4 of a wavelength long, current from the feed point will undergo 90 degree phase change by the time it reaches the end of the conductor, reflect through 180 degrees, and then another 90 degrees as it travels back. That means it has undergone a total 360 degree phase change, returning it to the original signal. The current in the element thus adds to the current being created from the source at that instant. This process creates a standing wave in the conductor, with the maximum current at the feed.[13]
The ordinary half-wave dipole is probably the most widely used antenna design. This consists of two 1⁄4-wavelength elements arranged end-to-end, and lying along essentially the same axis (or collinear), each feeding one side of a two-conductor transmission wire. The physical arrangement of the two elements places them 180 degrees out of phase, which means that at any given instant one of the elements is driving current into the transmission line while the other is pulling it out. The monopole antenna is essentially one half of the half-wave dipole, a single 1⁄4-wavelength element with the other side connected to ground or an equivalent ground plane (or counterpoise). Monopoles, which are one-half the size of a dipole, are common for long-wavelength radio signals where a dipole would be impractically large. Another common design is the folded dipole, which is essentially two dipoles placed side-by-side and connected at their ends to make a single one-wavelength antenna.
The standing wave forms with this desired pattern at the design frequency, f0, and antennas are normally designed to be this size. However, feeding that element with 3f0 (whose wavelength is 1⁄3 that of f0) will also lead to a standing wave pattern. Thus, an antenna element is also resonant when its length is 3⁄4 of a wavelength. This is true for all odd multiples of 1⁄4 wavelength. This allows some flexibility of design in terms of antenna lengths and feed points. Antennas used in such a fashion are known to be harmonically operated.
Current and voltage distribution
The quarter-wave elements imitate a series-resonant electrical element due to the standing wave present along the conductor. At the resonant frequency, the standing wave has a current peak and voltage node (minimum) at the feed. In electrical terms, this means the element has minimum reactance, generating the maximum current for minimum voltage. This is the ideal situation, because it produces the maximum output for the minimum input, producing the highest possible efficiency. Contrary to an ideal (lossless) series-resonant circuit, a finite resistance remains (corresponding to the relatively small voltage at the feed-point) due to the antenna's radiation resistance as well as any actual electrical losses.
Recall that a current will reflect when there are changes in the electrical properties of the material. In order to efficiently send the signal into the transmission line, it is important that the transmission line has the same impedance as the elements, otherwise some of the signal will be reflected back into the antenna. This leads to the concept of impedance matching, the design of the overall system of antenna and transmission line so the impedance is as close as possible, thereby reducing these losses. Impedance matching between antennas and transmission lines is commonly handled through the use of a balun, although other solutions are also used in certain roles. An important measure of this basic concept is the standing wave ratio, which measures the magnitude of the reflected signal.
Consider a half-wave dipole designed to work with signals 1 m wavelength, meaning the antenna would be approximately 50 cm across. If the element has a length-to-diameter ratio of 1000, it will have an inherent resistance of about 63 ohms. Using the appropriate transmission wire or balun, we match that resistance to ensure minimum signal loss. Feeding that antenna with a current of 1 ampere will require 63 volts of RF, and the antenna will radiate 63 watts (ignoring losses) of radio frequency power. Now consider the case when the antenna is fed a signal with a wavelength of 1.25 m; in this case the reflected current would arrive at the feed out-of-phase with the signal, causing the net current to drop while the voltage remains the same. Electrically this appears to be a very high impedance. The antenna and transmission line no longer have the same impedance, and the signal will be reflected back into the antenna, reducing output. This could be addressed by changing the matching system between the antenna and transmission line, but that solution only works well at the new design frequency.
The end result is that the resonant antenna will efficiently feed a signal into the transmission line only when the source signal's frequency is close to that of the design frequency of the antenna, or one of the resonant multiples. This makes resonant antenna designs inherently narrowband, and they are most commonly used with a single target signal. They are particularly common on radar systems, where the same antenna is used for both broadcast and reception, or for radio and television broadcasts, where the antenna is working with a single frequency. They are less commonly used for reception where multiple channels are present, in which case additional modifications are used to increase the bandwidth, or entirely different antenna designs are used.
Electrically short antennas
It is possible to use simple impedance matching techniques to allow the use of monopole or dipole antennas substantially shorter than the ¼ or ½ wavelength, respectively, at which they are resonant. As these antennas are made shorter (for a given frequency) their impedance becomes dominated by a series capacitive (negative) reactance; by adding a series inductance with the opposite (positive) reactance – a so-called loading coil – the antenna's reactance may be cancelled leaving only a pure resistance. Sometimes the resulting (lower) electrical resonant frequency of such a system (antenna plus matching network) is described using the concept of electrical length, so an antenna used at a lower frequency than its resonant frequency is called an electrically short antenna .
For example, at 30 MHz (10 m wavelength) a true resonant ¼ wavelength monopole would be almost 2.5 meters long, and using an antenna only 1.5 meters tall would require the addition of a loading coil. Then it may be said that the coil has lengthened the antenna to achieve an electrical length of 2.5 meters. However, the resulting resistive impedance achieved will be quite a bit lower than that of a true ¼ wave (resonant) monopole, often requiring further impedance matching (a transformer) to the desired transmission line. For ever shorter antennas (requiring greater "electrical lengthening") the radiation resistance plummets (approximately according to the square of the antenna length), so that the mismatch due to a net reactance away from the electrical resonance worsens. Or one could as well say that the equivalent resonant circuit of the antenna system has a higher Q factor and thus a reduced bandwidth, which can even become inadequate for the transmitted signal's spectrum. Resistive losses due to the loading coil, relative to the decreased radiation resistance, entail a reduced electrical efficiency, which can be of great concern for a transmitting antenna, but bandwidth is the major factor that sets the size of antennas at 1 MHz and lower frequencies.
Arrays and reflectors
The amount of signal received from a distant transmission source is essentially geometric in nature due to the inverse-square law, and this leads to the concept of effective area. This measures the performance of an antenna by comparing the amount of power it generates to the amount of power in the original signal, measured in terms of the signal's power density in Watts per square metre. A half-wave dipole has an effective area of 0.13 2. If more performance is needed, one cannot simply make the antenna larger. Although this would intercept more energy from the signal, due to the considerations above, it would decrease the output significantly due to it moving away from the resonant length. In roles where higher performance is needed, designers often use multiple elements combined together.
Returning to the basic concept of current flows in a conductor, consider what happens if a half-wave dipole is not connected to a feed point, but instead shorted out. Electrically this forms a single 1⁄2-wavelength element. But the overall current pattern is the same; the current will be zero at the two ends, and reach a maximum in the center. Thus signals near the design frequency will continue to create a standing wave pattern. Any varying electrical current, like the standing wave in the element, will radiate a signal. In this case, aside from resistive losses in the element, the rebroadcast signal will be significantly similar to the original signal in both magnitude and shape. If this element is placed so its signal reaches the main dipole in-phase, it will reinforce the original signal, and increase the current in the dipole. Elements used in this way are known as passive elements.
A Yagi-Uda array uses passive elements to greatly increase gain. It is built along a support boom that is pointed toward the signal, and thus sees no induced signal and does not contribute to the antenna's operation. The end closer to the source is referred to as the front. Near the rear is a single active element, typically a half-wave dipole or folded dipole. Passive elements are arranged in front (directors) and behind (reflectors) the active element along the boom. The Yagi has the inherent quality that it becomes increasingly directional, and thus has higher gain, as the number of elements increases. However, this also makes it increasingly sensitive to changes in frequency; if the signal frequency changes, not only does the active element receive less energy directly, but all of the passive elements adding to that signal also decrease their output as well and their signals no longer reach the active element in-phase.
It is also possible to use multiple active elements and combine them together with transmission lines to produce a similar system where the phases add up to reinforce the output. The antenna array and very similar reflective array antenna consist of multiple elements, often half-wave dipoles, spaced out on a plane and wired together with transmission lines with specific phase lengths to produce a single in-phase signal at the output. The log-periodic antenna is a more complex design that uses multiple in-line elements similar in appearance to the Yagi-Uda but using transmission lines between the elements to produce the output.
Reflection of the original signal also occurs when it hits an extended conductive surface, in a fashion similar to a mirror. This effect can also be used to increase signal through the use of a reflector, normally placed behind the active element and spaced so the reflected signal reaches the element in-phase. Generally the reflector will remain highly reflective even if it is not solid; gaps less than 1⁄10 generally have little effect on the outcome. For this reason, reflectors often take the form of wire meshes or rows of passive elements, which makes them lighter and less subject to wind-load effects, of particular importance when mounted at higher elevations with respect to the surrounding structures. The parabolic reflector is perhaps the best known example of a reflector-based antenna, which has an effective area far greater than the active element alone.
Bandwidth
Although a resonant antenna has a purely resistive feed-point impedance at a particular frequency, many (if not most) applications require using an antenna over a range of frequencies. The frequency range or bandwidth over which an antenna functions well can be very wide (as in a log-periodic antenna) or narrow (in a resonant antenna); outside this range the antenna impedance becomes a poor match to the transmission line and transmitter (or receiver). Also in the case of the Yagi-Uda and other end-fire arrays, use of the antenna well away from its design frequency affects its radiation pattern, reducing its directive gain; the usable bandwidth is then limited regardless of impedance matching.
Except for the latter concern, the resonant frequency of an antenna system can always be altered by adjusting a suitable matching network. This is most efficiently accomplished using a matching network at the site of the antenna, since simply adjusting a matching network at the transmitter (or receiver) would leave the transmission line with a poor standing wave ratio.
Instead, it is often desired to have an antenna whose impedance does not vary so greatly over a certain bandwidth. It turns out that the amount of reactance seen at the terminals of a resonant antenna when the frequency is shifted, say, by 5%, depends very much on the diameter of the conductor used. A long thin wire used as a half-wave dipole (or quarter wave monopole) will have a reactance significantly greater than the resistive impedance it has at resonance, leading to a poor match and generally unacceptable performance. Making the element using a tube of a diameter perhaps 1/50 of its length, however, results in a reactance at this altered frequency which is not so great, and a much less serious mismatch and effect on the antenna's net performance. Thus rather thick tubes are often used for the elements; these also have reduced parasitic resistance (loss).
Rather than just using a thick tube, there are similar techniques used to the same effect such as replacing thin wire elements with cages to simulate a thicker element. This widens the bandwidth of the resonance. On the other hand, it is desired for amateur radio antennas to operate at several bands which are widely separated from each other (but not in between). This can often be accomplished simply by connecting elements resonant at those different frequencies in parallel. Most of the transmitter's power will flow into the resonant element while the others present a high (reactive) impedance, thus drawing little current from the same voltage. Another popular solution uses so-called traps consisting of parallel resonant circuits which are strategically placed in breaks along each antenna element. When used at one particular frequency band the trap presents a very high impedance (parallel resonance) effectively truncating the element at that length, making it a proper resonant antenna. At a lower frequency the trap allows the full length of the element to be employed, albeit with a shifted resonant frequency due to the inclusion of the trap's net reactance at that lower frequency.
The bandwidth characteristics of a resonant antenna element can be characterized according to its Q, just as one uses to characterize the sharpness of an L-C resonant circuit. A common mistake is to assume that there is an advantage in an antenna having a high Q (the so-called "quality factor"). In the context of electronic circuitry a low Q generally signifies greater loss (due to unwanted resistance) in a resonant L-C circuit, and poorer receiver selectivity. However this understanding does not apply to resonant antennas where the resistance involved is the radiation resistance, a desired quantity which removes energy from the resonant element in order to radiate it (the purpose of an antenna, after all!). The Q of an L-C-R circuit is defined as the ratio of the inductor's (or capacitor's) reactance to the resistance, so for a certain radiation resistance (the radiation resistance at resonance does not vary greatly with diameter) the greater reactance off-resonance causes the poorer bandwidth of an antenna employing a very thin conductor. The Q of such a narrowband antenna can be as high as 15. On the other hand, the reactance at the same off-resonant frequency of one using thick elements is much less, consequently resulting in a Q as low as 5. These two antennas may perform equivalently at the resonant frequency, but the second antenna will perform over a bandwidth 3 times as wide as the antenna consisting of a thin conductor.
Antennas for use over much broader frequency ranges are achieved using further techniques. Adjustment of a matching network can, in principle, allow for any antenna to be matched at any frequency. Thus the loop antenna built into most AM broadcast (medium wave) receivers has a very narrow bandwidth, but is tuned using a parallel capacitance which is adjusted according to the receiver tuning. On the other hand, log-periodic antennas are not resonant at any frequency but can be built to attain similar characteristics (including feedpoint impedance) over any frequency range. These are therefore commonly used (in the form of directional log-periodic dipole arrays) as television antennas.
Gain
Gain is a parameter which measures the degree of directivity of the antenna's radiation pattern. A high-gain antenna will radiate most of its power in a particular direction, while a low-gain antenna will radiate over a wider angle. The antenna gain, or power gain of an antenna is defined as the ratio of the intensity (power per unit surface area) radiated by the antenna in the direction of its maximum output, at an arbitrary distance, divided by the intensity radiated at the same distance by a hypothetical isotropic antenna which radiates equal power in all directions. This dimensionless ratio is usually expressed logarithmically in decibels, these units are called "decibels-isotropic" (dBi)
A second unit used to measure gain is the ratio of the power radiated by the antenna to the power radiated by a half-wave dipole antenna ; these units are called "decibels-dipole" (dBd)
Since the gain of a half-wave dipole is 2.15 dBi and the logarithm of a product is additive, the gain in dBi is just 2.15 decibels greater than the gain in dBd
High-gain antennas have the advantage of longer range and better signal quality, but must be aimed carefully at the other antenna. An example of a high-gain antenna is a parabolic dish such as a satellite television antenna. Low-gain antennas have shorter range, but the orientation of the antenna is relatively unimportant. An example of a low-gain antenna is the whip antenna found on portable radios and cordless phones. Antenna gain should not be confused with amplifier gain, a separate parameter measuring the increase in signal power due to an amplifying device.
Effective area or aperture
The effective area or effective aperture of a receiving antenna expresses the portion of the power of a passing electromagnetic wave which it delivers to its terminals, expressed in terms of an equivalent area. For instance, if a radio wave passing a given location has a flux of 1 pW / m2 (10−12 watts per square meter) and an antenna has an effective area of 12 m2, then the antenna would deliver 12 pW of RF power to the receiver (30 microvolts rms at 75 ohms). Since the receiving antenna is not equally sensitive to signals received from all directions, the effective area is a function of the direction to the source.
Due to reciprocity (discussed above) the gain of an antenna used for transmitting must be proportional to its effective area when used for receiving. Consider an antenna with no loss, that is, one whose electrical efficiency is 100%. It can be shown that its effective area averaged over all directions must be equal to λ2/4π, the wavelength squared divided by 4π. Gain is defined such that the average gain over all directions for an antenna with 100% electrical efficiency is equal to 1. Therefore, the effective area Aeff in terms of the gain G in a given direction is given by:
For an antenna with an efficiency of less than 100%, both the effective area and gain are reduced by that same amount. Therefore, the above relationship between gain and effective area still holds. These are thus two different ways of expressing the same quantity. Aeff is especially convenient when computing the power that would be received by an antenna of a specified gain, as illustrated by the above example.
Radiation pattern
The radiation pattern of an antenna is a plot of the relative field strength of the radio waves emitted by the antenna at different angles. It is typically represented by a three-dimensional graph, or polar plots of the horizontal and vertical cross sections. The pattern of an ideal isotropic antenna, which radiates equally in all directions, would look like a sphere. Many nondirectional antennas, such as monopoles and dipoles, emit equal power in all horizontal directions, with the power dropping off at higher and lower angles; this is called an omnidirectional pattern and when plotted looks like a torus or donut.
The radiation of many antennas shows a pattern of maxima or "lobes" at various angles, separated by "nulls", angles where the radiation falls to zero. This is because the radio waves emitted by different parts of the antenna typically interfere, causing maxima at angles where the radio waves arrive at distant points in phase, and zero radiation at other angles where the radio waves arrive out of phase. In a directional antenna designed to project radio waves in a particular direction, the lobe in that direction is designed larger than the others and is called the "main lobe". The other lobes usually represent unwanted radiation and are called "sidelobes". The axis through the main lobe is called the "principal axis" or "boresight axis".
Field regions
The space surrounding an antenna can be divided into three concentric regions: the reactive near-field (also called the inductive near-field), the radiating near-field (Fresnel region) and the far-field (Fraunhofer) regions. These regions are useful to identify the field structure in each, although there are no precise boundaries.
The far-field region is far enough from the antenna to ignore its size and shape: It can be assumed that the electromagnetic wave is purely a radiating plane wave (electric and magnetic fields are in phase and perpendicular to each other and to the direction of propagation). This simplifies the mathematical analysis of the radiated field.
Impedance
As an electro-magnetic wave travels through the different parts of the antenna system (radio, feed line, antenna, free space) it may encounter differences in impedance (E/H, V/I, etc.). At each interface, depending on the impedance match, some fraction of the wave's energy will reflect back to the source, forming a standing wave in the feed line. The ratio of maximum power to minimum power in the wave can be measured and is called the standing wave ratio (SWR). A SWR of 1:1 is ideal. A SWR of 1.5:1 is considered to be marginally acceptable in low power applications where power loss is more critical, although an SWR as high as 6:1 may still be usable with the right equipment. Minimizing impedance differences at each interface (impedance matching) will reduce SWR and maximize power transfer through each part of the antenna system.
Complex impedance of an antenna is related to the electrical length of the antenna at the wavelength in use. The impedance of an antenna can be matched to the feed line and radio by adjusting the impedance of the feed line, using the feed line as an impedance transformer. More commonly, the impedance is adjusted at the load (see below) with an antenna tuner, a balun, a matching transformer, matching networks composed of inductors and capacitors, or matching sections such as the gamma match.
Efficiency
Efficiency of a transmitting antenna is the ratio of power actually radiated (in all directions) to the power absorbed by the antenna terminals. The power supplied to the antenna terminals which is not radiated is converted into heat. This is usually through loss resistance in the antenna's conductors, but can also be due to dielectric or magnetic core losses in antennas (or antenna systems) using such components. Such loss effectively robs power from the transmitter, requiring a stronger transmitter in order to transmit a signal of a given strength.
For instance, if a transmitter delivers 100 W into an antenna having an efficiency of 80%, then the antenna will radiate 80 W as radio waves and produce 20 W of heat. In order to radiate 100 W of power, one would need to use a transmitter capable of supplying 125 W to the antenna. Antenna efficiency is separate from impedance matching, which may also reduce the amount of power radiated using a given transmitter. If an SWR meter reads 150 W of incident power and 50 W of reflected power, that means that 100 W have actually been absorbed by the antenna (ignoring transmission line losses). How much of that power has actually been radiated cannot be directly determined through electrical measurements at (or before) the antenna terminals, but would require (for instance) careful measurement of field strength. The loss resistance and efficiency of an antenna can be calculated.
loss resistance will generally affect the feedpoint impedance, adding to its resistive component. That resistance will consist of the sum of the radiation resistance Rr and the loss resistance Rloss. If a current I is delivered to the terminals of an antenna, then a power of I2Rr will be radiated and a power of I2Rloss will be lost as heat. Therefore, the efficiency of an antenna is equal to Rr / (Rr + Rloss). Only the total resistance Rr + Rloss can be directly measured.
According to reciprocity, the efficiency of an antenna used as a receiving antenna is identical to the efficiency as defined above. The power that an antenna will deliver to a receiver (with a proper impedance match) is reduced by the same amount. In some receiving applications, the very inefficient antennas may have little impact on performance. At low frequencies, for example, atmospheric or man-made noise can mask antenna inefficiency. For example, CCIR Rep. 258-3 indicates man-made noise in a residential setting at 40 MHz is about 28 dB above the thermal noise floor. Consequently, an antenna with a 20 dB loss (due to inefficiency) would have little impact on system noise performance. The loss within the antenna will affect the intended signal and the noise/interference identically, leading to no reduction in signal to noise ratio (SNR).
Antennas which are not a good fraction of a wavelength in size are inevitably inefficient due to their small radiation resistance. AM broadcast radios include a small loop antenna for reception which has an extremely poor efficiency. This has little effect on the receiver's performance, but simply requires greater amplification by the receiver's electronics. Contrast this tiny component to the massive and very tall towers used at AM broadcast stations for transmitting at the very same frequency, where every percentage point of reduced antenna efficiency entails a substantial cost.
The definition of antenna gain or power gain already includes the effect of the antenna's efficiency. Therefore, if one is trying to radiate a signal toward a receiver using a transmitter of a given power, one need only compare the gain of various antennas rather than considering the efficiency as well. This is likewise true for a receiving antenna at very high (especially microwave) frequencies, where the point is to receive a signal which is strong compared to the receiver's noise temperature. However, in the case of a directional antenna used for receiving signals with the intention of rejecting interference from different directions, one is no longer concerned with the antenna efficiency, as discussed above. In this case, rather than quoting the antenna gain, one would be more concerned with the directive gain which does not include the effect of antenna (in)efficiency. The directive gain of an antenna can be computed from the published gain divided by the antenna's efficiency.
Polarization
The polarization of an antenna refers to the orientation of the electric field (E-plane) of the radio wave with respect to the Earth's surface and is determined by the physical structure of the antenna and by its orientation. This is distinct from the antenna's directionality. Thus, a simple straight wire antenna will have one polarization when mounted vertically, and a different polarization when mounted horizontally. As a transverse wave, the magnetic field of a radio wave is at right angles to that of the electric field, but by convention, talk of an antenna's "polarization" is understood to refer to the direction of the electric field.
Reflections generally affect polarization. For radio waves, one important reflector is the ionosphere which can change the wave's polarization. Thus for signals received following reflection by the ionosphere (a skywave), a consistent polarization cannot be expected. For line-of-sight communications or ground wave propagation, horizontally or vertically polarized transmissions generally remain in about the same polarization state at the receiving location. Matching the receiving antenna's polarization to that of the transmitter can make a very substantial difference in received signal strength.
Polarization is predictable from an antenna's geometry, although in some cases it is not at all obvious (such as for the quad antenna). An antenna's linear polarization is generally along the direction (as viewed from the receiving location) of the antenna's currents when such a direction can be defined. For instance, a vertical whip antenna or Wi-Fi antenna vertically oriented will transmit and receive in the vertical polarization. Antennas with horizontal elements, such as most rooftop TV antennas in the United States, are horizontally polarized (broadcast TV in the U.S. usually uses horizontal polarization). Even when the antenna system has a vertical orientation, such as an array of horizontal dipole antennas, the polarization is in the horizontal direction corresponding to the current flow. The polarization of a commercial antenna is an essential specification.
Polarization is the sum of the E-plane orientations over time projected onto an imaginary plane perpendicular to the direction of motion of the radio wave. In the most general case, polarization is elliptical, meaning that the polarization of the radio waves varies over time. Two special cases are linear polarization (the ellipse collapses into a line) as discussed above, and circular polarization (in which the two axes of the ellipse are equal). In linear polarization the electric field of the radio wave oscillates back and forth along one direction; this can be affected by the mounting of the antenna but usually the desired direction is either horizontal or vertical polarization. In circular polarization, the electric field (and magnetic field) of the radio wave rotates at the radio frequency circularly around the axis of propagation. Circular or elliptically polarized radio waves are designated as right-handed or left-handed using the "thumb in the direction of the propagation" rule. For circular polarization, optical researchers use the opposite right hand rule from the one used by radio engineers.
It is best for the receiving antenna to match the polarization of the transmitted wave for optimum reception. Intermediate matchings will lose some signal strength, but not as much as a complete mismatch. A circularly polarized antenna can be used to equally well match vertical or horizontal linear polarizations. Transmission from a circularly polarized antenna received by a linearly polarized antenna (or vice versa) entails a 3 dB reduction in signal-to-noise ratio as the received power has thereby been cut in half.
Impedance matching
Maximum power transfer requires matching the impedance of an antenna system (as seen looking into the transmission line) to the complex conjugate of the impedance of the receiver or transmitter. In the case of a transmitter, however, the desired matching impedance might not correspond to the dynamic output impedance of the transmitter as analyzed as a source impedance but rather the design value (typically 50 ohms) required for efficient and safe operation of the transmitting circuitry. The intended impedance is normally resistive but a transmitter (and some receivers) may have additional adjustments to cancel a certain amount of reactance in order to "tweak" the match. When a transmission line is used in between the antenna and the transmitter (or receiver) one generally would like an antenna system whose impedance is resistive and near the characteristic impedance of that transmission line in order to minimize the standing wave ratio (SWR) and the increase in transmission line losses it entails, in addition to supplying a good match at the transmitter or receiver itself.
Antenna tuning generally refers to cancellation of any reactance seen at the antenna terminals, leaving only a resistive impedance which might or might not be exactly the desired impedance (that of the transmission line). Although an antenna may be designed to have a purely resistive feedpoint impedance (such as a dipole 97% of a half wavelength long) this might not be exactly true at the frequency that it is eventually used at. In some cases the physical length of the antenna can be "trimmed" to obtain a pure resistance. On the other hand, the addition of a series inductance or parallel capacitance can be used to cancel a residual capacitative or inductive reactance, respectively.
In some cases this is done in a more extreme manner, not simply to cancel a small amount of residual reactance, but to resonate an antenna whose resonance frequency is quite different from the intended frequency of operation. For instance, a "whip antenna" can be made significantly shorter than 1/4 wavelength long, for practical reasons, and then resonated using a so-called loading coil. This physically large inductor at the base of the antenna has an inductive reactance which is the opposite of the capacitative reactance that such a vertical antenna has at the desired operating frequency. The result is a pure resistance seen at feedpoint of the loading coil; that resistance is somewhat lower than would be desired to match commercial coax.
So an additional problem beyond canceling the unwanted reactance is of matching the remaining resistive impedance to the characteristic impedance of the transmission line. In principle this can be done with a transformer, however the turns ratio of a transformer is not adjustable. A general matching network with at least two adjustments can be made to correct both components of impedance. Matching networks using discrete inductors and capacitors will have losses associated with those components, and will have power restrictions when used for transmitting. Avoiding these difficulties, commercial antennas are generally designed with fixed matching elements or feeding strategies to get an approximate match to standard coax, such as 50 or 75 ohms. Antennas based on the dipole (rather than vertical antennas) may include a balun between the transmission line and antenna element, which may be integrated into any such matching network.
Another extreme case of impedance matching occurs when using a small loop antenna (usually, but not always, for receiving) at a relatively low frequency where it appears almost as a pure inductor. Resonating such an inductor with a capacitor at the frequency of operation not only cancels the reactance but greatly magnifies the very small radiation resistance of such a loop. This is implemented in most AM broadcast receivers, with a small ferrite loop antenna resonated by a capacitor which is varied along with the receiver tuning in order to maintain resonance over the AM broadcast band
Antenna types
Antennas can be classified in various ways. The list below groups together antennas under common operating principles, following the way antennas are classified in many engineering textbooks.
Isotropic: An isotropic antenna (isotropic radiator) is a hypothetical antenna that radiates equal signal power in all directions. It is a mathematical model that is used as the base of comparison to calculate the gain of real antennas. No real antenna can have an isotropic radiation pattern. However approximately isotropic antennas, constructed with multiple elements, are used in antenna testing.
The first four groups below are usually resonant antennas; when driven at their resonant frequency their elements act as resonators. Waves of current and voltage bounce back and forth between the ends, creating standing waves along the elements.
Dipole
The dipole is the prototypical antenna on which a large class of antennas are based. A basic dipole antenna consists of two conductors (usually metal rods or wires) arranged symmetrically, with one side of the balanced feedline from the transmitter or receiver attached to each.[18][21] The most common type, the half-wave dipole, consists of two resonant elements just under a quarter wavelength long. This antenna radiates maximally in directions perpendicular to the antenna's axis, giving it a small directive gain of 2.15 dBi. Although half-wave dipoles are used alone as omnidirectional antennas, they are also a building block of many other more complicated directional antennas.
- Yagi-Uda – One of the most common directional antennas at HF, VHF, and UHF frequencies. Consists of multiple half wave dipole elements in a line, with a single driven element and multiple parasitic elements which serve to create a uni-directional or beam antenna. These typically have gains between 10–20 dBi depending on the number of elements used, and are very narrowband (with a usable bandwidth of only a few percent) though there are derivative designs which relax this limitation. Used for rooftop television antennas, point-to-point communication links, and long distance shortwave communication using skywave ("skip") reflection from the ionosphere.
- Log-periodic dipole array – Often confused with the Yagi-Uda, this consists of many dipole elements along a boom with gradually increasing lengths, all connected to the transmission line with alternating polarity. It is a directional antenna with a wide bandwidth. This makes it ideal for use as a rooftop television antenna, although its gain is much less than a Yagi of comparable size.
- Turnstile – Two dipole antennas mounted at right angles, fed with a phase difference of 90°. This antenna is unusual in that it radiates in all directions (no nulls in the radiation pattern), with horizontal polarization in directions coplanar with the elements, circular polarization normal to that plane, and elliptical polarization in other directions. Used for receiving signals from satellites, as circular polarization is transmitted by many satellites.
- Corner reflector – A directive antenna with moderate gain of about 8 dBi often used at UHF frequencies. Consists of a dipole mounted in front of two reflective metal screens joined at an angle, usually 90°. Used as a rooftop UHF television antenna and for point-to-point data links.
- Patch (microstrip) – A type of antenna with elements consisting of metal sheets mounted over a ground plane. Similar to dipole with gain of 6–9 dBi. Integrated into surfaces such as aircraft bodies. Their easy fabrication using PCB techniques have made them popular in modern wireless devices. Often combined into arrays.
Monopole
A monopole antenna is a half-dipole, with some provision to compensate for the missing half. The monopole consist of a single conductor such as a metal rod, mounted over the ground or an artificial conducting surface (a so-called ground plane).[18][22] One side of the feedline from the receiver or transmitter is connected to the conductor, and the other side to ground or the artificial ground plane. The monopole is best understood as a dipole antenna in which one conductor is omitted; the radiation is generated as if the second arm of the dipole were present due to the effective image current seen as a reflection of the monopole from the ground. Since all of the equivalent dipole's radiation is concentrated in a half-space, the antenna has twice (3 dB increase of) the gain of a similar dipole, not considering losses in the ground plane.
The most common form is the quarter-wave monopole which is one-quarter of a wavelength long and has a gain of 5.12 dBi when mounted over a ground plane. Monopoles have an omnidirectional radiation pattern, so they are used for broad coverage of an area, and have vertical polarization. The ground waves used for broadcasting at low frequencies must be vertically polarized, so large vertical monopole antennas are used for broadcasting in the MF, LF, and VLF bands. Small monopoles are used as nondirectional antennas on portable radios in the HF, VHF, and UHF bands.
- Whip – Type of antenna used on mobile and portable radios in the VHF and UHF bands such as boom boxes, consists of a flexible rod, often made of telescoping segments.
- Rubber Ducky – Most common antenna used on portable two way radios and cordless phones due to its compactness, consists of an electrically short wire helix. The helix adds inductance to cancel the capacitive reactance of the short radiator, making it resonant. Very low gain.
- Ground plane – a whip antenna with several rods extending horizontally from base of whip attached to the ground side of the feedline. Since whips are mounted above ground, the horizontal rods form an artificial ground plane under the antenna to increase its gain. Used as base station antennas for land mobile radio systems such as police, ambulance and taxi dispatchers.
- Mast radiator – A radio tower in which the tower structure itself serves as the antenna. Common form of transmitting antenna for AM radio stations and other MF and LF transmitters. At its base the tower is usually, but not necessarily, mounted on a ceramic insulator to isolate it from the ground.
- T and inverted L – Consist of a long horizontal wire suspended between two towers with insulators, with a vertical wire hanging down from it, attached to a feedline to the receiver or transmitter. Used on LF and VLF bands. The vertical wire serves as the radiator. Since at these frequencies the vertical wire is electrically short, much shorter than a quarter wavelength, the horizontal wire(s) serve as a capacitive "hat" to increase the current in the vertical radiator, increasing the gain. Very narrow bandwidth, requires loading coil to tune out any remaining capacitive reactance. Requires low resistance ground (electricity).
- Inverted F – Combines the advantages of the compactness of inverted-L antenna, and the good matching of the F-type antenna. The antenna is grounded at the base and fed at some intermediate point. The position of the feed point determines the antenna impedance. Thus, matching can be achieved without the need for an extraneous matching network.
- Umbrella – Very large wire transmitting antennas used on VLF bands. Consists of a central mast radiator tower attached at the top to multiple wires extending out radially from the mast to ground, like a tent or umbrella, insulated at the ends. Extremely narrow bandwidth, requires large loading coil and low resistance counterpoise ground. Used for long range military communications.
Array
Array antennas consist of multiple antennas working as a single antenna. Typically they consist of arrays of identical driven elements, usually dipoles fed in phase, giving increased gain over that of a single dipole.[18][23][24]
- Collinear - Consist of a number of dipoles in a vertical line. It is a high gain omnidirectional antenna, meaning more of the power is radiated in horizontal directions and less into the sky or ground and wasted. Gain of 8 to 10 dBi. Used as base station antennas for land mobile radio systems such as police, fire, ambulance, and taxi dispatchers, and sector antennas for cellular base stations.
- Reflective array - multiple dipoles in a two-dimensional array mounted in front of a flat reflecting screen. Used for radar and UHF television transmitting and receiving antennas.
- Phased array - A high gain antenna used at UHF and microwave frequencies which is electronically steerable. It consists of multiple dipoles in a two-dimensional array, each fed through an electronic phase shifter, with the phase shifters controlled by a computer control system. The beam can be instantly pointed in any direction over a wide angle in front of the antenna. Used for military radar and jamming systems.
- Curtain array - Large directional wire transmitting antenna used at HF by shortwave broadcasting stations. It consists of a vertical rectangular array of wire dipoles suspended in front of a flat reflector screen consisting of a vertical "curtain" of parallel wires, all supported between two metal towers. It radiates a horizontal beam of radio waves into the sky above the horizon, which is reflected by the ionosphere to Earth beyond the horizon
- Batwing or superturnstile - A specialized antenna used in television broadcasting consisting of perpendicular pairs of dipoles with radiators resembling bat wings. Multiple batwing antennas are stacked vertically on a mast to make VHF television broadcast antennas. Omnidirectional radiation pattern with high gain in horizontal directions. The batwing shape gives them wide bandwidth.
- Microstrip - an array of patch antennas on a substrate fed by microstrip feedlines. Microwave antenna that can achieve large gains in compact space. Ease of fabrication by PCB techniques have made them popular in modern wireless devices. Beamwidth and polarization can be actively reconfigurable.
Loop
Loop antennas consist of a loop (or coil) of wire. There are essentially two broad categories of loop antennas: big loops and small loops. Loops with circumference of a wavelength (or integer multiple of the wavelength) are naturally resonant and act somewhat similarly to the half-wave dipole, and when it is necessary to distinguish them from small loops, they are called “full-wave” loops. (The popular “quad” antenna design is necessarily a full-wave loop, so no other distinction is needed.)
If the loop is small in comparison to the wavelength it must be modified in some way to make it resonant if that is necessary. Small loops are called “magnetic loops” or “tuned loops”. They function quite differently from full-wave loops. This antenna interacts directly with the magnetic field of the radio wave, making it relatively insensitive to nearby electrical noise. However it has a very small radiation resistance, typically much smaller than the loss resistance, making it inefficient and thus undesirable for transmitting. They are used as receiving antennas at low frequencies, and also as direction finding antennas.
- Ferrite (loopstick) – These are used as the receiving antenna in most consumer AM radios operating in the medium wave broadcast band (and lower frequencies), a notable exception being car radios. Wire is coiled around a ferrite core which greatly increases the coil's inductance. Radiation pattern is maximum at directions perpendicular to the ferrite rod. The null direction of ferrite core antennas are bi-directional and sharper than the maximal directionality. This often makes the null direction more useful than the maximal directionality because the null direction can be used to reject unwanted signals from an interfering station or noise source.
- Quad – Quad antennas are made of multiple full-wave loops, lined up in a row along their axes; they resemble the frame of a box kite. One loop in the quad is connected to the feedline and functions as the diver for the antenna and the signal radiator. The other loops are “helpers”; they are not connected to the feed, but are spaced and tuned so that they intercept and reflect the rearward signal from the driven loop back forward, and focus the forward-traveling signal into a narrower beam – like mirrors and lenses in a flashlight. They are called “reflectors” or “directors”, depending on function, or in general parasitic elements since they borrow energy from the field created by the driven element. Quad antennas are the exact analogue, for loops, to a Yagi-Uda antenna made out of dipoles; in fact, a “Yagi” can be built using a mixture of loops and dipoles. Similar to Yagis, quads are used as a directional antennas on the HF bands for shortwave communication, and are sometimes preferred for longer wavelengths because (if square) they are half as wide as a Yagi.
Aperture
Aperture antennas are the main type of directional antennas used at microwave frequencies and above. They consist of a small dipole or loop feed antenna inside a three-dimensional guiding structure large compared to a wavelength, with an aperture to emit the radio waves. Since the antenna structure itself is nonresonant they can be used over a wide frequency range by replacing or tuning the feed antenna.
- Parabolic - The most widely used high gain antenna at microwave frequencies and above. Consists of a dish-shaped metal parabolic reflector with a feed antenna at the focus. It can have some of the highest gains of any antenna type, up to 60 dBi, but the dish must be large compared to a wavelength. Used for radar antennas, point-to-point data links, satellite communication, and radio telescopes
- Horn - Simple antenna with moderate gains of 15 to 25 dBi consists of a flaring metal horn attached to a waveguide. Used for applications such as radar guns, radiometers and as feed antennas for parabolic dishes.
- Slot - Consist of a waveguide with one or more slots cut in it to emit the microwaves. Linear slot antennas emit narrow fan-shaped beams. Used as UHF broadcast antennas and marine radar antennas.
- Dielectric resonator - consists of small ball or puck-shaped piece of dielectric material excited by aperture in waveguide Used at millimeter wave frequencies
Traveling wave
Unlike the above antennas, traveling wave antennas are nonresonant so they have inherently broad bandwidth. They are typically wire antennas multiple wavelengths long, through which the voltage and current waves travel in one direction, instead of bouncing back and forth to form standing waves as in resonant antennas. They have linear polarization (except for the helical antenna). Unidirectional traveling wave antennas are terminated by a resistor at one end equal to the antenna's characteristic resistance, to absorb the waves from one direction. This makes them inefficient as transmitting antennas.
- Random wire - This describes the typical antenna used to receive shortwave radio, consisting of a random length of wire either strung outdoors between supports or indoors in a zigzag pattern along walls, connected to the receiver at one end. Can have complex radiation patterns with several lobes at angles to the wire.
- Beverage - Simplest unidirectional traveling wave antenna. Consists of a straight wire one to several wavelengths long, suspended near the ground, connected to the receiver at one end and terminated by a resistor equal to its characteristic impedance, 400 to 800Ω at the other end. Its radiation pattern has a main lobe at a shallow angle in the sky off the terminated end. It is used for reception of skywaves reflected off the ionosphere in long distance "skip" shortwave communication.
- Rhombic - Consists of four equal wire sections shaped like a rhombus. It is fed by a balanced feedline at one of the acute corners, and the two sides are connected to a resistor equal to the characteristic resistance of the antenna at the other. It has a main lobe in a horizontal direction off the terminated end of the rhombus. Used for skywave communication on shortwave bands.
- Helical (axial mode) - Consists of a wire in the shape of a helix mounted above a reflecting screen. It radiates circularly polarized waves in a beam off the end, with a typical gain of 15 dBi. It is used at VHF and UHF frequencies. Often used for satellite communication, which uses circular polarization because it is insensitive to the relative rotation on the beam axis.
- Leaky wave - Microwave antennas consisting of a waveguide or coaxial cable with a slot or apertures cut in it so it radiates continuously along its length.
Effect of ground
Ground reflections is one of the common types of multipath.
The radiation pattern and even the driving point impedance of an antenna can be influenced by the dielectric constant and especially conductivity of nearby objects. For a terrestrial antenna, the ground is usually one such object of importance. The antenna's height above the ground, as well as the electrical properties (permittivity and conductivity) of the ground, can then be important. Also, in the particular case of a monopole antenna, the ground (or an artificial ground plane) serves as the return connection for the antenna current thus having an additional effect, particularly on the impedance seen by the feed line.
When an electromagnetic wave strikes a plane surface such as the ground, part of the wave is transmitted into the ground and part of it is reflected, according to the Fresnel coefficients. If the ground is a very good conductor then almost all of the wave is reflected (180° out of phase), whereas a ground modeled as a (lossy) dielectric can absorb a large amount of the wave's power. The power remaining in the reflected wave, and the phase shift upon reflection, strongly depend on the wave's angle of incidence and polarization. The dielectric constant and conductivity (or simply the complex dielectric constant) is dependent on the soil type and is a function of frequency.
For very low frequencies to high frequencies (<30 MHz), the ground behaves as a lossy dielectric,[32] thus the ground is characterized both by a conductivity[33] and permittivity (dielectric constant) which can be measured for a given soil (but is influenced by fluctuating moisture levels) or can be estimated from certain maps. At lower frequencies the ground acts mainly as a good conductor, which AM middle wave broadcast (.5 - 1.6 MHz) antennas depend on.
At frequencies between 3 and 30 MHz, a large portion of the energy from a horizontally polarized antenna reflects off the ground, with almost total reflection at the grazing angles important for ground wave propagation. That reflected wave, with its phase reversed, can either cancel or reinforce the direct wave, depending on the antenna height in wavelengths and elevation angle (for a sky wave).
On the other hand, vertically polarized radiation is not well reflected by the ground except at grazing incidence or over very highly conducting surfaces such as sea water.[34] However the grazing angle reflection important for ground wave propagation, using vertical polarization, is in phase with the direct wave, providing a boost of up to 6 db, as is detailed below.
At VHF and above (>30 MHz) the ground becomes a poorer reflector. However it remains a good reflector especially for horizontal polarization and grazing angles of incidence. That is important as these higher frequencies usually depend on horizontal line-of-sight propagation (except for satellite communications), the ground then behaving almost as a mirror.
The net quality of a ground reflection depends on the topography of the surface. When the irregularities of the surface are much smaller than the wavelength, the dominant regime is that of specular reflection, and the receiver sees both the real antenna and an image of the antenna under the ground due to reflection. But if the ground has irregularities not small compared to the wavelength, reflections will not be coherent but shifted by random phases. With shorter wavelengths (higher frequencies), this is generally the case.
Whenever both the receiving or transmitting antenna are placed at significant heights above the ground (relative to the wavelength), waves specularly reflected by the ground will travel a longer distance than direct waves, inducing a phase shift which can sometimes be significant. When a sky wave is launched by such an antenna, that phase shift is always significant unless the antenna is very close to the ground (compared to the wavelength).
The phase of reflection of electromagnetic waves depends on the polarization of the incident wave. Given the larger refractive index of the ground (typically n=2) compared to air (n=1), the phase of horizontally polarized radiation is reversed upon reflection (a phase shift of radians or 180°). On the other hand, the vertical component of the wave's electric field is reflected at grazing angles of incidence approximately in phase. These phase shifts apply as well to a ground modelled as a good electrical conductor.
This means that a receiving antenna "sees" an image of the antenna but with reversed currents. That current is in the same absolute direction as the actual antenna if the antenna is vertically oriented (and thus vertically polarized) but opposite the actual antenna if the antenna current is horizontal.
The actual antenna which is transmitting the original wave then also may receive a strong signal from its own image from the ground. This will induce an additional current in the antenna element, changing the current at the feedpoint for a given feedpoint voltage. Thus the antenna's impedance, given by the ratio of feedpoint voltage to current, is altered due to the antenna's proximity to the ground. This can be quite a significant effect when the antenna is within a wavelength or two of the ground. But as the antenna height is increased, the reduced power of the reflected wave (due to the inverse square law) allows the antenna to approach its asymptotic feedpoint impedance given by theory. At lower heights, the effect on the antenna's impedance is very sensitive to the exact distance from the ground, as this affects the phase of the reflected wave relative to the currents in the antenna. Changing the antenna's height by a quarter wavelength, then changes the phase of the reflection by 180°, with a completely different effect on the antenna's impedance.
The ground reflection has an important effect on the net far field radiation pattern in the vertical plane, that is, as a function of elevation angle, which is thus different between a vertically and horizontally polarized antenna. Consider an antenna at a height h above the ground, transmitting a wave considered at the elevation angle θ. For a vertically polarized transmission the magnitude of the electric field of the electromagnetic wave produced by the direct ray plus the reflected ray is:
Thus the power received can be as high as 4 times that due to the direct wave alone (such as when θ=0), following the square of the cosine. The sign inversion for the reflection of horizontally polarized emission instead results in:
where:
- is the electrical field that would be received by the direct wave if there were no ground.
- θ is the elevation angle of the wave being considered.
- is the wavelength.
- is the height of the antenna (half the distance between the antenna and its image).
For horizontal propagation between transmitting and receiving antennas situated near the ground reasonably far from each other, the distances traveled by the direct and reflected rays are nearly the same. There is almost no relative phase shift. If the emission is polarized vertically, the two fields (direct and reflected) add and there is maximum of received signal. If the signal is polarized horizontally, the two signals subtract and the received signal is largely cancelled. The vertical plane radiation patterns are shown in the image at right. With vertical polarization there is always a maximum for θ=0, horizontal propagation (left pattern). For horizontal polarization, there is cancellation at that angle. Note that the above formulae and these plots assume the ground as a perfect conductor. These plots of the radiation pattern correspond to a distance between the antenna and its image of 2.5λ. As the antenna height is increased, the number of lobes increases as well.
The difference in the above factors for the case of θ=0 is the reason that most broadcasting (transmissions intended for the public) uses vertical polarization. For receivers near the ground, horizontally polarized transmissions suffer cancellation. For best reception the receiving antennas for these signals are likewise vertically polarized. In some applications where the receiving antenna must work in any position, as in mobile phones, the base station antennas use mixed polarization, such as linear polarization at an angle (with both vertical and horizontal components) or circular polarization.
On the other hand, analog television transmissions are usually horizontally polarized, because in urban areas buildings can reflect the electromagnetic waves and create ghost images due to multipath propagation. Using horizontal polarization, ghosting is reduced because the amount of reflection in the horizontal polarization off the side of a building is generally less than in the vertical direction. Vertically polarized analog television have been used in some rural areas. In digital terrestrial television such reflections are less problematic, due to robustness of binary transmissions and error correction.
Mutual impedance and interaction between antennas
Current circulating in one antenna generally induces a voltage across the feedpoint of nearby antennas or antenna elements. The mathematics presented below are useful in analyzing the electrical behaviour of antenna arrays, where the properties of the individual array elements (such as half wave dipoles) are already known. If those elements were widely separated and driven in a certain amplitude and phase, then each would act independently as that element is known to. However, because of the mutual interaction between their electric and magnetic fields due to proximity, the currents in each element are not simply a function of the applied voltage (according to its driving point impedance), but depend on the currents in the other nearby elements. This now is a near field phenomenon which could not be properly accounted for using the Friis transmission formula for instance. This near field effect creates a different set of currents at the antenna terminals resulting in distortions in the far field radiation patterns; however, the distortions may be removed using a simple set of network equations.
The elements' feedpoint currents and voltages can be related to each other using the concept of mutual impedance between every pair of antennas just as the mutual impedance describes the voltage induced in one inductor by a current through a nearby coil coupled to it through a mutual inductance M. The mutual impedance between two antennas is defined as:
where is the current flowing in antenna i and is the voltage induced at the open-circuited feedpoint of antenna j due to when all other currents ik are zero. The mutual impendances can be viewed as the elements of a symmetric square impedance matrix Z. Note that the diagonal elements, , are simply the driving point impedances of each element.
Using this definition, the voltages present at the feedpoints of a set of coupled antennas can be expressed as the multiplication of the impedance matrix times the vector of currents. Written out as discrete equations, that means:
where:
- is the voltage at the terminals of antenna
- is the current flowing between the terminals of antenna
- is the driving point impedance of antenna
- is the mutual impedance between antennas and .
As is the case for mutual inductances,
This is a consequence of Lorentz reciprocity. For an antenna element not connected to anything (open circuited) one can write . But for an element which is short circuited, a current is generated across that short but no voltage is allowed, so the corresponding . This is the case, for instance, with the so-called parasitic elements of a Yagi-Uda antenna where the solid rod can be viewed as a dipole antenna shorted across its feedpoint. Parasitic elements are unpowered elements that absorb and reradiate RF energy according to the induced current calculated using such a system of equations.
With a particular geometry, it is possible for the mutual impedance between nearby antennas to be zero. This is the case, for instance, between the crossed dipoles used in the turnstile antenna.
Smart antenna
Smart antennas (also known as adaptive array antennas, digital antenna arrays, multiple antennas and, recently, MIMO) are antenna arrays with smart signal processing algorithms used to identify spatial signal signatures such as the direction of arrival (DOA) of the signal, and use them to calculate beamforming vectors which are used to track and locate the antenna beam on the mobile/target. Smart antennas should not be confused with reconfigurable antennas, which have similar capabilities but are single element antennas and not antenna arrays.
Smart antenna techniques are used notably in acoustic signal processing, track and scan radar, radio astronomy and radio telescopes, and mostly in cellular systems like W-CDMA, UMTS, and LTE.
Smart antennas have many functions: DOA estimation, beamforming, interference nulling, and constant modulus preservation..
Direction of arrival (DOA) estimation
The smart antenna system estimates the direction of arrival of the signal, using techniques such as MUSIC (MUltiple SIgnal Classification), estimation of signal parameters via rotational invariance techniques (ESPRIT) algorithms, Matrix Pencil method or one of their derivatives. They involve finding a spatial spectrum of the antenna/sensor array, and calculating the DOA from the peaks of this spectrum. These calculations are computationally intensive.
Matrix Pencil is very efficient in case of real time systems, and under the correlated sources.
Beamforming
Beamforming is the method used to create the radiation pattern of the antenna array by adding constructively the phases of the signals in the direction of the targets/mobiles desired, and nulling the pattern of the targets/mobiles that are undesired/interfering targets. This can be done with a simple Finite Impulse Response (FIR) tapped delay line filter. The weights of the FIR filter may also be changed adaptively, and used to provide optimal beamforming, in the sense that it reduces the Minimum Mean Square Error between the desired and actual beampattern formed. Typical algorithms are the steepest descent, and Least Mean Squares algorithms. In digital antenna arrays with multi channels use the digital beamforming, usually by DFT or FFT.
Types of smart antennas
Two of the main types of smart antennas include switched beam smart antennas and adaptive array smart antennas. Switched beam systems have several available fixed beam patterns. A decision is made as to which beam to access, at any given point in time, based upon the requirements of the system. Adaptive arrays allow the antenna to steer the beam to any direction of interest while simultaneously nulling interfering signals. Beamdirection can be estimated using the so-called direction-of-arrival (DOA) estimation methods.
In 2008, the United States NTIA began a major effort to assist consumers in the purchase of digital television converter boxes.[1] Through this effort, many people have been exposed to the concept of smart antennas for the first time. In the context of consumer electronics, a "smart antenna" is one that conforms to the EIA/CEA-909 Standard Interface.
In 2017, the Israeli Aerospace Industries have unvailed an adaptive array antenna called ADA, and stated that it is already operational and shall be fitted onto "major platforms" used by the IDF.
Limited choice of EIA/CEA-909A smart antennas in the marketplace
Prior to the final transition to ATSC digital television in the United States on June 11, 2009, two smart antenna models were brought to market:
- RCA ANT2000 – no longer available from retailers
- DTA-5000 – manufactured by Funai Electric, marketed under the "DX Antenna" brand name, sometimes associated with the Sylvania brand name; no longer available from retailers
And two models are causing consumer confusion:
- Although the Apex SM550 is capable of connecting to a CEA-909 port for the purpose of drawing electrical power, it is not a true smart antenna.
- The unfortunately-named Channel Master 3000A and CM3000HD SMARTenna series are otherwise-conventional amplified omnidirectional antennas, not steerable smart antennas.
- ADA - An adaptive antenna produced by MLM factory of the Israel Aerospace Industries
Extension of smart antennas
Smart antenna systems are also a defining characteristic of MIMO systems , such as the IEEE 802.11n standard. Conventionally, a smart antenna is a unit of a wireless communication system and performs spatial signal processing with multiple antennas. Multiple antennas can be used at either the transmitter or receiver. Recently, the technology has been extended to use the multiple antennas at both the transmitter and receiver; such a system is called a multiple-input multiple-output (MIMO) system [8] . As extended Smart Antenna technology, MIMO supports spatial information processing, in the sense that conventional research on Smart Antennas has focused on how to provide a digital beamforming advantage by the use of spatial signal processing in wireless channels. Spatial information processing includes spatial information coding such as Spatial multiplexing and Diversity Coding, as well as beamforming.
XXX . XXX 4%zero Antenna tuner
An antenna tuner, a matchbox, transmatch, antenna tuning unit (ATU), antenna coupler, or feedline coupler is a device connected between a radio transmitter or receiver and its antenna to improve power transfer between them by matching the impedance of the radio to the antenna's feedline. Antenna tuners are particularly important for use with transmitters. Transmitters feed power into a resistive load, very often 50 ohms, for which the transmitter is optimally designed for power output, efficiency, and low distortion. If the load seen by the transmitter departs from this design value due to improper tuning of the antenna/feedline combination the power output will change, distortion may occur and the transmitter may overheat.
ATUs are a standard part of almost all radio transmitters; they may be a circuit included inside the transmitter itself or a separate piece of equipment connected between the transmitter and the antenna. In transmitters in which the antenna is mounted separate from the transmitter and connected to it by a transmission line (feedline), there may be a second ATU (or matching network) at the antenna to match the impedance of the antenna to the transmission line.
In low power transmitters with attached antennas, such as cell phones and walkie-talkies, the ATU is fixed to work with the antenna. In high power transmitters like radio stations, the ATU is adjustable to accommodate changes in the antenna or transmitter, and adjusting the ATU to match the transmitter to the antenna is an important procedure done after any changes to these components have been made. The effect of this adjustment is observed with an instrument called an SWR meter.
In some radio receivers applications, ATUs are not as important because in the low frequency part of the radio spectrum noise in the signal to noise ratio (SNR) is dominated by atmospheric noise. It may not matter if the impedance of the antenna and receiver are mismatched so some of the incoming power from the antenna is reflected and does not reach the receiver, because the signal can be amplified to make up for it. However in higher frequency receivers the noise in the SNR is dominated by noise generated in the receiver's front end, so it is important that the receiving antenna is impedance-matched to the receiver to give maximum signal amplitude in the front end stages, to overcome noise.
Overview
An antenna's impedance is different at different frequencies. An antenna tuner matches a radio with a fixed impedance (typically 50 Ohms for modern transceivers) to the combination of the feedline and the antenna; useful when the impedance seen at the input end of the feedline is unknown, complex, or otherwise different from the transceiver. Coupling through an ATU allows the use of one antenna on a broad range of frequencies.
Despite its name, an antenna ‘tuner ’ does not directly tune the antenna. It matches the transmitter to the complex impedance reflected back to the input end of the feedline. If both tuner and transmission line were lossless, tuning at the transmitter end would indeed produce a perfect match at every point in the transmitter-feedline-antenna system. However, in practical systems feedline losses limit the ability of the antenna ‘tuner’ to match the antenna or change its resonant frequency. If the loss of power is low in the line carrying the transmitter's signal into the antenna, a tuner at the transmitter end can produce a worthwhile degree of matching and tuning for the antenna and feedline network as a whole.[3][4] With lossy feedlines (such as commonly used 50 Ohm coaxial cable) maximum power transfer only occurs if matching is done at both ends of the line.
If there is still a high SWR in the feedline beyond the ATU, any loss in the feedline is multiplied several times by the transmitted waves reflecting back and forth between the tuner and the antenna, heating the wire instead of sending out a signal. Even with a matching unit at both ends of the feedline – the near ATU matching the transmitter to the feedline and the remote ATU matching the feedline to the antenna – losses in the circuitry of the two ATUs will reduce power delivered to the antenna. Therefore, operating an antenna far from its design frequency and compensating with a transmatch between the transmitter and the feedline is not as efficient as using a resonant antenna with a matched-impedance feedline, nor as efficient as a matched feedline from the transmitter to a remote antenna tuner attached directly to the antenna.
Broad band matching methods
Transformers, autotransformers, and baluns are sometimes incorporated into the design of narrow band antenna tuners and antenna cabling connections. They will all usually have little effect on the resonant frequency of either the antenna or the narrow band transmitter circuits, but can widen the range of impedances that the antenna tuner can match, and/or convert between balanced and unbalanced cabling where needed.
Ferrite transformers
Solid-state power amplifiers operating from 1–30 MHz typically use one or more wideband transformers wound on ferrite cores. MOSFETs and bipolar junction transistors are designed to operate into a low impedance, so the transformer primary typically has a single turn, while the 50 Ohm secondary will have 2 to 4 turns. This feedline system design has the advantage of reducing the retuning required when the operating frequency is changed. A similar design can match an antenna to a transmission line; For example, many TV antennas have a 300 Ohm impedance and feed the signal to the TV via a 75 Ohm coaxial line. A small ferrite core transformer makes the broad band impedance transformation. This transformer does not need, nor is it capable of adjustment. For receive-only use in a TV the small SWR variation with frequency is not a major problem.
It should be added that many ferrite based transformers perform a balanced to unbalanced transformation along with the impedance change. When the balanced to unbalanced function is present these transformers are called a balun (otherwise an unun). The most common baluns have either a 1:1 or a 1:4 impedance transformation.
Autotransformers
There are several designs for impedance matching using an autotransformer, which is a single-wire transformer with different connection points or taps spaced along the windings. They are distinguished mainly by their impedance transform ratio (1:1, 1:4, 1:9, etc., the square of the winding ratio), and whether the input and output sides share a common ground, or are matched from a cable that is grounded on one side (unbalanced) to an ungrounded (usually balanced) cable. When autotransformers connect balanced and unbalanced lines they are called baluns, just as two-winding transformers. When two differently-grounded cables or circuits must be connected but the grounds kept independent, a full, two-winding transformer with the desired ratio is used instead.
The circuit pictured at the right has three identical windings wrapped in the same direction around either an "air" core (for very high frequencies) or ferrite core (for middle, or low frequencies). The three equal windings shown are wired for a common ground shared by two unbalanced lines (so this design is called an unun), and can be used as 1:1, 1:4, or 1:9 impedance match, depending on the tap chosen. (The same windings could be connected differently to make a balun instead.)
For example, if the right-hand side is connected to a resistive load of 10 Ohms, the user can attach a source at any of the three ungrounded terminals on the left side of the autotransformer to get a different impedance. Notice that on the left side, the line with more windings measures greater impedance for the same 10 Ohm load on the right.
Narrow band design
The "narrow-band" methods described below cover a very much smaller span of frequencies, by comparison with the broadband methods described above.
Antenna matching methods that use transformers tend to cover a wide range of frequencies. A single, typical, commercially available balun can cover frequencies from 3.5–30.0 MHz, or nearly the entire shortwave radio band. Matching to an antenna using a cut segment of transmission line (described below) is perhaps the most efficient of all matching schemes in terms of electrical power, but typically can only cover a range about 3.5–3.7 MHz wide – a very small range indeed, compared to a broadband balun. Antenna coupling or feedline matching circuits are also narrowband for any single setting, but can be re-tuned more conveniently. However they are perhaps the least efficient in terms of power-loss (aside from having no impedance matching at all!).
Transmission line antenna tuning methods
The insertion of a special section of transmission line, whose characteristic impedance differs from that of the main line, can be used to match the main line to the antenna. An inserted line with the proper impedance and connected at the proper location can perform complicated matching effects with very high efficiency, but spans a very limited frequency range.
The simplest example this method is the quarter-wave impedance transformer formed by a section of mismatched transmission line. If a quarter-wavelength of 75 Ohm coaxial cable is linked to a 50 Ohm load, the SWR in the 75 Ohm quarter wavelength of line can be calculated as 75Ω / 50Ω = 1.5; the quarter-wavelength of line transforms the mismatched impedance to 112.5 Ohms (75 Ohms × 1.5 = 112.5 Ohms). Thus this inserted section matches a 112 Ohm antenna to a 50 Ohm main line.
The 1⁄6 wavelength coaxial transformer is a useful way to match 50 to 75 Ohms using the same general method.[6] The theoretical basis is discussion by the inventor, and wider application of the method is found here:
A second common method is the use of a stub: A shorted, or open section of line is connected in parallel with the main line. With coax this is done using a ‘T’-connector. The length of the stub and its location can be chosen so as to produce a matched line below the stub, regardless of the complex impedance or SWR of the antenna itself. The J-pole antenna is an example of an antenna with a built-in stub match.
Basic lumped circuit matching using the L network
The basic circuit required when lumped capacitances and inductors are used is shown below. This circuit is important in that many automatic antenna tuners use it, and also because more complicated circuits can be analyzed as groups of L-networks.
This is called an “L” network not because it contains an inductor, (in fact some L-networks consist of two capacitors), but because the two components are at right angles to each other, having the shape of a rotated and sometimes reversed English letter ‘L’. The ‘T’ (“Tee”) network and the π (“Pi”) network also have a shape similar to the English and Greek letters they are named after.
This basic network is able to act as an impedance transformer. If the output has an impedance consisting of resistance Rload and reactance j Xload, while the input is to be attached to a source which has an impedance of Rsource resistance and j Xsource reactance, then
and
- .
In this example circuit, XL and XC can be swapped. All the ATU circuits below create this network, which exists between systems with different impedances.
For instance, if the source has a resistive impedance of 50 Ω and the load has a resistive impedance of 1000 Ω :
If the frequency is 28 MHz,
As,
then,
So,
While as,
then,
Theory and practice
A parallel network, consisting of a resistive element (1000 Ω) and a reactive element (−j 229.415 Ω), will have the same impedance and power factor as a series network consisting of resistive (50 Ω) and reactive elements (−j 217.94 Ω).
By adding another element in series (which has a reactive impedance of +j 217.94 Ω), the impedance is 50 Ω (resistive).
Types of L networks and their use
The L-network can have eight different configurations, six of which are shown here. The two missing configurations are the same as the bottom row, but with the parallel element (wires vertical) on the right side of the series element (wires horizontal), instead of on the left, as shown.
In discussion of the diagrams that follows the in connector comes from the transmitter or "source"; the out connector goes to the antenna or "load". The general rule (with some exceptions, described below) is that the series element of an L-network goes on the side with the lowest impedance.[9]
So for example, the three circuits in the left column and the two in the bottom row have the series (horizontal) element on the out side are generally used for stepping up from a low-impedance input (transmitter) to a high-impedance output (antenna), similar to the example analyzed in the section above. The top two circuits in the right column, with the series (horizontal) element on the in side, are generally useful for stepping down from a higher input to a lower output impedance.
The general rule only applies to loads that are mainly resistive, with very little reactance. In cases where the load is highly reactive – such as an antenna fed with a signals whose frequency is far away from any resonance – the opposite configuration may be required. If far from resonance, the bottom two step down (high-in to low-out) circuits would instead be used to connect for a step up (low-in to high-out that is mostly reactance).[10]
The low- and high-pass versions of the four circuits shown in the top two rows use only one inductor and one capacitor. Normally, the low-pass would be preferred with a transmitter, in order to attenuate harmonics, but the high-pass configuration may be chosen if the components are more conveniently obtained, or if the radio already contains an internal low-pass filter, or if attenuation of low frequencies is desirable – for example when a local AM station broadcasting on a medium frequency may be overloading a high frequency receiver.
The Low R, high C circuit is shown feeding a short vertical antenna, such as would be the case for a compact, mobile antenna or otherwise on frequencies below an antenna's lowest natural resonant frequency. Here the inherent capacitance of a short, random wire antenna is so high that the L-network is best realized with two inductors, instead of aggravating the problem by using a capacitor.
The Low R, high L circuit is shown feeding a small loop antenna. Below resonance this type of antenna has so much inductance, that more inductance from adding a coil would make the reactance even worse. Therefore, the L-network is composed of two capacitors.
An L-network is the simplest circuit that will achieve the desired transformation; for any one given antenna and frequency, once a circuit is selected from the eight possible configurations (of which six are shown above) only one set of component values will match the in impedance to the out impedance.
More complicated ATU designs
In contrast to two-element L-networks, the circuits described below all have three or more components, and hence have many more choices for inductance and capacitance that will produce an impedance match. The radio operator must experiment, test, and use judgement to choose among the many adjustments that produce the same impedance match.
Unbalanced Line Tuners
High-pass T network
This configuration, although capable of matching a large impedance range, is a high-pass filter and will not attenuate spurious radiation above the cutoff frequency as much as the other types. Due to its low losses and simplicity, many home built and commercial manually tuned ATUs use this circuit.
Theory and practice
If a source impedance of 200 Ω and a resistive load of 1000 Ω are connected (via a capacitor with an impedance of −j 200 Ω) to the inductor of the transmatch, vector mathematics can transform this into a parallel network consisting of a resistance of 1040 Ω and a capacitor with an admittance of 1.9231×10−4 siemens (XC = 5200 Ω).
A resistive load (RL) of 1000 Ω is in series with XC −j 200 Ω.
The phase angle is
- Y = 1⁄Z = 9.8058×10−4 S
To convert to a parallel network
If the reactive component is ignored, a 1040 Ω to 200 Ω transformation is needed (according to the equations above, an inductor of +j 507.32 Ω). If the effect of the capacitor (from the parallel network) is taken into account, an inductor of +j 462.23 Ω is needed. The system can then be mathematically transformed into a series network of 199.9 Ω resistive and +j 409.82 Ω reactive.
A capacitor (−j 409.82) is needed to complete the network. The steps are shown here. Hover over each circuit for captions.
Low-pass π network
A π (pi) network can also be used. This ATU has very good attenuation of harmonics, but for multiband tuners the standard π circuit is not popular, since the variable capacitors are inconveniently large for the lower Amateur bands.
A modified version of the π-network is more practical as it uses a fixed input capacitor which can be several thousand picofarads while allowing the two variable capacitors to be smaller. A band switch selects the input capacitor and inductor. This circuit was used in tuners covering 1.8 to 30 MHz made by the R. L. Drake Company.
SPC tuner
The Series Parallel Capacitor or SPC tuner can serve both as an antenna coupler and as a preselector.
A simplified description of the SPC follows: In the diagram above, the upper capacitor on the right matches impedance to the antenna, and the single capacitor on the left matches impedance to the transmitter. The coil and the lower-right capacitor form a tank circuit that drains to ground out-of-tune signals. The coil is usually also adjustable (not shown), in order to widen or narrow the band-pass and to ensure that the ganged right-hand capacitors will be able to both match to the antenna and tune to the transceiver's operating frequency without compromising one or the other.
The functional description of the components is roughly correct, but too simple. In actual operation, the inductor and all of the capacitors interact to produce the overall result. Also, each of the components has small ‘parasitic’ impedances (as do all electrical parts) which affect the circuit at frequencies at the high end and low end of the circuit’s frequency range.
Ultimate Transmatch
Originally, the Ultimate Transmatch was promoted as a way to make the components more manageable at the lowest frequencies of interest and also to get some harmonic attenuation. The Ultimate Transmatch network resembles an SPC tuner with the input and output reversed. It is now considered obsolete; the design goals were better realized with the Series-Parallel Capacitor (SPC) network, shown above, which was designed after the name Ultimate had already been used.
Z match
The Z-Match is an ATU widely used for low-power amateur radio. This tuner uses a transformer on the output side, and thus can be easily used with either balanced or unbalanced transmission lines. It is limited in power output by the core used for the output transformer. The Z match has two tuning capacitors with separate connections to the primary transformer coil, producing two distinct resonant frequencies that enable it to cover a wide frequency range without switching the inductor.
Balanced line tuners
Balanced (open line) transmission lines require a tuner that has two "hot" output terminals, rather than one "hot" terminal and ground ("cold"). Since all modern transmitters have unbalanced (co-axial) output – almost always 50 Ohms – the most efficient system has the tuner provide a balun (balanced to unbalanced) transformation as well as providing an impedance match. The tuner usually includes a coil, and the coil can accept or produce either balanced or unbalanced input or output, depending on where the tap points are placed on the coil.
The following balanced circuit types have been used for tuners.
Referring to the adjacent diagram, the Fixed Link with Taps (top left) is the most basic circuit. The factor will be nearly constant and is set by the number of relative turns on the input link. The match is found by tuning the capacitor and selecting taps on the main coil, which may be done with a switch accessing various taps or by physically moving clips from turn to turn. If the turns on the main coil are changed to move to a higher or lower frequency, the link turns should also change.
The Hairpin tuner[14] (top right) has the same circuit, but uses a hairpin (transmission line) inductor. Moving the taps along the hairpin allows continuous adjustment of the impedance transformation, which is difficult with a solenoid coil. It is useful for very short wavelengths from about 10 meters to 70 cm (frequencies about 30 MHz to 430 MHz) where the solenoid inductor would have too few turns to allow fine adjustment. These tuners typically operate over at most a 2:1 frequency range.
Series Cap with Taps (middle, left). Adding a series capacitor to the input side of the Fixed Link with Taps allows fine adjustment with fewer taps on the main coil. An alternate connection (middle, right) for the series cap circuit is useful for low impedances only, but avoids the taps (For Low Z lines on the diagram).
Swinging Link with Taps (bottom left). A swinging link inserted into the Fixed Link With Taps also allows fine adjustment with fewer coil taps. The swinging link is a form of variable transformer, that moves the input coil in and out of the space between turns in the main coil to change their mutual inductance. The variable inductance makes these tuners more flexible than the basic circuit, but at some cost in complexity.
Fixed Link with Differential Capacitors (bottom right). The circuit with differential capacitors was the design used for the well-regarded Johnson Matchbox tuners. The four output capacitors (C2) are ganged, and as the top and bottom caps increase in value the two middle caps decrease in value. This provides a smooth change of loading that is equivalent to moving taps on the main coil. The Johnson Matchbox used a band switch to change the turns on the main and link inductors for each of the five frequency bands available to hams in the 1950s. The design has been criticized since the two middle-section capacitors in C2 are not strictly necessary to obtain a match; however, the middle sections conveniently limit the disturbance of the adjustment for C1 caused by changes to C2.
Unbalanced tuner and a balun
Another approach to feeding balanced lines is to use an unbalanced tuner with a balun on either the input (transmitter) or output (antenna) side of the tuner. Most often using the popular high pass T circuit described above, with either a 1:1 current balun on the input side of the unbalanced tuner or a balun (typically 4:1) on the output side. It can be managed, but doing so both efficiently and safely is not easy.
Balun between the antenna and the ATU
Any balun placed on the output (antenna) side of a tuner must be built to withstand high voltage and current stresses, because of the wide range of impedances it must handle.
For a wide range of frequencies and impedances it may not be possible to build a robust balun that is efficient enough. For a narrow range of frequencies, using transmission line stubs for impedance transforms (described above) may well be more feasible and will certainly be more efficient.
Balun between the transmitter and the ATU
The demands put on the balun are more modest if the balun is put on the input end of the tuner – between the tuner and the transmitter. Placed on that end it always operates into a constant 50 Ohm impedance from the transmitter on one side, and has the tuning circuit to protect it from wild swings in the feedline impedance on the other side. All to the good. Unfortunately, making the input from the transmitter balanced creates problems that must be remedied.
If an unbalanced tuner is fed with a balanced line from a balun instead of directly from the transmitter, then its normal antenna connection – the center wire of its output coaxial cable – provides the signal as usual to one side of the antenna. However the ground side of that same output connection must now feed an equal and opposite current to the other side of the antenna.
The two "hot" feeds must lie halfway between the "true" ground voltage at the antenna and transmitter: Inside the ATU, the matching circuit's "ground" level is equally different from the actual ground level on either the antenna or the transmitter side as the conventional "hot" wire is. Either the "hot" output wire or the matching circuit "ground" will give you exactly the same shock if you touch it.
The tuner circuit must "float" above or below the exterior ground level in order for the ATU circuit ground (or common side) to feed the second hot wire that formerly was attached to the output cable's ground wire: The circuit's floating ground must provide a voltage difference adequate to drive current through an output terminal to make the second output "hot".
High voltages are normal in any efficient impedance matching circuit bridging a wide mismatch. Unless the incompatible grounds are carefully kept separate the high voltages present between this interior floating ground and the exterior transmitter and antenna grounds can lead to arcing, corona discharge, capacitively coupled ground currents, and electric shock.
Keeping the mismatched grounds apart
To reduce power loss and protect the operator and the equipment, the tuner chassis must be double-layered: An outer chassis and an inner chassis. The outer chassis must enclose and insulate the tuning circuit and its floating ground from the outside, while itself remaining at the level of the exterior ground(s). With the protective outer chassis, the inner chassis can maintain its own incompatible "ground" level in isolation.
The inner chassis can be reduced to nothing more than a mounting platform inside the outer chassis, elevated on insulators to keep distance between the floating ground and the other electrical grounds that are connected to the outer chassis. The inner tuning circuit's metal mounting chassis, and in particular the metal rods connected to adjustment knobs on the outer chassis must all be kept separate from the surface touched by the operator and from direct electrical contact with the transmitter's ground on its connection cable.
Isolating the controls is usually done by replacing at least part of the connecting rods between knobs on the outside surface and adjustable parts on the inside platform with an insulated rod, either made of a sturdy ceramic or a plastic that tolerates high temperatures. Further, the metal inner and outer parts must be adequately distant to prevent current leaking out via capacitive coupling when the interior voltages are high. Finally, all these arrangements must be secured with greater than usual care, to ensure that jostling, pressure, or heat expansion cannot create a contact between the inner and outer grounds. This puts difficult constraints on the tuner's construction and high demands on the builder's craftsmanship.
Antenna system losses
Loss in Antenna tuners
Every means of impedance match will introduce some power loss. This will vary from a few percent for a transformer with a ferrite core, to 50% or more for a complicated ATU that is improperly tuned or working at the limits of its tuning range.
With the narrow band tuners, the L-network has the lowest loss, partly because it has the fewest components, but mainly because it necessarily operates at the lowest possible for a given impedance transformation. With the L-network, the loaded is not adjustable, but is fixed midway between the source and load impedances. Since most of the loss in practical tuners will be in the coil, changing from a low-pass to a high-pass circuit (or vice-versa) may reduce the loss a little.
The L-network using only capacitors will have the lowest loss, but this network only works where the load impedance is very inductive, making it a good choice for a small loop antenna. Inductive impedance also occurs with straight-wire antennas used at frequencies slightly above a resonant frequency, where the antenna is too long – for example, between a quarter and a half wave long at the operating frequency. However, problematic straight-wire antennas are typically too short for the frequency in use.
With the high-pass T-network, the loss in the tuner can vary from a few percent – if tuned for lowest loss – to over 50% if the tuner is not properly adjusted. Using the maximum available capacitance will give less loss, than if one simply tunes for a match without regard for the settings. This is because using more capacitance means using fewer inductor turns, and the loss is mainly in the inductor.
With the SPC tuner the losses will be somewhat higher than with the T-network, since the added capacitance across the inductor will shunt some reactive current to ground which must be cancelled by additional current in the inductor. The trade-off is that the effective inductance of the coil is increased, thus allowing operation at lower frequencies than would otherwise be possible.
If additional filtering is desired, the inductor can be deliberately set to larger values, thus providing a partial band pass effect. Either the high-pass T, low-pass π, or the SPC tuner can be adjusted in this manner. The additional attenuation at harmonic frequencies can be increased significantly with only a small percentage of additional loss at the tuned frequency.
When adjusted for minimum loss, the SPC tuner will have better harmonic rejection than the high-pass T due to its internal tank circuit. Either type is capable of good harmonic rejection if a small additional loss is acceptable. The low-pass π has exceptional harmonic attenuation at any setting, including the lowest-loss.
ATU location
An ATU will be inserted somewhere along the line connecting the radio transmitter or receiver to the antenna. The antenna feedpoint is usually high in the air (for example, a dipole antenna) or far away (for example, an end-fed random wire antenna). A transmission line, or feedline, must carry the signal between the transmitter and the antenna. The ATU can be placed anywhere along the feedline: at the transmitter, at the antenna, or somewhere in between.
Antenna tuning is best done as close to the antenna as possible to minimize loss, increase bandwidth, and reduce voltage and current on the transmission line. Also, when the information being transmitted has frequency components whose wavelength is a significant fraction of the electrical length of the feed line, distortion of the transmitted information will occur if there are standing waves on the line. Analog TV and FM stereo broadcasts are affected in this way. For those modes, matching at the antenna is required.
When possible, an automatic or remotely-controlled tuner in a weather-proof case at or near the antenna is convenient and makes for an efficient system. With such a tuner, it is possible to match a wide range of antennas (including stealth antennas).[
When the ATU must be located near the radio for convenient adjustment, any significant SWR will increase the loss in the feedline. For that reason, when using an ATU at the transmitter, low-loss, high-impedance feedline is a great advantage (open-wire line, for example). A short length of low-loss coaxial line is acceptable, but with longer lossy lines the additional loss due to SWR becomes very high.
It is very important to remember that when matching the transmitter to the line, as is done when the ATU is near the transmitter, there is no change in the SWR in the feedline. The backlash currents reflected from the antenna are retro-reflected by the ATU – usually several times between the two – and so are invisible on the transmitter-side of the ATU. The result of the multiple reflections is compounded loss, higher voltage or higher currents, and narrowed bandwidth, none of which can be corrected by the ATU.
Standing wave ratio
It is a common misconception that a high standing wave ratio (SWR) per se causes loss. A well-adjusted ATU feeding an antenna through a low-loss line may have only a small percentage of additional loss compared with an intrinsically matched antenna, even with a high SWR (4:1, for example). An ATU sitting beside the transmitter just re-reflects energy reflected from the antenna (“backlash current”) back yet again along the feedline to the antenna (“retro-reflection”). High losses arise from RF resistance in the feedline and antenna, and those multiple reflections due to high SWR cause feedline losses to be compounded.
Using low-loss, high-impedance feedline with an ATU results in very little loss, even with multiple reflections. However, if the feedline-antenna combination is ‘lossy’ then an identical high SWR may lose a considerable fraction of the transmitter's power output. High impedance lines – such as most parallel-wire lines – carry power mostly as high voltage rather than high current, and current alone determines the power lost to line resistance. So despite high SWR, very little power is lost in high-impedance line compared low-impedance line – typical coaxial cable, for example. For that reason, radio operators can be more casual about using tuners with high-impedance feedline.
Without an ATU, the SWR from a mismatched antenna and feedline can present an improper load to the transmitter, causing distortion and loss of power or efficiency with heating and/or burning of the output stage components. Modern solid state transmitters will automatically reduce power when challenged by a high SWR. Consequently, some solid-state power stages only produce weak signals if the SWR rises above 1.5 to 1. Were it not for that problem, even the losses from an SWR of 2:1 could be tolerated, since only 11 percent of transmitted power would be reflected and 89 percent sent out through to the antenna. So the main loss of power at high SWR is due to the transmitter ‘backing off’ its output power when confronted with backlash current.
Tube transmitters and amplifiers usually have an adjustable output network that can feed mismatched loads up to perhaps 3:1 SWR without trouble. In effect the built-in π-network of the transmitter output stage acts as an ATU. Further, since tubes are electrically robust (even though mechanically fragile), tube-based circuits can tolerate very high backlash current without damage.
Broadcast Applications
AM broadcast transmitters
One of the oldest applications for antenna tuners is in AM and shortwave broadcasting transmitters. AM transmitters usually use a vertical antenna (tower) which can be from 0.20 to 0.68 wavelengths long. At the base of the tower an ATU is used to match the antenna to the 50 Ohm transmission line from the transmitter. The most commonly used circuit is a T-network, using two series inductors with a shunt capacitor between them.
When multiple towers are used the ATU network may also provide for a phase adjustment so that the currents in each tower can be phased relative to the others to produce a signal in a desired direction. Stations are often required by law to prevent signals in directions that could produce interference with other stations. The transmitting station also benefits from an increase in signal power going to the station’s assigned target area. Adjustment of the ATUs in a multitower array is a complicated, time consuming process, requiring considerable expertise.
High-power shortwave transmitters
For international shortwave broadcasting (50 kW and above) stations change frequencies to better reach their target audience on a seasonal or even a daily basis, which requires frequent adjustment of antenna matching and phasing circuitry. Modern shortwave transmitters typically include built-in impedance-matching circuitry for SWR up to 2:1 , and can adjust their output impedance within 15 seconds.
The matching networks in transmitters sometimes incorporate a balun or an external one can be installed at the transmitter in order to feed a balanced line. Balanced transmission lines of 300 Ohms or more were more-or-less standard for all shortwave transmitters and antennas in the past, even by amateurs. Most shortwave broadcasters have continued to use high-impedance feeds even before the advent of automatic impedance matching.
The most commonly used shortwave antennas for international broadcasting are the HRS antenna (curtain array), which covers a 2 to 1 frequency range, and the log-periodic antenna, which can cover up to an 8 to 1 frequency range. Within the design range, the antenna SWR will vary, but these designs usually keep the SWR below 1.7 to 1 – easily within the range of SWR that can be tuned by built-in antenna matching in many modern transmitters. So when feeding well-chosen antennas, a modern transmitter will be able to adjust itself as needed to match to the antenna at any frequency.
XXX . XXX 4%zero null 0 Smith chart
The Smith chart, invented by Phillip H. Smith (1905–1987), is a graphical aid or nomogram designed for electrical and electronics engineers specializing in radio frequency (RF) engineering to assist in solving problems with transmission lines and matching circuits. The Smith chart can be used to simultaneously display multiple parameters including impedances, admittances, reflection coefficients, scattering parameters, noise figure circles, constant gain contours and regions for unconditional stability, including mechanical vibrations analysis. The Smith chart is most frequently used at or within the unity radius region. However, the remainder is still mathematically relevant, being used, for example, in oscillator design and stability analysis.
While the use of paper Smith charts for solving the complex mathematics involved in matching problems has been largely replaced by software based methods, the Smith chart display is still the preferred method of displaying how RF parameters behave at one or more frequencies, an alternative to using tabular information. Thus most RF circuit analysis software includes a Smith chart option for the display of results and all but the simplest impedance measuring instruments can display measured results on a Smith chart display.

An impedance Smith chart (with no data plotted)
Overview
The Smith chart is plotted on the complex reflection coefficient plane in two dimensions and is scaled in normalised impedance (the most common), normalised admittance or both, using different colours to distinguish between them. These are often known as the Z, Y and YZ Smith charts respectively.[7] Normalised scaling allows the Smith chart to be used for problems involving any characteristic or system impedance which is represented by the center point of the chart. The most commonly used normalization impedance is 50 ohms. Once an answer is obtained through the graphical constructions described below, it is straightforward to convert between normalised impedance (or normalised admittance) and the corresponding unnormalized value by multiplying by the characteristic impedance (admittance). Reflection coefficients can be read directly from the chart as they are unitless parameters.
The Smith chart has circumferential scaling in wavelengths and degrees. The wavelengths scale is used in distributed component problems and represents the distance measured along the transmission line connected between the generator or source and the load to the point under consideration. The degrees scale represents the angle of the voltage reflection coefficient at that point. The Smith chart may also be used for lumped element matching and analysis problems.
Use of the Smith chart and the interpretation of the results obtained using it requires a good understanding of AC circuit theory and transmission line theory, both of which are pre-requisites for RF engineers.
As impedances and admittances change with frequency, problems using the Smith chart can only be solved manually using one frequency at a time, the result being represented by a point. This is often adequate for narrow band applications (typically up to about 5% to 10% bandwidth) but for wider bandwidths it is usually necessary to apply Smith chart techniques at more than one frequency across the operating frequency band. Provided the frequencies are sufficiently close, the resulting Smith chart points may be joined by straight lines to create a locus.
A locus of points on a Smith chart covering a range of frequencies can be used to visually represent:
- how capacitive or how inductive a load is across the frequency range
- how difficult matching is likely to be at various frequencies
- how well matched a particular component is.
The accuracy of the Smith chart is reduced for problems involving a large locus of impedances or admittances, although the scaling can be magnified for individual areas to accommodate these.
Mathematical basis
Actual and normalised impedance and admittance[edit]
A transmission line with a characteristic impedance of may be universally considered to have a characteristic admittance of where
Any impedance, expressed in ohms, may be normalised by dividing it by the characteristic impedance, so the normalised impedance using the lower case zT is given by
Similarly, for normalised admittance
The SI unit of impedance is the ohm with the symbol of the upper case Greek letter omega (Ω) and the SI unit for admittance is the siemens with the symbol of an upper case letter S. Normalised impedance and normalised admittance are dimensionless. Actual impedances and admittances must be normalised before using them on a Smith chart. Once the result is obtained it may be de-normalised to obtain the actual result.
The normalised impedance Smith chart
Using transmission line theory, if a transmission line is terminated in an impedance () which differs from its characteristic impedance (), a standing wave will be formed on the line comprising the resultant of both the incident or forward () and the reflected or reversed () waves. Using complex exponential notation:
- and
where
- is the temporal part of the wave
- is the spatial part of the wave and
- where
- is the angular frequency in radians per second (rad/s)
- is the frequency in hertz (Hz)
- is the time in seconds (s)
- and are constants
- is the distance measured along the transmission line from the load toward the generator in metres (m)
Also
- is the propagation constant which has units 1/m
where
- is the attenuation constant in nepers per metre (Np/m)
- is the phase constant in radians per metre (rad/m)
The Smith chart is used with one frequency () at a time, and only for one moment () at a time, so the temporal part of the phase () is fixed. All terms are actually multiplied by this to obtain the instantaneous phase, but it is conventional and understood to omit it. Therefore,
- and
where and are respectively the forward and reverse voltage amplitudes at the load.
The variation of complex reflection coefficient with position along the line
The complex voltage reflection coefficient is defined as the ratio of the reflected wave to the incident (or forward) wave. Therefore,
where C is also a constant.
For a uniform transmission line (in which is constant), the complex reflection coefficient of a standing wave varies according to the position on the line. If the line is lossy ( is non-zero) this is represented on the Smith chart by a spiral path. In most Smith chart problems however, losses can be assumed negligible () and the task of solving them is greatly simplified. For the loss free case therefore, the expression for complex reflection coefficient becomes
where is the reflection coefficient at the load, and is the line length from the load to the location where the reflection coefficient is measured. The phase constant may also be written as
where is the wavelength within the transmission line at the test frequency.
Therefore,
This equation shows that, for a standing wave, the complex reflection coefficient and impedance repeats every half wavelength along the transmission line. The complex reflection coefficient is generally simply referred to as reflection coefficient. The outer circumferential scale of the Smith chart represents the distance from the generator to the load scaled in wavelengths and is therefore scaled from zero to 0.50 .
The variation of normalised impedance with position along the line
If and are the voltage across and the current entering the termination at the end of the transmission line respectively, then
- and
- .
By dividing these equations and substituting for both the voltage reflection coefficient
and the normalised impedance of the termination represented by the lower case z, subscript T
gives the result:
- .
Alternatively, in terms of the reflection coefficient
These are the equations which are used to construct the Z Smith chart. Mathematically speaking and are related via a Möbius transformation.
Both and are expressed in complex numbers without any units. They both change with frequency so for any particular measurement, the frequency at which it was performed must be stated together with the characteristic impedance.
may be expressed in magnitude and angle on a polar diagram. Any actual reflection coefficient must have a magnitude of less than or equal to unity so, at the test frequency, this may be expressed by a point inside a circle of unity radius. The Smith chart is actually constructed on such a polar diagram. The Smith chart scaling is designed in such a way that reflection coefficient can be converted to normalised impedance or vice versa. Using the Smith chart, the normalised impedance may be obtained with appreciable accuracy by plotting the point representing the reflection coefficient treating the Smith chart as a polar diagram and then reading its value directly using the characteristic Smith chart scaling. This technique is a graphical alternative to substituting the values in the equations.
By substituting the expression for how reflection coefficient changes along an unmatched loss free transmission line
for the loss free case, into the equation for normalised impedance in terms of reflection coefficient
- .
and using Euler's formula
yields the impedance version transmission line equation for the loss free case:
where is the impedance 'seen' at the input of a loss free transmission line of length , terminated with an impedance
Versions of the transmission line equation may be similarly derived for the admittance loss free case and for the impedance and admittance lossy cases.
The Smith chart graphical equivalent of using the transmission line equation is to normalise , to plot the resulting point on a Z Smith chart and to draw a circle through that point centred at the Smith chart centre. The path along the arc of the circle represents how the impedance changes whilst moving along the transmission line. In this case the circumferential (wavelength) scaling must be used, remembering that this is the wavelength within the transmission line and may differ from the free space wavelength.
Regions of the Z Smith chart
If a polar diagram is mapped on to a cartesian coordinate system it is conventional to measure angles relative to the positive x-axis using a counterclockwise direction for positive angles. The magnitude of a complex number is the length of a straight line drawn from the origin to the point representing it. The Smith chart uses the same convention, noting that, in the normalised impedance plane, the positive x-axis extends from the center of the Smith chart at to the point . The region above the x-axis represents inductive impedances (positive imaginary parts) and the region below the x-axis represents capacitive impedances (negative imaginary parts).
If the termination is perfectly matched, the reflection coefficient will be zero, represented effectively by a circle of zero radius or in fact a point at the centre of the Smith chart. If the termination was a perfect open circuit or short circuit the magnitude of the reflection coefficient would be unity, all power would be reflected and the point would lie at some point on the unity circumference circle.
Circles of constant normalised resistance and constant normalised reactance
The normalised impedance Smith chart is composed of two families of circles: circles of constant normalised resistance and circles of constant normalised reactance. In the complex reflection coefficient plane the Smith chart occupies a circle of unity radius centred at the origin. In cartesian coordinates therefore the circle would pass through the points (+1,0) and (−1,0) on the x-axis and the points (0,+1) and (0,−1) on the y-axis.
Since both and are complex numbers, in general they may be written as:
with a, b, c and d real numbers.
Substituting these into the equation relating normalised impedance and complex reflection coefficient:
gives the following result:
- .
This is the equation which describes how the complex reflection coefficient changes with the normalised impedance and may be used to construct both families of circles.
The Y Smith chart
The Y Smith chart is constructed in a similar way to the Z Smith chart case but by expressing values of voltage reflection coefficient in terms of normalised admittance instead of normalised impedance. The normalised admittance yT is the reciprocal of the normalised impedance zT, so
Therefore:
and
The Y Smith chart appears like the normalised impedance type but with the graphic scaling rotated through 180°, the numeric scaling remaining unchanged.
The region above the x-axis represents capacitive admittances and the region below the x-axis represents inductive admittances. Capacitive admittances have positive imaginary parts and inductive admittances have negative imaginary parts.
Again, if the termination is perfectly matched the reflection coefficient will be zero, represented by a 'circle' of zero radius or in fact a point at the centre of the Smith chart. If the termination was a perfect open or short circuit the magnitude of the voltage reflection coefficient would be unity, all power would be reflected and the point would lie at some point on the unity circumference circle of the Smith chart.
Practical examples
A point with a reflection coefficient magnitude 0.63 and angle 60° represented in polar form as , is shown as point P1 on the Smith chart. To plot this, one may use the circumferential (reflection coefficient) angle scale to find the graduation and a ruler to draw a line passing through this and the centre of the Smith chart. The length of the line would then be scaled to P1 assuming the Smith chart radius to be unity. For example, if the actual radius measured from the paper was 100 mm, the length OP1 would be 63 mm.
The following table gives some similar examples of points which are plotted on the Z Smith chart. For each, the reflection coefficient is given in polar form together with the corresponding normalised impedance in rectangular form. The conversion may be read directly from the Smith chart or by substitution into the equation.
| Point Identity | Reflection Coefficient (Polar Form) | Normalised Impedance (Rectangular Form) |
|---|---|---|
| P1 (Inductive) | ||
| P2 (Inductive) | ||
| P3 (Capacitive) |
Working with both the Z Smith chart and the Y Smith charts
In RF circuit and matching problems sometimes it is more convenient to work with admittances (representing conductances and susceptances) and sometimes it is more convenient to work with impedances (representing resistances and reactances). Solving a typical matching problem will often require several changes between both types of Smith chart, using normalised impedance for series elements and normalised admittances for parallel elements. For these a dual (normalised) impedance and admittance Smith chart may be used. Alternatively, one type may be used and the scaling converted to the other when required. In order to change from normalised impedance to normalised admittance or vice versa, the point representing the value of reflection coefficient under consideration is moved through exactly 180 degrees at the same radius. For example, the point P1 in the example representing a reflection coefficient of has a normalised impedance of . To graphically change this to the equivalent normalised admittance point, say Q1, a line is drawn with a ruler from P1 through the Smith chart centre to Q1, an equal radius in the opposite direction. This is equivalent to moving the point through a circular path of exactly 180 degrees. Reading the value from the Smith chart for Q1, remembering that the scaling is now in normalised admittance, gives . Performing the calculation
manually will confirm this.
Once a transformation from impedance to admittance has been performed the scaling changes to normalised admittance until such time that a later transformation back to normalised impedance is performed.
The table below shows examples of normalised impedances and their equivalent normalised admittances obtained by rotation of the point through 180°. Again these may either be obtained by calculation or using a Smith chart as shown, converting between the normalised impedance and normalised admittances planes.
| Normalised Impedance Plane | Normalised Admittance Plane |
|---|---|
| P1 () | Q1 () |
| P10 () | Q10 () |
Choice of Smith chart type and component type
The choice of whether to use the Z Smith chart or the Y Smith chart for any particular calculation depends on which is more convenient. Impedances in series and admittances in parallel add while impedances in parallel and admittances in series are related by a reciprocal equation. If is the equivalent impedance of series impedances and is the equivalent impedance of parallel impedances, then
For admittances the reverse is true, that is
Dealing with the reciprocals, especially in complex numbers, is more time consuming and error-prone than using linear addition. In general therefore, most RF engineers work in the plane where the circuit topography supports linear addition. The following table gives the complex expressions for impedance (real and normalised) and admittance (real and normalised) for each of the three basic passive circuit elements: resistance, inductance and capacitance. Using just the characteristic impedance (or characteristic admittance) and test frequency an equivalent circuit can be found and vice versa.
| Element Type | Impedance (Z or z) or Reactance (X or x) | Admittance (Y or y) or Susceptance (B or b) | ||
|---|---|---|---|---|
| Real () | Normalised (No Unit) | Real (S) | Normalised (No Unit) | |
| Resistance (R) | ||||
| Inductance (L) | ||||
| Capacitance (C) | ||||
Using the Smith chart to solve conjugate matching problems with distributed components
Distributed matching becomes feasible and is sometimes required when the physical size of the matching components is more than about 5% of a wavelength at the operating frequency. Here the electrical behaviour of many lumped components becomes rather unpredictable. This occurs in microwave circuits and when high power requires large components in shortwave, FM and TV Broadcasting,
For distributed components the effects on reflection coefficient and impedance of moving along the transmission line must be allowed for using the outer circumferential scale of the Smith chart which is calibrated in wavelengths.
The following example shows how a transmission line, terminated with an arbitrary load, may be matched at one frequency either with a series or parallel reactive component in each case connected at precise positions.
Supposing a loss-free air-spaced transmission line of characteristic impedance , operating at a frequency of 800 MHz, is terminated with a circuit comprising a 17.5 resistor in series with a 6.5 nanohenry (6.5 nH) inductor. How may the line be matched?
From the table above, the reactance of the inductor forming part of the termination at 800 MHz is
so the impedance of the combination () is given by
and the normalised impedance () is
This is plotted on the Z Smith chart at point P20. The line OP20 is extended through to the wavelength scale where it intersects at the point . As the transmission line is loss free, a circle centred at the centre of the Smith chart is drawn through the point P20 to represent the path of the constant magnitude reflection coefficient due to the termination. At point P21 the circle intersects with the unity circle of constant normalised resistance at
- .
The extension of the line OP21 intersects the wavelength scale at , therefore the distance from the termination to this point on the line is given by
Since the transmission line is air-spaced, the wavelength at 800 MHz in the line is the same as that in free space and is given by
where is the velocity of electromagnetic radiation in free space and is the frequency in hertz. The result gives , making the position of the matching component 29.6 mm from the load.
The conjugate match for the impedance at P21 () is
As the Smith chart is still in the normalised impedance plane, from the table above a series capacitor is required where
Rearranging, we obtain
- .
Substitution of known values gives
To match the termination at 800 MHz, a series capacitor of 2.6 pF must be placed in series with the transmission line at a distance of 29.6 mm from the termination.
An alternative shunt match could be calculated after performing a Smith chart transformation from normalised impedance to normalised admittance. Point Q20 is the equivalent of P20 but expressed as a normalised admittance. Reading from the Smith chart scaling, remembering that this is now a normalised admittance gives
(In fact this value is not actually used). However, the extension of the line OQ20 through to the wavelength scale gives . The earliest point at which a shunt conjugate match could be introduced, moving towards the generator, would be at Q21, the same position as the previous P21, but this time representing a normalised admittance given by
- .
The distance along the transmission line is in this case
which converts to 123 mm.
The conjugate matching component is required to have a normalised admittance () of
- .
From the table it can be seen that a negative admittance would require an inductor, connected in parallel with the transmission line. If its value is , then
This gives the result
A suitable inductive shunt matching would therefore be a 6.5 nH inductor in parallel with the line positioned at 123 mm from the load.
Using the Smith chart to analyze lumped element circuits
The analysis of lumped element components assumes that the wavelength at the frequency of operation is much greater than the dimensions of the components themselves. The Smith chart may be used to analyze such circuits in which case the movements around the chart are generated by the (normalized) impedances and admittances of the components at the frequency of operation. In this case the wavelength scaling on the Smith chart circumference is not used. The following circuit will be analyzed using a Smith chart at an operating frequency of 100 MHz. At this frequency the free space wavelength is 3 m. The component dimensions themselves will be in the order of millimetres so the assumption of lumped components will be valid. Despite there being no transmission line as such, a system impedance must still be defined to enable normalization and de-normalization calculations and is a good choice here as . If there were very different values of resistance present a value closer to these might be a better choice.
The analysis starts with a Z Smith chart looking into R1 only with no other components present. As is the same as the system impedance, this is represented by a point at the centre of the Smith chart. The first transformation is OP1 along the line of constant normalized resistance in this case the addition of a normalized reactance of -j0.80, corresponding to a series capacitor of 40 pF. Points with suffix P are in the Z plane and points with suffix Q are in the Y plane. Therefore, transformations P1 to Q1 and P3 to Q3 are from the Z Smith chart to the Y Smith chart and transformation Q2 to P2 is from the Y Smith chart to the Z Smith chart. The following table shows the steps taken to work through the remaining components and transformations, returning eventually back to the centre of the Smith chart and a perfect 50 ohm match.
| Transformation | Plane | x or y Normalized Value | Capacitance/Inductance | Formula to Solve | Result |
|---|---|---|---|---|---|
| Capacitance (Series) | |||||
| Inductance (Shunt) | |||||
| Z | Capacitance (Series) | ||||
| Y | Capacitance (Shunt) |
3D Smith chart
A generalized 3D Smith chart based on the extended complex plane (Riemann sphere) and inversive geometry was proposed in 2011. The chart unifies the passive and active circuit design on little and big circles on the surface of a unit sphere using the stereographic conformal map of the reflection coefficient's generalized plane. Considering the point at infinity, the space of the new chart includes all possible loads. The north pole is the perfect matching point, while the south pole is the perfect mismatch point.
XXX . XXX 4%zero null 0 1 2 3 Antenna Terminology Defined
Antenna theory and antenna terminology can seem complicated to the uninitiated. A lot goes into designing antennas but with a little bit of guidance and explanation, antenna users (network designers, systems integrators, end users) can read through the antenna specifications and choose the right antenna style for their wireless network design.
In this paper we will go over some simple techniques to help you better understand some terminologyused and how it is applied in the Antenna industry. This will be part one of a two part series white paper. Part two will cover more advanced details. Both parts will provide the reader a wealth of knowledge that is essential for antenna selection and solutions.
So let’s get started. The Antenna Radiation Pattern is a graphical representation of the antennas radiated electrical performance. This wave of energy (electromagnetic in origin) emitted from the antenna that propagates through space is measured at a defined Angle, Amplitude, and Frequency. The measurement of this performance is commonly presented in a graphical format.
Let’s look at an Omni-directional antenna example: Think of the ripple that is created when a person throws a stone in the middle of a calm body of water (such as a pond). As the rock enters the water it causes the water all around it to rise and creates a ripple in the water.
• Think of this ripple as the “WAVE”.
• Think of the “FREQUENCY” as the number of the waves or the occurrences where the wave repeats over a period of time (from the stone to the shore).
• Think of the size in height of the wave as the “AMPLITUDE”, and
• Think of the length of the wave as the “WAVELENGTH”.
• As this wave moves outward away from the rock’s point of entry and towards the shore, the migration of this wave is called “PROPAGATION”.
Think of the letter “S” turned sideways to get a visual image of the peaks and valleys of the propagation wave. If this wave were to get smaller or squeezed and the “amount of occurrences increased” that would indicate that the frequency is getting higher. If this wave were to be stretched out longer and the “amount of occurrences decreased” then we can relate to the frequency becoming lower.
Here is an illustration that represents a “Low Frequency” vs. “High Frequency” wave.
To best describe the “ANGLE” we will approach this in two ways “Omni-directional” & “Directional”. First think of the “ANGLE” as the direction of the wave that is traveling from the rock. (Looking down from above) as shown in Fig (1a.)
The first way- Example (1) shows an “Omni-directional” wave where the wave is traveling from the rock to the shore equally in all directions.
The second way-Example (2) shows a “Directional” wave where the wave is traveling from the rock to the shore in a defined direction.
In both examples substitute the rock for an antenna. You can now visualize the Omni-directional and Directional antenna wave. The measurement around this wave represents the “Azimuth” angle direction. (Similar to how one reads a compass)
Next we will identify is the “Elevation” angle. This is the “Up” and “Down” angle from a reference plane, generally the horizon (such as the surface of the pond). For example, if you were looking through an aquarium window and the surface of the water was at eye level. Looking up you could see the sky, and looking down you could see the bottom of the aquarium. This is the elevation angle. Then look to the left or right. This is a change in Azimuth angle. So you can see there are multiple combination angles you can have.
Understanding angle in relation to an antenna pattern is a key factor. Using this knowledge is beneficial for selecting the type of antenna needed to achieve the coverage you desire.
For example, the network design may require that an antenna be placed upon a water tower to provide coverage close in or at a moderate distance for all of the homes around the tower. Or, the network design may require that an antenna be placed upon a water tower to provide coverage of a small patch of manufacturing shops with the additional requirement that the radiated signal not go outside this area.
As you can see these are two different antenna requirements. Having the ability to select the type of antenna and a general understanding of angles associated (elevation and azimuth patterns) are vital.
The first antenna upon the water tower would be an Omni-directional antenna. This will provide coverage around the water tower (Azimuth). Knowing the angles from where the antenna will be located to the closest subscriber and the furthest is needed. These angles will then be used to select the proper antenna elevation pattern needed for best coverage.
The second antenna upon the tower would most likely be a directional type. Typically a panel, parabolic, yagi, or log periodic style antenna that has the ability to focus the radiated energy. This will have a narrow azimuth beam width and a narrow elevation beam width.
If you were to look at a side view (2D) of the first antenna (Omni-directional) this is what the elevation radiation pattern would look like reference to the elevation angle.
 Now let’s look at one other terms used that I did not mention above: “Phase”. Phase is a complex function of the antenna and the surroundings. In this paper we will not discuss phase in great detail, but cover the general idea. Phase is an important factor and prior to antenna placement one should have a little understanding of its role. Having a little knowledge beforehand could save you from placing the antenna in an undesired location or configuration that affects the system performance. Phase can be constructive or destructive, by allowing the antenna to work well in performance or be destructive where it severely affects the antennas performance.
Now let’s look at one other terms used that I did not mention above: “Phase”. Phase is a complex function of the antenna and the surroundings. In this paper we will not discuss phase in great detail, but cover the general idea. Phase is an important factor and prior to antenna placement one should have a little understanding of its role. Having a little knowledge beforehand could save you from placing the antenna in an undesired location or configuration that affects the system performance. Phase can be constructive or destructive, by allowing the antenna to work well in performance or be destructive where it severely affects the antennas performance.
A good example would be an antenna on the roof top with nothing around it. The signal from the antenna would propagate well. If a maintenance worker placed a large pipe right next to the antenna of equal height at ½ wavelengths away (meaning 180° in phase), the signal propagated from the antenna would reflect back off this pipe and affect the propagated wave, typically in a destructive fashion. This reflection would cause cancelation, reduction in signal, or blockage. This would be considered a destructive reflection. So if you had an Omni-directional antenna in this configuration (no-pipe) and established communication link “in one particular direction” with good signal reception, when the pipe is placed in position, the signal can be affected so greatly that a loss of communication takes place in one or multiple directions.
However, a good example of constructive phase is where a ¼ wave monopole antenna is placed just over the surface of a ground plane commonly found as the whip antenna on automobiles. Seen in (Fig 4.) and the antenna uses the reflection created by the ground plane to establish good performance. If the ¼ wave antenna were to be placed at ½ wavelength distance above the ground plane (or 180° in phase) with a large gap between, then the antenna would not work effectively. This would result in a destructive phase contribution, typically affecting the radiation pattern and the (VSWR) tuning of the antenna. Known as the “Match”. The more destructive the reflection, the greater the signal loss or the slower data performance. We will use Fig (2.) to best illustrate what phase looks like graphically. Looking at this illustration you will see a line that has smooth repetitive oscillation (up and down), commonly called a sine wave or sinusoid. Note this sinusoidal line shape that has a start and a finish.
Think of the start being 0 and the end being 360. So if you were to place numbers equally spaced along this line you would have 0, 1, 2,3,4,5 etc all the way to 360. Add a degrees symbol (°) after each number and you will have the phase degrees identified over the length of this line. Now think of this line length from start to finish representing one wavelength. Below we will segment the wavelength into four equal sections. (In scientific term wavelength is identified by this symbol “λ” known as Lambda) phase is an “electrical” measurement in degrees” °” over the length of the wave.
Here we will place four points equally along this line. (4 equal sections as shown in illustration Fig (3.)

Fig (3.)
In Fig (3.) the four points represent 0°, 90°, 180°, 270°, and 360° in phase. Think of the 360° point, the start of a new cycle (occurrence) or where 0° begins again and then repeats as shown in (Fig 1.).
Think of 90° as a ¼ wavelength, 180° as a ½ wavelength, 270° as a ¾ wavelength, and 360° as one full wavelength. So we can envision when someone talks about quarter wave antenna.
For example: A “Rubber Duck Antenna” or ¼ wave monopole over a ground plane. Think of the ground plane being a metal roof of a vehicle and place the Rubber Duck antenna in the center with the antenna top end pointing straight up. See Fig (4.)
Fig (4.)
The wavelength corresponds to the velocity (speed) of the wave divided by its frequency. Below I will show you a simple formula that further explains how to calculate a wavelength for a given frequency. Using this formula will help you determine the wave length for a given frequency and you now have the ability to relate the phase. This is very helpful for antenna placement as mentioned above (constructive or destructive phase). For example: If the antenna manufacturer recommended a 2400 MHz Omni-directional antenna not to be placed closer than 10 wavelengths to the side of a utility shelter, you could then calculate what 10 wavelengths would be in inches.
11802.8 / Frequency in MHz = wavelength in inches. (in air)
Thus, 11802.8 / 2400 MHz is 4.917” or 4.917”=1 λ (One wavelength long)
Then 4.917 x 10 (wave lengths) = 49” inches
So the antenna needs to be at least 49” inches away from the utility shelter.
Let’s say, we have a special antenna and the frequency is 11,800 MHz and the wavelength is 1” in long, then we partition into four equal segments. We will have 0, ¼ ½ ¾ 1.
¼” represents ¼ λ (wavelength) and 90° in phase
½ presents ½ λ (wavelength) and 180° in phase
¾” represents ¾ λ (wavelength) and 270° in phase
1” represents 1 λ (wavelength) and 360° in phase
And the antenna manufacturer requires the antenna be placed at 360° in phase from the reflector for best performance; otherwise the radiation pattern will be severely distorted from a destructive phase contribution.
What is the distance you would select?
If you selected that the antenna placement would be 1” than you made the right choice.
Remember λ represents “Lambda” or wavelength. This symbol comes from the Greek alphabet and is used in antenna terminology quite often.
Digesting the knowledge we gained, let’s move on to what an antenna is.
An “Antenna” is a transducer or a device, designed to transmit or receive electromagnetic waves. Think of the “waves” we discussed above. Now if those waves were moving towards the antenna and the antenna received them, the antenna would convert those waves into electrical currents that the radio would use.
For example: In the first paragraph of this article, if the waves came from the shore to the stone, the stone would translate the waves (ripple) into a media that could be interpolated. Or another way to look at this is: The Radio inside a vehicle operates at a certain “Frequency” and produces a “Signal” that travels through a piece of coax to the antenna which converts the signal into an “Electromagnetic Wave” that is propagated outward. This is better known as “Radiated Energy”. The way the antenna radiates this energy or receives it is a function of its performance and is useful knowledge when selecting your antenna.
To convert the way the antenna radiates this energy or receives it to a form which we can understand and graph, an “Anechoic Chamber” is typically used for the measurement and test equipment used for interpolation. (Anechoic Chamber meaning a shielded room designed to measure electromagnetic energy. i.e. “measurement of the propagated wave in an electrically quiet area”). The antenna, which would be passive in nature, is typically measured by receiving a signal from a known source. Passive meaning there are no electronics added to the antenna that regulate the gain (amplitude) and the antenna works the same in both receiving and transmitting the signal. For active, think of a GPS that has additional electronics that amplifies the signal it receives and is not used for transmitting. This would be considered an active antenna. So let’s go back to the measurement.
When the antenna is placed in the Anechoic Chamber and measured, the measurement is then converted through electrical test equipment and mathematical functions.
The product that is produced is typically graphed so we can understand the performance. Generally called a “Radiation Pattern Plot”. The radiation Pattern Plot is usually presented in a Polar style plot or Rectangular style plot shown in Fig (5.)
Looking at the polar plot in Fig (5.) think of the Omni-directional antenna placed upon the vehicles roof as shown in Fig (4.). Now picture as if you were 100 feet above the car looking straight down. Place the car in the middle of the polar plot as shown in Fig (6.)
The plotted circle indicated by the arrow would be a good example of the horizontal radiation pattern of an Omni-Directional antenna.
See Fig (7.) ”Azimuth” for a better example of parallel to the earth’s horizon.
Fig (7.)
Now that we understand the polar plot, let’s discuss an easy way to understand the rectangular plot. If we were to think of the polar plot being a circle and we cut the circle, then straightened out the circle to form a straight line. It would look something like this Fig (8.) Now apply this to an X, Y graph as viewed in Fig (5.) Very simple! Another example would be a world map compared to a globe. One is flat (rectangular) and the other is round (polar). The equator is a round circle indicated on the globe and the equator is a straight line indicated on a map from one end to the other. There you have it.
Now apply this to an X, Y graph as viewed in Fig (5.) Very simple! Another example would be a world map compared to a globe. One is flat (rectangular) and the other is round (polar). The equator is a round circle indicated on the globe and the equator is a straight line indicated on a map from one end to the other. There you have it.
 Now apply this to an X, Y graph as viewed in Fig (5.) Very simple! Another example would be a world map compared to a globe. One is flat (rectangular) and the other is round (polar). The equator is a round circle indicated on the globe and the equator is a straight line indicated on a map from one end to the other. There you have it.
Now apply this to an X, Y graph as viewed in Fig (5.) Very simple! Another example would be a world map compared to a globe. One is flat (rectangular) and the other is round (polar). The equator is a round circle indicated on the globe and the equator is a straight line indicated on a map from one end to the other. There you have it.
Continuing on we need to understand what an “Elevation Pattern” is. Just like the azimuth pattern the elevation pattern is an important part. You cannot have one without the other. Refer to Fig (7.) and locate the elevation label. As you will notice the arrow goes up and down and is referenced to the horizon. This is how the radiation pattern will be referenced.
Let’s look at a few more examples to better clarify. Fig (9.) is a good representation of an Omni-directional antenna mounted on a vehicle roof that highlights both the elevation and the azimuth radiated energy.

Fig (9.)
So if we were to look at one slice of the elevation radiated energy See Fig (10.) then plot it in polar format. It would look something like this.
Fig (10.)
Here the elevation pattern is plotted and gives us a good representation of the vertical radiation from the antenna. It is typically plotted out in both rectangular and polar formats. More common is the polar format. Shown in Fig (9.) is a good representation of both the vertical and horizontal radiated energy in a 3 dimensional view. So when we look at the polar plot, it should be properly labeled “Elevation” or “Azimuth” and will give us a graphical representation of the antennas “propagation performance” referenced to the earth’s horizon.
we will focus more on antenna challenges. Mobile Mark, Inc. designs, manufactures and delivers top technology antenna products for the global telecommunications industry. Established in 1984 and located just outside Chicago, Mobile Mark is recognized as having the experience and professionalism needed to make it all happen. We offer innovative designs, quality manufacturing, and reliable performance. Mobile Mark helps companies understand the antenna theory and antenna terminology behind the antennas for optimum wireless network coverage.
- What is an antenna?
The antenna is a very important element of radio equipment.
The antenna of the transmitter emits high frequency energy into space while the antenna of the receiver catches this and converts it into electricity.
If the antenna is not precisely the right length for the frequency used, the radio waves cannot be emitted or captured efficiently. It should neither be too long, nor too short. A good transmitting antenna can be a good receiving antenna, and for ordinary uses, one antenna serves both functions.
Radio modules with antennas attached come equipped with an efficient antenna, and in some cases you may not be able to replace it with another antenna due to regulations in the Wireless Telegraphy Act. However, if you are designing equipment that includes a design for an antenna, or you are using a reception-only module, it is possible to use an antenna with gain (a gain antenna), so it is necessary for you to investigate the situation regarding antennas in detail.
The antenna of the transmitter emits high frequency energy into space while the antenna of the receiver catches this and converts it into electricity.
If the antenna is not precisely the right length for the frequency used, the radio waves cannot be emitted or captured efficiently. It should neither be too long, nor too short. A good transmitting antenna can be a good receiving antenna, and for ordinary uses, one antenna serves both functions.
Radio modules with antennas attached come equipped with an efficient antenna, and in some cases you may not be able to replace it with another antenna due to regulations in the Wireless Telegraphy Act. However, if you are designing equipment that includes a design for an antenna, or you are using a reception-only module, it is possible to use an antenna with gain (a gain antenna), so it is necessary for you to investigate the situation regarding antennas in detail.
The antenna mechanism

We introduced the formula for the wave length of radio waves in the previous section. An antenna which will be most efficient is an antenna with a length half the wave length of the frequency used. For example, if you are using a frequency of 433 MHz, the wave length is about 70 cm, therefore an antenna with a length of about 35 cm will be most efficient. The transmitter must emit radio waves using limited power, and the receiver must capture efficiently the radio waves that are emitted. With the antenna at this length, the antenna and transmitted radio waves achieve a resonant state and maximum power is emitted. At the receiver too, the received radio waves and antenna achieve a resonant state, and can capture the maximum power. The antenna should be kept as straight as possible and should not be bent into a circle. Today equipment tends to be compact, and antennas with a length ¼ (λ/4) that of the wave length are frequently used. The thinking behind λ/4 ground antennas is the same as for λ/2 dipole antennas. However as the function of one side is changed to earth, the antenna length is halved making a 1/4 λ antenna. For this reason, this earth is very important. The whip antennas of radio modules, mobile phones and so on use this mechanism, with the case serving the function of the ground.
 |  |
Types of antenna

The types of antenna include whip antennas, dipole antennas, Yagi-Uda arrays, parabola antennas, loop antennas and so on.
| Whip (rod) antennas | Antennas used for mobile phones and the like. Non-directional antenna with equal sensitivity in any direction. |
| Dipole antenna | Used for amateur radio and so on. |
| Yagi-Uda array | Used as television antennas and so on. They have strong directivity, and must be aligned in the direction of the transmitting station. This is a dipole antenna with director and reflector elements attached to direct and reflect the radio wave. |
| Parabola antenna | Used for receiving satellite broadcasts. These antennas have very strong directivity and require fine directional adjustment, but they can use the power of the radio waves efficiently. |
| Loop antenna | Loop antennas capture the changes in the magnetic field of the radio waves. The radio waves propagate in the direction at right angles to the circle of the loop. Similarly the receiving antenna is placed in such a way as to be perpendicular to the magnetic field of the radio waves. |
| Dielectric antenna | Antennas using high frequency dielectric ceramics can be compact and achieve high performance. |
Directional pattern of antennas

There are both directional antennas and non-directional antennas. Antennas with directivity are used in cases where the direction of the other party in communication is fixed. This avoids unwanted radio wave emission in the environment and does not pick up noise from other directions. It is convenient as it allows efficient transmission with low power. Radio waves radiating in a specific direction are called a beam. Non-directional antennas radiate unwanted radio waves in the environment, and conversely pick up noise from every direction. However, communication is possible wherever the other party in communication goes, so they are suited to mobile applications. Directional antennas include Yagi-Uda arrays, parabola antennas and the like. Non-directional antennas include whip antennas and so on. The following diagrams show directivity. Although it is not shown here, naturally radio waves radiate in three dimensions, so we should also consider the directivity pattern when seen from the side too. The directional pattern diagrams show the relative intensity of the maximum field strength in any direction, thus indicating electric field directivity.

Directional antennas and non-directional antennas
In the diagram above, with the whip antenna the radio waves are radiating in every direction equally, so it is a non-directional antenna. With the Yagi-Uda array and parabola antenna, the radio waves are radiating in a specific direction, so they are said to be directional antennas (beam antennas)
In the diagram above, with the whip antenna the radio waves are radiating in every direction equally, so it is a non-directional antenna. With the Yagi-Uda array and parabola antenna, the radio waves are radiating in a specific direction, so they are said to be directional antennas (beam antennas)
Main lobe, side lobe, and back lobe
If we take the Yagi-Uda array as an example, the largest radiation beam in the intended direction is the main lobe, and in the opposite direction the unwanted radiation that occurs is called the side lobe. A side lobe occurring in space in the direction opposite to the main lobe is called back lobe.
If we take the Yagi-Uda array as an example, the largest radiation beam in the intended direction is the main lobe, and in the opposite direction the unwanted radiation that occurs is called the side lobe. A side lobe occurring in space in the direction opposite to the main lobe is called back lobe.
FB ratio
If we look at the directional pattern of the Yagi-Uda array, there are a main lobe and a back lobe generated. The ratio between the main lobe and back lobe, called the FB (Front/Back) ratio, is calculated to express the level of directivity of the antenna, and this is shown in decibels (dB). Therefore the larger this value, the better the performance of the antenna.

As the directional pattern diagram shows the field strength, we use 20 1og for the calculation.
If we look at the directional pattern of the Yagi-Uda array, there are a main lobe and a back lobe generated. The ratio between the main lobe and back lobe, called the FB (Front/Back) ratio, is calculated to express the level of directivity of the antenna, and this is shown in decibels (dB). Therefore the larger this value, the better the performance of the antenna.
As the directional pattern diagram shows the field strength, we use 20 1og for the calculation.
Gain of antennas

When choosing an antenna, directivity and gain are concerns. Furthermore, depending on the specification, the unit of gain is expressed variously as dBd, dB, dBi and it is difficult to make a decision on which to choose.
Also, because the antenna is made of metal and there is no circuit for electrical amplification, the fact that there is gain may seem a little strange.
Antennas can concentrate input energy in a certain direction, but there are differences in the method of concentration according to the type and between different antennas. In other words, antennas that spread the input power in directions other than that of the other party in communication, and antennas with directivity that concentrate the power efficiently, show differences in range. This difference is the difference of gain, and the higher the gain, the more acute directivity becomes, and this means that directional alignment becomes more difficult.
Antenna gain is expressed as he ratio of received power at the maximum electric field direction when the same power is input to an antenna under test and a reference antenna
To express antenna gain, there are two methods, one using an isotropic antenna as reference, the other using another type of antenna (usually a λ/2 half wave length dipole antenna) as reference.
When using an isotropic antenna as reference, the gain is called absolute gain, and the unit used is dBi.
When using an ideal half wave length (λ/2) dipole antenna as reference, the gain is called relative gain, and the unit used is dBd.
Also, because the antenna is made of metal and there is no circuit for electrical amplification, the fact that there is gain may seem a little strange.
Antennas can concentrate input energy in a certain direction, but there are differences in the method of concentration according to the type and between different antennas. In other words, antennas that spread the input power in directions other than that of the other party in communication, and antennas with directivity that concentrate the power efficiently, show differences in range. This difference is the difference of gain, and the higher the gain, the more acute directivity becomes, and this means that directional alignment becomes more difficult.
Antenna gain is expressed as he ratio of received power at the maximum electric field direction when the same power is input to an antenna under test and a reference antenna
To express antenna gain, there are two methods, one using an isotropic antenna as reference, the other using another type of antenna (usually a λ/2 half wave length dipole antenna) as reference.
When using an isotropic antenna as reference, the gain is called absolute gain, and the unit used is dBi.
When using an ideal half wave length (λ/2) dipole antenna as reference, the gain is called relative gain, and the unit used is dBd.
With relative gain, the ratio of the absolute gain of the antenna used as reference, and the absolute gain of the antenna in question is equivalent. As the absolute gain of the half wave length (λ/2) dipole antenna used as reference is 2.14 dBi, the relative gain Gr dBd of an antenna with absolute gain of Ga dBi is found by relative gain Gr dBd = absolute gain Ga dBi – 2.14 dB.
In other words, between dBd and dBi, the relationship 0 dBd = 2.14 dBi obtains.
If an antenna specification is 2.14 dBi, it means that it is equivalent to an ideal half wave length dipole antenna.
For antenna gain, the expressions dBd and dB mean the same thing, with dBd being the formal designation.
Isotropic antennas are theoretic, formulaic, virtual antennas, that radiate radio waves in all directions with equal intensity, and that have spherical directivity.
In other words, between dBd and dBi, the relationship 0 dBd = 2.14 dBi obtains.
If an antenna specification is 2.14 dBi, it means that it is equivalent to an ideal half wave length dipole antenna.
For antenna gain, the expressions dBd and dB mean the same thing, with dBd being the formal designation.
Isotropic antennas are theoretic, formulaic, virtual antennas, that radiate radio waves in all directions with equal intensity, and that have spherical directivity.
Impedance matching

When connecting an antenna from a high frequency circuit it is necessary to transfer power efficiently and ensure that no problems arise with reflection of the radio waves. Reflection occurs when the signal source impedance and the impedance of the antenna do not match, and making them match is called impedance matching. Reflection means the situation in which part of the signal sent in the direction of the antenna returns towards the signal source, and if it combines with the incident signal, adverse effects may arise.
The specification of an antenna will always include ″Input impedance: 50 Ω or the like, so impedance matching should be implemented at the connection circuit so as to match this value. It is also necessary for the impedance of the cable used to match. The impedance of the cable is decided by the per unit impedance and capacitance, and the impedance of cables on the market will always be indicated.
There are various methods of impedance matching. However, as it is a very involved subject, we would refer you to a specialist textbook.
The specification of an antenna will always include ″Input impedance: 50 Ω or the like, so impedance matching should be implemented at the connection circuit so as to match this value. It is also necessary for the impedance of the cable used to match. The impedance of the cable is decided by the per unit impedance and capacitance, and the impedance of cables on the market will always be indicated.
There are various methods of impedance matching. However, as it is a very involved subject, we would refer you to a specialist textbook.
Horizontally polarized waves and vertically polarized waves

The radio waves radiated from antennas standing vertically propagate vertically in relation to the ground, and are called vertical waves. In the same way, with horizontally placed antennas the electric field is horizontal in relation to the ground, so the waves are called horizontal waves. Circularly polarized waves are also used, for satellite broadcasts and so on.
Naturally, if the plane of polarization of both antennas does not match, there will be a lot of loss in capturing the radio waves.
Naturally, if the plane of polarization of both antennas does not match, there will be a lot of loss in capturing the radio waves.

Antenna material

Because high frequency currents flow through antennas, naturally they must be made of metal. Therefore, metals with a low specific resistance are used as the material for antennas. However, silver and gold are not appropriate from the perspective of cost accounting, and steel rusts and is heavy so it is not suitable for antennas. Ordinarily, aluminum is used for antennas for its low specific resistance and low cost, but this is often used for relatively large antennas. For compact equipment such as mobile phones and radio modules, antennas made of shape memory alloys (titanium-nickel alloy) or of stainless steel are used, or dielectric antennas. Even simple antennas made of piano wire are used.
How to use antennas

Antennas should be attached to the outside of the product, on the top if possible. The antenna should be attached in a position as far as possible from the human body. Radio waves above 750 MHz are particularly easily absorbed by the human body, so caution is required. For equipment that fits against the human body, allowance should be made for a distance of at least 2 to 3 cm. The case in which the radio module is incorporated should be ABS plastic. When using a metal case that attenuates radio waves, only the main unit of the radio module should be built in, and the antenna should be outside. Furthermore, you should ensure that the case of the module and the metal case have the same electric potential. The antenna should be kept as straight as possible and should not be bent into a circle. Make the plane of polarization of the radio waves match for both antennas. If the antenna is located externally, always use coaxial cable, and implement impedance matching.
Mobile phone antennas

When the antenna used in a mobile phone is extended, it is a λ/4 whip (rod) antenna, but when it is retracted, the coil in the tip becomes a helical antenna. Compared with the whip antenna, the sensitivity of this helical antenna is inferior, so mobile phones are used with the antenna extended. A receive only F type antenna is built into the inside of the phone, and the internal and external antennas receive using spatial diversity, and internal functions for power control and so on are applied to the signal. As this is a mobile application, directivity is non-directional. The frequency of the radio waves used in mobile phones (in Japan), is 800 MHz outgoing and 900 MHz incoming. If we calculate the length of the antenna (excluding the helical antenna) using the medial frequency of 850 MHz, the wave length λ with 850 MHz is
resulting in a λ/4 antenna of about 9 cm.
There are mobile phones that use the 800 MHz band, and those that use the 1,500 MHz band. The antenna of the latter is shorter. There are also mobile phones in the 800 MHz band with short antennas. There are also antennas in which, when extended, the upper helical antenna is electrically connected, becoming a λ/2 wave length antenna.
How to use mobile phones efficiently
For the reasons above, the following are suggestions for how to use a mobile phone without experiencing problems, and for high quality voice and data transmission.
Extend the antenna fully when using the phone, and take care not to cover it in any way. · As there is an internal antenna near the top of the phone, hold the phone near the bottom. · Try to keep the antenna as far from your body as possible. · If the state of the signal seems bad, trying moving or turning around. · Use an antenna of an appropriate length. Do not modify or replace the antenna. · Do not use a metal strap or metal fittings. · Make sure the antenna is vertical.
Emission units

If you look at the specification sheet for a radio module, or if the document is related to the Wireless Telegraphy Act, you will see a variety of units. Here we will explain about the basic units.
dB decibels

In electrical related fields, units using dB appear frequently, being used to indicate a relative ratio. dB indicates a relationship with a reference, such as 'larger dB than something' or 'smaller dB than something'. (There is also a unit dB that is used to measure sound pressure.)
To explain using the amplification factor of an amplifier's voltage amplification circuit as an example, if a signal of 1 mV is input into a circuit with a voltage gain of 10,000 times, an output voltage of 10,000 mV (10 V) will result. In this case, an electrical engineer would say that the circuit had a voltage gain of 80 dB rather than saying that it had a voltage gain of 10,000 times. There are the following reasons for this.
* From a visual point of view, 10,000 has 3 more zeroes that 80, and with larger values, the numbers can become unwieldy. By using dB, the value can be expressed with a smaller number of digits, making dB more convenient. If we assume that 1,234,567 times is 1.23 million times, expressed as dB it becomes 121.8 dB (1,230,268 times), and there is no particular inconvenience with using it for practical purposes.
* If, for example, we connect amplifiers with voltage gain of 50.11 times (34 dB) and 89.12 times (39 dB), the voltage gain is 50.11 times×89.12 times = 4,466 times, requiring complicated multiplication. However, if we express it in decibels, we have 34 dB + 39 dB = 73 dB (4,466 times), making it possible to calculate using addition or subtraction. If an attenuator or the like is introduced, we would have to use division, but with dB, it can be done using subtraction.
* 2 times, 3 times, 4 times, and 10 times each become 6 dB, 9.5 dB, 12 dB, and 20 dB, while 997 times, 999 times, 1003 times and 1005 times can all be expressed by 60 dB, so it may be said that the decibel expression more closely matches the human perception of amplification.
Formula
Voltage ratio = 20 log 10 (V2/V1), voltage gain = 20 log 10 (output voltage/input voltage), attenuation = 20 log 10 (output voltage/input voltage), field strength = 20 log 10 (E2/E1), ordinary amplification = 20 log 10 (A/B) Power gain = 10 log 10 (output power/input power)
* Decibel units using the absolute level for power or voltage as a reference are dBm, dBV, dBμV and so on.
* When looking at units, it is necessary to pay attention to what the reference is. In particular, we must be careful where power gain is concerned.
* Units that express an absolute level like dBm and the like should not be added to or subtracted from each other. So 20 dBm + 20 dBm = 23 dBm. * Absolute gain and relative gain can be added to or subtracted from each other. So 20 dBm + 20 dB = 40 dBm. Here we calculated what we would get when 20 dBm is input into a 20 dB power amplifier, so we used 10 log for the calculation.
* A mixture of units is used, so we must pay careful attention. The same unit dBμ is used for noise voltage, field strength and so on, and while ordinarily dBm or dBk is used for power, it is also sometimes expressed as dBμ, so caution is required. Recently, noise voltage, field strength and so on are being expressed with units such as dBμV and dBμV/m.
To explain using the amplification factor of an amplifier's voltage amplification circuit as an example, if a signal of 1 mV is input into a circuit with a voltage gain of 10,000 times, an output voltage of 10,000 mV (10 V) will result. In this case, an electrical engineer would say that the circuit had a voltage gain of 80 dB rather than saying that it had a voltage gain of 10,000 times. There are the following reasons for this.
* From a visual point of view, 10,000 has 3 more zeroes that 80, and with larger values, the numbers can become unwieldy. By using dB, the value can be expressed with a smaller number of digits, making dB more convenient. If we assume that 1,234,567 times is 1.23 million times, expressed as dB it becomes 121.8 dB (1,230,268 times), and there is no particular inconvenience with using it for practical purposes.
* If, for example, we connect amplifiers with voltage gain of 50.11 times (34 dB) and 89.12 times (39 dB), the voltage gain is 50.11 times×89.12 times = 4,466 times, requiring complicated multiplication. However, if we express it in decibels, we have 34 dB + 39 dB = 73 dB (4,466 times), making it possible to calculate using addition or subtraction. If an attenuator or the like is introduced, we would have to use division, but with dB, it can be done using subtraction.
* 2 times, 3 times, 4 times, and 10 times each become 6 dB, 9.5 dB, 12 dB, and 20 dB, while 997 times, 999 times, 1003 times and 1005 times can all be expressed by 60 dB, so it may be said that the decibel expression more closely matches the human perception of amplification.
Formula
Voltage ratio = 20 log 10 (V2/V1), voltage gain = 20 log 10 (output voltage/input voltage), attenuation = 20 log 10 (output voltage/input voltage), field strength = 20 log 10 (E2/E1), ordinary amplification = 20 log 10 (A/B) Power gain = 10 log 10 (output power/input power)
* Decibel units using the absolute level for power or voltage as a reference are dBm, dBV, dBμV and so on.
* When looking at units, it is necessary to pay attention to what the reference is. In particular, we must be careful where power gain is concerned.
* Units that express an absolute level like dBm and the like should not be added to or subtracted from each other. So 20 dBm + 20 dBm = 23 dBm. * Absolute gain and relative gain can be added to or subtracted from each other. So 20 dBm + 20 dB = 40 dBm. Here we calculated what we would get when 20 dBm is input into a 20 dB power amplifier, so we used 10 log for the calculation.
* A mixture of units is used, so we must pay careful attention. The same unit dBμ is used for noise voltage, field strength and so on, and while ordinarily dBm or dBk is used for power, it is also sometimes expressed as dBμ, so caution is required. Recently, noise voltage, field strength and so on are being expressed with units such as dBμV and dBμV/m.
Radio related units

Here we will explain about some of the units used in relation to radio, and units expressed in decibels. The following table contains some values that are somewhat meaningless in terms of practical applications, but they simply show the position of commonly used units.

■O dBμ is used in all examples, so it is misleading.
■Used frequently. 0 dBmW is easy to understand, but for some reason is not used.
■Used frequently. 0 dBmW is easy to understand, but for some reason is not used.
| dBm | An expression in decibels for voltage ratio using 1 μV of voltage as reference, this is 0 dB. This gives * 1 mW = 0 dBm, 10 mW = 10 dBm, 100 mW = 20 dBm * 1 mW = 30 dBm, 1 μW = -30 dBm, 1 nW = -60 dBm If we reverse this calculation we get  Digression: The 'm' in dBm indicates the prefix 'milli', so is the correct way of saying dBm "dee bee milli"? Also, why don't we say "dee bee milliwatt"? You would have thought that it would be easier to understand if the way we say this unit tallied with the others... |
| dBμV | An expression in decibels for voltage ratio using 1 μV of voltage as reference, this is 0 dB. This gives * 1 μV = 0 dBμV, 500 μV = 54 dBμV, 1 mV = 60 dBμV, 10 mV = 80 dBμV, 1 V = 120 dBμV If we reverse this calculation we get  |
| dBμV/m | An expression in decibels for voltage ratio using 1 μV /m of field strength as reference, this is 0 dB. This gives Example: With 500 μVm 20log10 (500 μV/m / 1 μV/m) = 54 dBμV/m * 1 μV/m = 0 dBμV/m, 500 μV/m = 54 dBμV/m, 35 μmV = 31 dBμV/m If we reverse this calculation we get  |
| dBi, dBd | Expresses antenna gain * When using an isotropic antenna as reference, the gain is called absolute gain, and the unit used is dBi. * When using an ideal half wave length (λ/2) dipole antenna as reference, the gain is called relative gain, and the unit used is dBd. The following relationship obtains between dBi and dBd. dBd = 2.14 dBi |
| dB/m | Expresses the attenuation of cables and the like. 0.033 dB/m means that for 1 m there is attenuation of 0.033 dB, and for 100 m there is attenuation of 3.3 dB. |
| ppm | ppm is 1/1,000,000 (1×10-6). |
| bps | This is a unit that expresses bit rate, indicating the number of bits that can be sent in 1 second. At 4,800 bps, 4,800 bits (600 bytes) of data can be sent in 1 second. |
Voltage EMF and PD notation

PD is short for potential difference, and it indicates the voltage of load impedance in a terminated state. 50 Ω is generally used as load impedance for high frequencies.
EMF is short for electromotive force, and it indicates signal source voltage in a state with no load (open voltage). In voltage notation EMF and PD have the relationship EMF = 2 × PD, and in dB notation, EMF = PD + 6 dB.
Example:
When impedance is 50 Ω power of 0 dBm is 0 dBm = 113 dBμVEMF = 107 dBμVPD = 223.8 mV. 7 μVEMF = 3.5 μVPD = 16.9 dBμVEMF = 10.88 dBμVPD = -96.1dBm 4.47 μVEMF = 2.235 μVPD = 13.0 dBμVEMF = 6.98 dBμVPD = -100.0 dBm
For the voltage notation in this Design Guide, EMF is always specified, and if nothing is specified, PD voltage is indicated. Impedance is 50 Ω.
EMF is short for electromotive force, and it indicates signal source voltage in a state with no load (open voltage). In voltage notation EMF and PD have the relationship EMF = 2 × PD, and in dB notation, EMF = PD + 6 dB.
Example:
When impedance is 50 Ω power of 0 dBm is 0 dBm = 113 dBμVEMF = 107 dBμVPD = 223.8 mV. 7 μVEMF = 3.5 μVPD = 16.9 dBμVEMF = 10.88 dBμVPD = -96.1dBm 4.47 μVEMF = 2.235 μVPD = 13.0 dBμVEMF = 6.98 dBμVPD = -100.0 dBm
For the voltage notation in this Design Guide, EMF is always specified, and if nothing is specified, PD voltage is indicated. Impedance is 50 Ω.
Impedance

When handling units, it is necessary to consider those relating to impedance. For low frequencies there is 600 Ω impedance, and for high frequencies there is 50 Ω impedance. At the same impedance of 0 dBm, the terminal voltage differs as follows, so caution is required.
600 ohm: Terminal voltage a V = √(PR) = √(1 mW × 600) = 0.775 v
50 ohm: Terminal voltage a V = √(PR) = √(1 mW × 50) = 0.224 v
75 ohm: Terminal voltage a V = √(PR) = √(1 mW × 75) = 0.274 v
600 ohm: Terminal voltage a V = √(PR) = √(1 mW × 600) = 0.775 v
50 ohm: Terminal voltage a V = √(PR) = √(1 mW × 50) = 0.224 v
75 ohm: Terminal voltage a V = √(PR) = √(1 mW × 75) = 0.274 v
50 Ω voltage V to power dBm conversion
 we get
we get 
For a voltage value, load power of 50 ohms is sought, and if we perform dBm conversion (1 mW reference),

* 1 V = 13.01 dBm, 1 mV = -46.98 dBm, 10 μV = -86.98 dBm, 1 μV = -106.98 dBm
50 Ω power dBm to voltage V conversion
To find the terminal voltage corresponding to power expressed in decibels when impedance is R = 50 Ω, first, find the corresponding power value P [W] for the converted power P50 dBm, and then find the terminal voltage.



* 20 dBm = 2.23 V, 10 dBm = 0.707 V , 0 dBm = 224 mV, -20 dBM = 22.4 mV



* 20 dBm = 2.23 V, 10 dBm = 0.707 V , 0 dBm = 224 mV, -20 dBM = 22.4 mV
50 Ω power W to voltage V conversion
When converting power to voltage V50 V when the impedance is 50 Ω, with P [W], V [V], and R [Ω], we get the following.
 so the result can be found easily.
so the result can be found easily.
* 1 W = 7.07 V, 100 mW = 2.23 V, 10 mW = 0.707 V, 1 mW = 22.4 mV
 so the result can be found easily.
so the result can be found easily.* 1 W = 7.07 V, 100 mW = 2.23 V, 10 mW = 0.707 V, 1 mW = 22.4 mV
Reading specifications

Here we explain about the main items in a specification for a radio module.
General characteristics

| Compatible specifications | These show the standard specifications to which the equipment conforms. |
| Channel span | This shows the frequency between each channel in the frequency band used and that is laid down in the standard specification. |
| Number of channels | This shows the number of channels used by the equipment in the frequency band used and that is laid down in the standard specification. |
| Data signal speed (bit rate) | This shows the speed at which the data signal itself is processed in radio transmissions and general transmissions. The unit is expressed as bits/second (bps). However fast the data signal speed in the specification is, time is taken when switching between sending and receiving and in processing the protocol, so actual data transmission speed will be slower. |
| Modulating speed (baud rate) | This shows the number of modulations within a unit of time, and the unit is a baud. Ordinarily called baud rate, it is sometimes confused with bit rate, but strictly speaking they are different. With multi-level modulation, although the baud rate is the same, the bit rate is different, and when data is transmitted in parallel, depending on the degree, the bit rate between transmitting and receiving is different. |
| Data transmission rate | This shows the mean data amount moving between transmitter and receiver within a unit of time, and the unit is expressed as bits/second, characters/second, characters/minute and so on. With actual transmissions, control data such as error control, equipment identification and the like is attached to the data, and if data errors occur, retransmission processing and so on is carried out. For these reasons, the data transmission rate is naturally slower in comparison with the data signal speed. |
| Emission class | This is shown as F1D, F2D, G1D and so on. They are a combination of symbols that correspond to various classifications such as the type of modulation of the main carrier, the qualities of the signal that modulates the main carrier, and the type of transmission information. F at the start means frequency modulation and G means phase modulation, while the next number 1 indicates digital signal, single channel equipment that does not use a sub-carrier for modulation. D at the end means 'data transmission, telemetry, and remote control'. |
| Communication method | There are two communication methods, two-way and one-way, and two kinds of two-way communication, half duplex operation and duplex operation. |
| Transmission output | This is the radio output of a transmitter. Each country has its own limit, so caution is necessary. |
| Range | Manufacturers present the results of tests performed in places where line of sight is possible, but the range differs considerable according to the environment of use, so this should only be taken as a rough guide. It differs according to buildings, people, vehicles and the topology of the vicinity, as well as in rain and snow. It is also affected by humidity from the ground. In addition, under similar conditions, if the wave length of the frequency used is shorter, naturally the range will be shorter too. |
Transmitting equipment characteristics

| Antenna power | The allowable output differs according to the frequency channel used, however in the 434 MHz band there are limits of less than 1 mW and less than 10 mW, and in the 868 MHz band, limits are divided into sub-parts of less than 5 mW, 10 mW, 25 mW, and 500 mW. | ||||||||||||
| Frequency error | The frequency error of the transmitter is the difference between the measured unmodulated carrier frequency and the nominal frequency as stated by the manufacturer. The standard values are different for fixed stations, mobile stations, and portable stations. | ||||||||||||
| Adjacent channel power | For devices with specified channel bandwidth, the adjacent channel power is that part of the total power output of a transmitter under defined conditions of modulation which falls within a specified passband centered on the nominal frequency of either of the adjacent channels. The regulation value differs with different frequencies and different channel separation. With EN300220, the regulation is as follows for 25 kHz steps.
| ||||||||||||
| Power of spurious emissions | Spurious emissions are unwanted emissions that fall outside the radio wave of interest, and this tolerance is laid down in the standard specification. With EN300220 they are regulated as follows.
|
Receiving equipment characteristics

| Receive sensitivity | This shows the received signal level when SINAD is 12 dB. This is sometimes expressed as power and sometimes as voltage. |
| Spurious emissions | Spurious radiations from the receiver are components at any frequency, radiated by the equipment and antenna. With EN300220, the regulation is 2 nW (less than 1,000 MHz) and 20 nW (more than 1,000 MHz). |
| Frequency error | The frequency error of the receiver is the difference between the measured local oscillation frequency and the nominal frequency as stated by the manufacturer. |
Modulation and demodulation

We will consider modulation and demodulation using an example in which a person's voice is sent.
If you talk to a person who is several kilometers away, the content (information) will not reach the other party however loud you speak. In this case we might consider transmission media such as radio waves, wires, light and the like, but voice itself vibrates the air with sound waves so sending that alone will not work. In this case, it is possible to change the sound to an electric signal using a microphone and send that signal. The electrical signal is a continuous (analog) representation of the proportional strength of the sound. The following two methods are available for transmitting the signal using radio waves or wire.
1 Sending the analog quantity as it is
2 Numerically converting the signal (digitizing it) and sending it as a digital quantity.
FM and AM radio use the first method, while mobile phones and BS digital broadcasting use the second method. At the receiving end, if the signal received is digital, it is converted into an analog quantity or voltage, and uses a speaker to produce sounds based on the strength of the voltage.
Let's consider sending radio wave data
Analog or digital information signals (called base band data) cannot simply be sent as they are through space. It is necessary to combine the base band data with a carrier frequency that is sufficiently high to pass through space as a radio wave. Converting the electric signal including the original information into a signal that is appropriate to the transmission path (in this case radio waves) in this way is called modulation. So modulation systems comprise analog modulation and digital modulation.
1 Analog modulation systems
Analog modulation systems include AM, FM, PM and so on. They modulate the carrier using an analog method.
2 Digital modulation systems
How is data that is originally a numerical value transmitted? There is apparently no other method of sending it than as a digital quantity (signal). Digital modulation directly shifts the high frequency parameters of the radio equipment using the base band data (digital quantity). There are may kinds of digital modulation systems such as FSK, MSK, CPFSK, GMSK, GFSK, ASK, PSK, DBPSK, DQPSK, QPSK, BPSK, multi-value QAM, OFDM, CCK and so on.
If you talk to a person who is several kilometers away, the content (information) will not reach the other party however loud you speak. In this case we might consider transmission media such as radio waves, wires, light and the like, but voice itself vibrates the air with sound waves so sending that alone will not work. In this case, it is possible to change the sound to an electric signal using a microphone and send that signal. The electrical signal is a continuous (analog) representation of the proportional strength of the sound. The following two methods are available for transmitting the signal using radio waves or wire.
1 Sending the analog quantity as it is
2 Numerically converting the signal (digitizing it) and sending it as a digital quantity.
FM and AM radio use the first method, while mobile phones and BS digital broadcasting use the second method. At the receiving end, if the signal received is digital, it is converted into an analog quantity or voltage, and uses a speaker to produce sounds based on the strength of the voltage.
Let's consider sending radio wave data
Analog or digital information signals (called base band data) cannot simply be sent as they are through space. It is necessary to combine the base band data with a carrier frequency that is sufficiently high to pass through space as a radio wave. Converting the electric signal including the original information into a signal that is appropriate to the transmission path (in this case radio waves) in this way is called modulation. So modulation systems comprise analog modulation and digital modulation.
1 Analog modulation systems
Analog modulation systems include AM, FM, PM and so on. They modulate the carrier using an analog method.
2 Digital modulation systems
How is data that is originally a numerical value transmitted? There is apparently no other method of sending it than as a digital quantity (signal). Digital modulation directly shifts the high frequency parameters of the radio equipment using the base band data (digital quantity). There are may kinds of digital modulation systems such as FSK, MSK, CPFSK, GMSK, GFSK, ASK, PSK, DBPSK, DQPSK, QPSK, BPSK, multi-value QAM, OFDM, CCK and so on.
Frequency shift modulation

Frequency shift modulation includes the following systems, and all of these types are related.
| FSK | Frequency Shift Keying |
| CPFSK | Continuous Phase Frequency Shift Keying |
| MSK | Minimum Shift Keying |
| GMSK | Gaussian filtered MSK |
The FSK system is a modulation system in which the logic of the digital code making up the base band data is shifted proportionally in the frequency of the carrier. The carrier is switched between different frequencies when the logic is 1 and when the logic is 0. There are systems in which the phase of the modulated wave is continuous, and others in which it is not. Those systems with continuous phases are called CPFSK, which is the most often used of the FSK systems. In addition, in order to increase bandwidth utilization efficiency, the modulation index m is set to 0.5, and with a narrower frequency band, the system is called MSK (Minimum Shift Keying). GMSK (Gaussian filtered MSK) has an even narrower band than the MSK system.
In order to generate a frequency in accordance with the logical value of the base band data, the CPFSK system uses a VCO (Voltage Controlled Oscillator). The VCO changes the oscillating frequency according to the level of the digital data of the base band that is applied to its circuit, so that the phase is continuous. Among FSK systems, those that use two oscillators and do not use continuous phase are not used much as they result in a wider frequency band.
The circuit systems of FSK systems (CPFSK) themselves are simple, but as the frequency bandwidth used (occupied frequency bandwidth) is wide compared with PSK systems and the like, in order to keep bandwidth as small as possible without losing the characteristics of the CPFSK system, the MSK system and GMSK system with their narrower frequency band are also used. The occupied frequency bandwidth (the extent of the spread of the spectrum) of FSK systems is decided by the modulation index expressed by the frequency spectrum of the base band data and the depth of the modulation.
If modulation index is m, frequency shift is Δf (one side), and the time length of 1 bit of data if T,
m = 2 × Δf × T = 2 × Δf/bit rate resulting in Δf = m × bit rate/2
* bit rate = 1/T Unit: bits/second (bps)
It can be seen that with a similar bit rate, the larger the modulation index, the greater the occupied bandwidth will be. With FSK, the higher the modulation index, the higher the SN (signal to noise ratio) in the demodulation at the receiver, but the occupied bandwidth increases and bandwidth utilization efficiency falls. The MSK system is the same as the CPFSK system but with a modulation index of 0.5.
Furthermore, with the GMSK system a Gaussian filter is applied to the base band data input in the VCO, making the occupied frequency bandwidth narrower.
Binary FSK
In the specification for radio equipment and radio modules, you may sometimes see the term binary FSK. This refers to normal FSK (MSK, CPFSK and so on) in which two frequencies are assigned to the data logic, and 1 bit is sent with 1 modulation. Quadruple conversion FSK sends 2 bits with 1 modulation, so that the bit rate is doubled.
Direct FSK
This expression is used when making a distinction from analog modulation systems to stress that it is digital modulation.
In order to generate a frequency in accordance with the logical value of the base band data, the CPFSK system uses a VCO (Voltage Controlled Oscillator). The VCO changes the oscillating frequency according to the level of the digital data of the base band that is applied to its circuit, so that the phase is continuous. Among FSK systems, those that use two oscillators and do not use continuous phase are not used much as they result in a wider frequency band.
The circuit systems of FSK systems (CPFSK) themselves are simple, but as the frequency bandwidth used (occupied frequency bandwidth) is wide compared with PSK systems and the like, in order to keep bandwidth as small as possible without losing the characteristics of the CPFSK system, the MSK system and GMSK system with their narrower frequency band are also used. The occupied frequency bandwidth (the extent of the spread of the spectrum) of FSK systems is decided by the modulation index expressed by the frequency spectrum of the base band data and the depth of the modulation.
If modulation index is m, frequency shift is Δf (one side), and the time length of 1 bit of data if T,
m = 2 × Δf × T = 2 × Δf/bit rate resulting in Δf = m × bit rate/2
* bit rate = 1/T Unit: bits/second (bps)
It can be seen that with a similar bit rate, the larger the modulation index, the greater the occupied bandwidth will be. With FSK, the higher the modulation index, the higher the SN (signal to noise ratio) in the demodulation at the receiver, but the occupied bandwidth increases and bandwidth utilization efficiency falls. The MSK system is the same as the CPFSK system but with a modulation index of 0.5.
Furthermore, with the GMSK system a Gaussian filter is applied to the base band data input in the VCO, making the occupied frequency bandwidth narrower.
Binary FSK
In the specification for radio equipment and radio modules, you may sometimes see the term binary FSK. This refers to normal FSK (MSK, CPFSK and so on) in which two frequencies are assigned to the data logic, and 1 bit is sent with 1 modulation. Quadruple conversion FSK sends 2 bits with 1 modulation, so that the bit rate is doubled.
Direct FSK
This expression is used when making a distinction from analog modulation systems to stress that it is digital modulation.
Phase shift keying

Phase shift modulation includes the following systems.
| PSK | Phase Shift Keying |
| BPSK | Binary Phase Shift Keying |
| QPSK | Quadurature Phase Shift Keying |
| DBPSK | Differential Binary Phase Shift Keying |
| DQPSK | Differential Quadurature Phase Sift Keying |
The PSK modulation system is a modulation system that changes the phase of the carrier by proportionally shifting the code of the base band data. Power and frequency efficiency is very good compared with ASK and FSK, and PSK is characterized by having a low rate of data errors. In addition, multi-level modulation is easily performed, while compared with FSK, the occupied frequency bandwidth is beneficially narrow so that it is actually used in many applications. However, as the processing circuits can be complex and phase characteristics are not linear, then data errors will occur requiring an engineering solution. This applies to all members of the PSK system family.
The PSK modulation system includes differential phase modulation (DBPSK, DQPSK) and absolute phase modulation (BPSK, QPSK). Differential phase encoding is normally used for its reliable demodulation. Of the differential phase encoding systems, with DBPSK if the data is 1, it causes the outgoing carrier to undergo an 180-degree phase shift, and if it is 0, it does nothing.
The DQPSK system shifts the phase of the carrier in 90 degree increments; phases are allocated to blocks of 2 bits in the received data stream, and phase shifting is applied to the phases of the outgoing carrier. The DQPSK system occupies the same bandwidth as the DBPSK system, but it can send twice the information (it has double the bit rate) so it is used frequently in applications.
The PSK modulation system includes differential phase modulation (DBPSK, DQPSK) and absolute phase modulation (BPSK, QPSK). Differential phase encoding is normally used for its reliable demodulation. Of the differential phase encoding systems, with DBPSK if the data is 1, it causes the outgoing carrier to undergo an 180-degree phase shift, and if it is 0, it does nothing.
The DQPSK system shifts the phase of the carrier in 90 degree increments; phases are allocated to blocks of 2 bits in the received data stream, and phase shifting is applied to the phases of the outgoing carrier. The DQPSK system occupies the same bandwidth as the DBPSK system, but it can send twice the information (it has double the bit rate) so it is used frequently in applications.
Amplitude shift keying

| ASK (amplitude shift keying) | A modulation system in which the amplitude of the carrier is shifted proportionally to the base band data. ASK is susceptible to noise and interference, so it is not used much for data transmissions over long distances. However it is a simple and compact system and is cheap to implement, so it is used by micro-power radio operators and the like for short range communications. The oscillation circuit does not stop when the data bit is either 1 or 0, which differentiates ASK from OOK. |
| OOK (On - Off keying) | Similarly to ASK, OOK turns a carrier of constant frequency and constant amplitude on and off, but when it is off, the oscillation circuit stops completely. For this reason modules using OOK can achieve low power consumption. |
Waves

Addition and multiplication of waves

Although 'mixer' is a commonly used word, the output results of mixers used for audio circuits and those used for radio circuits are very different. When mixing two signals with an audio circuit mixer, the levels of the input signals are combined (added), whereas with a radio circuit mixer, the frequencies are added and subtracted (multiplied). With an audio circuit mixer, the frequencies of the input signals are not changed but with a radio circuit mixer, the frequencies are converted.
Addition of waves
The red line is the waveform when two sine waves are added. In this addition, the levels are added together. The output of audio mixers corresponds to this result.
Addition of waves
The red line is the waveform when two sine waves are added. In this addition, the levels are added together. The output of audio mixers corresponds to this result.
Multiplication of waves
The red line in the middle is the result of multiplication of sine waves f1 and f2 by a mixer. As a result of this multiplication, f1 + f2 and f1 - f2 signals occur, so if it is necessary for the circuit, extract the signal with a bandpass filter. The radio equipment extracts the sum component with up-conversion and the difference component with down-conversion. From the point of view of hardware, the multiplication of a mixer uses the higher harmonics that are generated by the non-linear part that powers a semiconductor.
The red line in the middle is the result of multiplication of sine waves f1 and f2 by a mixer. As a result of this multiplication, f1 + f2 and f1 - f2 signals occur, so if it is necessary for the circuit, extract the signal with a bandpass filter. The radio equipment extracts the sum component with up-conversion and the difference component with down-conversion. From the point of view of hardware, the multiplication of a mixer uses the higher harmonics that are generated by the non-linear part that powers a semiconductor.
Addition of waves that have phase differences
The red line is the calculation result. If the radio waves have been reflected off a body, a phase difference occurs between the direct waves so that the level of the composite signal fluctuates between strong and weak. The fading, in accordance with the multipaths taken through space and the reflection phenomenon that arises inside the antenna, corresponds to this phenomenon.
The red line is the calculation result. If the radio waves have been reflected off a body, a phase difference occurs between the direct waves so that the level of the composite signal fluctuates between strong and weak. The fading, in accordance with the multipaths taken through space and the reflection phenomenon that arises inside the antenna, corresponds to this phenomenon.
Multiplication of waves that have phase differences
The red line is the mid component of the result of multiplication by a mixer of similar frequencies that have phase differences. A frequency multiplier is used.
The red line is the mid component of the result of multiplication by a mixer of similar frequencies that have phase differences. A frequency multiplier is used.
Frequency conversion of CPFSK

The next applet shows up-conversion of a CPFSK waveform. f1 is a carrier, and f2 is a CPFSK signal generated by inputting a base band signal in a VCO. The red line in the middle is the result of multiplication of f1 and f2, but this waveform also includes f1 + f2 and f1 - f2 and other harmonics. (For example, the frequency of the modulated waves of Circuit Design's MU-1 have a carrier frequency of 1/20 (400 MHz band) ~ 1/60 (1,200 MHz band).) As a result of this multiplication, f1 + f2 and f1 - f2 signals occur, so the f1 + f2 signal is extracted with a bandpass filter by the transmitter. Similarly at the receiver, down-conversion is performed by a mixer to extract the difference signal.
Resolving the waves

You may have heard that any waveform is made up of several sine waves with different frequencies and levels. With this applet, 5 sine waves with different phases and levels can be added as a means of practical demonstration.
Click the Square wave, Triangular wave, and Sawtooth wave buttons to set the phase and level of the higher harmonics, and the respective waveforms are shown. When the start phase is combined with an odd-order higher harmonic, the result is a square wave like the red line. You can see the relationship between fundamental harmonics and higher harmonics.
If the signal is passed through a filter circuit with poor performance, a phase lag in the harmonics that form the signal may occur and the output signal will be changed. The tops of the square wave and sawtooth wave are undulating, but when combined with further components such as 11th order or 13th order waves, it comes closer to an actual waveform.
Click the Square wave, Triangular wave, and Sawtooth wave buttons to set the phase and level of the higher harmonics, and the respective waveforms are shown. When the start phase is combined with an odd-order higher harmonic, the result is a square wave like the red line. You can see the relationship between fundamental harmonics and higher harmonics.
If the signal is passed through a filter circuit with poor performance, a phase lag in the harmonics that form the signal may occur and the output signal will be changed. The tops of the square wave and sawtooth wave are undulating, but when combined with further components such as 11th order or 13th order waves, it comes closer to an actual waveform.
Is it OK to use any frequency?

Each country and region decides which frequencies can be used and with which applications. The 2.4 GHz frequency band is used in Europe, America and Japan as the ISM band, but 434 MHz and 868 MHz are only used in Europe. Furthermore, 426 MHz, 429 MHz, and 1,200 MHz are assigned in Japan to telemetry, telecontrol and data transmission, but they cannot be used in other countries.
What is the range?

Users will be concerned to know the operating range of the equipment, and this is an important issue for equipment manufacturers as well.
You may want to suggest a long operating range in the specification, but it is no good if the user comes to view this specification with suspicion when actually using the equipment. Therefore it is necessary to include a disclaimer such as "Communication range varies according to the environment of use." The range shown in the specification of the radio module itself is only a guide, and when choosing a radio module it is necessary to test it using an actual evaluation board.
Receive sensitivity
The difference in communication range within the limits of the stipulated output indicates the good and bad points of the performance of the module. Communication range varies according to a number of conditions so sometimes it may not be included in the specification, however receive sensitivity is always included so we will compare the two.
Difference due to frequency
Communication range differs according to the frequency used. The higher the frequency of the radio wave, the higher its straightness and the less far it travels. 400 MHz radio waves are subject to the diffraction phenomenon and travel further than straighter 2.4 GHz radio waves.
Difference due to modulation system
ASK is more affected by background noise than FSK or PSK, and even if the radio wave reaches the receiver, data errors may occur.
Increasing the operating range
Using a gain antenna
With receive only equipment, you can choose any kind of antenna. You can expect to increase the range if you use a gain antenna with good performance. Please conduct field testing with a number of antennas before selecting one. The integral and dedicated antennas used in CE approved radio modules are calibrated for transmission output in conformity with the specification, and should not be replaced for trivial reasons.
Careful design
When using a radio module, it is important that your design does not in any way degrade the receive sensitivity that is shown in the specification. It is also important to make every effort to avoid errors. Please pay attention to the following points.
* Ensure that the radio module is not subject to noise from the CPU or other devices in the system in which it is incorporated.
* Reduce noise coming from the system's control switch and the like.
* Make the position of the receiver a place where there is a minimum of noise.
* Take care in attaching the antenna.
You may want to suggest a long operating range in the specification, but it is no good if the user comes to view this specification with suspicion when actually using the equipment. Therefore it is necessary to include a disclaimer such as "Communication range varies according to the environment of use." The range shown in the specification of the radio module itself is only a guide, and when choosing a radio module it is necessary to test it using an actual evaluation board.
Receive sensitivity
The difference in communication range within the limits of the stipulated output indicates the good and bad points of the performance of the module. Communication range varies according to a number of conditions so sometimes it may not be included in the specification, however receive sensitivity is always included so we will compare the two.
Difference due to frequency
Communication range differs according to the frequency used. The higher the frequency of the radio wave, the higher its straightness and the less far it travels. 400 MHz radio waves are subject to the diffraction phenomenon and travel further than straighter 2.4 GHz radio waves.
Difference due to modulation system
ASK is more affected by background noise than FSK or PSK, and even if the radio wave reaches the receiver, data errors may occur.
Increasing the operating range
Using a gain antenna
With receive only equipment, you can choose any kind of antenna. You can expect to increase the range if you use a gain antenna with good performance. Please conduct field testing with a number of antennas before selecting one. The integral and dedicated antennas used in CE approved radio modules are calibrated for transmission output in conformity with the specification, and should not be replaced for trivial reasons.
Careful design
When using a radio module, it is important that your design does not in any way degrade the receive sensitivity that is shown in the specification. It is also important to make every effort to avoid errors. Please pay attention to the following points.
* Ensure that the radio module is not subject to noise from the CPU or other devices in the system in which it is incorporated.
* Reduce noise coming from the system's control switch and the like.
* Make the position of the receiver a place where there is a minimum of noise.
* Take care in attaching the antenna.
Incorporating radio modules in other equipment

Measures against internal noise

The equipment in which radio modules are incorporated will often be equipped with high speed CPUs and logic circuits. These components emit high frequency noise in the form of harmonics with the rising edge and falling edge of the control signal, and these have adverse effects on the frequency band used. It is necessary to take measures to ensure that this noise is not allowed to impinge on the antenna of the receiver or transmitter. Next we will consider a list of points requiring caution when incorporating radio modules in other equipment. Please note that the following does not necessarily apply to all modules.
* The case in which the radio module is incorporated should be of a material that allows radio waves to pass through it, such as ABS plastic. The module cannot emit or capture radio waves inside a metal case. If a metal case is used, only the main unit of the radio module should be built in, and the antenna should be outside. The body of the module should make electrical contact with the metal case and there should be no electric potential difference. The same applies to cases with electric conductive coating
* The radio module and antenna should be kept separate from noise sources as far as possible.
* If the antenna of the transmitter or receiver does not match the plane of polarization of the radio wave, efficient communication cannot be achieved, communication range will be poor, and errors will occur.
* If the antenna of the transmitter is vertical, make the antenna of the receiver vertical too. Take the conditions of use into consideration when attaching the antenna.
* Do not allow the whip antenna of the module to be attached so that it is bent. Try to keep it as vertical as possible.
* If the module is built into equipment that includes a source of noise emissions, be sure to connect the antenna using coaxial cable. Antenna circuits that do not have impedance matching cause problems with reflection of the radio waves, and besides reducing efficiency, they cause adverse effects to the equipment.
* The CPU that controls the radio module and the signal lines from other logic are sources of noise and should therefore be kept as short as possible.
* Use a separate regulator for the power source of the radio module and keep it separate from the power sources of other noise emitting digital circuits. If this is not possible, take the power directly after that for the main unit power source, and apply RF decoupling. RF decoupling uses CR filters, LC filters, EMI filters and so on to cut the noise frequencies as necessary.
* If these power sources are included within the same case, ground them away from other circuits and separate them with shield plates and so on.
* When installing a radio module on the substrate of control circuit, try to make the ground of the control circuit as extensive as possible. Use the power line directly after that for the power circuit, and apply RF decoupling. In addition, in order to locate it as far as possible from noise sources, mount the module on the reverse side of the substrate from that with digital circuits mounted on it.
* Do not change the antenna if the module already has one. If you are designing a new antenna, use one with a length of λ/4.
* Check whether the clock frequency used by the CPU is an integer of 1 or thereabouts of the radio frequency used. The harmonics from this clock frequency will have an adverse effect on the radio circuit.
* The case in which the radio module is incorporated should be of a material that allows radio waves to pass through it, such as ABS plastic. The module cannot emit or capture radio waves inside a metal case. If a metal case is used, only the main unit of the radio module should be built in, and the antenna should be outside. The body of the module should make electrical contact with the metal case and there should be no electric potential difference. The same applies to cases with electric conductive coating
* The radio module and antenna should be kept separate from noise sources as far as possible.
* If the antenna of the transmitter or receiver does not match the plane of polarization of the radio wave, efficient communication cannot be achieved, communication range will be poor, and errors will occur.
* If the antenna of the transmitter is vertical, make the antenna of the receiver vertical too. Take the conditions of use into consideration when attaching the antenna.
* Do not allow the whip antenna of the module to be attached so that it is bent. Try to keep it as vertical as possible.
* If the module is built into equipment that includes a source of noise emissions, be sure to connect the antenna using coaxial cable. Antenna circuits that do not have impedance matching cause problems with reflection of the radio waves, and besides reducing efficiency, they cause adverse effects to the equipment.
* The CPU that controls the radio module and the signal lines from other logic are sources of noise and should therefore be kept as short as possible.
* Use a separate regulator for the power source of the radio module and keep it separate from the power sources of other noise emitting digital circuits. If this is not possible, take the power directly after that for the main unit power source, and apply RF decoupling. RF decoupling uses CR filters, LC filters, EMI filters and so on to cut the noise frequencies as necessary.
* If these power sources are included within the same case, ground them away from other circuits and separate them with shield plates and so on.
* When installing a radio module on the substrate of control circuit, try to make the ground of the control circuit as extensive as possible. Use the power line directly after that for the power circuit, and apply RF decoupling. In addition, in order to locate it as far as possible from noise sources, mount the module on the reverse side of the substrate from that with digital circuits mounted on it.
* Do not change the antenna if the module already has one. If you are designing a new antenna, use one with a length of λ/4.
* Check whether the clock frequency used by the CPU is an integer of 1 or thereabouts of the radio frequency used. The harmonics from this clock frequency will have an adverse effect on the radio circuit.

ISM band equipment

It is often said that there is a frequency band that is common worldwide as an ISM band, but in fact there are subtle differences to the standard in each country and careful investigation of this is required.
Take care not to sell modules or equipment that is in breach of the law.
Take care not to sell modules or equipment that is in breach of the law.
The original SMA design called for two compliant connectors:
SMA Female

RP-SMA Female

RP-SMA Male
The above two connectors were designed to be used together, but there was a problem with this configuration and the FCC started moving towards Part 15 compliance. All this means is that all the SMA RF connectors are changing gender (center pin). Really annoying for those of us who need to mate an antenna to an RF device. The FCC gender change was instituted to prevent home users from damaging RF equipment (think home WiFi) when screwing on an antenna. If all antennas are female, there is no way to damage the center connector.
There is one consistancy however; all antennas, cables or anything was being attached to a potential stationary object used an outer nut or inner thread design and all stationary devices used the outer thread design. This applies for all SparkFun products. All of our antennas are either SMA male or RP-SMA female. All of our boards are either SMA female or RP-SMA male.
The only thing that changed with the Part 15 compliance was the center pin, thus reversing the polarity of the connection and forming a “new” standard; the reversed polarized SMA (RP-SMA).
The next two photos are considered reversed polarized (RP-SMA).
There is one consistancy however; all antennas, cables or anything was being attached to a potential stationary object used an outer nut or inner thread design and all stationary devices used the outer thread design. This applies for all SparkFun products. All of our antennas are either SMA male or RP-SMA female. All of our boards are either SMA female or RP-SMA male.
The only thing that changed with the Part 15 compliance was the center pin, thus reversing the polarity of the connection and forming a “new” standard; the reversed polarized SMA (RP-SMA).
The next two photos are considered reversed polarized (RP-SMA).
RP-SMA Female
RP-SMA Male
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
MOVE ENERGY WITH SWITCH X <---> SWITCH O ........ LJBUSAF
Propagation switch X and switch O is a super wireless propagation ..... LJBUSAF
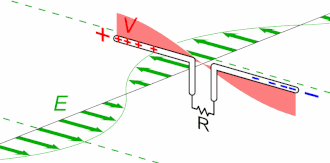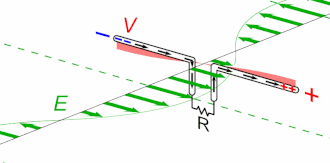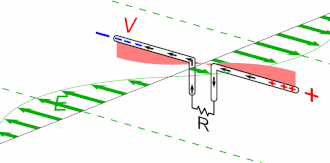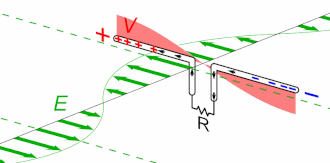















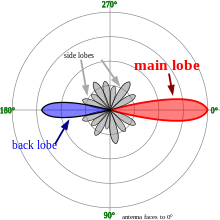

















































































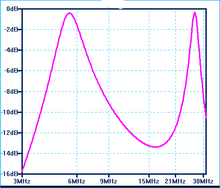


































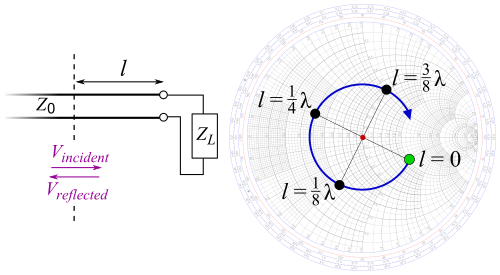
































![{\displaystyle \Gamma =c+jd=\left[{\frac {a^{2}+b^{2}-1}{(a+1)^{2}+b^{2}}}\right]+j\left[{\frac {2b}{(a+1)^{2}+b^{2}}}\right]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd10a31c990bc9c906a25d68963154624e37230d)
















































































































Thanks For sharing very helpful information
BalasHapusRF Admitance Level Switch Rod/Rope
https://jeepgrandcherokee-2018.blogspot.com/2020/07/jeep-cherokee-cb-antenna.html?showComment=1623417053484#c2415352202587807166
BalasHapus
BalasHapusRegardless of how wonderful your wonderful CB radio is,
it will not be of significant assistance if it doesn’t have a reliable CB antenna that it can go with.
So, if you need to bypass problems including loss of signal or noise as well as interruptions during communication,
then going for the best CB radio antenna is very important.
It’s possible to purchase a CB radio antenna via or from the stores across your street.
However, understanding its features is crucial. Rather than searching all through the internet,
jumping from one page to the other, this article has got you covered as following comprehensive research;
we have compiled a list of the top 5 best CB radio antennas. This way, you will easily get the best antenna with only a click of a button.
best small CB radio antenna
Great piece of information about Waveguide adapters
BalasHapus