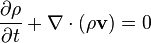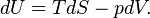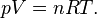Centrifugal compressor in probe for Jet Fighter ( CC ^ Pointer gun )

the theory of Centrifugal compressors, sometimes termed radial compressors, are a sub-class of dynamic axisymmetric work-absorbing turbomachinery.
The idealized compressive dynamic turbo-machine achieves a pressure rise by adding kinetic energy/velocity to a continuous flow of fluid through the rotor or impeller. This kinetic energy is then converted to an increase in potential energy/static pressure by slowing the flow through a diffuser. The pressure rise in impeller is in most cases almost equal to the rise in the diffuser section.




 

Theory of operation

 

Turbomachinery similarities

Centrifugal compressors are similar in many ways to other turbomachinery and are compared and contrasted as follows:

Similarities to axial compressor Centrifugal compressors are similar to axial compressors in that they are rotating airfoil based compressors as shown in the adjacent figure. It should not be surprising that the first part of the centrifugal impeller looks very similar to an axial compressor. This first part of the centrifugal impeller is also termed an inducer. Centrifugal compressors differ from axials as they use a greater change in radius from inlet to exit of the rotor/impeller.

Cutaway showing an axi-centrifugal compressor gas turbine

similarities to centrifugal fan Centrifugal compressors are also similar to centrifugal fans of the style shown in neighboring figure as they both increase the flows energy through increasing radius. In contrast to centrifugal fans, compressors operate at higher speeds to generate greater pressure rises. In many cases the engineering methods used to design a centrifugal fan are the same as those to design a centrifugal compressor. As a result, they can at times look very similar. This relationship is less true in comparison to a squirrel-cage fan as shown in figure farthest right. For purposes of generalization and definition, it can be said that centrifugal compressors often have density increases greater than 5 percent. Also, they often experience relative fluid velocities above Mach number 0.3 when the working fluid is air or nitrogen. In contrast, fans or blowers are often considered to have density increases of less than five percent and peak relative fluid velocities below Mach 0.3.

A low speed, low pressure centrifugal compressor or centrifugal fan, with upward discharging cone used to diffuse the air velocity

A squirrel-cage fan, without a discharge diffuser

Similarities to centrifugal pump Centrifugal compressors are also similar to centrifugal pumps[1] of the style shown in the adjacent figures. The key difference between such compressors and pumps is that the compressor working fluid is a gas (compressible) and the pump working fluid is liquid (incompressible). Again, the engineering methods used to design a centrifugal pump are the same as those to design a centrifugal compressor. Yet, there is one important difference: the need to deal with cavitation in pumps.

A 3D-solids model of a type of centrifugal pump

Cut-away of a centrifugal pump

Similarities to radial turbine Centrifugal compressors also look very similar to their turbomachinery counterpart the Radial_turbine as shown in the figure. While a compressor transfers energy into a flow to raise its pressure, a turbine operates in reverse, by extracting energy from a flow, thus reducing its pressure. In other words, power is input to compressors and output from turbines.

Cutaway showing a radial-inflow turbine that looks similar to the turbine shown .

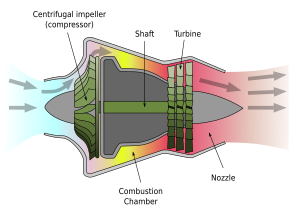
Turbo charger

Π theorem

The three independent dimensions used in this procedure for turbomachinery are:

• mass (force is an alternative)

• length

• time

According to the theorem each of the eight main parameters are equated to its independent dimensions as follows:

Flow:		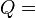	ex. = m^3/s
Head:		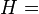	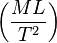ex. = kg*m/s^2
Speed:			ex. = m/s
Power:		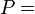	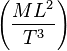ex. = kg*m^2/s^3
Density:			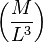ex. = kg/m^3
Viscosity:		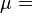	ex. = kg/(m*s)
Diameter:			ex. = m
Speed of sound:		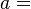	ex. = m/s

Classic turbomachinery similitude

Completing the task of following the formal procedure results in generating this classic set of five dimensionless parameters for turbomachinery. Full similitude is achieved when each of the 5 Pi-parameters are equivalent. This of course would mean the two turbomachines being compared are geometrically similar and running at the same operating point.

Flow coefficient: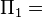
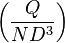Head coefficient: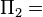
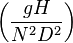Speed coefficient:
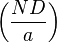Power coefficient: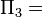
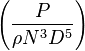Reynolds coefficient: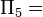

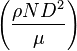Turbomachinery analysts gain tremendous insight into performance by comparisons of these 5 parameters with efficiencies and loss coefficients which are also dimensionless. In general application, the flow coefficient and head coefficient are considered of primary importance. Generally, for centrifugal compressors, the velocity coefficient is of secondary importance while the Reynolds coefficient is of tertiary importance. In contrast, as expected for pumps, the Reynolds number becomes of secondary importance and the velocity coefficient almost irrelevant. It may be found interesting that the speed coefficient may be chosen to define the y-axis, while at the same time the Reynolds coefficient may be chosen to define the z-axis.

Aero-thermodynamic fundamentals

The following equations outline a fully three-dimensional mathematical problem that is very difficult to solve even with simplifying assumptions. Until recently, limitations in computational power, forced these equations to be simplified to an Inviscid two-dimensional problem with pseudo losses. Before the advent of computers, these equations were almost always simplified to a one-dimensional problem.
Solving this one-dimensional problem is still valuable today and is often termed mean-line analysis. Even with all of this simplification it still requires large textbooks to outline and large computer programs to solve practically.

Conservation of mass

Also termed continuity, this fundamental equation written in general form is as follows:

Conservation of momentum

Also termed the Navier–Stokes equations, this fundamental is derivable from Newton's second law when applied to fluid motion. Written in compressible form for a Newtonian fluid, this equation may be written as follows:

Conservation of energy

The First Law of Thermodynamics is the statement of the conservation of energy. Under specific conditions, the operation of a Centrifugal compressor is considered a reversible process. For a reversible process, the total amount of heat added to a system can be expressed as where is temperature and is entropy. Therefore, for a reversible process:

Since U, S and V are thermodynamic functions of state, the above relation holds also for non-reversible changes. The above equation is known as the fundamental thermodynamic relation.

Equation of state

The classical ideal gas law may be written:

The ideal gas law may also be expressed as follows

where is the density, is the adiabatic index (ratio of specific heats), is the internal energy per unit mass (the "specific internal energy"), is the specific heat at constant volume, and is the specific heat at constant pressure.

With regard to the equation of state, it is important to remember that while air and nitrogen properties (near standard atmospheric conditions) are easily and accurately estimated by this simple relationship, there are many centrifugal compressor applications where the ideal relationship is inadequate. For example, centrifugal compressors used for large air conditioning systems (water chillers) use a refrigerant as a working gas that cannot be modeled as an ideal gas. Another example are centrifugal compressors design and built for the petroleum industry. Most of the hydrocarbon gases such as methane and ethylene are best modeled as a real gas equation of state rather than ideal gases.