A half spring O max spring not semi ring

Variable Force

( DElta )

Suppose F acting on a mass m depends on x; e.g., F = kx We divide x into little increments, Dxi, where Fi is the average force over that interval:

  

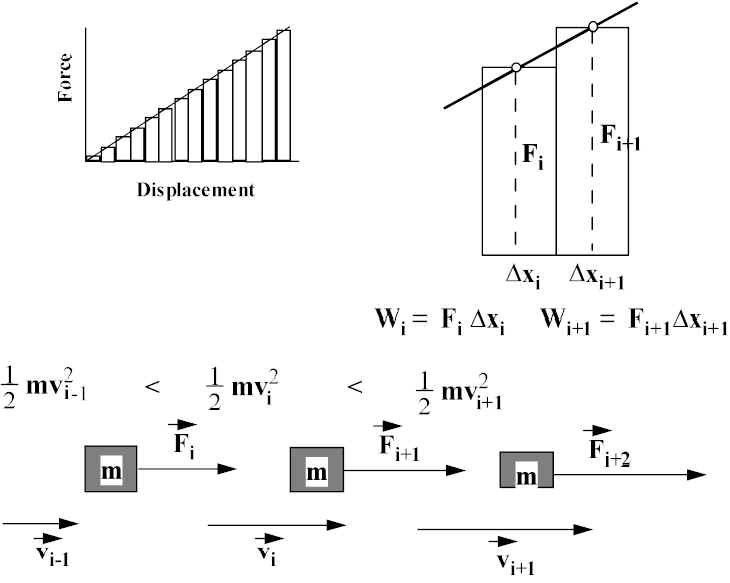
Total work going from x1 to x2 = Wtotal = S FiDxi = area under curve!! (C word = integral of F from x1 to x2) and DKE = Wtotal.

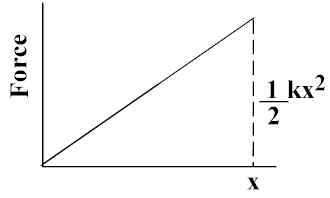
For linear force, F= kx, Area under curve from 0 to xf = .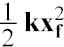

                       

A mass m is moving in a straight line at velocity vo. It comes into contact with a spring with force constant k. How far will the spring compress in bringing the mass to rest?

A spring exerts F proportional to x in both compression and extension (for reasonable x).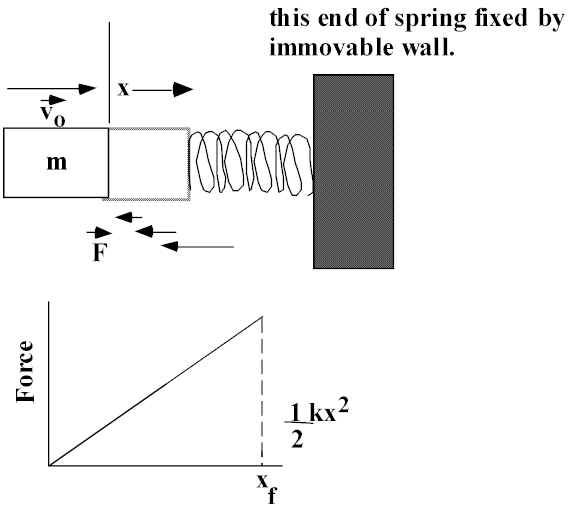

Change in KE = KEf - KEi = 0 - mvo^2. Work done by F on mass, W = - kxf^2. Therefore, kxf^2 = mvo^2 or .
IF we use object and compress spring this same distance (xf = xo) and let go, what is final KE and v? Work done by F on mass, W = +kxo^2.
Change in KE = KEf - KEi = mvf^2 + 0. Therefore, mvf^2 = kxo^2. Since xf = xo, we see that: || = ||. Since we take a , ± does not give direction. Have to go to PICTURE; conclude that . 

Running the Stairs to the Stars (Part rangers Bldg -- Basement to 14th floor); Consider POWER.
1. Who could generate the highest instantaneous power?
2. Who could generate the highest average power?
What are "significant" output levels?
Person in good physical shape -- 1/10 hp (75 W) at steady pace. O2 consumption -- 1 liter (1000 cm3)/minute.
Top athlete -- (long distance sports-runners, skiers, bikers) 0.6 hp (~400 W); O2 consumption -- 5.5 liter/minute. Gossamer: (1979) human powered airplane, piloted by world class biker, crossed English Channel -- averaged 190 W (0.3 hp).
FOR approx. 1 minute spurts - 450 - 500 watts.
For fraction of a second -- several kW.
A 70 kg student runs up 2 flights of stairs (Dh = 7.0 m) in 10 s. Compute the student’s output in doing work against gravity in
(a) watts, (b) hp.
(a) W = FDh/t = mgDh/t = (70 kg) (9.81 m/s2) (7 m)/10s = 480 W
(b) W (in hp) = W (in W)/746 = 480/746 hp = 0.64 hp

The express elevator in M Tower A (MISSI) averages a speed of 550 m/minute in its climb to the 103rd floor ( 408.4 m) above ground. Assume a total load of 1.0 x 103 kg, what is the average power that the lifting motor must provide?
vavg = 550 m/minute x 1 min./60 s = 9.144 m/s.
At constant v, Force to lift = F = mg;
Pavg = Fvavg = (1.0 x 103 kg)(9.144 m/s) = 89.57 kW = 90 kW.
(takes ~44 s to make trip).

You want to loose weight; You therefore want to:
a)Run the stairs once/day as hard as you can, then hit the chips!, or
b) Sustain an activity that burns ~ 1CALORIE/Minute almost every day for 30-60 minutes and don’t hit the chips!
1 CALORIE = 1 Kilocalorie (4.186 kJ). 1 Kcal/minute = 70 Watts (substantial effort). To loose weight have to exercise and diet!!!