What are the real world applications of Laplace transform, especially in computer science?
In Electronic computer science it is hardly used, except maybe in data mining / machine learning.Laplace Transform is heavily used in signal processing. Using Laplace or Fourier transform, you can study a signal in the frequency domain. This can be a powerful tool.For instance, if your signal is smooth over time, it means that, in the frequency domain, you're very likely to find only small frequencies. Similarly, the concept of filtering signal/data is based on a frequency domain interpretation.
The only difference between a Laplace transform and a Fourier transform lies on the domain. A Laplace transform can be seen as a generalization of a Fourier transform. From a system point of view, a Fourier transform gives information on the steady state, while the Laplace gives information on the steady state as well as the transient state.
Laplace transform will convert a function in some domain into a function in another domain, without changing the value of the function.
We use Laplace transform to convert equations having complex differential equations to relatively simple equations having polynomials.
Since equations having polynomials are easier to solve, we employ Laplace transform to make calculations easier.
We use Laplace transform on a derivative to convert it into a multiple of the domain variable. Thus with Laplace transform nth degree differential equation can be transformed into an nth degree polynomial.
One can easily solve the polynomial to get the result and then change it into a differential equation using inverse Laplace transform.
A simple Laplace Transform is conducted while sending signals over any two-way communication medium (FM/AM stereo, 2-way radio sets, cellular phones).
When information is sent over medium such as cellular phones, they are first converted into time-varying wave, and then it is super-imposed on the medium.
In this way, the information propagates. Now, at the receiving end, to decipher the information being sent, medium wave’s time functions are converted to frequency functions.
This is a simple real life application of Laplace Transform.
Engineering Applications of Laplace Transform
Laplace transform has several applications in almost all Engineering disciplines.
1) System Modelling
Laplace transform is used to simplify calculations in system modelling, where large differential equations are used.
2) Analysis of Electrical Circuits
In electrical circuits, a Laplace transform is used for the analysis of linear time-invariant systems.
3) Analysis of Electronic Circuits
Laplace transform is widely used by Electronics engineers to quickly solve differential equations occurring in the analysis of electronic circuits.
4) Digital Signal Processing
One cannot imagine solving DSP (Digital Signal processing) problems without employing Laplace transform.
5) Nuclear Physics
In order to get the true form of radioactive decay, a Laplace transform is used. It makes studying analytic part of Nuclear Physics possible.
6) Process Controls
Laplace transforms are critical for process controls. It helps analyze the variables, which when altered, produces desired manipulations in the result. For example, while study heat experiments, Laplace transform is used to find out to what extent the given input can be altered by changing temperature, hence one can alter temperature to get desired output for a while. This is an efficient and easier way to control processes that are guided by differential equations.
Laplace transform converts complex ordinary differential equations (ODEs) into differential equations that have polynomials in it.
Solving a equation with polynomials in it is easier, this is why we use it. It reduces the complexity of the problem and time taken to solve it.
Once we have the solution, we can use Inv Laplace transform and get the result in the complex form.
Practical uses:-
- sending signals over any two-way communication medium
- study of control systems
- analysis of HVAC (Heating, Ventilation and Air Conditioning)
- simplify calculations in system modelling
- analysis of linear time-invariant systems
- quickly solve differential equations occurring in the analysis of electronic circuits
The original main use for Laplace transforms was (and is) to solve initial value problems for linear ordinary and partial differential equations. They can reduce ordinary differential equations to algebraic equations, and partial differential equations to odes. The transformed equations are easier to solve, and then the solution in the Laplace domain is transformed back to the time domain, usually by consulting a table of inverse Laplace transforms; if necessary by evaluating the Bromwich contour integral in the complex plane.
Laplace transformation techniques made rigorous earlier ad hoc operator methods, in which the differential with respect to time is replaced by an operator D, with 1/D being integration. The operator D is then treated as if it is an algebraic quantity.
The operator technique was fully developed by the physicist Oliver Heaviside in 1893, in connection with his work in telegraphy. Guided greatly by intuition and his wealth of knowledge on the physics behind his circuit studies, Heaviside developed the operational calculus now ascribed to his name.
A rigorous mathematical justification of Heaviside's operational methods came only after the work of Bromwich that related operational calculus with Laplace transformation methods.
Laplace transforms are similar to Fourier in that they transform differential relations to algebraic ones, but differ in that it is often (much) easier to do a LT than its inverse.
This makes them a useful tool when proving stability of linear evolution differential equations and their numerical solutions. The general goal is to show that some norm (typically energy) of the error stays bound over time, and using a LT, this translates to bounding a linear operator *. The point is that one does not need to reconstruct the solution, only bound it, hence the inverse transform is not needed.
Applications of Laplace Equation
Laplace transform: The Laplace transform is an integral transform, second only to the Fourier transform in its utility in solving physical problems. The Laplace transform is particularly useful in solving linear ordinary differential equations such as those arising in the analysis of electronic circuits, control system etc
Data mining/machine learning: Machine learning focuses on prediction, based on known properties learned from the training data. Data mining (which is the analysis step of Knowledge Discovery in Databases) focuses on the discovery of (previously) unknown properties on the data. Where Laplace equation is used to determine the prediction and to analyses the step of knowledge in databases.
Signal processing: Laplace Transform is heavily used in signal processing. Using Laplace or Fourier transform, we can study a signal in the frequency domain. Laplace transform is a subset of the Fourier transform which is used in the processing of data signals during their transmission. For instance, if the signal is smooth over time, it means that, in the frequency domain, we are very likely to find only small frequencies. Similarly, the concept of filtering signal/data is based on a frequency domain interpretation. That is catching and cleaning of errors generated during transmission of computer data.
Instrumentation and Control systems: A control system manages commands, directs or regulates the behavior of other devices or systems. It can range from a home heating controller using a thermostat controlling a domestic boiler to large Industrial control systems which are used for controlling processes or machines. The Laplace transform converts the governing differential equations of a system or its components into simple algebraic form allowing the controls engineer to describe the system, in particular a closed loop system, as a chain of connected functional blocks also called a block diagram.
Integrated circuit: Laplace Transformations helps to find out the current and some criteria for the analyzing the circuits. It is used to build required ICs and chips for systems. So it plays a vital role in field of Electronics computer science.
The primary application is that it lets you solve several differential equations by transforming them to simpler differential equations. Since all sorts of problems in science and engineering can be reduced to differential equations, this makes it an extremely applicable technique.
Signal Processing is one area where you need a very good knowledge of computer science as well as math. Since almost all of signal theory is based on Laplace , Fourier and the Z-transforms, it is a key component in helping you understand what actually is happening behind the scenes. If you have taken/will take/ are doing a course in signal theory, you will realize the importance.
XXX . XXX Linear circuit
A linear circuit is an electronic circuit in which, for a sinusoidal input voltage of frequency f, any steady-state output of the circuit (the current through any component, or the voltage between any two points) is also sinusoidal with frequency f. Note that the output need not be in phase with the input.
An equivalent definition of a linear circuit is that it obeys the superposition principle. This means that the output of the circuit F(x) when a linear combination of signals ax1(t) + bx2(t) is applied to it is equal to the linear combination of the outputs due to the signals x1(t) and x2(t) applied separately:
Linear and nonlinear components
A linear circuit is one that has no nonlinear electronic components in it. Examples of linear circuits are amplifiers, differentiators, and integrators, linear electronic filters, or any circuit composed exclusively of ideal resistors, capacitors, inductors, op-amps (in the "non-saturated" region), and other "linear" circuit elements.Some examples of nonlinear electronic components are: diodes, transistors, and iron core inductors and transformers when the core is saturated. Some examples of circuits that operate in a nonlinear way are mixers, modulators, rectifiers, radio receiver detectors and digital logic circuits.
Significance
Linear circuits are important because they can process analog signals without introducing intermodulation distortion. This means that separate frequencies in the signal stay separate and do not mix, creating new frequencies (heterodynes).They are also easier to understand. Because they obey the superposition principle, linear circuits can be analyzed with powerful mathematical frequency domain techniques, including Fourier analysis and the Laplace transform. These also give an intuitive understanding of the qualitative behavior of the circuit, characterizing it using terms such as gain, phase shift, resonant frequency, bandwidth, Q factor, poles, and zeros. The analysis of a linear circuit can often be done by hand using a scientific calculator.
In contrast, nonlinear circuits usually do not have closed form solutions. They must be analyzed using approximate numerical methods by electronic circuit simulation computer programs such as SPICE, if accurate results are desired. The behavior of such linear circuit elements as resistors, capacitors, and inductors can be specified by a single number (resistance, capacitance, inductance, respectively). In contrast, a nonlinear element's behavior is specified by its detailed transfer function, which may be given as a graph. So specifying the characteristics of a nonlinear circuit requires more information than is needed for a linear circuit.
"Linear" circuits and systems form a separate category within electronic manufacturing. Manufacturers of transistors and integrated circuits often divide their product lines into 'linear' and 'digital' lines. "Linear" here means "analog"; the linear line includes integrated circuits designed to process signals linearly, such as op-amps, audio amplifiers, and active filters, as well as a variety of signal processing circuits that implement nonlinear analog functions such as logarithmic amplifiers, analog multipliers, and peak detectors.
Small signal approximation
Nonlinear elements such as transistors tend to behave linearly when small AC signals are applied to them. So in analyzing many circuits where the signal levels are small, for example those in TV and radio receivers, nonlinear elements can be replaced with a linear small - signal model , allowing linear analysis techniques to be used.Conversely, all circuit elements, even "linear" elements, show nonlinearity as the signal level is increased. If nothing else, the power supply voltage to the circuit usually puts a limit on the magnitude of voltage output from a circuit. Above that limit, the output ceases to scale in magnitude with the input, failing the definition of linearity.
Laplace transform is a more general form of fourier transform. Laplace transform can be applied to all signals, and all systems. Fourier transform of a system exists only if a system is stable, i.e, only if the region of convergence in the pole - zero plot of the laplace transform includes the jw- axis. If it includes, then it means the fourier transform exists.
If the transform is 1/(1-s), there exists a pole in the right half of the s-plane at s=1. This system has a time domain representation of exp(t)*u(t) or exp(-t)*u(-t). If you notice, these signals are not absolutely
integrable in their respective intervals. So, it doesn't satisfy dirichlet's condition. Hence, the fourier transform doesn't exist.
the system exists, but it can't be analysed in the fourier domain. By implementation, if you mean implementation using circuits, you can just use a diode, resistance, opamp circuit to implement it.
If at all, it exists, yeah both will have the same magnitude. The phase of the 1/(1+jw) system will be -tan inverse( w) and the phase of 1/(1-jw) will be -tan inverse(-w).
use a diode, resistance, op amp circuit to implement it can be analyzed in the fourier domain . the system exists, but it can't be analyzed in the fourier domain. By implementation, if you mean implementation using circuits, you can just use a diode, resistance, op amp circuit to implement it.
If at all, it exists, yeah both will have the same magnitude. The phase of the 1/(1+jw) system will be -tan inverse( w) and the phase of 1/(1-jw) will be -tan inverse(-w).
the circuit diagram :
As i mentioned earlier, the system is not stable. Hence, according to the definition of fourier transform, it can't be analyzed in that domain.
the circuit diagram :
As i mentioned earlier, the system is not stable. Hence, according to the definition of fourier transform, it can't be analyzed in that domain.
the circuit diagram :
As i mentioned earlier, the system is not stable. Hence, according to the definition of fourier transform, it can't be analyzed in that domain.
the object analyzed :
(1) In studying stability of system, an important factor which we have to focus on is "Characteristics Polynomial" not "Input to Output Transfer Function"
(2) Fourier Transformation and Laplace Transformation are mathematically same.
Consider "Analytic Continuation" in complex function theory.
Especially they are completely same for causal function.
(3) Even if you characterize circuit by H(jw) instead of H(s), "eigen mode" is same.
So there is no difference between H(jw) and H(s) regarding "eigen mode".
(4) Even if gain is lesser than 0dB, circuit could be unstable.
Here you have to understand "eigen mode".
(5) In small signal AC analysis, "eigen mode" is never generated.
Consider time domain equation in stead of AC analysis.
(6) Consider simple RC-low pass filter.
H(jw)=1/(1+j*w/wc), where wc=R*C.
If R is negative, wc is negative.
Consider time domain phenomena,.
If "eigen mode", exp (-t*wc) excited by some noise will grow infinitely since wc<0. This is due to negative resistance.
The world we live in is getting more and digital with electronic embedded systems surrounding us and communicating with the cloud. However, the physical world is analog in essence. The digital embedded systems thus need analog functions to interact with the physical world, its users, the cloud, the energy sources, as well as between themselves. This is done through sensors, actuators, user interfaces, power management units, wire line and wireless communications. Digital systems also rely on key analog functions performed internally for efficient operation: memories, clocking and voltage regulation. In this course, we study the architecture of the key analog electronic systems performing these functions.
continuous-time signal representation both in time and frequency domains, mathematical system representations (transfer function, impulse response, stability, filtering), principles and properties of Fourier and Laplace transforms, analysis of electrical circuits based on passive components (R, L, C), in DC, transient and AC regimes, understanding of general behavior of operational amplifiers, diodes and transistors with the associated basic electronic circuits, as they are covered with Laplace and
Fourier transform Analyzed .
XXX . XXX 4%zero null 0 Digital signal processing
Digital signal processing (DSP) is the use of digital processing, such as by computers or more specialized digital signal processors, to perform a wide variety of signal processing operations. The signals processed in this manner are a sequence of numbers that represent samples of a continuous variable in a domain such as time, space, or frequency.
Digital signal processing and analog signal processing are subfields of signal processing. DSP applications include audio and speech processing, sonar, radar and other sensor array processing, spectral density estimation, statistical signal processing, digital image processing, signal processing for telecommunications, control systems, biomedical engineering, seismology, among others.
DSP can involve linear or nonlinear operations. Nonlinear signal processing is closely related to nonlinear system identification[1] and can be implemented in the time, frequency, and spatio-temporal domains.
The application of digital computation to signal processing allows for many advantages over analog processing in many applications, such as error detection and correction in transmission as well as data compression. DSP is applicable to both streaming data and static (stored) data.
Signal sampling
To digitally analyze and manipulate an analog signal, it must be digitized with an analog-to-digital converter (ADC). Sampling is usually carried out in two stages, discretization and quantization. Discretization means that the signal is divided into equal intervals of time, and each interval is represented by a single measurement of amplitude. Quantization means each amplitude measurement is approximated by a value from a finite set. Rounding real numbers to integers is an example.The Nyquist–Shannon sampling theorem states that a signal can be exactly reconstructed from its samples if the sampling frequency is greater than twice the highest frequency component in the signal. In practice, the sampling frequency is often significantly higher than twice the Nyquist frequency.
Theoretical DSP analyses and derivations are typically performed on discrete-time signal models with no amplitude inaccuracies (quantization error), "created" by the abstract process of sampling. Numerical methods require a quantized signal, such as those produced by an ADC. The processed result might be a frequency spectrum or a set of statistics. But often it is another quantized signal that is converted back to analog form by a digital-to-analog converter (DAC).
Domains
In DSP, engineers usually study digital signals in one of the following domains: time domain (one-dimensional signals), spatial domain (multidimensional signals), frequency domain, and wavelet domains. They choose the domain in which to process a signal by making an informed assumption (or by trying different possibilities) as to which domain best represents the essential characteristics of the signal and the processing to be appied to it. A sequence of samples from a measuring device produces a temporal or spatial domain representation, whereas a discrete Fourier transform produces the frequency domain representation.Time and space domains
The most common processing approach in the time or space domain is enhancement of the input signal through a method called filtering. Digital filtering generally consists of some linear transformation of a number of surrounding samples around the current sample of the input or output signal. There are various ways to characterize filters; for example:- A linear filter is a linear transformation of input samples; other filters are nonlinear. Linear filters satisfy the superposition principle, i.e. if an input is a weighted linear combination of different signals, the output is a similarly weighted linear combination of the corresponding output signals.
- A causal filter uses only previous samples of the input or output signals; while a non-causal filter uses future input samples. A non-causal filter can usually be changed into a causal filter by adding a delay to it.
- A time-invariant filter has constant properties over time; other filters such as adaptive filters change in time.
- A stable filter produces an output that converges to a constant value with time, or remains bounded within a finite interval. An unstable filter can produce an output that grows without bounds, with bounded or even zero input.
- A finite impulse response (FIR) filter uses only the input signals, while an infinite impulse response (IIR) filter uses both the input signal and previous samples of the output signal. FIR filters are always stable, while IIR filters may be unstable.
The output of a linear digital filter to any given input may be calculated by convolving the input signal with the impulse response.
Frequency domain
Signals are converted from time or space domain to the frequency domain usually through the Fourier transform. The Fourier transform converts the signal information to a magnitude and phase component of each frequency. Often the Fourier transform is converted to the power spectrum, which is the magnitude of each frequency component squared.The most common purpose for analysis of signals in the frequency domain is analysis of signal properties. The engineer can study the spectrum to determine which frequencies are present in the input signal and which are missing.
In addition to frequency information, phase information is often needed. This can be obtained from the Fourier transform. With some applications, how the phase varies with frequency can be a significant consideration.
Filtering, particularly in non-realtime work can also be achieved by converting to the frequency domain, applying the filter and then converting back to the time domain. This is a fast, O(n log n) operation, and can give essentially any filter shape including excellent approximations to brickwall filters.
There are some commonly used frequency domain transformations. For example, the cepstrum converts a signal to the frequency domain through Fourier transform, takes the logarithm, then applies another Fourier transform. This emphasizes the harmonic structure of the original spectrum.
Frequency domain analysis is also called spectrum- or spectral analysis.
Z-plane analysis
Digital filters come in both IIR and FIR types. FIR filters have many advantages, but are computationally more demanding. Whereas FIR filters are always stable, IIR filters have feedback loops that may resonate when stimulated with certain input signals. The Z-transform provides a tool for analyzing potential stability issues of digital IIR filters. It is analogous to the Laplace transform, which is used to design analog IIR filters.Wavelet

An example of the 2D discrete wavelet transform that is used in JPEG2000. The original image is high-pass filtered, yielding the three large images, each describing local changes in brightness (details) in the original image. It is then low-pass filtered and downscaled, yielding an approximation image; this image is high-pass filtered to produce the three smaller detail images, and low-pass filtered to produce the final approximation image in the upper-left.
Applications
The main applications of DSP are audio signal processing, audio compression, digital image processing, video compression, speech processing, speech recognition, digital communications, digital synthesizers, radar, sonar, financial signal processing, seismology and biomedicine. Specific examples are speech compression and transmission in digital mobile phones, room correction of sound in hi-fi and sound reinforcement applications, weather forecasting, economic forecasting, seismic data processing, analysis and control of industrial processes, medical imaging such as CAT scans and MRI, MP3 compression, computer graphics, image manipulation, hi-fi loudspeaker crossovers and equalization, and audio effects for use with electric guitar amplifiers.Implementation
DSP algorithms have long been run on general-purpose computers and digital signal processors. DSP algorithms are also implemented on purpose-built hardware such as application-specific integrated circuit (ASICs). Additional technologies for digital signal processing include more powerful general purpose microprocessors, field-programmable gate arrays (FPGAs), digital signal controllers (mostly for industrial applications such as motor control), and stream processors.[3]Depending on the requirements of the application, digital signal processing tasks can be implemented on general purpose computers.
Often when the processing requirement is not real-time, processing is economically done with an existing general-purpose computer and the signal data (either input or output) exists in data files. This is essentially no different from any other data processing, except DSP mathematical techniques (such as the FFT) are used, and the sampled data is usually assumed to be uniformly sampled in time or space. For example: processing digital photographs with software such as Photoshop.
However, when the application requirement is real-time, DSP is often implemented using specialized microprocessors such as the DSP56000, the TMS320, or the SHARC. These often process data using fixed-point arithmetic, though some more powerful versions use floating point. For faster applications FPGAs[4] might be used. Beginning in 2007, multicore implementations of DSPs have started to emerge from companies including Frees cale and Stream Processors, Inc. For faster applications with vast usage, ASICs might be designed specifically. For slow applications, a traditional slower processor such as a microcontroller may be adequate. Also a growing number of DSP applications are now being implemented on embedded systems using powerful PCs with multi-core processors.
XXX . XXX 4%zero null 0 1 Discrete-time Fourier transform
In mathematics, the discrete-time Fourier transform (DTFT) is a form of Fourier analysis that is applicable to the uniformly-spaced samples of a continuous function. The term discrete-time refers to the fact that the transform operates on discrete data (samples) whose interval often has units of time. From only the samples, it produces a function of frequency that is a periodic summation of the continuous Fourier transform of the original continuous function. Under certain theoretical conditions, described by the sampling theorem, the original continuous function can be recovered perfectly from the DTFT and thus from the original discrete samples. The DTFT itself is a continuous function of frequency, but discrete samples of it can be readily calculated via the discrete Fourier transform (DFT) (see Sampling the DTFT), which is by far the most common method of modern Fourier analysis.
Both transforms are invertible. The inverse DTFT is the original sampled data sequence. The inverse DFT is a periodic summation of the original sequence. The fast Fourier transform (FFT) is an algorithm for computing one cycle of the DFT, and its inverse produces one cycle of the inverse DFT.
Definition
The discrete-time Fourier transform of a discrete set of real or complex numbers x[n], for all integers n, is a Fourier series, which produces a periodic function of a frequency variable. When the frequency variable, ω, has normalized units of radians/sample, the periodicity is 2π, and the Fourier series is:- (Eq.1)
- (Eq.2)
We also note that is the Fourier transform of Therefore, an alternative definition of DTFT is:[note 1]
- (Eq.3)
Inverse transform
An operation that recovers the discrete data sequence from the DTFT function is called an inverse DTFT. For instance, the inverse continuous Fourier transform of both sides of Eq.3 produces the sequence in the form of a modulated Dirac comb function:Periodic data
When the input data sequence x[n] is N-periodic, Eq.2 can be computationally reduced to a discrete Fourier transform (DFT), because:- All the available information is contained within N samples.
- converges to zero everywhere except integer multiples of known as harmonic frequencies.
- The DTFT is periodic, so the maximum number of unique harmonic amplitudes is
Sampling the DTFT
When the DTFT is continuous, a common practice is to compute an arbitrary number of samples (N) of one cycle of the periodic function X1/T:In order to evaluate one cycle of xN numerically, we require a finite-length x[n] sequence. For instance, a long sequence might be truncated by a window function of length L resulting in two cases worthy of special mention: L ≤ N and L = I•N, for some integer I (typically 6 or 8). For notational simplicity, consider the x[n] values below to represent the modified values.
When L = I•N a cycle of xN reduces to a summation of I blocks of length N. This goes by various names, such as:
- window-presum FFT
- Weight, OverLap, Add (WOLA)[note 4]
- polyphase FFT
- multiple block windowing
- time-aliasing.
When L ≤ N the DFT is usually written in this more familiar form:
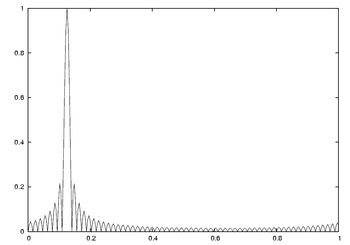
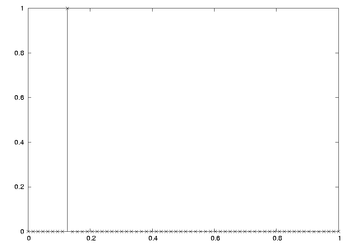
Spectral leakage, which increases as L decreases, is detrimental to certain important performance metrics, such as resolution of multiple frequency components and the amount of noise measured by each DTFT sample. But those things don't always matter, for instance when the x[n] sequence is a noiseless sinusoid (or a constant), shaped by a window function. Then it is a common practice to use zero-padding to graphically display and compare the detailed leakage patterns of window functions. To illustrate that for a rectangular window, consider the sequence:
- and
Convolution
The convolution theorem for sequences is:DTFT of real signals
A complex discrete-time signal is a real signal (i.e if ) if and only if its DTFT is conjugate symmetric.Spectrum of symmetric signals
If is an even symmetric signal (i.e. if ), then the DTFT is real for all .If is an odd symmetric signal (i.e. if ), then the DTFT is purely imaginary for all .
Relationship to the Z-transform
The bilateral Z-transform is defined by:- where z is a complex variable.
Table of discrete-time Fourier transforms
Some common transform pairs are shown in the table below. The following notation applies:- ω = 2πfT is a real number representing continuous angular frequency (in radians per sample). (f is in cycles/sec, and T is in sec/sample.) In all cases in the table, the DTFT is 2π-periodic (in ω).
- X2π(ω) designates a function defined on −∞ < ω < ∞.
- Xo(ω) designates a function defined on −π < ω ≤ π, and zero elsewhere. Then:
- δ(ω) is the Dirac delta function
- sinc(t) is the normalized sinc function
- rect(t) is the rectangle function
- tri(t) is the triangle function
- n is an integer representing the discrete-time domain (in samples)
- u[n] is the discrete-time unit step function
- δ[n] is the Kronecker delta δn, 0
| Time domain x[n] | Frequency domain X2π(ω) | Remarks |
|---|---|---|
| integer M | ||
| odd M even M | integer M > 0 | |
| The term must be interpreted as a distribution in the sense of a Cauchy principal value around its poles at ω = 2πk. | ||
| -π < a < π | real number a | |
| real number a; –π < a < π | ||
| real number a; –π < a < π | ||
| integer M | ||
| real number a | ||
| real number W 0 < W < 1 | ||
| real number W 0 < W < 0.5 | ||
| it works as a differentiator filter | ||
| real numbers W, a 0 < W = 1 | ||
| Hilbert transform | ||
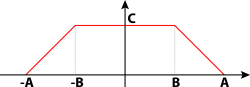 | real numbers A, B complex C |
Properties
This table shows some mathematical operations in the time domain and the corresponding effects in the frequency domain.- is the discrete convolution of two sequences
- x[n]* is the complex conjugate of x[n]
| Property | Time domain | Frequency domain | Remarks |
|---|---|---|---|
| Linearity | |||
| Shift in time / Modulation in frequency | integer k | ||
| Shift in frequency / Modulation in time | real number a | ||
| Down-sampling | [note 5] | integer M | |
| Expansion | integer M | ||
| Time reversal / Frequency reversal | |||
| Time conjugation | |||
| Time reversal & conjugation | |||
| Derivative in frequency | |||
| Integration in frequency | |||
| Differencing in time | |||
| Convolution in time / Multiplication in frequency | |||
| Multiplication in time / Convolution in frequency | Periodic convolution | ||
| Cross correlation | |||
| Parseval's theorem |
XXX . XXX 4%zero null 0 1 2 Multidimensional transform
In mathematical analysis and applications, multidimensional transforms are used to analyze the frequency content of signals in a domain of two or more dimensions.
Multidimensional Fourier transform
One of the more popular multidimensional transforms is the Fourier transform, which converts a signal from a time/space domain representation to a frequency domain representation. The discrete-domain multidimensional Fourier transform (FT) can be computed as follows:Properties of Fourier transform
Similar properties of the 1-D FT transform apply, but instead of the input parameter being just a single entry, it's a Multi-dimensional (MD) array or vector. Hence, it's x(n1,…,nM) instead of x(n).Linearity
if , and then,Shift
if , thenModulation
if , thenMultiplication
if , andthen,
- (MD Convolution in Frequency Domain)
- (MD Convolution in Frequency Domain)
Differentiation
If , thenTransposition
If , thenReflection
If , thenComplex conjugation
If , thenParseval's theorem (MD)
if , and then,if , then
A special case of the Parseval's theorem is when the two multi-dimensional signals are the same. In this case, the theorem portrays the energy conservation of the signal and the term in the summation or integral is the energy-density of the signal.
Separability
One property is the separability property. A signal or system is said to be separable if it can be expressed as a product of 1-D functions with different independent variables. This phenomenon allows computing the FT transform as a product of 1-D FTs instead of multi-dimensional FT.if , , ... , and if , then
, so
MD FFT
A fast Fourier transform (FFT) is an algorithm to compute the discrete Fourier transform (DFT) and its inverse. An FFT computes the DFT and produces exactly the same result as evaluating the DFT definition directly; the only difference is that an FFT is much faster. (In the presence of round-off error, many FFT algorithms are also much more accurate than evaluating the DFT definition directly).There are many different FFT algorithms involving a wide range of mathematics, from simple complex-number arithmetic to group theory and number theory. See more in FFT.MD DFT
The multidimensional discrete Fourier transform (DFT) is a sampled version of the discrete-domain FT by evaluating it at sample frequencies that are uniformly spaced.[2] The N1 × N2 × ... Nm DFT is given by:The inverse multidimensional DFT equation is
Multidimensional discrete cosine transform
The discrete cosine transform (DCT) is used in a wide range of applications such as data compression, feature extraction, Image reconstruction, multi-frame detection and so on. The multidimensional DCT is given by:Multidimensional Laplace transform
The multidimensional Laplace transform is useful for the solution of boundary value problems. Boundary value problems in two or more variables characterized by partial differential equations can be solved by a direct use of the Laplace transform. The Laplace transform for an M-dimensional case is defined aswhere F stands for the s-domain representation of the signal f(t).
A special case (along 2 dimensions) of the multi-dimensional Laplace transform of function f(x,y) is defined[4] as
is called the image of and is known as the original of . This special case can be used to solve the Telegrapher's equations.
Multidimensional Z transform
The multidimensional Z transform is used to map the discrete time domain multidimensional signal to the Z domain. This can be used to check the stability of filters. The equation of the multidimensional Z transform is given bywhere F stands for the z-domain representation of the signal f(n).
A special case of the multidimensional Z transform is the 2D Z transform which is given as
The Fourier transform is a special case of the Z transform evaluated along the unit circle (in 1D) and unit bi-circle (in 2D). i.e. at
where z and w are vectors.
Region of convergence
Points (z1,z2) for which are located in the ROC.An example:
If a sequence has a support as shown in Figure 1.1a, then its ROC is shown in Figure 1.1b. This follows that |F(z1,z2)| < ∞ .
lies in the ROC, then all pointsthat satisfy |z1|≥|z01| and |z2|≥|z02 lie in the ROC.
Therefore, for figure 1.1a and 1.1b, the ROC would be
The 2D Z-transform, similar to the Z-transform, is used in multidimensional signal processing to relate a two-dimensional discrete-time signal to the complex frequency domain in which the 2D surface in 4D space that the Fourier transform lies on is known as the unit surface or unit bicircle.
Applications
The DCT and DFT are often used in signal processing and image processing, and they are also used to efficiently solve partial differential equations by spectral methods. The DFT can also be used to perform other operations such as convolutions or multiplying large integers. The DFT and DCT have seen wide usage across a large number of fields, we only sketch a few examples below.Image processing
In image processing, one can also analyze and describe unconventional cryptographic methods based on 2D DCTs, for inserting non-visible binary watermarks into the 2D image plane,[8] and According to different orientations, the 2-D directional DCT-DWT hybrid transform can be applied in denoising ultrasound images.[9] 3-D DCT can also be used to transform video data or 3-D image data in watermark embedding schemes in transform domain.[10][11]
Spectral analysis
When the DFT is used for spectral analysis, the {xn} sequence usually represents a finite set of uniformly spaced time-samples of some signal x(t) where t represents time. The conversion from continuous time to samples (discrete-time) changes the underlying Fourier transform of x(t) into a discrete-time Fourier transform (DTFT), which generally entails a type of distortion called aliasing. Choice of an appropriate sample-rate (see Nyquist rate) is the key to minimizing that distortion. Similarly, the conversion from a very long (or infinite) sequence to a manageable size entails a type of distortion called leakage, which is manifested as a loss of detail (aka resolution) in the DTFT. Choice of an appropriate sub-sequence length is the primary key to minimizing that effect. When the available data (and time to process it) is more than the amount needed to attain the desired frequency resolution, a standard technique is to perform multiple DFTs, for example to create a spectrogram. If the desired result is a power spectrum and noise or randomness is present in the data, averaging the magnitude components of the multiple DFTs is a useful procedure to reduce the variance of the spectrum (also called a periodogram in this context); two examples of such techniques are the Welch method and the Bartlett method; the general subject of estimating the power spectrum of a noisy signal is called spectral estimation.A final source of distortion (or perhaps illusion) is the DFT itself, because it is just a discrete sampling of the DTFT, which is a function of a continuous frequency domain. That can be mitigated by increasing the resolution of the DFT. That procedure is illustrated at Sampling the DTFT.
- The procedure is sometimes referred to as zero-padding, which is a particular implementation used in conjunction with the fast Fourier transform (FFT) algorithm. The inefficiency of performing multiplications and additions with zero-valued "samples" is more than offset by the inherent efficiency of the FFT.
- As already noted, leakage imposes a limit on the inherent resolution of the DTFT. So there is a practical limit to the benefit that can be obtained from a fine-grained DFT.
Partial differential equations
Discrete Fourier transforms are often used to solve partial differential equations, where again the DFT is used as an approximation for the Fourier series (which is recovered in the limit of infinite N). The advantage of this approach is that it expands the signal in complex exponentials einx, which are eigenfunctions of differentiation: d/dx einx = in einx. Thus, in the Fourier representation, differentiation is simple—we just multiply by i n. (Note, however, that the choice of n is not unique due to aliasing; for the method to be convergent, a choice similar to that in the trigonometric interpolation section above should be used.) A linear differential equation with constant coefficients is transformed into an easily solvable algebraic equation. One then uses the inverse DFT to transform the result back into the ordinary spatial representation. Such an approach is called a spectral method.DCTs are also widely employed in solving partial differential equations by spectral methods, where the different variants of the DCT correspond to slightly different even/odd boundary conditions at the two ends of the array.
Laplace transforms are used to solve partial differential equations. The general theory for obtaining solutions in this technique is developed by theorems on Laplace transform in n dimensions.
The multidimensional Z transform can also be used to solve partial differential equations.
Image processing for arts surface analysis by FFT
One very important factor is that we must apply a non-destructive method to obtain those rare valuables information (from the HVS viewing point, is focused in whole colorimetric and spatial information) about works of art and zero-damage on them. We can understand the arts by looking at a color change or by measuring the surface uniformity change. Since the whole image will be very huge, so we use a double raised cosine window to truncate the image:Application to weakly nonlinear circuit simulation
The inverse multidimensional Laplace transform can be applied to simulate nonlinear circuits. This is done so by formulating a circuit as a state-space and expanding the Inverse Laplace Transform based on Laguerre function expansion.The Lagurre method can be used to simulate a weakly nonlinear circuit and the Laguerre method can invert a multidimensional Laplace transform efficiently with a high accuracy.
It is observed that a high accuracy and significant speedup can be achieved for simulating large nonlinear circuits using multidimensional Laplace transforms.
multidimensional discrete convolution
In signal processing, multidimensional discrete convolution refers to the mathematical operation between two functions f and g on an n-dimensional lattice that produces a third function, also of n-dimensions. Multidimensional discrete convolution is the discrete analog of the multidimensional convolution of functions on Euclidean space. It is also a special case of convolution on groups when the group is the group of n-tuples of integers.
Definition
Problem Statement & Basics
Similar to the one-dimensional case, an asterisk is used to represent the convolution operation. The number of dimensions in the given operation is reflected in the number of asterisks. For example, an M-dimensional convolution would be written with M asterisks. The following represents a M-dimensional convolution of discrete signals:For discrete-valued signals, this convolution can be directly computed via the following:
The resulting output region of support of a discrete multidimensional convolution will be determined based on the size and regions of support of the two input signals.
Listed are several properties of the two-dimensional convolution operator. Note that these can also be extended for signals of -dimensions.
Commutative Property:
Associate Property:
Distributive Property:
These properties are seen in use in the figure below. Given some input that goes into a filter with impulse response and then another filter with impulse response , the output is given by . Assume that the output of the first filter is given by , this means that:
Further, that intermediate function is then convolved with the impulse response of the second filter, and thus the output can be represented by:
Using the associative property, this can be rewritten as follows:
meaning that the equivalent impulse response for a cascaded system is given by:
In this case, it is clear that:
Using the distributive law, it is demonstrated that:
This means that in the case of a parallel system, the equivalent impulse response is provided by:
The equivalent impulse responses in both cascaded systems and parallel systems can be generalized to systems with -number of filters.[1]
Motivation & Applications
Convolution in one dimension was a powerful discovery that allowed the input and output of a linear shift-invariant (LSI) system (see LTI system theory). to be easily compared so long as the impulse response of the filter system was known. This notion carries over to multidimensional convolution as well, as simply knowing the impulse response of a multidimensional filter too allows for a direct comparison to be made between the input and output of a system. This is profound since several of the signals that are transferred in the digital world today are of multiple dimensions including images and videos. Similar to the one-dimensional convolution, the multidimensional convolution allows the computation of the output of an LSI system for a given input signal.For example, consider an image that is sent over some wireless network subject to electrooptical noise. Possible noise sources include errors in channel transmission, the analog to digital converter, and the image sensor. Usually noise caused by the channel or sensor creates spatially-independent, high-frequency signal components that translates to arbitrary light and dark spots on the actual image. In order to rid the image data of the high-frequency spectral content, it can be multiplied by the frequency response of a low-pass filter, which based on the convolution theorem, is equivalent to convolving the signal in the time/spatial domain by the impulse response of the low-pass filter. Several impulse responses that do so are shown below.[2]
In addition to filtering out spectral content, the multidimensional convolution can implement edge detection and smoothing. This once again is wholly dependent on the values of the impulse response that is used to convolve with the input image. Typical impulse responses for edge detection are illustrated below.
In addition to image processing, multidimensional convolution can be implemented to enable a variety of other applications. Since filters are widespread in digital communication systems, any system that must transmit multidimensional data is assisted by filtering techniques It is used in real-time video processing, neural network analysis, digital geophysical data analysis, and much more.[3]
One typical distortion that occurs during image and video capture or transmission applications is blur that is caused by a low-pass filtering process. The introduced blur can be modeled using Gaussian low-pass filtering.
Row-Column Decomposition with Separable Signals
Separable Signals
A signal is said to be separable if it can be written as the product of multiple one-dimensional signals.[1] Mathematically, this is expressed as the following:Some readily recognizable separable signals include the unit step function, and the delta-dirac impulse function.
(unit step function)
(delta-dirac impulse function)
Convolution is a linear operation. It then follows that the multidimensional convolution of separable signals can be expressed as the product of many one-dimensional convolutions. For example, consider the case where x and h are both separable functions.
By applying the properties of separability, this can then be rewritten as the following:
It is readily seen then that this reduces to the product of one-dimensional convolutions:
This conclusion can then be extended to the convolution of two separable M-dimensional signals as follows:
So, when the two signals are separable, the multidimensional convolution can be computed by computing one-dimensional convolutions.
Row-Column Decomposition
The row-column method can be applied when one of the signals in the convolution is separable. The method exploits the properties of separability in order to achieve a method of calculating the convolution of two multidimensional signals that is more computationally efficient than direct computation of each sample (given that one of the signals are separable).[4] The following shows the mathematical reasoning behind the row-column decomposition approach (typically is the separable signal):Thus, the resulting convolution can be effectively calculated by first performing the convolution operation on all of the rows of , and then on all of its columns. This approach can be further optimized by taking into account how memory is accessed within a computer processor.
A processor will load in the signal data needed for the given operation. For modern processors, data will be loaded from memory into the processors cache, which has faster access times than memory. The cache itself is partitioned into lines. When a cache line is loaded from memory, multiple data operands are loaded at once. Consider the optimized case where a row of signal data can fit entirely within the processor's cache. This particular processor would be able to access the data row-wise efficiently, but not column-wise since different data operands in the same column would lie on different cache lines.[5] In order to take advantage of the way in which memory is accessed, it is more efficient to transpose the data set and then axis it row-wise rather than attempt to access it column-wise. The algorithm then becomes:
- Separate the separable two-dimensional signal into two one-dimensional signals and
- Perform row-wise convolution on the horizontal components of the signal using to obtain
- Transpose the vertical components of the signal resulting from Step 2.
- Perform row-wise convolution on the transposed vertical components of to get the desired output
Computational Speedup from Row-Column Decomposition
Examine the case where an image of size is being passed through a separable filter of size . The image itself is not separable. If the result is calculated using the direct convolution approach without exploiting the separability of the filter, this will require approximately multiplications and additions. If the separability of the filter is taken into account, the filtering can be performed in two steps. The first step will have multiplications and additions and the second step will have , resulting in a total of or multiplications and additions.[6] A comparison of the computational complexity between direct and separable convolution is given in the following image:Circular Convolution of Discrete-Valued Multidimensional Signals
The premise behind the circular convolution approach on multidimensional signals is to develop a relation between the Convolution theorem and the Discrete Fourier transform (DFT) that can be used to calculate the convolution between two finite-extent, discrete-valued signals.Convolution Theorem in Multiple Dimensions
For one-dimensional signals, the Convolution Theorem states that the Fourier transform of the convolution between two signals is equal to the product of the Fourier Transforms of those two signals. Thus, convolution in the time domain is equal to multiplication in the frequency domain. Mathematically, this principle is expressed via the following:When dealing with signals of multiple dimensions:
Circular Convolution Approach
The motivation behind using the circular convolution approach is that it is based on the DFT. The premise behind circular convolution is to take the DFTs of the input signals, multiply them together, and then take the inverse DFT. Care must be taken such that a large enough DFT is used such that aliasing does not occur. The DFT is numerically computable when dealing with signals of finite-extent. One advantage this approach has is that since it requires taking the DFT and inverse DFT, it is possible to utilize efficient algorithms such as the Fast Fourier transform (FFT). Circular convolution can also be computed in the time/spatial domain and not only in the frequency domain.Choosing DFT size to avoid Aliasing
Consider the following case where two finite-extent signals x and h are taken. For both signals, there is a corresponding DFT as follows:and
The region of support of is and and the region of support of is and .
The linear convolution of these two signals would be given as:
for
The result will be that will be a spatially aliased version of the linear convolution result . This can be expressed as the following:
Then, in order to avoid aliasing between the spatially aliased replicas, and must be chosen to satisfy the following conditions:
If these conditions are satisfied, then the results of the circular convolution will equal that of the linear convolution (taking the main period of the circular convolution as the region of support). That is:
for
Summary of Procedure Using DFTs
The Convolution theorem and circular convolution can thus be used in the following manner to achieve a result that is equal to performing the linear convolution:[8]- Choose and to satisfy and
- Zero pad the signals and such that they are both in size
- Compute the DFTs of both and
- Multiple the results of the DFTs to obtain
- The result of the IDFT of will then be equal to the result of performing linear convolution on the two signals
Overlap and Add
Another method to perform multidimensional convolution is the overlap and add approach. This method helps reduce the computational complexity often associated with multidimensional convolutions due to the vast amounts of data inherent in modern-day digital systems.[9] For sake of brevity, the two-dimensional case is used as an example, but the same concepts can be extended to multiple dimensions.Consider a two-dimensional convolution using a direct computation:
Assuming that the output signal has N nonzero coefficients, and the impulse response has M nonzero samples, this direct computation would need MN multiplies and MN - 1 adds in order to compute. Using an FFT instead, the frequency response of the filter and the Fourier transform of the input would have to be stored in memory.] Massive amounts of computations and excessive use of memory storage space pose a problematic issue as more dimensions are added. This is where the overlap and add convolution method comes in.
Decomposition into Smaller Convolution Blocks
Instead of performing convolution on the blocks of information in their entirety, the information can be broken up into smaller blocks of dimensions x resulting in smaller FFTs, less computational complexity, and less storage needed. This can be expressed mathematically as follows:where represents the x input signal, which is a summation of block segments, with and .
To produce the output signal, a two-dimensional convolution is performed:
Substituting in for results in the following:
This convolution adds more complexity than doing a direct convolution; however, since it is integrated with an FFT fast convolution, overlap-add performs faster and is a more memory-efficient method, making it practical for large sets of multidimensional data.
Breakdown of Procedure
Let be of size :- Break input into non-overlapping blocks of dimensions .
- Zero pad such that it has dimensions () ().
- Use DFT to get .
- For each input block:
- Zero pad to be of dimensions () ().
- Take discrete Fourier transform of each block to give .
- Multiply to get .
- Take inverse discrete Fourier transform of to get .
- Find by overlap and adding the last samples of with the first samples of to get the result.
Pictorial Method of Operation
In order to visualize the overlap-add method more clearly, the following illustrations examine the method graphically. Assume that the input has a square region support of length N in both vertical and horizontal directions as shown in the figure below. It is then broken up into four smaller segments in such a way that it is now composed of four smaller squares. Each block of the aggregate signal has dimensions .Then, each component is convolved with the impulse response of the filter. Note that an advantage for an implementation such as this can be visualized here since each of these convolutions can be parallelized on a computer, as long as the computer has sufficient memory and resources to store and compute simultaneously.
In the figure below, the first graph on the left represents the convolution corresponding to the component of the input with the corresponding impulse response . To the right of that, the input is then convolved with the impulse response .
The same process is done for the other two inputs respectively, and they are accumulated together in order to form the convolution. This is depicted to the left.
Assume that the filter impulse response has a region of support of in both dimensions. This entails that each convolution convolves signals with dimensions in both and directions, which leads to overlap (highlighted in blue) since the length of each individual convolution is equivalent to:
=
in both directions. The lighter blue portion correlates to the overlap between two adjacent convolutions, whereas the darker blue portion correlates to overlap between all four convolutions. All of these overlap portions are added together in addition to the convolutions in order to form the combined convolution .
Overlap and Save
The overlap and save method, just like the overlap and add method, is also used to reduce the computational complexity associated with discrete-time convolutions. This method, coupled with the FFT, allows for massive amounts of data to be filtered through a digital system while minimizing the necessary memory space used for computations on massive arrays of data.Comparison to Overlap and Add
The overlap and save method is very similar to the overlap and add methods with a few notable exceptions. The overlap-add method involves a linear convolution of discrete-time signals, whereas the overlap-save method involves the principle of circular convolution. In addition, the overlap and save method only uses a one-time zero padding of the impulse response, while the overlap-add method involves a zero-padding for every convolution on each input component. Instead of using zero padding to prevent time-domain aliasing like its overlap-add counterpart, overlap-save simply discards all points of aliasing, and saves the previous data in one block to be copied into the convolution for the next block.In one dimension, the performance and storage metric differences between the two methods is minimal. However, in the multidimensional convolution case, the overlap-save method is preferred over the overlap-add method in terms of speed and storage abilities.[13] Just as in the overlap and add case, the procedure invokes the two-dimensional case but can easily be extended to all multidimensional procedures.
Breakdown of Procedure
Let be of size :- Insert columns and rows of zeroes at the beginning of the input signal in both dimensions.
- Split the corresponding signal into overlapping segments of dimensions ()() in which each two-dimensional block will overlap by .
- Zero pad such that it has dimensions ()().
- Use DFT to get .
- For each input block:
- Take discrete Fourier transform of each block to give .
- Multiply to get .
- Take inverse discrete Fourier transform of to get .
- Get rid of the first for each output block .
- Find by attaching the last samples for each output block .
The Helix Transform
Similar to row-column decomposition, the helix transform computes the multidimensional convolution by incorporating one-dimensional convolutional properties and operators. Instead of using the separability of signals, however, it maps the Cartesian coordinate space to a helical coordinate space allowing for a mapping from a multidimensional space to a one-dimensional space.Multidimensional Convolution with One-Dimensional Convolution Methods
To understand the helix transform, it is useful to first understand how a multidimensional convolution can be broken down into a one-dimensional convolution. Assume that the two signals to be convolved are and , which results in an output . This is expressed as follows:Next, two matrices are created that zero pad each input in both dimensions such that each input has equivalent dimensions, i.e.
and
where each of the input matrices are now of dimensions . It is then possible to implement column-wise lexicographic ordering in order to convert the modified matrices into vectors, and . In order to minimize the number of unimportant samples in each vector, each vector is truncated after the last sample in the original matrices and respectively. Given this, the length of vector and are given by:
+
+
The length of the convolution of these two vectors, , can be derived and shown to be:
Interestingly, this vector length is equivalent to the dimensions of the original matrix output , making converting back to a matrix a direct transformation. Thus, the vector, , is converted back to matrix form, which produces the output of the two-dimensional discrete convolution.
Filtering on a Helix
When working on a two-dimensional Cartesian mesh, a Fourier transform along either axes will result in the two-dimensional plane becoming a cylinder as the end of each column or row attaches to its respective top forming a cylinder. Filtering on a helix behaves in a similar fashion, except in this case, the bottom of each column attaches to the top of the next column, resulting in a helical mesh. This is illustrated below. The darkened tiles represent the filter coefficients.If this helical structure is then sliced and unwound into a one-dimensional strip, the same filter coefficients on the 2-d Cartesian plane will match up with the same input data, resulting in an equivalent filtering scheme. This ensures that a two-dimensional convolution will be able to be performed by a one-dimensional convolution operator as the 2D filter has been unwound to a 1D filter with gaps of zeroes separating the filter coefficients.
Assuming that some-low pass two-dimensional filter was used, such as:
| 0 | -1 | 0 |
| -1 | 4 | -1 |
| 0 | -1 | 0 |
Notice in the one-dimensional filter that there are no leading zeroes as illustrated in the one-dimensional filtering strip after being unwound. The entire one-dimensional strip could have been convolved with; however, it is less computationally expensive to simply ignore the leading zeroes. In addition, none of these backside zero values will need to be stored in memory, preserving precious memory resources.[15]
Applications
Helix transformations to implement recursive filters via convolution are used in various areas of signal processing. Although frequency domain Fourier analysis is effective when systems are stationary, with constant coefficients and periodically-sampled data, it becomes more difficult in unstable systems. The helix transform enables three-dimensional post-stack migration processes that can process data for three-dimensional variations in velocity.[15] In addition, it can be applied to assist with the problem of implicit three-dimensional wavefield extrapolation.[16] Other applications include helpful algorithms in seismic data regularization, prediction error filters, and noise attenuation in geophysical digital systems.[14]Gaussian Convolution
One application of multidimensional convolution that is used within signal and image processing is Gaussian convolution. This refers to convolving an input signal with the Gaussian distribution function.The Gaussian distribution sampled at discrete values in one dimension is given by the following (assuming ):
Approximation by FIR Filter
Gaussian convolution can be effectively approximated via implementation of a Finite impulse response (FIR) filter. The filter will be designed with truncated versions of the Gaussian. For a two-dimensional filter, the transfer function of such a filter would be defined as the following:where
Choosing lower values for and will result in performing less computations, but will yield a less accurate approximation while choosing higher values will yield a more accurate approximation, but will require a greater number of computations.
Approximation by Box Filter
Another method for approximating Gaussian convolution is via recursive passes through a box filter. For approximating one-dimensional convolution, this filter is defined as the following:Typically, recursive passes 3, 4, or 5 times are performed in order to obtain an accurate approximation. A suggested method for computing r is then given as the following:
where K is the number of recursive passes through the filter.
Then, since the Gaussian distribution is separable across different dimensions, it follows that recursive passes through one-dimensional filters (isolating each dimension separately) will thus yield an approximation of the multidimensional Gaussian convolution. That is, M-dimensional Gaussian convolution could be approximated via recursive passes through the following one-dimensional filters:
Applications
Gaussian convolutions are used extensively in signal and image processing. For example, image-blurring can be accomplished with Gaussian convolution where the parameter will control the strength of the blurring. Higher values would thus correspond to a more blurry end result. It is also commonly used in Computer vision applications such as Scale-invariant feature transform (SIFT) feature detection.++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
MATH <---------> HTAM LJBUSAF
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

![X_{2\pi }(\omega )=\sum _{n=-\infty }^{\infty }x[n]\,e^{-i\omega n}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/b912dd8998ca4ec2d477f047c6aef79c6a55f317)
![T\cdot x(nT)=x[n]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca2ca9463d6b6da9fa9f28f0838eb87419b42d2)

![X_{1/T}(f)=X_{2\pi }(2\pi fT)\ {\stackrel {\mathrm {def} }{=}}\sum _{n=-\infty }^{\infty }\underbrace {T\cdot x(nT)} _{x[n]}\ e^{-i2\pi fTn}\;{\stackrel {\mathrm {Poisson\;f.} }{=}}\;\sum _{k=-\infty }^{\infty }X\left(f-k/T\right).](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff9b932cdb07bb87e03786d0705c557766d63f23)



![X_{1/T}(f)={\mathcal {F}}\left\{\sum _{n=-\infty }^{\infty }x[n]\cdot \delta (t-nT)\right\}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eff3beb99f3510f9a94ba158b21018f980a6c6a6)
![\sum _{n=-\infty }^{\infty }x[n]\cdot \delta (t-nT)={\mathcal {F}}^{-1}\left\{X_{1/T}(f)\right\}\ {\stackrel {\mathrm {def} }{=}}\int _{-\infty }^{\infty }X_{1/T}(f)\cdot e^{i2\pi ft}df.](https://wikimedia.org/api/rest_v1/media/math/render/svg/67126209df0c938694ada453169eb06f1cfd05a2)
![{\begin{aligned}x[n]&=T\int _{\frac {1}{T}}X_{1/T}(f)\cdot e^{i2\pi fnT}df\quad \scriptstyle {{\text{(integral over any interval of length }}1/T{\textrm {)}}}\\\displaystyle &={\frac {1}{2\pi }}\int _{2\pi }X_{2\pi }(\omega )\cdot e^{i\omega n}d\omega \quad \scriptstyle {{\text{(integral over any interval of length }}2\pi {\textrm {)}}}\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d020e6fa5917588e8c03e44a1632fcb5e1a5d4e7)



![\scriptstyle x[n]\cdot e^{-i2\pi fTn}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6d913a1d6c75370fd15f14292d9e6c556a0aba9)


![{\displaystyle {\begin{aligned}X_{1/T}\left({\frac {k}{NT}}\right)&=\sum _{m=-\infty }^{\infty }\left(\sum _{N}x[n-mN]\cdot e^{-i2\pi {\frac {k}{N}}(n-mN)}\right)\\&=\sum _{m=-\infty }^{\infty }\left(\sum _{N}x[n]\cdot e^{-i2\pi {\frac {k}{N}}n}\right)=T\underbrace {\left(\sum _{N}x(nT)\cdot e^{-i2\pi {\frac {k}{N}}n}\right)} _{X[k]\quad {\text{(DFT)}}}\cdot \left(\sum _{m=-\infty }^{\infty }1\right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a84925f9361a20a6398f62c0ceba71a9835570e)
![{\displaystyle X_{1/T}(f)=\sum _{k=-\infty }^{\infty }(T\cdot X[k])\ \cdot \ {\frac {1}{NT}}\delta \left(f-{\frac {k}{NT}}\right)=\underbrace {{\frac {1}{N}}\sum _{k=-\infty }^{\infty }X[k]\ \cdot \ \delta \left(f-{\frac {k}{NT}}\right)} _{\text{DTFT of a periodic sequence}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/84b47996e6c44906619e0274d6d241a3a3480f49)
![{\begin{aligned}\underbrace {X_{1/T}\left({\frac {k}{NT}}\right)} _{X_{k}}&=\sum _{n=-\infty }^{\infty }x[n]\cdot e^{-i2\pi {\frac {kn}{N}}}\quad \quad k=0,\dots ,N-1\\&=\underbrace {\sum _{N}x_{N}[n]\cdot e^{-i2\pi {\frac {kn}{N}}},} _{DFT}\quad \scriptstyle {{\text{(sum over any }}n{\text{-sequence of length }}N)}\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f28205b9e08c0a908dfa5739a9849eef8a4d93cd)
![x_{N}[n]\ {\stackrel {\text{def}}{=}}\ \sum _{m=-\infty }^{\infty }x[n-mN].](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b7896ba97a8a615b060c11a1944653ed45d02b0)


![X_{k}=\sum _{n=0}^{N-1}x[n]\cdot e^{-i2\pi {\frac {kn}{N}}}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd1a19c76a393d195cba26b8a7a7a4ccceb51207)
![x[n]=e^{i2\pi {\frac {1}{8}}n},\quad](https://wikimedia.org/api/rest_v1/media/math/render/svg/baae6124a1bf8d991adecc618048e7a52c92ae60)

![x*y\ =\ \scriptstyle {\text{DTFT}}^{-1}\displaystyle \left[\scriptstyle {\text{DTFT}}\displaystyle \{x\}\cdot \scriptstyle {\text{DTFT}}\displaystyle \{y\}\right].](https://wikimedia.org/api/rest_v1/media/math/render/svg/d44327e03ff8b9bfbafd6c9fc2b98e61a312ed88)
![x_{N}*y\ =\ \scriptstyle {\text{DTFT}}^{-1}\displaystyle \left[\scriptstyle {\text{DTFT}}\displaystyle \{x_{N}\}\cdot \scriptstyle {\text{DTFT}}\displaystyle \{y\}\right]\ =\ \scriptstyle {\text{DFT}}^{-1}\displaystyle \left[\scriptstyle {\text{DFT}}\displaystyle \{x_{N}\}\cdot \scriptstyle {\text{DFT}}\displaystyle \{y_{N}\}\right].](https://wikimedia.org/api/rest_v1/media/math/render/svg/54b615d9a29534372a1b12e46de9480992faded6)
![x_{N}*y\ =\ \scriptstyle {\text{DFT}}^{-1}\displaystyle \left[\scriptstyle {\text{DFT}}\displaystyle \{x\}\cdot \scriptstyle {\text{DFT}}\displaystyle \{y\}\right].](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f1b7d39bf27e8b1bf67983a7a8bb9da2158bae2)
![x[n]](https://wikimedia.org/api/rest_v1/media/math/render/svg/864cbbefbdcb55af4d9390911de1bf70167c4a3d)
![{\displaystyle x[n]\in \mathbb {R} \quad \forall n\in \mathbb {N} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c333eacb1eb403fe88946f375e0ea71cbfcea5c)

![{\displaystyle x[n]\in \mathbb {R} \quad \forall n\in \mathbb {N} \quad \Leftrightarrow \quad X_{2\pi }(\omega )={\overline {X_{2\pi }(-\omega )}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad15e36534ad7cdfeaf25c0d27f3531f15ae59f4)
![{\displaystyle x[n]={\overline {x[-n]}}\quad \forall n\in \mathbb {N} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/810f41dad89091a3a5144505142fe81e70e55eb8)

![{\displaystyle x[n]=-{\overline {x[-n]}}\quad \forall n\in \mathbb {N} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ed5179d9f667d0780c6d7f4f6128a0391690f4e)
![{\displaystyle \underbrace {{\mathcal {Z}}\{x[n]\}} _{{\widehat {X}}(z)}=\sum _{n=-\infty }^{\infty }x[n]\,z^{-n},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7eaf67cbd1bf8e55b9789334f115353510c2f325)

![{\displaystyle {\begin{aligned}{\widehat {X}}(e^{i\omega })&=\sum _{n=-\infty }^{\infty }x[n]\,e^{-i\omega n}\ =\ X_{2\pi }(\omega )\ =\ X_{1/T}\left({\tfrac {\omega }{2\pi T}}\right)\ =\ \sum _{k=-\infty }^{\infty }X\left({\tfrac {\omega }{2\pi T}}-k/T\right)\\&=\sum _{k=-\infty }^{\infty }X\left({\tfrac {\omega -2\pi k}{2\pi T}}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/43754694f1cfd21b0c313a52bdc28f65d61fb822)


![\delta [n]](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2a6caf535cb44fa3526b2f320330a805edfdfaa)

![\delta [n-M]](https://wikimedia.org/api/rest_v1/media/math/render/svg/cedaa6f1303f1a7d59626c2d10d2b3a0bbf33e14)

![\sum _{m=-\infty }^{\infty }\delta [n-Mm]\!](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e96f3a5de2797d89e30f9856c0da6683218f006)



![u[n]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6f1362207606428a09d907db25527859eab6ac3)



![a^{n}u[n]](https://wikimedia.org/api/rest_v1/media/math/render/svg/bef62e50254aa3175939a01611766c01f9bf7b39)






![{\displaystyle X_{o}(\omega )=\pi \left[\delta \left(\omega -a\right)+\delta \left(\omega +a\right)\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8000a8fe75a6c72eec0e0136ad92b765ab26c6a)


![{\displaystyle X_{o}(\omega )={\frac {\pi }{i}}\left[\delta \left(\omega -a\right)-\delta \left(\omega +a\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ad5113a293e183251175901267f2a272bb20d05)
![\operatorname {rect} \left[{n-M/2 \over M}\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/471edc79924f58eabe08b14df0142b02df94618e)
![{\displaystyle X_{o}(\omega )={\sin[\omega (M+1)/2] \over \sin(\omega /2)}\,e^{-{\frac {i\omega M}{2}}}\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad3e5f10d767ea8026153b3afb1428b04a647828)








![{\displaystyle {\frac {1}{(n+a)}}\left\{\cos[\pi W(n+a)]-\operatorname {sinc} [W(n+a)]\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ebaa12f993e5ff4ffcb48340c25ce6017a8ea85e)





![{\frac {C(A+B)}{2\pi }}\cdot \operatorname {sinc} \left[{\frac {A-B}{2\pi }}n\right]\cdot \operatorname {sinc} \left[{\frac {A+B}{2\pi }}n\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/38083aff1d4f22b4848dfafdc988b43142f7c472)


![{\displaystyle a\cdot x[n]+b\cdot y[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/268723a72269bb3e7b875ed4ee4061005ba9a105)

![x[n-k]](https://wikimedia.org/api/rest_v1/media/math/render/svg/4fd4fa5b96ade59fee1aa33657f28a6ed743fee0)

![{\displaystyle x[n]\cdot e^{ian}\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a8e4067c00fade9728fc479bd06a4ceee8a3db6)

![{\displaystyle x[nM]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0d6c2609310edf1b59b2e4dc43d4da977d66858)

![{\displaystyle \scriptstyle {\begin{cases}x[n/M]&n={\text{multiple of M}}\\0&{\text{otherwise}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b3ef4ee78f5eba71b905748c113a7158004c69a)

![x[-n]](https://wikimedia.org/api/rest_v1/media/math/render/svg/2958bd31d147e297b9544bac8ecb293bc64c54e2)

![{\displaystyle x[n]^{*}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/edad1abfdca495a8e9ecb60b39a6e79acf203073)

![{\displaystyle x[-n]^{*}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a69f14a67aa0f23b2bbc6b33206ae29bf68879d1)

![{\frac {n}{i}}x[n]\!](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2eb71af662480e119b9bd16ff2e4c49151ab4b9)

![{\displaystyle x[n]-x[n-1]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/109405d5524e374dc23cb716c5a696b5bca66010)

![x[n]*y[n]\!](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e3b1fd5ad225be66dfa022f43a3333b08fb3fb7)

![x[n]\cdot y[n]\!](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3e208ac041ff192194184d3c708d7789f9c9178)

![\rho _{xy}[n]=x[-n]^{*}*y[n]\!](https://wikimedia.org/api/rest_v1/media/math/render/svg/37d82c9624d4b16650c5652c000d0bb459f794c6)

![{\displaystyle E=\sum _{n=-\infty }^{\infty }{x[n]\cdot y[n]^{*}}\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f7ce039c5b6d271a19d5eb3bc40cef3ac810306)

















































![{\displaystyle {\begin{aligned}A_{m}(f)^{2}=\left[\sum _{i=-f}^{f}\right.&\operatorname {FFT} (-f,i)^{2}+\sum _{i=-f}^{f}\operatorname {FFT} (f,i)^{2}\\[5pt]&\left.{}+\sum _{i=-f+1}^{f-1}\operatorname {FFT} (i,-f)^{2}+\sum _{i=-f+1}^{f-1}\operatorname {FFT} (i,f)^{2}\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/65e2b7dace8996c89cce35132a4f1e451800a219)

















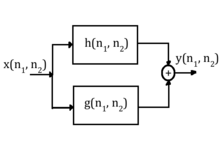




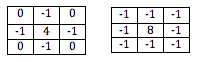







![x(n_1,n_2)**h(n_1,n_2)=\bigg[x(n_1)*h(n_1)\bigg]\bigg[x(n_2)*h(n_2)\bigg]](https://wikimedia.org/api/rest_v1/media/math/render/svg/f71c141b786fcce579b75251e82759f9cf61ec26)
![{\displaystyle x(n_{1},n_{2},...,n_{M})*{\overset {M}{\cdots }}*h(n_{1},n_{2},...,n_{M})={\bigg [}x(n_{1})*h(n_{2}){\bigg ]}{\bigg [}x(n_{2})*h(n_{2}){\bigg ]}...{\bigg [}x(n_{M})*h(n_{M}){\bigg ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd6a0ff642c93d8a3f920c8e8cf354e8bddbbaea)



![{\displaystyle y(n_{1},n_{2})=\sum _{k_{1}=-\infty }^{\infty }h_{1}(k_{1}){\Bigg [}\sum _{k_{2}=-\infty }^{\infty }h_{2}(k_{2})x(n_{1}-k_{1},n_{2}-k_{2}){\Bigg ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5880452f668f43ffe07acfc31401794e74ee793b)









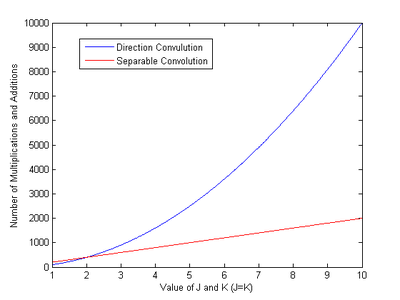




















![{\displaystyle y_{circular}(n_{1},n_{2})=\sum _{r_{1}}\sum _{r_{2}}{\Bigg [}\sum _{m_{1}=0}^{Q_{1}-1}\sum _{m_{2}=0}^{Q_{2}-1}h(m_{1},m_{2})x(n_{1}-m_{1}-r_{1}N_{1},n_{2}-m_{2}-r_{2}N_{2}){\Bigg ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b357fcd547e161addd82bb52a99ec6a92ef013e4)