Einstein’s time
It is now appropriate to concentrate on Einstein’s concept of “every time - absolute time”. Einstein could not explain his idea clearly, because wave theory — the main link between all energy theories — was unavailable to him. Despite this, using his genius and intuition, he introduced quantum physics, as well as the concept of speeds greater than light serving as bridges (wormholes). Einstein could not explain his feeling, and neither he nor anyone else had the courage to declare that energetic matter, which he introduced in the equation E = mc2, is the basis of all matter. At that time, there was no energetic matter theory; now, wave theory explains these ideas easily. Wave theory proves that there are speeds greater than light and all of Einstein’s ideas.
The behaviour of energetic matter allows all phases to coexist in the same space without disturbing one another. Only neighbouring phases influence one another.
Energy (energetic matter), space and time are one. Wave theory introduces energetic matter — a single inflationary force — as the main creation of nature. Energetic matter creates wave formations and they, in turn, create everything.
We all feel that time seems like an eternity when waiting for something when under pressure. In such a hectic (high energy) state, our brains consume more energy, thus prolonging time. Another example would be the minds of the young compared to those of the elderly. In the same period of time, the young, whose brains have larger energetic capacities, can absorb more information than the elderly. Both of these examples serve to illustrate Einstein’s concepts of time.
The behaviour of energetic matter allows all phases to coexist in the same space without disturbing one another. Only neighbouring phases influence one another.
Energy (energetic matter), space and time are one. Wave theory introduces energetic matter — a single inflationary force — as the main creation of nature. Energetic matter creates wave formations and they, in turn, create everything.
We all feel that time seems like an eternity when waiting for something when under pressure. In such a hectic (high energy) state, our brains consume more energy, thus prolonging time. Another example would be the minds of the young compared to those of the elderly. In the same period of time, the young, whose brains have larger energetic capacities, can absorb more information than the elderly. Both of these examples serve to illustrate Einstein’s concepts of time.
To understand the electron’s structure and behaviour, let us look at the pictures of the Whirlpool Galaxy, M51 and Stefan’s Quintet (N.G.C. 7137-20) galaxies (pictures below). These pictures help us to imagine the electron’s structure as one possible way of connecting energetic formations. For a greater understanding, see the galaxy drawings below.


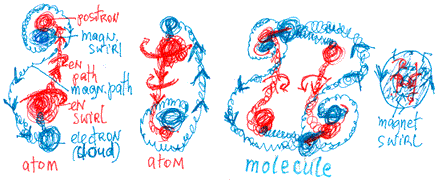
Cloud-like formations of energetic matter appear near the point at which the paths join the swirls. At the apex of the magnetic (Schwarzschild, A2) swirl, we see a tightly held cloud of energetic matter flowing toward it from the energetic (Kerr, A1) swirl. This cloud forms when the swirl cannot handle all the energy flowing to it. Energetic matter from the Schwarzschild swirl flows along a magnetic path and creates a more loosely held cloud of energetic matter near the confluence of the Kerr swirl.
Every energetic path is composed of magnetic and energetic rings, but the proportions and behaviour of the rings are different in each path. The energetic cloud is not static. It is a living formation of swirling and vibrating energetic matter. The cloud near the Kerr swirl rotates in a perpendicular direction, as does the magnetic loop. It is part of the magnetic paths and is very loosely connected to both the paths and to the swirl.
From beautiful pictures obtained of the sun, we see that energetic matter expelled from the star moves in the form of a swirl (picture below). This energetic path is probably mainly composed of magnetic loops, because the energetic loops that look like dark circles on the surface of the sun are composed of invisible energetic (dark) matter.

Before it is sucked into the Kerr swirl, the magnetic path creates a swirling cloud. Perhaps, in the atom, this formation is the electron (a moving cloud). The Kerr swirl, which behaves like a black hole, can swallow only small amounts of energy. Excess energy is concentrated near the mouth of the swirl and grows, achieving more mobility and space. In the atom, the electron cloud appears to be more independent and jumps to a higher orbit. Perhaps, rather than actually jumping to a higher orbit, the electron cloud enlarges its space enough to come in contact with the higher orbit.
The enlargement of the electron cloud’s space, caused by the addition of energy,  enables it to form relationships with swirls of other atoms. Because it is magnetic, it connects with positron loops near Schwarzschild swirls and creates a small photon-like wave (picture to the right). The cloud, however, does not lose contact with the matter from which it originated.
enables it to form relationships with swirls of other atoms. Because it is magnetic, it connects with positron loops near Schwarzschild swirls and creates a small photon-like wave (picture to the right). The cloud, however, does not lose contact with the matter from which it originated.
 enables it to form relationships with swirls of other atoms. Because it is magnetic, it connects with positron loops near Schwarzschild swirls and creates a small photon-like wave (picture to the right). The cloud, however, does not lose contact with the matter from which it originated.
enables it to form relationships with swirls of other atoms. Because it is magnetic, it connects with positron loops near Schwarzschild swirls and creates a small photon-like wave (picture to the right). The cloud, however, does not lose contact with the matter from which it originated.
Because the electron cloud belongs to the magnetic path (picture below), it moves in  a perpendicular path from north to south or south to north, or around the energetic swirl (proton) - but only in the direction of the swirl’s rotation, west to east. This is the rotation of atomic energy formations.
a perpendicular path from north to south or south to north, or around the energetic swirl (proton) - but only in the direction of the swirl’s rotation, west to east. This is the rotation of atomic energy formations.
 a perpendicular path from north to south or south to north, or around the energetic swirl (proton) - but only in the direction of the swirl’s rotation, west to east. This is the rotation of atomic energy formations.
a perpendicular path from north to south or south to north, or around the energetic swirl (proton) - but only in the direction of the swirl’s rotation, west to east. This is the rotation of atomic energy formations.
By adding more energy, the electron cloud can separate itself from its wave and become a high-energy independent magnetic loop (electron), flowing between atoms in the energetic path. Once the atom from which the electron originated creates another cloud of excess energy, the lost electron cannot return to its original wave. If it is connected to magnetic paths, the electron can jump orbits when energy is added, and return to its original size when energy is lost. Every atom has its specific energy level, space and time. When energy is added, their orbits cannot exceed the energy level of the original wave. Excess energy is expelled in the form of photons bearing the characteristics of the atom releasing them.
Every electron has its own space, spin, momentum and mass (interaction between energetic formations), and is a high-energy, independent formation. As its  behaviour is derived from the Schwarzschild swirl, so its rotation is like the vertical, magnetic loop of a wave (see the chapter on quarks). The electron’s polarity is negative; this differs from the energetic swirl and path (picture right).
behaviour is derived from the Schwarzschild swirl, so its rotation is like the vertical, magnetic loop of a wave (see the chapter on quarks). The electron’s polarity is negative; this differs from the energetic swirl and path (picture right).
 behaviour is derived from the Schwarzschild swirl, so its rotation is like the vertical, magnetic loop of a wave (see the chapter on quarks). The electron’s polarity is negative; this differs from the energetic swirl and path (picture right).
behaviour is derived from the Schwarzschild swirl, so its rotation is like the vertical, magnetic loop of a wave (see the chapter on quarks). The electron’s polarity is negative; this differs from the energetic swirl and path (picture right).
In front of the magnetic swirl is a positron: a concentrated swirl of energetic matter from the energetic swirl, having a horizontal plane of rotation. When an electron (a swirl with magnetic properties) collides with a positron, a high-energy wave (photon) is formed (picture below).

In molecules, however, the connection between the positron and the electron appears like a wave formation, and magnetic energy from both atoms circulates as one magnetic swirl in the molecule’s space.
Electricity is the movement of energetic matter in wires around the surface of electrons (magnetic loops). The electrons cannot handle the excess energy, and so the energy continues to move onward. The electron is not a static object rotating around a proton (energetic swirl), but a living formation, constantly changing position and energy levels. As stated by Feynman, orbit changes are very characteristic of electrons. Energy loss in atoms occurs mainly through electrons (vibration).
The nucleus of the atom is composed of photon-like structures strongly connected by their energetic loops (picture, near right). The connection between atoms and  molecules is the result of the electron (picture, far right): an energetic condensate cloud in front of the energetic swirl, waiting to be swallowed by it. The swirl slowly melts the matter until a singularity is formed, which ejects the energy. The energy becomes a magnetic loop that, in turn, creates another electron cloud of condensate energetic matter.
molecules is the result of the electron (picture, far right): an energetic condensate cloud in front of the energetic swirl, waiting to be swallowed by it. The swirl slowly melts the matter until a singularity is formed, which ejects the energy. The energy becomes a magnetic loop that, in turn, creates another electron cloud of condensate energetic matter.
 molecules is the result of the electron (picture, far right): an energetic condensate cloud in front of the energetic swirl, waiting to be swallowed by it. The swirl slowly melts the matter until a singularity is formed, which ejects the energy. The energy becomes a magnetic loop that, in turn, creates another electron cloud of condensate energetic matter.
molecules is the result of the electron (picture, far right): an energetic condensate cloud in front of the energetic swirl, waiting to be swallowed by it. The swirl slowly melts the matter until a singularity is formed, which ejects the energy. The energy becomes a magnetic loop that, in turn, creates another electron cloud of condensate energetic matter.
Every addition of energy enlarges the cloud, but not the swirl, which cannot exceed its original size. The electron can thus come into contact with other swirls or jump orbits (temporarily enlarge its space).
Disconnecting atoms and molecules occurs by adding energy and enlarging the magnetic path connecting the electron. In strong magnetic fields, one atom of a molecule travels to the north pole of a magnet and a second travels to the south. It is very important to understand molecular bonds. In the first picture on this page, the A2 molecules travel to opposite magnetic poles, demonstrating that they have different directions of rotation.
Disconnecting atoms and molecules occurs by adding energy and enlarging the magnetic path connecting the electron. In strong magnetic fields, one atom of a molecule travels to the north pole of a magnet and a second travels to the south. It is very important to understand molecular bonds. In the first picture on this page, the A2 molecules travel to opposite magnetic poles, demonstrating that they have different directions of rotation.
Atoms in molecules rotate in opposite directions. The theoretical structure of molecules is a very complex energetic matter bond. The most important bonds between atoms and molecules are by electrons, the most mobile formation in the atom. By adding energy it can extend its space and easily come in contact with a positron and create a wave formation (positron + electron = electro-magnetic wave). The wave from two high-energy formations is high-energy. It can be separated by adding energy or by a lack of energy, as occurs in organic formations. A hydrogen electron in organic bonds, with its large radius, is very sensitive to downward energy shifts that decrease its size. In the sodium atom, the second level photon is large and the electron has a large radius that easily creates molecular bounds.
In the atom, bonding is carried out by energetic loops. We see clearly that their pulling forces maintain the structure, while the pushing forces of magnetic loops weaken it. In molecules, where bonding is by magnetic electron swirls, the structure is weaker and needs more energy to maintain it . Distances between atoms (waves) in a molecule are larger than between photons (waves) in the atom’s nucleus; they can easily be separated or joined.
Molecular bonds create energetic swirls between and around atoms. In astronomical observations of celestial clusters, we see similar formations that resemble beehives.
Energetic matters’ behaviour is the same in formations of all sizes. Energy circulation in all objects must be executed by wave formations. It is sometimes very difficult to find a wave formation in an object, but by careful observation we may do so. Molecule Bonds
Single energy formations like atoms must join others to create a closed swirl formation that is capable of stabilizing energy. In this formation, in addition to the each atom’s individual swirl, there is a common central swirl that maintains energy in a stronger fashion than the single atoms did. These central swirls can be highly energetic, as in atoms, or weakly magnetic, as in molecules. Every closed formation has one purpose: to maintain energy, which is inflationary and tries to escape into space. The following picture shows the molecule connections:
From this picture, we see that adding energy elongates the magnetic path and enlarge the space between the electron and the energetic swirl. The electron cloud comes in contact with the positron cloud in front of the magnetic swirl of a neighbouring atom, creating a large, high-energy positron-electron wave-like formation. By adding energy, the electron can be easily separated from the positron of the second atom; the electron will not, however, escape from its own atom. An enormous amount of energy is required to enlarge the electron’s space and enable it to escape the atom’s wave.
Every atom must gather its characteristic requirement of energy to jump to a new orbit. This orbit is a new, fluctuating energetic path, connected by double paths to the magnetic and energetic swirls.
Life
The following pictures are worth a thousand words:


The essential matter from which our universe is created is energetic matter. It behaves like living matter, creating every known entity, including living objects and even thought (which occurs through energetic matter–wave interaction). The 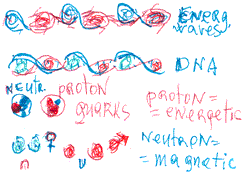 essential structure of energetic matter is high-energy (concentrated energetic matter) electro-magnetic waves (picture above). This simple structure is the basis of everything: every energetic formation and the universe. In picture 2, we see that the DNA (double helix) of all living formations has the same structure as waves: two loops of the same energetic matter, behaving according to the same rules.
essential structure of energetic matter is high-energy (concentrated energetic matter) electro-magnetic waves (picture above). This simple structure is the basis of everything: every energetic formation and the universe. In picture 2, we see that the DNA (double helix) of all living formations has the same structure as waves: two loops of the same energetic matter, behaving according to the same rules.
 essential structure of energetic matter is high-energy (concentrated energetic matter) electro-magnetic waves (picture above). This simple structure is the basis of everything: every energetic formation and the universe. In picture 2, we see that the DNA (double helix) of all living formations has the same structure as waves: two loops of the same energetic matter, behaving according to the same rules.
essential structure of energetic matter is high-energy (concentrated energetic matter) electro-magnetic waves (picture above). This simple structure is the basis of everything: every energetic formation and the universe. In picture 2, we see that the DNA (double helix) of all living formations has the same structure as waves: two loops of the same energetic matter, behaving according to the same rules.
In this chapter, I will discuss biological, living beings in terms of chemistry and physics, since basic energetic matter creates everything. The existence of living objects entails many substances. The main components, however, of energetic waves and basic atoms are hydrogen, carbon, nitrogen and oxygen. This applies to other atoms, as well. Life is not an accidental event. Where methane, ethane, propane and other similar compounds are present, organic creations can easily be created without further assistance. Carbon atoms are plentiful in all energetic formations, even young galaxies. Hydrogen atoms were one of the first creations, before other atoms, and are widespread in the universe. Where there are two main components such as hydrogen and carbon, chemical compounds, which are the basis of high-energy bonds, can be created.
The most important formations for life (see picture, below left) are cyclohexane-like bonds, which are energetic closed swirl formations. They contain a great deal of energy and resemble the Young Star Clusters Stud NGC 1512 (picture, below right).


Those structures, similar to the star cluster stud, are the basis for life formations. DNA, like waves, has a large energetic capacity, which makes living formations independent of their surroundings. Both can store energy in internal swirls by different methods and can communicate with other wave formations.
The formation of DNA, with two loops and two swirls, clearly resembles cosmic waves in which one swirl is energetic and the second is more magnetic.
In humans, a female’s ovum resembles the formation of a young star cluster. Similar to the properties of magnetic loops, it is capable of storing a great deal of energy. When united with the sperm, which is a high-energy formation (like an energetic loop), a stable wave-like formation is created. The need to procreate is one reason that sex is a basic human drive. The first energetic formations are two loops - one stable wave formation. This is one of the ingenious formations of energetic matter, as it enables the interchange of energetic information between waves and all other energetic formations in the universe.
These two loops are in perpetual competition and cannot exist without one another (see the chapter on photons). This allows us to understand the sexual behaviour of all species.
In the chapter on photons, we noted that in order to separate photon loops, there has to be some energy added to its formation. In the reverse process, excess energy is expelled in the form of a photon. The same process occurs in nature. When the magnetic loop (the ovum) meets the energetic loop (the sperm), the outcome is the formation of a new, high-energy photon-like creation, which has genes (time, space) containing complete information from previous formations.
As oxygen and hydrogen are plentiful everywhere in the universe, the creation of water readily occurs. Theories about life in water are well known. Energy discharges, as from lightning, may help to form organic bonds that create simple organic formations.
Wave theory suggests that inorganic and organic creations are one entity of nature (see picture, below). Perhaps, the result of the energetic activity of hydrogen and oxygen creates water on our planet. It may be that the Earth alone can continuously create life formations. This process is very delicate and may be easily spoilt. Nature has worked for millions of years to generate the myriad of links in this symbiosis. We must try not to change this unbelievable, beautiful, ingenious creation, but must only attempt to discover, study and appreciate it. Energetic matter creates structures beyond our imagination; our planet is, perhaps, only one of these creations. On other planets, living formations may have other shapes.

I will not continue this discussion now, but will try to do so in other essays. Water, atmosphere and life are very complex issues and strongly connected. Nature and our environment should be respected and protected by all mankind.
Four main elements, hydrogen, carbon, oxygen and nitrogen, are essential in the creation of living formations. The most vital is carbon. With its high heat of vaporization of kJ/mol ~ 715, it is very stable. Water also has a high heat of vaporization: kJ/ mol ~ 539.
Hydrogen has a high-energy “electron” capacity and the largest atomic radius - 208i - among light atoms. Thus, the radius of energetic matter around this atom is very large and it connects easily with other atoms, which provides it with a great deal of energetic matter. It may be that peripheral periatomic energetic matter is van der Waals forces. Energetic matter is very important for vital formations because it is very sensitive to change occurring in neighbouring formations. The van der Waals forces come in contact with surrounding organic energy formations, which enables the easy and direct transfer of signals from one formation to another. The energy nets created between waves, atoms and molecules may be vital to life formation, as contact between energetic matter formations is the source of life.
A hydrogen atom consists of a nucleus and a high-energy loop-like electron. The nucleus behaves like a high-energy vortex (swirl) and the electron acts like a high-energy cloud, which easily initiates relationships with other high-energy atoms and organic bonds. This occurs mainly through hydrogen high-energy atom waves, easily supplied by water molecules.
An independent living formation has more energy than its surroundings and has organs to utilize its energy and store it for generations. Its “genes” have the ability to reproduce these behaviours and qualities, so that the formation keeps its energetic matter formation.
Organic living formations
Organic living formations contain a great deal of energy, making them independent of their surroundings. To maintain a high energy level (capacity), they require a continuous supply of energy. To this end, the molecules bond with similar molecules and then differentiate, generating organelle that obtain energy from their surroundings. Thus, an organic living formation appears and continually improves its energy utilization to survive.
Organic living formations contain a great deal of energy, making them independent of their surroundings. To maintain a high energy level (capacity), they require a continuous supply of energy. To this end, the molecules bond with similar molecules and then differentiate, generating organelle that obtain energy from their surroundings. Thus, an organic living formation appears and continually improves its energy utilization to survive.
This process is part of the natural creation continuum. We noted in the chapters on photons and quarks that energy constantly tries to escape from a wave structure, while magnetic rings try to retain energy to maintain the wave’s space and independence. The same behaviour leads to the creation of an organic living formation with a high-energy capacity, which takes as much energy as possible from its surroundings to remain independent.
We believe that communication between different organelle occurs mainly in chemical, physical and mechanical ways. It seems to me, however, that an additional important way for energy signal exchange is through energetic matter and its space. This is what gives chemical and physical connections their virtual relationship.
The high-energy hydrogen vortex is the basis for life everywhere. The hydrogen in water molecules H-O-H creates a high-energy compound with oxygen, which can transfer energy matter from one source to another. High-energy water molecules are a source of living formations. With constantly moving molecules (Brownian motion), water helps supply energy from its surroundings to living formations, which utilize this energy with new molecules of water. Life appears not only in water, but also in other high-energy liquids where different energy and organelle formations can easily communicate with each other. Every living formation is an energetic matter formation.
In the atom, the proton (energetic vortex) is the highest energy formation (core of the atom). With the help of the electron, its energetic swirl transmits excess energy to living organisms in its surroundings. To sustain their existence, living creations constantly need the energy supplied by fresh water; its high-energy atoms give and receive energy from the surroundings. The main source of energy for living formations, however, is derived from the sun, but other sources are also available. As the Earth decays, it disperses energy. In the future, this may be an important source of energy for humanity.
Our brains are surrounded by a great deal of water in constant circulation, and are hermetically closed, except for a connection to the spine enabling the exchange of the previous supply with fresh water. Virtual energy waves are supplied not only by oxygen energy in the blood stream, but also by water energy.
Water itself is a life formation; therefore, it is in constant motion. The Brownian motion of water molecules indicates that it is in perpetual energetic activity. Through its electron enlarged paths and virtual hydrogen and oxygen van der Waals forces, signals transmitted by energetic matter are exchanged between atoms, molecules and even other energy formations.
The high percentage of water in the world (70%) and the atmosphere constantly communicate, thereby maintaining the stable temperature vital for life and preventing a drastic change of energy. Carbon’s high-energy capacity (its heat of vaporization is ~715 kJ/mol) helps guard the stable temperature of organic bonds.
Water, with its high-energy capacity, has an adhesive property, which means it creates common paths with other atoms. Hydrogen, oxygen, carbon and nitrogen are highly energetic, have large electron paths and strong van der Waals forces (periatomic energetic matter, plasma) and easily link to one another. Liquid energy sources enhance this ability. Forces surrounding organic formations also facilitate the transfer of signals between them.
As energetic paths of hydrogen are larger, it is easier to create vibration links (relationships) with other carbon hydrogen energetic paths. By a change of energetic activity (path vibration), energetic matter transfers messages (energetic matter signals) and impulses between waves. The best communication is between waves and is most efficient when it occurs in the same energetic capacity path, radius and frequency.
To continually preserve and enlarge their energetic capacity and size (energetic matter, radii, bonds), living objects need a continuous supply of external energy. These living links exist because of the energy they receive from their surroundings. Thus appears a living formation that is more energetic than its surroundings and independent of them.
Van der Waals forces, together with chemical and physical connections, help link different waves, which create colonies of relationships between different organelle for the utilization of external energy or the distribution of energy. These colonies, with their organelle, create viruses, living cells like bacteria, and active objects that at a later stage of evolution may have to create different organisms. Darwin and others describe this beautifully.
Lack of energy supplements damages energetic matter paths, bonds and relationships. If this continues for a long period of time, there is a cessation of relationships between those organic bonds. If the supply of energy is not resumed before the critical time, the new bonds appearing between organic molecules are not on the same paths (links) and do not have the same relationships. This is what occurs in the event of a cerebral stroke.
As previously mentioned, water and other liquids are the most crucial media for life, due to their high-energy capacity and the assistance that they extend to energetic paths-bonds. Energy signals from external organic formations reach dedicated sites in the brain through energetic paths (nerves).

The signals are sent from the brain, by motor neurons, to different organisms, which return them by sensory nerve  paths. This process creates a closed energy cycle. These paths may be formed by organic bonds (coils), as in chromosomes (picture, right).
paths. This process creates a closed energy cycle. These paths may be formed by organic bonds (coils), as in chromosomes (picture, right).
 paths. This process creates a closed energy cycle. These paths may be formed by organic bonds (coils), as in chromosomes (picture, right).
paths. This process creates a closed energy cycle. These paths may be formed by organic bonds (coils), as in chromosomes (picture, right).
Although signal transfer via organic formations is very complicated, I have simplified the matter in order to stress that energetic matter is the primal matter that creates everything and directs all energetic activity in living formations.
Wave energy activity is more visible in primary organic formations, where energetic stimulation causes a reaction to all organelles. It was once believed that it is impossible to understand human thought. Now we see that brain waves and neurons are a key to understanding life formations.
The actions of energy waves are capable of being explained with more clarity (see picture to the right).  From pictures obtained by positron emission tomography , we see that energetic stimulation increases blood circulation and disperses energy to the brain in the form of a wave that is composed of both an energetic (red) and magnetic (blue) loop. They circulate around the brain until they find the setting suitable to its formation.
From pictures obtained by positron emission tomography , we see that energetic stimulation increases blood circulation and disperses energy to the brain in the form of a wave that is composed of both an energetic (red) and magnetic (blue) loop. They circulate around the brain until they find the setting suitable to its formation.
 From pictures obtained by positron emission tomography , we see that energetic stimulation increases blood circulation and disperses energy to the brain in the form of a wave that is composed of both an energetic (red) and magnetic (blue) loop. They circulate around the brain until they find the setting suitable to its formation.
From pictures obtained by positron emission tomography , we see that energetic stimulation increases blood circulation and disperses energy to the brain in the form of a wave that is composed of both an energetic (red) and magnetic (blue) loop. They circulate around the brain until they find the setting suitable to its formation.
Research into brain waves has inspired the paradigm for wave relationships of living formations. This is the beginning of an explanation for the basic process that controls life. Energetic matter itself behaves like living matter. It is no wonder that it can create endless life creations, beyond our imagination. This occurs mainly where extended waves of atomic bonds come in contact with each other and create common energetic paths, with common interests.
Electro-convulsive therapy may explain some energetic processes that occur in the brain. Approximately fifteen years ago, this technique was developed using three magnetic stimulations to stimulate brain motor circuits and test their integrity after the brain or spinal cord incurred damage. This technique was used as therapy and to look at how the brain controls different types of behaviour. With a tweak of the settings, brain activity is stimulated, even raising or depressing specific areas of the brain, which we see in the form of large synchronized electro-magnetic waves. We know that electro-magnetic pulses control the heart (picture below); they are the largest synchronized energy waves on an electrocardiogram.
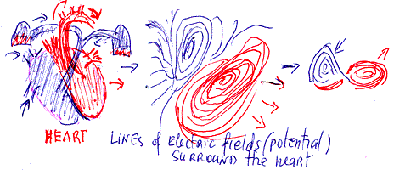
The oscillator, electrocardiogram and other devices help us understand and diagnose the function of living organs. Electro-magnetic waves are a result of an organ’s activity. Wave theory claims that energetic matter is the essential formation that creates everything, including living organs. Every living organ is a consequence of an infinite number of wave compositions, which matched until the organ was created. The waves we see in electronic devices are composites of all the organ’s inner waves. In the future, using different electronic devices and advanced technology, we may be able to locate and repair organs that do not function properly.
When observing our sun, we see that from time to time energetic matter is expelled, and that its movement is likely to be in a screw-spiral mode (picture, below).

The cerebral gyri (folding) of grey matter in the brain also have a screw-spiral mode. Every moving energy signal thus can easily match itself with a suitable gyrate brain formation. The brain has many different gyrate formations; therefore, it can receive different signals (energetic wave formations) and relay them to suitable gyri. In addition, the brain enhances chemical or physical relationships by sending energy impulses to other formations through its neuron roots.
It is clear why the brain uses as much as one quarter of the body’s energy to function well. The organ first visible in an embryo is the brain. Every living organism has a central energetic formation regulating the entire organism in different energetic ways. The brain’s basic structure is an example of the activity of energetic matter; DNA is an example of its wave formation (picture below). Every amino acid has a formation similar to a wave formation, as it contains a great deal of energy, like energetic swirls and their closed wave structures.

An ordinary wave, from its inception until its decay, cannot grow. It can only change phases. Living formations, however, continually swallow energy to stay strong and survive. In nature, stronger waves swallow weaker ones. The same phenomenon occurs when organic creations adapt to the use of external energy, which makes them independent of their surroundings, enables them to defend themselves and prolong their existence.
I began working on this “everything” theory roughly fifty years ago. Then, it was virtual; today, as I look at the research that has been done it seems real. Every day, mysterious energetic matter and its ability to create fascinate me more and more. I hope humanity will exploit it only for good.
Wave Theory is not the final theory. Energetic Space Theory is still waiting.
XXX . XXX zero null 0 1 2
The vacuum of space

Vacuum is space devoid of matter. The word stems from the Latin adjective vacuus for "vacant" or "void". An approximation to such vacuum is a region with a gaseous pressure much less than atmospheric pressure.[1] Physicists often discuss ideal test results that would occur in a perfect vacuum, which they sometimes simply call "vacuum" or free space, and use the term partial vacuum to refer to an actual imperfect vacuum as one might have in a laboratory or in space. In engineering and applied physics on the other hand, vacuum refers to any space in which the pressure is lower than atmospheric pressure.[2] The Latin term in vacuo is used to describe an object that is surrounded by a vacuum.
The quality of a partial vacuum refers to how closely it approaches a perfect vacuum. Other things equal, lower gas pressure means higher-quality vacuum. For example, a typical vacuum cleaner produces enough suction to reduce air pressure by around 20%.[3] Much higher-quality vacuums are possible. Ultra-high vacuum chambers, common in chemistry, physics, and engineering, operate below one trillionth (10−12) of atmospheric pressure (100 nPa), and can reach around 100 particles/cm3.[4] Outer space is an even higher-quality vacuum, with the equivalent of just a few hydrogen atoms per cubic meter on average.[5] According to modern understanding, even if all matter could be removed from a volume, it would still not be "empty" due to vacuum fluctuations, dark energy, transiting gamma rays, cosmic rays, neutrinos, and other phenomena in quantum physics. In the study of electromagnetism in the 19th century, vacuum was thought to be filled with a medium called aether. In modern particle physics, the vacuum state is considered the ground state of a field.
Vacuum has been a frequent topic of philosophical debate since ancient Greek times, but was not studied empirically until the 17th century. Evangelista Torricelli produced the first laboratory vacuum in 1643, and other experimental techniques were developed as a result of his theories of atmospheric pressure. A torricellian vacuum is created by filling a tall glass container closed at one end with mercury, and then inverting the container into a bowl to contain the mercury.[6]
Vacuum became a valuable industrial tool in the 20th century with the introduction of incandescent light bulbs and vacuum tubes, and a wide array of vacuum technology has since become available. The recent development of human spaceflight has raised interest in the impact of vacuum on human health, and on life forms in general.

there has been much dispute over whether such a thing as a vacuum can exist. Ancient Greek philosophers debated the existence of a vacuum, or void, in the context of atomism, which posited void and atom as the fundamental explanatory elements of physics. Following Plato, even the abstract concept of a featureless void faced considerable skepticism: it could not be apprehended by the senses, it could not, itself, provide additional explanatory power beyond the physical volume with which it was commensurate and, by definition, it was quite literally nothing at all, which cannot rightly be said to exist. Aristotle believed that no void could occur naturally, because the denser surrounding material continuum would immediately fill any incipient rarity that might give rise to a void.
In his Physics, book IV, Aristotle offered numerous arguments against the void: for example, that motion through a medium which offered no impediment could continue ad infinitum, there being no reason that something would come to rest anywhere in particular. Although Lucretius argued for the existence of vacuum in the first century BC and Hero of Alexandria tried unsuccessfully to create an artificial vacuum in the first century AD,[8] it was European scholars such as Roger Bacon, Blasius of Parma and Walter Burley in the 13th and 14th century who focused considerable attention on these issues. Eventually following Stoic physics in this instance, scholars from the 14th century onward increasingly departed from the Aristotelian perspective in favor of a supernatural void beyond the confines of the cosmos itself, a conclusion widely acknowledged by the 17th century, which helped to segregate natural and theological concerns.[9]
Almost two thousand years after Plato, René Descartes also proposed a geometrically based alternative theory of atomism, without the problematic nothing–everything dichotomy of void and atom. Although Descartes agreed with the contemporary position, that a vacuum does not occur in nature, the success of his namesake coordinate system and more implicitly, the spatial–corporeal component of his metaphysics would come to define the philosophically modern notion of empty space as a quantified extension of volume. By the ancient definition however, directional information and magnitude were conceptually distinct. With the acquiescence of Cartesian mechanical philosophy to the "brute fact" of action at a distance, and at length, its successful reification by force fields and ever more sophisticated geometric structure, the anachronism of empty space widened until "a seething ferment"[10] of quantum activity in the 20th century filled the vacuum with a virtual pleroma.
The explanation of a clepsydra or water clock was a popular topic in the Middle Ages. Although a simple wine skin sufficed to demonstrate a partial vacuum, in principle, more advanced suction pumps had been developed in Roman Pompeii.[11]
In the medieval Middle Eastern world, the physicist and Islamic scholar, Al-Farabi (Alpharabius, 872–950), conducted a small experiment concerning the existence of vacuum, in which he investigated handheld plungers in water.[12][unreliable source?] He concluded that air's volume can expand to fill available space, and he suggested that the concept of perfect vacuum was incoherent.[13] However, according to Nader El-Bizri, the physicist Ibn al-Haytham (Alhazen, 965–1039) and the Mu'tazili theologians disagreed with Aristotle and Al-Farabi, and they supported the existence of a void. Using geometry, Ibn al-Haytham mathematically demonstrated that place (al-makan) is the imagined three-dimensional void between the inner surfaces of a containing body.[14] According to Ahmad Dallal, Abū Rayhān al-Bīrūnī also states that "there is no observable evidence that rules out the possibility of vacuum".[15] The suction pump later appeared in Europe from the 15th century.[16][17][18]
Medieval thought experiments into the idea of a vacuum considered whether a vacuum was present, if only for an instant, between two flat plates when they were rapidly separated.[19] There was much discussion of whether the air moved in quickly enough as the plates were separated, or, as Walter Burley postulated, whether a 'celestial agent' prevented the vacuum arising. The commonly held view that nature abhorred a vacuum was called horror vacui. Speculation that even God could not create a vacuum if he wanted to was shut down[clarification needed] by the 1277 Paris condemnations of Bishop Etienne Tempier, which required there to be no restrictions on the powers of God, which led to the conclusion that God could create a vacuum if he so wished.[20]Jean Buridan reported in the 14th century that teams of ten horses could not pull open bellows when the port was sealed.[8]
The 17th century saw the first attempts to quantify measurements of partial vacuum.[21] Evangelista Torricelli's mercury barometer of 1643 and Blaise Pascal's experiments both demonstrated a partial vacuum.
In 1654, Otto von Guericke invented the first vacuum pump[22] and conducted his famous Magdeburg hemispheres experiment, showing that teams of horses could not separate two hemispheres from which the air had been partially evacuated. Robert Boyle improved Guericke's design and with the help of Robert Hooke further developed vacuum pump technology. Thereafter, research into the partial vacuum lapsed until 1850 when August Toepler invented the Toepler Pump and Heinrich Geissler invented the mercury displacement pump in 1855, achieving a partial vacuum of about 10 Pa (0.1 Torr). A number of electrical properties become observable at this vacuum level, which renewed interest in further research.
While outer space provides the most rarefied example of a naturally occurring partial vacuum, the heavens were originally thought to be seamlessly filled by a rigid indestructible material called aether. Borrowing somewhat from the pneuma of Stoic physics, aether came to be regarded as the rarefied air from which it took its name, (see Aether (mythology)). Early theories of light posited a ubiquitous terrestrial and celestial medium through which light propagated. Additionally, the concept informed Isaac Newton's explanations of both refraction and of radiant heat.[23] 19th century experiments into this luminiferous aether attempted to detect a minute drag on the Earth's orbit. While the Earth does, in fact, move through a relatively dense medium in comparison to that of interstellar space, the drag is so minuscule that it could not be detected. In 1912, astronomer Henry Pickering commented: "While the interstellar absorbing medium may be simply the ether, [it] is characteristic of a gas, and free gaseous molecules are certainly there".[24]
Later, in 1930, Paul Dirac proposed a model of the vacuum as an infinite sea of particles possessing negative energy, called the Dirac sea. This theory helped refine the predictions of his earlier formulated Dirac equation, and successfully predicted the existence of the positron, confirmed two years later. Werner Heisenberg's uncertainty principle formulated in 1927, predict a fundamental limit within which instantaneous position and momentum, or energy and time can be measured. This has far reaching consequences on the "emptiness" of space between particles. In the late 20th century, so-called virtual particles that arise spontaneously from empty space were confirmed.
Classical field theories The strictest criterion to define a vacuum is a region of space and time where all the components of the stress–energy tensor are zero. It means that this region is empty of energy and momentum, and by consequence, it must be empty of particles and other physical fields (such as electromagnetism) that contain energy and momentum.
Gravity
In general relativity, a vanishing stress-energy tensor implies, through Einstein field equations, the vanishing of all the components of the Ricci tensor. Vacuum does not mean that the curvature of space-time is necessarily flat: the gravitational field can still produce curvature in a vacuum in the form of tidal forces and gravitational waves (technically, these phenomena are the components of the Weyl tensor). The black hole (with zero electric charge) is an elegant example of a region completely "filled" with vacuum, but still showing a strong curvature.
Electromagnetism
In classical electromagnetism, the vacuum of free space, or sometimes just free space or perfect vacuum, is a standard reference medium for electromagnetic effects.[25][26] Some authors refer to this reference medium as classical vacuum,[25] a terminology intended to separate this concept from QED vacuum or QCD vacuum, where vacuum fluctuations can produce transient virtual particle densities and a relative permittivity and relative permeability that are not identically unity.[27][28][29]
In the theory of classical electromagnetism, free space has the following properties:
- Electromagnetic radiation travels, when unobstructed, at the speed of light, the defined value 299,792,458 m/s in SI units.[30]
- The superposition principle is always exactly true.[31] For example, the electric potential generated by two charges is the simple addition of the potentials generated by each charge in isolation. The value of the electric field at any point around these two charges is found by calculating the vector sum of the two electric fields from each of the charges acting alone.
- The permittivity and permeability are exactly the electric constant ε0[32] and magnetic constant μ0,[33] respectively (in SI units), or exactly 1 (in Gaussian units).
- The characteristic impedance (η) equals the impedance of free space Z0 ≈ 376.73 Ω.[34]
The vacuum of classical electromagnetism can be viewed as an idealized electromagnetic medium with the constitutive relations in SI units:[35]
relating the electric displacement field D to the electric field E and the magnetic field or H-field H to the magnetic induction or B-field B. Here r is a spatial location and t is time.
Quantum mechanics
In quantum mechanics and quantum field theory, the vacuum is defined as the state (that is, the solution to the equations of the theory) with the lowest possible energy (the ground state of the Hilbert space). In quantum electrodynamics this vacuum is referred to as 'QED vacuum' to distinguish it from the vacuum of quantum chromodynamics, denoted as QCD vacuum. QED vacuum is a state with no matter particles (hence the name), and also no photons. As described above, this state is impossible to achieve experimentally. (Even if every matter particle could somehow be removed from a volume, it would be impossible to eliminate all the blackbody photons.) Nonetheless, it provides a good model for realizable vacuum, and agrees with a number of experimental observations as described next.
QED vacuum has interesting and complex properties. In QED vacuum, the electric and magnetic fields have zero average values, but their variances are not zero.[36] As a result, QED vacuum contains vacuum fluctuations (virtual particles that hop into and out of existence), and a finite energy called vacuum energy. Vacuum fluctuations are an essential and ubiquitous part of quantum field theory. Some experimentally verified effects of vacuum fluctuations include spontaneous emission and the Lamb shift.[20] Coulomb's law and the electric potential in vacuum near an electric charge are modified.[37]
Theoretically, in QCD multiple vacuum states can coexist.[38] The starting and ending of cosmological inflation is thought to have arisen from transitions between different vacuum states. For theories obtained by quantization of a classical theory, each stationary point of the energy in the configuration space gives rise to a single vacuum. String theory is believed to have a huge number of vacua – the so-called string theory landscape.
Outer space
Outer space has very low density and pressure, and is the closest physical approximation of a perfect vacuum. But no vacuum is truly perfect, not even in interstellar space, where there are still a few hydrogen atoms per cubic meter.[5]
Stars, planets, and moons keep their atmospheres by gravitational attraction, and as such, atmospheres have no clearly delineated boundary: the density of atmospheric gas simply decreases with distance from the object. The Earth's atmospheric pressure drops to about 3.2×10−2 Pa at 100 kilometres (62 mi) of altitude,[39] the Kármán line, which is a common definition of the boundary with outer space. Beyond this line, isotropic gas pressure rapidly becomes insignificant when compared to radiation pressure from the Sun and the dynamic pressure of the solar winds, so the definition of pressure becomes difficult to interpret. The thermosphere in this range has large gradients of pressure, temperature and composition, and varies greatly due to space weather. Astrophysicists prefer to use number density to describe these environments, in units of particles per cubic centimetre.
But although it meets the definition of outer space, the atmospheric density within the first few hundred kilometers above the Kármán line is still sufficient to produce significant drag on satellites. Most artificial satellites operate in this region called low Earth orbit and must fire their engines every few days to maintain orbit.[citation needed] The drag here is low enough that it could theoretically be overcome by radiation pressure on solar sails, a proposed propulsion system for interplanetary travel.[citation needed] Planets are too massive for their trajectories to be significantly affected by these forces, although their atmospheres are eroded by the solar winds.
All of the observable universe is filled with large numbers of photons, the so-called cosmic background radiation, and quite likely a correspondingly large number of neutrinos. The current temperature of this radiation is about 3 K, or −270 degrees Celsius or −454 degrees Fahrenheit.
Measurement
The quality of a vacuum is indicated by the amount of matter remaining in the system, so that a high quality vacuum is one with very little matter left in it. Vacuum is primarily measured by its absolute pressure, but a complete characterization requires further parameters, such as temperature and chemical composition. One of the most important parameters is the mean free path (MFP) of residual gases, which indicates the average distance that molecules will travel between collisions with each other. As the gas density decreases, the MFP increases, and when the MFP is longer than the chamber, pump, spacecraft, or other objects present, the continuum assumptions of fluid mechanics do not apply. This vacuum state is called high vacuum, and the study of fluid flows in this regime is called particle gas dynamics. The MFP of air at atmospheric pressure is very short, 70 nm, but at 100 mPa (~1×10−3 Torr) the MFP of room temperature air is roughly 100 mm, which is on the order of everyday objects such as vacuum tubes. The Crookes radiometer turns when the MFP is larger than the size of the vanes.
Vacuum quality is subdivided into ranges according to the technology required to achieve it or measure it. These ranges do not have universally agreed definitions, but a typical distribution is shown in the following table.[40][41] As we travel into orbit, outer space and ultimately intergalactic space, the pressure varies by several orders of magnitude.
| Vacuum quality | Torr | Pa | Atmosphere |
|---|---|---|---|
| Atmospheric pressure | 760 | 1.013×105 | 1 |
| Low vacuum | 760 to 25 | 1×105 to 3×103 | 9.87×10−1 to 3×10−2 |
| Medium vacuum | 25 to 1×10−3 | 3×103 to 1×10−1 | 3×10−2 to 9.87×10−7 |
| High vacuum | 1×10−3 to 1×10−9 | 1×10−1 to 1×10−7 | 9.87×10−7 to 9.87×10−13 |
| Ultra high vacuum | 1×10−9 to 1×10−12 | 1×10−7 to 1×10−10 | 9.87×10−13 to 9.87×10−16 |
| Extremely high vacuum | < 1×10−12 | < 1×10−10 | < 9.87×10−16 |
| Outer space | 1×10−6 to < 1×10−17 | 1×10−4 to < 3×10−15 | 9.87×10−10 to < 2.96×10−20 |
| Perfect vacuum | 0 | 0 | 0 |
- Atmospheric pressure is variable but standardized at 101.325 kPa (760 Torr).
- Low vacuum, also called rough vacuum or coarse vacuum, is vacuum that can be achieved or measured with rudimentary equipment such as a vacuum cleaner and a liquid column manometer.
- Medium vacuum is vacuum that can be achieved with a single pump, but the pressure is too low to measure with a liquid or mechanical manometer. It can be measured with a McLeod gauge, thermal gauge or a capacitive gauge.
- High vacuum is vacuum where the MFP of residual gases is longer than the size of the chamber or of the object under test. High vacuum usually requires multi-stage pumping and ion gauge measurement. Some texts differentiate between high vacuum and very high vacuum.
- Ultra high vacuum requires baking the chamber to remove trace gases, and other special procedures. British and German standards define ultra high vacuum as pressures below 10−6 Pa (10−8 Torr).[42][43]
- Deep space is generally much more empty than any artificial vacuum. It may or may not meet the definition of high vacuum above, depending on what region of space and astronomical bodies are being considered. For example, the MFP of interplanetary space is smaller than the size of the Solar System, but larger than small planets and moons. As a result, solar winds exhibit continuum flow on the scale of the Solar System, but must be considered a bombardment of particles with respect to the Earth and Moon.
- Perfect vacuum is an ideal state of no particles at all. It cannot be achieved in a laboratory, although there may be small volumes which, for a brief moment, happen to have no particles of matter in them. Even if all particles of matter were removed, there would still be photons and gravitons, as well as dark energy, virtual particles, and other aspects of the quantum vacuum.
- Hard vacuum and soft vacuum are terms that are defined with a dividing line defined differently by different sources, such as 1 Torr,[44][45] or 0.1 Torr,[46] the common denominator being that a hard vacuum is a higher vacuum than a soft one.
Relative versus absolute measurement
Vacuum is measured in units of pressure, typically as a subtraction relative to ambient atmospheric pressure on Earth. But the amount of relative measurable vacuum varies with local conditions. On the surface of Jupiter, where ground level atmospheric pressure is much higher than on Earth, much higher relative vacuum readings would be possible. On the surface of the moon with almost no atmosphere, it would be extremely difficult to create a measurable vacuum relative to the local environment.
Similarly, much higher than normal relative vacuum readings are possible deep in the Earth's ocean. A submarine maintaining an internal pressure of 1 atmosphere submerged to a depth of 10 atmospheres (98 metres; a 9.8 metre column of seawater has the equivalent weight of 1 atm) is effectively a vacuum chamber keeping out the crushing exterior water pressures, though the 1 atm inside the submarine would not normally be considered a vacuum.
Therefore, to properly understand the following discussions of vacuum measurement, it is important that the reader assumes the relative measurements are being done on Earth at sea level, at exactly 1 atmosphere of ambient atmospheric pressure.
Measurements relative to 1 atm
The SI unit of pressure is the pascal (symbol Pa), but vacuum is often measured in torrs, named for Torricelli, an early Italian physicist (1608–1647). A torr is equal to the displacement of a millimeter of mercury (mmHg) in a manometer with 1 torr equaling 133.3223684 pascals above absolute zero pressure. Vacuum is often also measured on the barometric scale or as a percentage of atmospheric pressure in bars or atmospheres. Low vacuum is often measured in millimeters of mercury (mmHg) or pascals (Pa) below standard atmospheric pressure. "Below atmospheric" means that the absolute pressure is equal to the current atmospheric pressure.
In other words, most low vacuum gauges that read, for example 50.79 Torr. Many inexpensive low vacuum gauges have a margin of error and may report a vacuum of 0 Torr but in practice this generally requires a two-stage rotary vane or other medium type of vacuum pump to go much beyond (lower than) 1 torr.
Measuring instruments
Many devices are used to measure the pressure in a vacuum, depending on what range of vacuum is needed.[47]
Hydrostatic gauges (such as the mercury column manometer) consist of a vertical column of liquid in a tube whose ends are exposed to different pressures. The column will rise or fall until its weight is in equilibrium with the pressure differential between the two ends of the tube. The simplest design is a closed-end U-shaped tube, one side of which is connected to the region of interest. Any fluid can be used, but mercury is preferred for its high density and low vapour pressure. Simple hydrostatic gauges can measure pressures ranging from 1 torr (100 Pa) to above atmospheric. An important variation is the McLeod gauge which isolates a known volume of vacuum and compresses it to multiply the height variation of the liquid column. The McLeod gauge can measure vacuums as high as 10−6 torr (0.1 mPa), which is the lowest direct measurement of pressure that is possible with current technology. Other vacuum gauges can measure lower pressures, but only indirectly by measurement of other pressure-controlled properties. These indirect measurements must be calibrated via a direct measurement, most commonly a McLeod gauge.[48]
The kenotometer is a particular type of hydrostatic gauge, typically used in power plants using steam turbines. The kenotometer measures the vacuum in the steam space of the condenser, that is, the exhaust of the last stage of the turbine.[49]
Mechanical or elastic gauges depend on a Bourdon tube, diaphragm, or capsule, usually made of metal, which will change shape in response to the pressure of the region in question. A variation on this idea is the capacitance manometer, in which the diaphragm makes up a part of a capacitor. A change in pressure leads to the flexure of the diaphragm, which results in a change in capacitance. These gauges are effective from 103 torr to 10−4 torr, and beyond.
Thermal conductivity gauges rely on the fact that the ability of a gas to conduct heat decreases with pressure. In this type of gauge, a wire filament is heated by running current through it. A thermocouple or Resistance Temperature Detector (RTD) can then be used to measure the temperature of the filament. This temperature is dependent on the rate at which the filament loses heat to the surrounding gas, and therefore on the thermal conductivity. A common variant is the Pirani gauge which uses a single platinum filament as both the heated element and RTD. These gauges are accurate from 10 torr to 10−3 torr, but they are sensitive to the chemical composition of the gases being measured.
Ionization gauges are used in ultrahigh vacuum. They come in two types: hot cathode and cold cathode. In the hot cathode version an electrically heated filament produces an electron beam. The electrons travel through the gauge and ionize gas molecules around them. The resulting ions are collected at a negative electrode. The current depends on the number of ions, which depends on the pressure in the gauge. Hot cathode gauges are accurate from 10−3 torr to 10−10 torr. The principle behind cold cathode version is the same, except that electrons are produced in a discharge created by a high voltage electrical discharge. Cold cathode gauges are accurate from 10−2 torr to 10−9 torr. Ionization gauge calibration is very sensitive to construction geometry, chemical composition of gases being measured, corrosion and surface deposits. Their calibration can be invalidated by activation at atmospheric pressure or low vacuum. The composition of gases at high vacuums will usually be unpredictable, so a mass spectrometer must be used in conjunction with the ionization gauge for accurate measurement.[50]
Uses
Vacuum is useful in a variety of processes and devices. Its first widespread use was in the incandescent light bulb to protect the filament from chemical degradation. The chemical inertness produced by a vacuum is also useful for electron beam welding, cold welding, vacuum packing and vacuum frying. Ultra-high vacuum is used in the study of atomically clean substrates, as only a very good vacuum preserves atomic-scale clean surfaces for a reasonably long time (on the order of minutes to days). High to ultra-high vacuum removes the obstruction of air, allowing particle beams to deposit or remove materials without contamination. This is the principle behind chemical vapor deposition, physical vapor deposition, and dry etching which are essential to the fabrication of semiconductors and optical coatings, and to surface science. The reduction of convection provides the thermal insulation of thermos bottles. Deep vacuum lowers the boiling point of liquids and promotes low temperature outgassing which is used in freeze drying, adhesive preparation, distillation, metallurgy, and process purging. The electrical properties of vacuum make electron microscopes and vacuum tubes possible, including cathode ray tubes. Vacuum interrupters are used in electrical switchgear. Vacuum arc processes are industrially important for production of certain grades of steel or high purity materials. The elimination of air friction is useful for flywheel energy storage and ultracentrifuges.
Vacuum-driven machines[edit]
Vacuums are commonly used to produce suction, which has an even wider variety of applications. The Newcomen steam engine used vacuum instead of pressure to drive a piston. In the 19th century, vacuum was used for traction on Isambard Kingdom Brunel's experimental atmospheric railway. Vacuum brakes were once widely used on trains in the UK but, except on heritage railways, they have been replaced by air brakes.
Manifold vacuum can be used to drive accessories on automobiles. The best-known application is the vacuum servo, used to provide power assistance for the brakes. Obsolete applications include vacuum-driven windscreen wipers and Autovac fuel pumps. Some aircraft instruments (Attitude Indicator (AI) and the Heading Indicator (HI)) are typically vacuum-powered, as protection against loss of all (electrically powered) instruments, since early aircraft often did not have electrical systems, and since there are two readily available sources of vacuum on a moving aircraft, the engine and an external venturi. Vacuum induction melting uses electromagnetic induction within a vacuum.
Maintaining a vacuum in the Condenser is an important aspect of the efficient operation of steam turbines. A steam jet ejector or liquid ring vacuum pump is used for this purpose. The typical vacuum maintained in the Condenser steam space at the exhaust of the turbine (also called Condenser Backpressure) is in the range 5 to 15 kPa (absolute), depending on the type of condenser and the ambient conditions.
Outgassing
Evaporation and sublimation into a vacuum is called outgassing. All materials, solid or liquid, have a small vapour pressure, and their outgassing becomes important when the vacuum pressure falls below this vapour pressure. Outgassing has the same effect as a leak and can limit the achievable vacuum. Outgassing products may condense on nearby colder surfaces, which can be troublesome if they obscure optical instruments or react with other materials. This is of great concern to space missions, where an obscured telescope or solar cell can ruin an expensive mission.
The most prevalent outgassing product in vacuum systems is water absorbed by chamber materials. It can be reduced by desiccating or baking the chamber, and removing absorbent materials. Outgassed water can condense in the oil of rotary vane pumps and reduce their net speed drastically if gas ballasting is not used. High vacuum systems must be clean and free of organic matter to minimize outgassing.
Ultra-high vacuum systems are usually baked, preferably under vacuum, to temporarily raise the vapour pressure of all outgassing materials and boil them off. Once the bulk of the outgassing materials are boiled off and evacuated, the system may be cooled to lower vapour pressures and minimize residual outgassing during actual operation. Some systems are cooled well below room temperature by liquid nitrogen to shut down residual outgassing and simultaneously cryopump the system.
Pumping and ambient air pressure
Fluids cannot generally be pulled, so a vacuum cannot be created by suction. Suction can spread and dilute a vacuum by letting a higher pressure push fluids into it, but the vacuum has to be created first before suction can occur. The easiest way to create an artificial vacuum is to expand the volume of a container. For example, the diaphragm muscle expands the chest cavity, which causes the volume of the lungs to increase. This expansion reduces the pressure and creates a partial vacuum, which is soon filled by air pushed in by atmospheric pressure.
To continue evacuating a chamber indefinitely without requiring infinite growth, a compartment of the vacuum can be repeatedly closed off, exhausted, and expanded again. This is the principle behind positive displacement pumps, like the manual water pump for example. Inside the pump, a mechanism expands a small sealed cavity to create a vacuum. Because of the pressure differential, some fluid from the chamber (or the well, in our example) is pushed into the pump's small cavity. The pump's cavity is then sealed from the chamber, opened to the atmosphere, and squeezed back to a minute size.
The above explanation is merely a simple introduction to vacuum pumping, and is not representative of the entire range of pumps in use. Many variations of the positive displacement pump have been developed, and many other pump designs rely on fundamentally different principles. Momentum transfer pumps, which bear some similarities to dynamic pumps used at higher pressures, can achieve much higher quality vacuums than positive displacement pumps. Entrapment pumps can capture gases in a solid or absorbed state, often with no moving parts, no seals and no vibration. None of these pumps are universal; each type has important performance limitations. They all share a difficulty in pumping low molecular weight gases, especially hydrogen, helium, and neon.
The lowest pressure that can be attained in a system is also dependent on many things other than the nature of the pumps. Multiple pumps may be connected in series, called stages, to achieve higher vacuums. The choice of seals, chamber geometry, materials, and pump-down procedures will all have an impact. Collectively, these are called vacuum technique. And sometimes, the final pressure is not the only relevant characteristic. Pumping systems differ in oil contamination, vibration, preferential pumping of certain gases, pump-down speeds, intermittent duty cycle, reliability, or tolerance to high leakage rates.
In ultra high vacuum systems, some very "odd" leakage paths and outgassing sources must be considered. The water absorption of aluminium and palladium becomes an unacceptable source of outgassing, and even the adsorptivity of hard metals such as stainless steel or titanium must be considered. Some oils and greases will boil off in extreme vacuums. The permeability of the metallic chamber walls may have to be considered, and the grain direction of the metallic flanges should be parallel to the flange face.
The lowest pressures currently achievable in laboratory are about 10−13 torr (13 pPa).[51] However, pressures as low as 5×10−17 Torr (6.7 fPa) have been indirectly measured in a 4 K cryogenic vacuum system.[4] This corresponds to ≈100 particles/cm3.
Effects on humans and animals
Humans and animals exposed to vacuum will lose consciousness after a few seconds and die of hypoxia within minutes, but the symptoms are not nearly as graphic as commonly depicted in media and popular culture. The reduction in pressure lowers the temperature at which blood and other body fluids boil, but the elastic pressure of blood vessels ensures that this boiling point remains above the internal body temperature of 37 °C.[52] Although the blood will not boil, the formation of gas bubbles in bodily fluids at reduced pressures, known as ebullism, is still a concern. The gas may bloat the body to twice its normal size and slow circulation, but tissues are elastic and porous enough to prevent rupture.[53] Swelling and ebullism can be restrained by containment in a flight suit. Shuttle astronauts wore a fitted elastic garment called the Crew Altitude Protection Suit (CAPS) which prevents ebullism at pressures as low as 2 kPa (15 Torr).[54] Rapid boiling will cool the skin and create frost, particularly in the mouth, but this is not a significant hazard.
Animal experiments show that rapid and complete recovery is normal for exposures shorter than 90 seconds, while longer full-body exposures are fatal and resuscitation has never been successful.[55] A study by NASA on eight chimpanzees found all of them survived two and a half minute exposures to vacuum.[56] There is only a limited amount of data available from human accidents, but it is consistent with animal data. Limbs may be exposed for much longer if breathing is not impaired.[57] Robert Boyle was the first to show in 1660 that vacuum is lethal to small animals.
An experiment indicates that plants are able to survive in a low pressure environment (1.5 kPa) for about 30 minutes.[58][59]
During 1942, in one of a series of experiments on human subjects for the Luftwaffe, the Nazi regime experimented on prisoners in Dachau concentration camp by exposing them to low pressure.[60]
Cold or oxygen-rich atmospheres can sustain life at pressures much lower than atmospheric, as long as the density of oxygen is similar to that of standard sea-level atmosphere. The colder air temperatures found at altitudes of up to 3 km generally compensate for the lower pressures there.[57] Above this altitude, oxygen enrichment is necessary to prevent altitude sickness in humans that did not undergo prior acclimatization, and spacesuits are necessary to prevent ebullism above 19 km.[57] Most spacesuits use only 20 kPa (150 Torr) of pure oxygen. This pressure is high enough to prevent ebullism, but decompression sickness and gas embolisms can still occur if decompression rates are not managed.
Rapid decompression can be much more dangerous than vacuum exposure itself. Even if the victim does not hold his or her breath, venting through the windpipe may be too slow to prevent the fatal rupture of the delicate alveoli of the lungs.[57] Eardrums and sinuses may be ruptured by rapid decompression, soft tissues may bruise and seep blood, and the stress of shock will accelerate oxygen consumption leading to hypoxia.[61] Injuries caused by rapid decompression are called barotrauma. A pressure drop of 13 kPa (100 Torr), which produces no symptoms if it is gradual, may be fatal if it occurs suddenly.[57]
Some extremophile microorganisms, such as tardigrades, can survive vacuum conditions for periods of days or weeks.[62]
Examples
| Pressure (Pa or kPa) | Pressure (Torr) | Mean Free Path | Molecules per cm3 | |
|---|---|---|---|---|
| Standard atmosphere, for comparison | 101.325 kPa | 760 | 66 nm | 2.5×1019[63] |
| Intense hurricane | approx. 87 to 95 kPa | 650 to 710 | ||
| Vacuum cleaner | approximately 80 kPa | 600 | 70 nm | 1019 |
| Steam turbine exhaust (Condenser Backpressure) | 9 kPa | |||
| liquid ring vacuum pump | approximately 3.2 kPa | 24 | 1.75 μm | 1018 |
| Mars atmosphere | 1.155 kPa to 0.03 kPa (mean 0.6 kPa) | 8.66 to 0.23 | ||
| freeze drying | 100 to 10 | 1 to 0.1 | 100 μm to 1 mm | 1016 to 1015 |
| Incandescent light bulb | 10 to 1 | 0.1 to 0.01 | 1 mm to 1 cm | 1015 to 1014 |
| Thermos bottle | 1 to 0.01 [1] | 10−2 to 10−4 | 1 cm to 1 m | 1014 to 1012 |
| Earth thermosphere | 1 Pa to 1×10−7 | 10−2 to 10−9 | 1 cm to 100 km | 1014 to 107 |
| Vacuum tube | 1×10−5 to 1×10−8 | 10−7 to 10−10 | 1 to 1,000 km | 109 to 106 |
| Cryopumped MBE chamber | 1×10−7 to 1×10−9 | 10−9 to 10−11 | 100 to 10,000 km | 107 to 105 |
| Pressure on the Moon | approximately 1×10−9 | 10−11 | 10,000 km | 4×105[64] |
| Interplanetary space | 11[1] | |||
| Interstellar space | 1[65] | |||
| Intergalactic space | 10−6[1] |
XXX . XXX zero null 0 1 2 3
Electron–molecule collision calculations using the -matrix method
The -matrix method is an embedding procedure which is based on the division of space into an inner region where the physics is complicated and an outer region for which greatly simplified equations can be solved. The method developed out of nuclear physics, where the effects of the inner region were simply parametrized, into atomic and molecular physics, where the full problem can be formulated and hopefully solved ab initio. In atomic physics -matrix based procedures are the method of choice for the ab initio calculation of electron collision parameters. There has been a number of -matrix procedures developed to treat the low-energy electron–molecule collision problem or particular aspects of this problem. These methods have been extended to both positron physics and the -matrix treatment of vibrational motion.
The physical basis of the -matrix method as well as its theoretical formulation are presented. Various electron scattering models within an -matrix formulation including static exchange, static exchange plus polarization and close coupling are described with reference to various computational implementations of the method; these are compared to similar models used within other scattering methods. The need for a balanced treatment of the target and continuum wave functions is emphasised. Extensions of close-coupling based models into the intermediate energy regime using pseudo-states is discussed, as is the adaptation of -matrix methods to problems involving photons.
The numerical realisation of the -matrix method is based on the adaptation of quantum chemistry codes in the inner region and asymptotic electron–atom scattering programs in the outer region. Use of bound state codes in scattering calculations raises issues involving continuum basis sets, appropriate orbitals, integral evaluation, orthogonalization, Hamiltonian construction and diagonalization which need to be addressed. The algorithms developed to resolve these issues are described as are ones associated with the outer region where methods to characterize resonances have received particular attention.
Results from a few illustrative calculations are discussed: (i) electron collisions with polar systems with water as an example; (ii) electron collisions with molecular ions focusing on H3+; (iii) electron collisions with organic species such as methane and uracil and (iv) positron–molecule collisions. Finally some outstanding issues that need to be addressed are mentioned.
The effect of superelastic electron - molecule collisions on the vibrational energy distribution function
Energy transfer between highly vibrationally excited CO molecules and low-energy electrons is studied using kinetic modeling. The results are compared with those of experimental measurements in optically pumped CO. The effect of vibrational energy transfer by electrons from the high towards the low vibrational levels of CO, previously observed in the experiments, is reproduced in calculations. The best agreement with the experiment is obtained for an electron concentration in the plasma of  , which is consistent with the previous measurements of the vibrationally stimulated ionization rate. The results of kinetic modelling calculations provide better insight into the kinetics of energy exchange between vibrationally excited molecules and electrons .
, which is consistent with the previous measurements of the vibrationally stimulated ionization rate. The results of kinetic modelling calculations provide better insight into the kinetics of energy exchange between vibrationally excited molecules and electrons .
 , which is consistent with the previous measurements of the vibrationally stimulated ionization rate. The results of kinetic modelling calculations provide better insight into the kinetics of energy exchange between vibrationally excited molecules and electrons .
, which is consistent with the previous measurements of the vibrationally stimulated ionization rate. The results of kinetic modelling calculations provide better insight into the kinetics of energy exchange between vibrationally excited molecules and electrons . Molecular Physics of Elementary Processes Relevant to Hypersonics: Electron-Molecule Collisions
Non-resonant, electron-impact, vibro-electronic excitation cross sections, involving vibrationally excited N2 molecules, to the mixed valence-Rydberg b,c,o 1Πu and b′,c′,e′ 1åu+ singlet states are presented. These cross sections are calculated using the so-called similarity approach, accounting for the vibronic coupling among excited states, and compared with the experiments and different theoretical calculations.
New cross sections for the electron-impact resonant vibrational excitation of CO2 molecule are calculated, for the symmetric stretching mode, as a function of the incident electron energy and for the transitions (υ i , 0,0)→(νf , 0,0) with νi = 0,1,2 and for some selected value of νf in the interval νi ≤νf ≤10. A resonance potential curve and associated widths are calculated using the R-matrix method. Rate coefficients, calculated by assuming a Maxwellian electron energy distribution function, are also presented for the same (νi , 0,0)→(νf , 0,0) transitions.
Electron-impact cross sections and rate coefficients for resonant vibrational excitations involving the diatomic species N2, NO, CO, O2and H2, for multi-quantic and mono-quantic transitions, are reviewed along with the cross sections and rates for the process of the dissociative electron attachment to H2 molecule, involving a Rydberg excited resonant state of the H2- ion.
Electron collisions with atoms, ions, molecules, and surfaces: Fundamental science empowering advances in technology
Electron collisions with atoms, ions, molecules, and surfaces are critically important to the understanding and modeling of low-temperature plasmas (LTPs), and so in the development of technologies based on LTPs. Recent progress in obtaining experimental benchmark data and the development of highly sophisticated computational methods is highlighted. With the cesium-based diode-pumped alkali laser and remote plasma etching of Si3N4 as examples, we demonstrate how accurate and comprehensive datasets for electron collisions enable complex modeling of plasma-using technologies that empower our high-technology–based society.
Electron collisions with atoms, ions, molecules, and surfaces are critically important to the understanding and the modeling of laboratory plasmas, astrophysical processes, lasers, and planetary atmospheres, to name just a few examples. In addition to the investigation of naturally occurring phenomena, electron collisions form the basis of a vast array of plasma-using technologies, which continue to empower our high-technology–based society (1). Atomic, molecular, and optical (AMO) physics, the field that encompasses electron–atom and electron–molecule collisions, has made tremendous contributions to our fundamental understanding of nature. Despite the field’s longevity, breakthrough developments in atomic collisions continue to be made at the fundamental level of both experiment and theory.
The Need for Atomic and Molecular Data
In low-temperature plasmas (LTPs), electron and ion collisions with otherwise unreactive gas and surfaces activate those atoms and molecules through forming excited states, ions, and radicals. Those activated species are then used in applications ranging from microelectronics fabrication (2) to human healthcare (3). The most basic, necessary, and first step in the development of those technologies is the electron or ion impact with the initially unreactive species to produce the activated species. As a result, fundamental AMO physics is closely and beneficially connected to technology development.
Examples of experimental progress in advancing the knowledge base for LTPs include, but are certainly not limited to, the “magnetic angle changer” (MAC) (4) and the so-called “reaction microscope” (RM) (5). The MAC makes it possible to carry out measurements of electron impact cross sections in angular regimes that were previously inaccessible because of geometric limitations due to the position of the electron gun. Furthermore, taking advantage of dramatic improvements in detector technology and fast electronics, the RM has enabled unparalleled detailed studies of electron–atom and electron–molecule collision processes over a wide range of parameters (energies, angles), and so provided an extensive database to test theory.
At the same time, theoretical and particularly computational advances have made the calculation of data for atomic/molecular structure as well as electron collision processes both reliable and cost-effective, and hence enabled their use in models for technology development. Although the basic equations that describe these quantum-mechanical many-body phenomena are believed to be known with a high degree of confidence, their necessarily approximate solution—with an accuracy that allows for reliable quantitative predictions—remains a formidable challenge. As a result of collaborative efforts between experimentalists and theorists worldwide to produce benchmark data for thoroughly testing the existing and further developing theoretical/computational methods, theory has advanced to a point that there is now confidence in many theoretical predictions of fundamental collision processes for which no experimental data are (and possibly never will become) available, even though these data are required in self-consistent modeling efforts.
These developments and the improvement in our understanding of fundamental atomic collisions have been critical for advances in modeling electron-driven processes in plasmas. These models allow for the study of basic plasma processes, but also enable analysis and optimization of current technologies using plasmas, as well as predicting the performance of as-yet-unbuilt systems for new applications. There is no doubt that the fidelity, depth, and impact of the modeling depends on the quality of fundamental electron and ion scattering data (FSD). Modeling, therefore, is empowered by the availability and robustness of FSD. As mentioned already, of particular importance is the fact that much of the FSD used today are taken from theoretical rather than experimental efforts, a situation dictated by the enormous amount of data needed for these complex models, as well as both the difficulties and the costs associated with experimental investigations. It is therefore crucial that the quality of the FSD be assessed in a reliable way.
This Perspective is organized as follows. Using the examples of the cesium-based diode-pumped alkali laser (DPAL) and remote plasma etching of Si3N4, Examples of Modeling Needs illustrates the kind and amount of data that are needed to thoroughly model such systems. One of the many ingredients for a sophisticated model are cross sections for electron collisions with atoms and molecules, as well as atomic and molecular structure, data for atom–atom and atom–molecule collisions, interactions with the boundaries, etc. In this Perspective, we will focus on electron collisions. We devote Selected Recent Advances in Electron Collisions with Atoms and Molecules to highlight some recent experimental progress as well as theoretical developments in this field. Because these are only selected examples from the very large field of charged-particle collisions in AMO physics, references will be given that contain more comprehensive and detailed information. Connecting Fundamental Data with Modeling Applications presents two examples where extensive sets of electron collision data, obtained with highly sophisticated and validated computational models, have enabled the thorough modeling of the systems of interest. We finish with a few conclusions and an outlook regarding the likely future of this field.
Examples of Modeling Needs
Cs-Based DPAL.
DPALs are a class of optically pumped lasers that leverage inexpensive semiconductor diode lasers (DLs) to pump alkali vapor. The generally poor optical quality and the wide bandwidth of a DL is converted into high optical quality, narrow bandwidth from the alkali laser. Laser ionization based on resonance (LIBOR) is an efficient means to produce plasmas in alkali vapor with low laser intensity. Electron heating by superelastic relaxation of laser-produced excited species then rapidly avalanches to nearly full ionization.
In DPALs, large densities of resonant excited states in alkali vapor are produced by laser pumping. With preexisting or laser-generated seed electrons, superelastic electron heating and associative ionization may result in plasma formation through a LIBOR-like process. The resulting plasma has the potential to reduce or quench laser oscillation through electron collision mixing. Hence, a critical question concerns the importance of plasma formation in a given DPAL system.
Our specific example concerns the computational investigation of a pulsed DPAL in He/Cs/C2 H6 and He/Cs/N2 mixtures with lasing occurring on the Cs (6p)2 (6s)2S1/2 transition with a wavelength of 894 nm. Fig. 1 gives an impression of the species contained in the model and the processes that are accounted for. Data for electron collisions with Cs atoms are by no means the only pieces needed for the puzzle, but they turn out to be a very important ingredient—in addition to data for electron collisions with helium atoms and ions, their dimers, as well as nitrogen atoms, ions, and molecules formed by Cs, He, and N. We also emphasize that cross sections for collisions with Cs atoms in their ground state are not sufficient, but rather data for collisions with atoms in excited states, including short-lived species, are needed. Such data are extremely difficult to obtain experimentally, and hence modelers have to rely on theoretical predictions.
Fig. 1.
Scheme for modeling a Cs-based DPAL. The solid lines denote electron collisions that induce transitions between the ground state and all excited states, and to the ion. The dotted lines are representative of electron impact collisions that produce transitions between all excited states. Additional reactions include collisions between atoms and molecules, and radiative transitions. Also shown (thick dashed-dotted lines) are the pump and lasing transitions.
Remote Plasma Etching of Si3N4.
To fabricate modern microprocessors, hundreds of manufacturing steps are required, many of them involving LTPs to etch (remove material), deposit (add material), clean, and passivate surfaces. As feature sizes in microelectronics shrink, the devices become more sensitive to damage from the plasmas being used to fabricate the device. As a result, the plasma is often sustained remotely from the wafer being etched and so protect the wafer from the most damaging reactive species. The less damaging reactive species are then flowed to the wafer for processing. This procedure is called remote plasma etching.
The gas mixtures that may be used for plasma etching, and for remote plasma etching in particular, contain complex molecular feedstocks. The choice of feedstock is based on how electron impact dissociation and ionization can produce the desired activated species. For example, in remove plasma etching of Si3N4, mixtures of NF3 and O2 may be used to create NFx, N, and FNOx (x = 1–3) species that ultimately etch the wafer. In modeling these systems to assist with technology development, a large number of individual species and reactions between those species must be accounted for. A subset of the species and reactions that must be considered in an LTP sustained only in an NF3/O2 mixture is shown in Fig. 2. For each of the electron-mediated processes, highlighted in red, FSD are required as a function of electron energy and scattering angle. Here, the reactive process is initiated by electron impact on NF3 producing NF2 and F, and with O2 producing O atoms, and then followed by electron impact with those dissociation products. The availability of FSD for complex molecules such as NFx and the fragments are rate-limiting steps in developing models for LTP processes.
Fig. 2.
Reaction mechanism in NF3/O2 mixtures. “M” denotes a third body.
Selected Recent Advances in Electron Collisions with Atoms and Molecules
We now describe a few advances that have pushed the production of reliable atomic collision data forward significantly during the past two decades. No attempt is being made to be comprehensive, and we will only summarize the basic ideas. Interested readers should consult the references given.
Two Experimental Advances.
The basic workhorse used in a large number of electron-scattering studies is the electron spectrometer. Free electrons are formed into a beam and energy selected by various combinations of electrostatic and magnetic fields. The use of electrostatic fields is most common, because they are more easily controlled and shielded than their magnetic counterparts. This is particularly important when it is essential to preserve the direction of low-energy electrons following the collision process.
Fig. 3 exhibits an example of such a spectrometer (6), which combines the characteristics of a conventional electrostatic device with an important innovation. It can be used for elastic scattering and electron impact excitation studies. The electron gun consists of a source of electrons produced by thermionic emission from a heated filament. The electrons are collimated and focused by an electrostatic lens system onto the input aperture of a double hemispherical energy selector. Those electrons within a narrow band of energies satisfying the criteria for transmission through the selector are then focused on the gas beam produced by a nozzle arrangement. Scattered electrons from the interaction region traveling in the direction of the scattered electron analyzer are similarly focused onto the input aperture of its double hemispherical analyzer, and the transmitted electrons are finally being focused into a single-channel electron multiplier detector.
One drawback of conventional electron spectrometers is that the angular range of the electron analyzer is limited by the physical presence of other components of the spectrometer. This limitation was overcome by Read and Channing (4) who applied a localized static magnetic field to the interaction region of a conventional spectrometer. The incident electron beam and the scattered electrons are, respectively, steered to and from the interaction region through angles set by the field (hence, the common name “magnetic angle changer” or “MAC”). This steering means that electrons normally scattered into inaccessible scattering angles are rotated into the accessible angular range of the electron analyzer while the magnetic field design is such that it leaves the angular distribution of the electrons undistorted. The spectrometer shown in Fig. 3 has a MAC fitted, thereby enabling the full angular range 0–180° to be accessed.
Another novel experimental development in electron–atom/molecule scattering (and also heavy-particle collisions) is the reaction microscope described by Ullrich et al. (5). In contrast to conventional electron spectrometers, it uses recoil-ion and electron momentum spectroscopy to measure the vector momenta of outgoing charged particles.
A recent version, developed by Ren et al. (7) to study single ionization processes is shown in Fig. 4. The RM operates on entirely different principles from conventional electron spectrometers. Briefly, a pulsed beam of electrons crosses a supersonic atom beam. The ejected electrons and the recoiling ions are extracted in opposite directions by a weak uniform electric field parallel to the incident electron beam direction. A uniform magnetic field is also applied in this direction to confine electrons emitted perpendicular to the electric field. After passing through field-free drift regions, the slow ejected electrons are detected in two time- and position-sensitive multihit detectors, allowing for the vector momenta of all particles to be calculated. Unlike most conventional coincidence electron spectrometers, which only enable measurements in a single plane at any one time, this technique allows for data to be collected over a large part of the entire 4π solid angle simultaneously.
Fig. 4.
The reaction microscope of Ren et al. (7). The projectile-electron beam is crossed with a supersonic gas beam. The projectile is created by a pulsed UV laser illuminating a photocathode. The outgoing electrons and ions are extracted by a homogeneous electric (E) field, created by a series of parallel electrodes, and detected by 2D position- and time-sensitive multihit detectors. A pair of Helmholtz coils generates a uniform magnetic (B) field, which forces the electrons into cyclotron trajectories and guides them onto the detector. The time of flight for each particle from the collision region to the respective detector is determined by the clock signals from the projectile pulse and the detectors.
Without going into detail, we emphasize the difficulty of obtaining absolute cross sections. Most of the time, some cross-normalization to “known” (or believed to be known) other data, such as cross sections for another target in a mixed-flow setup, data for angle-integrated state-to-state transitions after performing angle-differential measurements, total (summed over all accessible exit channels) cross sections, or even theoretical predictions, is required. Only in exceptional cases, absolute total ionization or recombination cross sections can be obtained directly (after carefully determining many experimental parameters) and fed into plasma models. An example is the crossed-beam apparatus developed by Müller and collaborators (8, 9).
Two Theoretical Advances.
Recent advances in computational power have enabled enormous progress in the treatment of atomic and molecular collisions. Even for electron collisions alone, the number of techniques is so extensive that we are not aware of a single recent comprehensive review on the subject. A broad overview with a summary of the basic ideas behind various methods used today for electron–atom collisions can be found in ref. 10. Even more general, atomic and molecular structure, electron–molecule, and heavy-particle collisions are addressed in ref. 11. In the latter work, particular emphasis is placed on estimating the uncertainty associated with theoretical predictions. Although not easy to quantify, this was recently recognized as a very important issue (12).
Here, we only mention two approaches, the so-called convergent close-coupling (CCC) (13) method and various R-matrix with pseudostates (RMPS) formulations based on the ideas presented in (14). The former is formulated in momentum space and the latter in coordinate space. These different formulations have a number of practical consequences, but both methods are based on the time-independent close-coupling approximation, in which the total wavefunction of the -electron collision system is expanded in terms of a set of fully antisymmetrized products built from the N-electron target states and functions that describe the projectile. As described below, CCC and RMPS are fundamentally equivalent and hence should lead to the same result if the same target states are included in the expansion. For complex targets, of course, the atomic or molecular structure itself can be a major challenge, and care must be taken to ensure that correlations as well as relativistic effects are accounted for to sufficient accuracy in order for the subsequent collision calculation to be meaningful.
The close-coupling expansion results in a set of coupled integro-differential equations, either for the transition matrix elements in the CCC momentum–space formulation or for the unknown projectile wavefunction in coordinate space. Interestingly, the CCC equations for the transition matrix simplify for high projectile energies, whereas coordinate-space close coupling has been the method of choice for low-energy collisions for many years. In this context, “high” refers to incident projectile energies of several times the ionization threshold, whereas “low” refers to energies at which at most a few inelastic excitation processes are energetically possible. It is also worth mentioning that the R-matrix approach, as pioneered by Burke and collaborators (see ref. 15 for a comprehensive overview), is basically a numerical method to solve the close-coupling equations very efficiently for a large number of projectile energies. Hence, the method is particularly suitable when resonances change the energy dependence of the results dramatically, something that often happens in the low-energy near-threshold regime.
As one might expect from the description so far, the so-called “intermediate energies,” from about the ionization threshold to several times that energy, are the most difficult to handle. For this energy regime, channel coupling to an infinite (although countable) number of high-lying Rydberg states as well as the infinite (uncountable) target continuum spectrum is known to affect the results even for transitions between low-lying discrete states. To address this issue, so-called “pseudostates” are introduced that approximate these effects by including a large number (often several hundred) of square-integrable states in the close-coupling expansion. These states are not physical, because their wavefunctions are forced to vanish beyond some distance away from the target. Even though the expansion is no longer exact, the use of the pseudostates provides a general, and systematically improvable, way of accounting for this coupling. In addition, it enables the ab-initio calculation of ionization cross sections as the sum of all excitation cross sections to pseudostates with energies above the ionization threshold.
Over the years, enormous efforts have been dedicated to the general formulation, the construction of practical algorithms, and the development of general computer programs, many (although not all) of which are accessible to the general public. Here, we only mention the R-matrix package of the Belfast group (16) and the B-spline R-matrix (BSR) program of Zatsarinny (17). For a review of the BSR approach and a number of its applications, we refer to ref. 18.
In addition to the time-independent CCC and RMPS approaches, we mention the time-dependent close-coupling (TDCC) (19) formulation, as well as “exterior complex scaling” (ECS) (20). Both methods have provided important cross-checks for CCC and RMPS predictions, in particular because they can either avoid or treat in an alternative way the unphysical boundary conditions that must be handled in CCC and RMPS due to the finite range of the pseudostates. Although TDCC has also been used in some production calculations (generally to describe ionization processes), the computational effort required, as well as the quality of the target structure that can be used at this time, have limited the application of both TDCC and ECS regarding the mass production of atomic and molecular collision data. We also note that the current suite of CCC codes is limited to quasi one- and two-electron targets, i.e., at most two active electrons outside of an inert core without orbital or spin angular momentum can be handled. Although the general R-matrix packages may, in principle, be applied to complex targets with multiple open shells, the number of possible configurations and channels leads to practical limitations as well.
It should also be mentioned that the computational treatment relies on both supercomputer hardware such as Stampede (21), on which many of the recent BSR with pseudostates calculations have been performed, and on efficient, fully parallelized linear-algebra packages. For R-matrix approaches in particular, the complete diagonalization (i.e., the determination of all eigenvalues and eigenvectors) of nonsparse matrices is required. Recent calculations involved matrices of rank up to 200,000.
As mentioned earlier, there are many other methods around by which cross sections for electron collisions may be obtained. Variants of the relatively simple distorted-wave Born approximation remain important, especially if results from more sophisticated methods are not available. An example is the interface website to the Atomic Collision Codes (22) of the Los Alamos National Laboratory. Also, results have been collected in many databases. Some information can be found in ref. 23.
Some Illustrative Results.
We now discuss a few examples to show the current state of comparison between experiment and theory. Due to the experimental convenience, many of the benchmark studies have been carried out with noble gases, and hence most of our examples are also for such targets, namely electron-impact excitation of Ar and Kr as well as ionization of He and Ar. In addition, we show selected results for Cs and N targets.
Fig. 5 exhibits the differential cross section as a function of energy for electron-impact excitation of the 5s[3/2]2 and the 5s′[1/2]1 states of krypton (24). Both states have the dominant configuration 4p55s. The former is metastable (total electronic angular momentum ) and couples mainly to the (4p5)2P3/2 ionic core, whereas the latter with couples to the (4p5)2P1/2 core and can optically decay to the (4p6)1S0ground state. To indicate that the valence orbital is strongly term dependent, one commonly uses the notations 5s and 5s′, respectively.
Fig. 5.
Differential cross section for electron-impact excitation of Kr at a scattering angle of 180°. The experimental data are compared with predictions from a full-relativistic BSR model (24).
The overall agreement between the measurements and predictions from a full-relativistic 69-state BSR model is very satisfactory, particularly for the optically forbidden transition to the metastable state. Note how well the complex resonance structure in the energy range from about 10.5 to 13 eV is reproduced by the BSR theory. The remaining discrepancies very close to threshold are most likely due to experimental issues, whereas theory apparently has some problems left for the 5s′[1/2]1 state. Nevertheless, the unprecedented agreement between experiment and theory achieved in this study resolved discrepancies between previous measurements and calculations of angle-integrated cross sections for this collision system, as well as other heavy noble-gas targets (18).
Fig. 6 exhibits the experimental and theoretical fully differential cross section (FDCS) for ionization of helium by 70.6-eV electron impact as 3D polar plots (25). The two outgoing electrons share the excess energy of 46 eV equally. One electron is detected at a fixed angle , whereas the detection angle of the second electron is varied. In this presentation, the FDCS for a particular direction is given as the distance from the origin of the plot to the point on the surface, which is intersected by the ionized electron’s emission direction. For the purpose of the present Perspective, we only note that the agreement between experiment and the CCC prediction is excellent. More details, including a discussion of the physical background, can be found in ref. 25.
Fig. 6.
Three-dimensional representation of the FDCS for ionization of He(1s2) (25). The experimental patterns on the Left are compared with CCC predictions on the Right, for a fixed detection angle of one electron. The incident projectile energy is 70.6 eV, and both outgoing electrons have an energy of 23.0 eV.
Moving on to a more complex target, Fig. 7 exhibits the FDCSs for ionization of Ar(3p6) by 66-eV electron impact. In this case, the excess energy is shared unequally between the two electrons in the final state, with the fast one being detected at and the emission direction of the slow one with energy eV being varied. Although not perfect, the agreement between experiment and BSR is sufficiently good to provide significant confidence in the BSR prediction for this—and many other—electron collision problems involving atomic targets.
Fig. 7.
Three-dimensional representation of the FDCS for ionization of Ar(3p6) (26). The experimental patterns on the Left are compared with BRS predictions on the Right, for a fixed detection angle . The incident projectile energy is 66 eV, and the slower of the two outgoing electrons has an energy of 3 eV.
The detailed comparisons mentioned above subsequently had a significant impact on production calculations for angle-integrated cross sections for electron collisions. Two more examples are shown below. The first one concerns electron impact ionization of the four states with dominant configuration 3p54s from the (3p6)1S0 ground state in argon. Fig. 8 shows results from a detailed study using the BSR approach (27). Looking at the top two rows, we see the enormous effect of accounting for coupling to both high-lying discrete states and the ionization continuum on the results for these transitions from the ground state to the first four excited states. The effect is particularly strong for the metastable 4s[3/2]2 and 4s′[1/2]0 states. Somewhat surprisingly, however, the coupling effect also prevails for the excited states with electronic angular momentum for incident energies at least up to 100 eV. This fact suggests that simple models, such as a distorted-wave approach, would not be appropriate until such comparatively high energies. Semiempirical fixes to such models, as suggested by Kim (31) with so-called “BEf-scaling,” may help. However, such methods are limited to particular situations, and success is by no means guaranteed due to the lack of a firm theoretical foundation.
Fig. 8.
Angle-integrated cross sections for electron-impact excitation of the 3p54s states in argon from the (3p6)1S0 ground state (27). Top two rows: The results from a variety of BSR models (see text) are compared with each other to provide an indication of the convergence pattern in the theoretical predictions. Bottom two rows: The results from the BSR-31 and BSR-500 models are compared with a number of experimental data [28⇓⇓–30 and (Mochizuki Y, Murai H, Kato H, Hoshino M, Tanaka H (2015) Electron impact excitation of the low-lying 4s[3/2]1 and 4s'[1/2]1 levels in Ar atom. Proceedings of the XXIX International Conference on Photonic, Electronic, and Atomic Collisions (ICPEAC), Toledo (Spain). Poster MO-115, and private communication.)].
The bottom two rows of Fig. 8 exhibit the results again, this time as a comparison between the predictions from a 31-state model (coupling only the lowest 31 discrete states of Ar) and a 500-state model (including 78 discrete and 422 continuum pseudostates) with experimental data from several groups. Without going into details, we note that energy dependence seen in many of the individual datasets is very scattered, much more than one would expect in reality. Consequently, the experimental data apparently have significant uncertainties, most likely due to a combination of statistical and systematic effects. Based on the careful analysis of trends in the theoretical predictions (11), one would advise modelers to use the very comprehensive BSR-500 dataset (state-to-state transitions between the lowest 31 states plus ionization cross sections are available) rather than any of the few experimental data currently available.
The need for using theoretical rather than experimental data becomes even more apparent for targets that only form atoms under special conditions. An example is shown in Fig. 9, which depicts electron-impact excitation cross sections for a number of transitions in atomic rather than molecular nitrogen. Once again, predictions from a number of BSR models, with up to 690 states included in the close-coupling expansion, are compared with the few experimental data currently available for this collision system. The very large error bars associated with these experimental data, and just the few energy points for which they exist, clearly limits their use in practical applications. In contrast, the best BSR dataset, once again carefully analyzed with respect to the convergence of the close-coupling expansion, is expected to be both sufficiently comprehensive and accurate for most modeling applications.
Fig. 9.
Cross sections, as function of collision energy, for electron-impact excitation of the most important transitions from the (2s22p3)4So ground state of atomic nitrogen. The final states are listed in the various panels. Unless listed explicitly as 2s, the inner-shell configuration is 1s22s2. BSR-696 and BSR-61 results from ref. 32 are compared with those from previous BSR-39 and BSR-21 calculations (33). Also shown are various sets of experimental data (34⇓–36).
Space does not allow us to present further examples, in particular for atomic ions. In general, with growing ionic charge, the Coulomb interaction within the target and also between the target and the projectile electron increasingly dominates electron correlation and channel coupling effects. Hence, perturbative methods are likely to be more successful for these cases than for neutral targets, provided only the background cross sections are needed rather than a detailed analysis of resonances. Many of these systems are of tremendous importance in the interpretation of astrophysical observations. Once again, the enormous amount of data needed has made theoretical predictions essential. Nevertheless, carefully selected and planned experimental studies remain important for benchmark comparisons with theory.
Connecting Fundamental Data with Modeling Applications
We now return to the two examples mentioned in The Need for Atomic and Molecular Data, namely the Cs-based DPAL and remote plasma etching of Si3N4. To model these systems, a significant number of data for electron collisions with either the Cs atom or NFx molecules were required.
Cs-Based DPAL.
Optical pumping of Cs vapor and possible plasma formation was discussed in detail in a recent paper (37). It is an excellent example of a mutually beneficial collaboration between data producers and data users. As just a small subset of electron collision data needed for the modeling, Fig. 10 exhibits the cross sections for electron collisions with Cs in its excited (6p)2P3/2 state. Obtaining these cross sections experimentally from beam setups, or possibly from collisions in laser traps, is extremely challenging (39), due to the difficulties of preparing the target. Hence, the cross sections were obtained from full-relativistic BSR calculations based on the work reported in ref. 38 and cross-checked against independently generated results from an earlier, also highly successful semirelativistic model (40). Although one can never be sure, of course, there is every reason to believe that the rate coefficients, which were calculated from the electron collision cross sections, are accurate to better than 10%.
Fig. 10.
Cross sections predicted by the B-spline R-matrix with pseudostates approach for electron collisions with Cs atoms in the (6p)2P3/2 excited state (38).
An example of modeling the DPAL with numerically generated FSD is shown in Fig. 11. These results were produced with a global kinetics, collisional-radiative model (41), in which conservation equations for the densities of the charged and neutral species, electron temperature, gas temperature, and laser optical fluxes are integrated in time while accounting for transport in the form of diffusion to surfaces and/or plug flow. Rate and transport coefficients for electron impact processes were obtained from solutions of Boltzmann’s equation for the electron energy distribution with FSD for cross sections as input. A high-power, 20 kW/cm2, 1-μs pump pulse excites a 600-torr mixture of He/N2/Cs = 85/15/5 × 10−6 gas mixture at 400 K. The Cs density is determined by the metal vapor pressure. Results are shown for the hundredth in a series of pump pulses. Over the series of pulses, a plasma density of 2 × 1013 cm−3 is formed. During the pump pulse, lasing occurs that saturates the Cs (6s)2S1/2 and (6p)2P1/2 states. The higher excited states of Cs (5d)2D3/2,5/2 are largely produced by electron impact excitation from the Cs (6p)2P1/2,3/2 states. Note that electron impact cross sections for these excitation processes are particularly large.
Fig. 11.
Densities of Cs species and electrons during high-power DPAL pumping of a He/N2/Cs gas mixture at 600 torr and 400 K (37).
The above work revealed that heating of electrons by superelastic relaxation of the diode laser-excited Cs 2P1/2,3/2 resonant states leads to significant plasma formation. This plasma ultimately reduces the laser power by depletion of the ground state through ionization and by electron-collision mixing of the laser levels (37).
Remote Plasma Etching of Si3N4.
As seen from Fig. 2, modeling this process requires, among many other data, cross sections for electron collisions with NF3, NF2, NF, various molecular ions, as well as data for heavy-particle collisions. Fig. 12 shows results for NF2, for which no experimental data were available. The predictions were generated by Tennyson and collaborators (42) using the UK molecular R-matrix codes (43). After the success achieved by the RMPS and CCC approaches for atoms and atomic ions, the very same ideas were implemented in the molecular codes. As a result, accurate and sufficiently comprehensive datasets can now be generated to serve the modeling community.
Fig. 12.
Some cross sections used for the processes depicted in Fig. 2. The data for electron collisions with NF2, including momentum transfer, vibrational excitation (v), and dissociation into combinations of various molecular ions were generated by Tennyson and collaborators (42) with the UK molecular R-matrix codes (43).
Using these FSD, results from a model for a remote plasma sustained in an Ar/NF3/O2 = 5/10/100 gas mixture at 400 mtorr are shown in Fig. 13 for a power deposition of 900 W. The densities of the charged particles and electron temperature are shown as the gas flows through the plasma zone and downstream toward the etching chamber. NF3 and O2 rapidly dissociate in the plasma zone, largely due to electron impact dissociative attachment and excitation. The plasma is highly electronegative with a ratio of negative ions to electrons of about 20. The electron density increases during the flow to a maximum of 1.1 × 1010cm−3. The formation of negative ions is due to dissociative attachment (e + + F− and e + O + O−). In the plasma zone, the electron temperature is 3.5–4.0 eV. This high value is necessary to offset the high rate of electron loss due to attachment. Downstream of the power deposition zone, the plasma rapidly transitions to an ion–ion plasma mainly composed of F− and NO+.
Fig. 13.
Charged particle densities during remote plasma etching using an Ar/NF3/O2 gas mixture at 400 mtorr. Significant electron impact dissociation of the feedstock gases produce ions composed primarily of the dissociation products and their products through subsequent reactions.
Conclusions and Outlook
In this Perspective, we highlighted a few of the advances that have been made in basic research in the AMO physics field of electron–atom and electron–molecule collisions, from the beginning of quantum mechanics nearly a century ago to the highly sophisticated theoretical, computational, and experimental methods used today. Experimental and theoretical/computational efforts in basic research were coordinated to provide benchmark data for thoroughly testing the reliability of various theoretical approaches. As a result of these collaborative efforts, theory has advanced to a point that there is now confidence in many theoretical predictions of fundamental collision processes for which no experimental data are (and possibly never will become) available. However, these data are required in self-consistent modeling efforts for plasmas, and they have been used successfully in many occasions. The production of fundamental electron-scattering data in this manner is accelerating the development of society benefiting technologies.
Despite the maturity of the field of charged-particle collisions, benchmark comparisons between experiment and theory, as well as between predictions from independent, highly sophisticated approaches such as CCC, RMPS, BSR, TDCC, ECS, etc., remain invaluable for continued progress. Fundamental scattering data, critically evaluated with respect to their likely uncertainties, are essential for the empowerment of plasma modeling and, consequently, to further advance our high-technology–based society. Last, but certainly not least, we emphasize the continued need for experimental benchmark data, especially for complex systems, where theory still needs to be checked carefully.

++++++++++++++++++++++++++++++++++++++++++++++++++++++
++++++++++++++++++++++++++++++++++++++++++++++++++++++
++++++++++++++++++++++++++++++++++++++++++++++++++++++
++++++++++++++++++++++++++++++++++++++++++++++++++++++
























