Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency, which emphasizes the contrast to spatial frequency and angular frequency. The period is the duration of time of one cycle in a repeating event, so the period is the reciprocal of the frequency. For example, if a newborn baby's heart beats at a frequency of 120 times a minute, its period—the time interval between beats—is half a second (that is, 60 seconds divided by 120 beats). Frequency is an important parameter used in science and engineering to specify the rate of oscillatory and vibratory phenomena, such as mechanical vibrations, audio (sound) signals, radio waves, and light.

These three dots are flashing, or cycling, periodically—from lowest frequency (0.5 hertz) to highest frequency (2.0 hertz), top to bottom. For each flashing dot: "f" is the frequency in hertz, (Hz)—or the number of events per second (i.e., cycles per second)—that the dot flashes; while "T" is the period, or time, in seconds (s) of each cycle, (i.e., the number of seconds per cycle). Note T and f are reciprocal values to each other.
For cyclical processes, such as rotation, oscillations, or waves, frequency is defined as a number of cycles per unit time. In physics and engineering disciplines, such as optics, acoustics, and radio, frequency is usually denoted by a Latin letter f or by the Greek letter or ν (nu) (see e.g. Planck's formula).
The relation between the frequency and the period of a repeating event or oscillation is given by
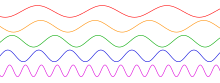
As time elapses—here moving left to right on the horizontal axis—the five sinusoidal waves vary, or cycle, regularly at different rates. The red wave (top) has the lowest frequency (i.e., cycles at the slowest rate) while the purple wave (bottom) has the highest frequency (cycles at the fastest rate).
The SI unit of frequency is the hertz (Hz), named after the German physicist Heinrich Hertz; one hertz means that an event repeats once per second. A previous name for this unit was cycles per second (cps). The SI unit for period is the second.
A traditional unit of measure used with rotating mechanical devices is revolutions per minute, abbreviated r/min or rpm. 60 rpm equals one hertz .
As a matter of convenience, longer and slower waves, such as ocean surface waves, tend to be described by wave period rather than frequency. Short and fast waves, like audio and radio, are usually described by their frequency instead of period. These commonly used conversions are listed below:
| Frequency | 1 mHz (10−3 Hz) | 1 Hz (100 Hz) | 1 kHz (103 Hz) | 1 MHz (106 Hz) | 1 GHz (109 Hz) | 1 THz (1012 Hz) |
|---|---|---|---|---|---|---|
| Period | 1 ks (103 s) | 1 s (100 s) | 1 ms (10−3 s) | 1 µs (10−6 s) | 1 ns (10−9 s) | 1 ps (10−12 s) |
- Angular frequency is commonly measured in radians per second (rad/s) but, for discrete-time signals, can also be expressed as radians per sample time, which is a dimensionless quantity. Angular frequency (in radians) is larger than regular frequency (in Hz) by a factor of 2π.
- Spatial frequency is analogous to temporal frequency, but the time axis is replaced by one or more spatial displacement axes. E.g.:
- Wavenumber, k, is the spatial frequency analogue of angular temporal frequency and is measured in radians per meter. In the case of more than one spatial dimension, wavenumber is a vector quantity.
In wave propagation
For periodic waves in nondispersive media (that is, media in which the wave speed is independent of frequency), frequency has an inverse relationship to the wavelength, λ (lambda). Even in dispersive media, the frequency f of a sinusoidal wave is equal to the phase velocity v of the wave divided by the wavelength λ of the wave:Measurement
Counting
Calculating the frequency of a repeating event is accomplished by counting the number of times that event occurs within a specific time period, then dividing the count by the length of the time period. For example, if 71 events occur within 15 seconds the frequency is:
A resonant-reed frequency meter, an obsolete device used from about 1900 to the 1940s for measuring the frequency of alternating current. It consists of a strip of metal with reeds of graduated lengths, vibrated by an electromagnet. When the unknown frequency is applied to the electromagnet, the reed which is resonant at that frequency will vibrate with large amplitude, visible next to the scale.
Stroboscope
An older method of measuring the frequency of rotating or vibrating objects is to use a stroboscope. This is an intense repetitively flashing light (strobe light) whose frequency can be adjusted with a calibrated timing circuit. The strobe light is pointed at the rotating object and the frequency adjusted up and down. When the frequency of the strobe equals the frequency of the rotating or vibrating object, the object completes one cycle of oscillation and returns to its original position between the flashes of light, so when illuminated by the strobe the object appears stationary. Then the frequency can be read from the calibrated readout on the stroboscope. A downside of this method is that an object rotating at an integral multiple of the strobing frequency will also appear stationary.Frequency counter
Higher frequencies are usually measured with a frequency counter. This is an electronic instrument which measures the frequency of an applied repetitive electronic signal and displays the result in hertz on a digital display. It uses digital logic to count the number of cycles during a time interval established by a precision quartz time base. Cyclic processes that are not electrical in nature, such as the rotation rate of a shaft, mechanical vibrations, or sound waves, can be converted to a repetitive electronic signal by transducers and the signal applied to a frequency counter. Frequency counters can currently cover the range up to about 100 GHz. This represents the limit of direct counting methods; frequencies above this must be measured by indirect methods.Heterodyne methods
Above the range of frequency counters, frequencies of electromagnetic signals are often measured indirectly by means of heterodyning (frequency conversion). A reference signal of a known frequency near the unknown frequency is mixed with the unknown frequency in a nonlinear mixing device such as a diode. This creates a heterodyne or "beat" signal at the difference between the two frequencies. If the two signals are close together in frequency the heterodyne is low enough to be measured by a frequency counter. This process only measures the difference between the unknown frequency and the reference frequency. To reach higher frequencies, several stages of heterodyning can be used. Current research is extending this method to infrared and light frequencies (optical heterodyne detection).Examples
Light
Visible light is an electromagnetic wave, consisting of oscillating electric and magnetic fields traveling through space. The frequency of the wave determines its color: 4×1014 Hz is red light, 8×1014 Hz is violet light, and between these (in the range 4-8×1014 Hz) are all the other colors of the visible spectrum. An electromagnetic wave can have a frequency less than 4×1014 Hz, but it will be invisible to the human eye; such waves are called infrared (IR) radiation. At even lower frequency, the wave is called a microwave, and at still lower frequencies it is called a radio wave. Likewise, an electromagnetic wave can have a frequency higher than 8×1014 Hz, but it will be invisible to the human eye; such waves are called ultraviolet (UV) radiation. Even higher-frequency waves are called X-rays, and higher still are gamma rays.
All of these waves, from the lowest-frequency radio waves to the highest-frequency gamma rays, are fundamentally the same, and they are all called electromagnetic radiation. They all travel through a vacuum at the same speed (the speed of light), giving them wavelengths inversely proportional to their frequencies.
where c is the speed of light (c in a vacuum, or less in other media), f is the frequency and λ is the wavelength.
In dispersive media, such as glass, the speed depends somewhat on frequency, so the wavelength is not quite inversely proportional to frequency.
Sound
Sound propagates as mechanical vibration waves of pressure and displacement, in air or other substances. Frequency is the property of sound that most determines pitch.
The frequencies an ear can hear are limited to a specific range of frequencies. The audible frequency range for humans is typically given as being between about 20 Hz and 20,000 Hz (20 kHz), though the high frequency limit usually reduces with age. Other species have different hearing ranges. For example, some dog breeds can perceive vibrations up to 60,000 Hz.
In many media, such as air, the speed of sound is approximately independent of frequency, so the wavelength of the sound waves (distance between repetitions) is approximately inversely proportional to frequency.
In music, a note is the pitch and duration of a sound, and also its representation in musical notation (♪, ♩). A note can also represent a pitch class. Notes are the building blocks of much written music: discretizations of musical phenomena that facilitate performance, comprehension, and analysis.[1]
The term note can be used in both generic and specific senses: one might say either "the piece 'Happy Birthday to You' begins with two notes having the same pitch", or "the piece begins with two repetitions of the same note". In the former case, one uses note to refer to a specific musical event; in the latter, one uses the term to refer to a class of events sharing the same pitch. (See also: Key signature names and translations.)
Two notes with fundamental frequencies in a ratio equal to any integer power of two (e.g., half, twice, or four times) are perceived as very similar. Because of that, all notes with these kinds of relations can be grouped under the same pitch class.
In traditional music theory, most countries in the world use the naming convention Do–Re–Mi–Fa–Sol–La–Si, including for instance Italy, Spain, France, Romania, most Latin American countries, Greece, Bulgaria, Turkey, Russia, and all the Arabic-speaking or Persian-speaking countries. However, within the English-speaking and Dutch-speaking world, pitch classes are typically represented by the first seven letters of the Latin alphabet (A, B, C, D, E, F and G). A few European countries, including Germany, adopt an almost identical notation, in which H substitutes for B (see below for details). In Indian music like Telugu Sa-Re-Ga-Ma-Pa-Da-Ni-Sa.(స రి గ మ ప ద ని స), Tamil (ச-ரி-க-ம-ப-த-நி) Byzantium used the names pa-vu-ga-di-ke-zo-ni-pa.
The eighth note, or octave, is given the same name as the first, but has double its frequency. The name octave is also used to indicate the span between a note and another with double frequency. To differentiate two notes that have the same pitch class but fall into different octaves, the system of scientific pitch notation combines a letter name with an Arabic numeral designating a specific octave. For example, the now-standard tuning pitch for most Western music, 440 Hz, is named a′ or A4.
There are two formal systems to define each note and octave, the Helmholtz pitch notation and the scientific pitch notation
Letter names are modified by the accidentals. A sharp ♯ raises a note by a semitone or half-step, and a flat ♭ lowers it by the same amount. In modern tuning a half step has a frequency ratio of 12√2, approximately 1.059. The accidentals are written after the note name: so, for example, F♯ represents F-sharp, B♭ is B-flat, and C♮ is C natural (or C).

Frequency vs Position on Treble Clef. Each note shown has a frequency of the previous note multiplied by 12√2
Additional accidentals are the double-sharp  , raising the frequency by two semitones, and double-flat
, raising the frequency by two semitones, and double-flat  , lowering it by that amount.
, lowering it by that amount.
In musical notation, accidentals are placed before the note symbols. Systematic alterations to the seven lettered pitches in the scale can be indicated by placing the symbols in the key signature, which then apply implicitly to all occurrences of corresponding notes. Explicitly noted accidentals can be used to override this effect for the remainder of a bar. A special accidental, the natural symbol ♮, is used to indicate an unmodified pitch. Effects of key signature and local accidentals do not accumulate. If the key signature indicates G♯, a local flat before a G makes it G♭ (not G♮), though often this type of rare accidental is expressed as a natural, followed by a flat (♮♭) to make this clear. Likewise (and more commonly), a double sharp  sign on a key signature with a single sharp ♯ indicates only a double sharp, not a triple sharp.
sign on a key signature with a single sharp ♯ indicates only a double sharp, not a triple sharp.
Assuming enharmonicity, many accidentals will create equivalences between pitches that are written differently. For instance, raising the note B to B♯ is equal to the note C. Assuming all such equivalences, the complete chromatic scale adds five additional pitch classes to the original seven lettered notes for a total of 12 (the 13th note completing the octave), each separated by a half-step.
Notes that belong to the diatonic scale relevant in the context are sometimes called diatonic notes; notes that do not meet that criterion are then sometimes called chromatic notes.
Another style of notation, rarely used in English, uses the suffix "is" to indicate a sharp and "es" (only "s" after A and E) for a flat, e.g., Fis for F♯, Ges for G♭, Es for E♭. This system first arose in Germany and is used in almost all European countries whose main language is not English, Greek, or a Romance language.
In most countries using these suffixes, the letter H is used to represent what is B natural in English, the letter B is used instead of B♭, and Heses (i.e., H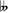 ) is used instead of B
) is used instead of B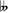 (although Bes and Heses both denote the English B
(although Bes and Heses both denote the English B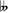 ). Dutch-speakers in Belgium and the Netherlands use the same suffixes, but applied throughout to the notes A to G, so that B, B♭ and B
). Dutch-speakers in Belgium and the Netherlands use the same suffixes, but applied throughout to the notes A to G, so that B, B♭ and B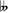 have the same meaning as in English, although they are called B, Bes, and Beses instead of B, B flat and B double flat. Denmark also uses H, but uses Bes instead of Heses for B
have the same meaning as in English, although they are called B, Bes, and Beses instead of B, B flat and B double flat. Denmark also uses H, but uses Bes instead of Heses for B .
.
The table below shows each octave and the frequencies for every note of pitch class A. The traditional (Helmholtz) system centers on the great octave (with capital letters) and small octave (with lower case letters). Lower octaves are named "contra" (with primes before), higher ones "lined" (with primes after). Another system (scientific) suffixes a number (starting with 0, or sometimes −1). In this system A4 is nowadays standardised at 440 Hz, lying in the octave containing notes from C4 (middle C) to B4. The lowest note on most pianos is A0, the highest C8. The MIDI system for electronic musical instruments and computers uses a straight count starting with note 0 for C−1 at 8.1758 Hz up to note 127 for G9 at 12,544 Hz.

Frequency vs Position on Treble Clef. Each note shown has a frequency of the previous note multiplied by 12√2
| Octave naming systems | frequency of A (Hz) | |||
|---|---|---|---|---|
| traditional | Helmholtz | scientific | MIDI | |
| subsubcontra | C͵͵͵ – B͵͵͵ | C−1 – B−1 | 0 – 11 | 13.75 |
| sub-contra | C͵͵ – B͵͵ | C0 – B0 | 12 – 23 | 27.5 |
| contra | C͵ – B͵ | C1 – B1 | 24 – 35 | 55 |
| great | C – B | C2 – B2 | 36 – 47 | 110 |
| small | c – b | C3 – B3 | 48 – 59 | 220 |
| one-lined | c′ – b′ | C4 – B4 | 60 – 71 | 440 |
| two-lined | c′′ – b′′ | C5 – B5 | 72 – 83 | 880 |
| three-lined | c′′′ – b′′′ | C6 – B6 | 84 – 95 | 1760 |
| four-lined | c′′′′ – b′′′′ | C7 – B7 | 96 – 107 | 3520 |
| five-lined | c′′′′′ – b′′′′′ | C8 – B8 | 108 – 119 | 7040 |
| six-lined | c′′′′′′ – b′′′′′′ | C9 – B9 | 120 – 127 C to G | 14080 |
Written notes[edit]
A written note can also have a note value, a code that determines the note's relative duration. In order of halving duration, they are: double note (breve); whole note (semibreve); half note (minim); quarter note (crotchet); eighth note (quaver); sixteenth note (semiquaver).; thirty-second note (demisemiquaver), sixty-fourth note (hemidemisemiquaver), and hundred twenty-eighth note.
In a score, each note is assigned a specific vertical position on a staff position (a line or space) on the staff, as determined by the clef. Each line or space is assigned a note name. These names are memorized by musicians and allow them to know at a glance the proper pitch to play on their instruments.

The staff above shows the notes C, D, E, F, G, A, B, C and then in reverse order, with no key signature or accidentals.

Note frequency (hertz)[edit]
In all technicality, music can be composed of notes at any arbitrary physical[clarification needed] frequency. Since the physical causes of music are vibrations of mechanical systems, they are often measured in hertz (Hz), with 1 Hz meaning one vibration per second. For historical and other reasons, especially in Western music, only twelve notes of fixed frequencies are used. These fixed frequencies are mathematically related to each other, and are defined around the central note, A4. The current "standard pitch" or modern "concert pitch" for this note is 440 Hz, although this varies in actual practice (see History of pitch standards).
The note-naming convention specifies a letter, any accidentals, and an octave number. Each note is an integer number of half-steps away from concert A (A4). Let this distance be denoted n. If the note is above A4, then n is positive; if it is below A4, then n is negative. The frequency of the note (f) (assuming equal temperament) is then:
For example, one can find the frequency of C5, the first C above A4. There are 3 half-steps between A4 and C5 (A4 → A♯4 → B4 → C5), and the note is above A4, so n = 3. The note's frequency is:
To find the frequency of a note below A4, the value of n is negative. For example, the F below A4 is F4. There are 4 half-steps (A4 → A♭4 → G4 → G♭4 → F4), and the note is below A4, so n = −4. The note's frequency is:
Finally, it can be seen from this formula that octaves automatically yield powers of two times the original frequency, since n is a multiple of 12 (12k, where k is the number of octaves up or down), and so the formula reduces to:
yielding a factor of 2. In fact, this is the means by which this formula is derived, combined with the notion of equally-spaced intervals.
The distance of an equally tempered semitone is divided into 100 cents. So 1200 cents are equal to one octave — a frequency ratio of 2:1. This means that a cent is precisely equal to 1200√2, which is approximately 1.000578.
For use with the MIDI (Musical Instrument Digital Interface) standard, a frequency mapping is defined by:
where p is the MIDI note number (and 69 is the number of semitones between C−1 (note 0) and A4). And in the opposite direction, to obtain the frequency from a MIDI note p, the formula is defined as:
For notes in an A440 equal temperament, this formula delivers the standard MIDI note number (p). Any other frequencies fill the space between the whole numbers evenly. This lets MIDI instruments be tuned accurately in any microtuning scale, including non-western traditional tunings.
Music and mathematics
Music theory has no axiomatic foundation in modern mathematics, yet the basis of musical sound can be described mathematically (in acoustics) and exhibits "a remarkable array of number properties".Elements of music such as its form, rhythm and metre, the pitches of its notes and the tempo of its pulse can be related to the measurement of time and frequency, offering ready analogies in geometry.
The attempt to structure and communicate new ways of composing and hearing music has led to musical applications of set theory, abstract algebra and number theory. Some composers have incorporated the golden ratio and Fibonacci numbers into their work .

A spectrogram of a violin waveform, with linear frequency on the vertical axis and time on the horizontal axis. The bright lines show how the spectral components change over time. The intensity coloring is logarithmic (black is −120 dBFS).
Time, rhythm and meter
Without the boundaries of rhythmic structure – a fundamental equal and regular arrangement of pulse repetition, accent, phrase and duration – music would not be possible.[10] Modern musical use of terms like meter and measure also reflects the historical importance of music, along with astronomy, in the development of counting, arithmetic and the exact measurement of time and periodicity that is fundamental to physics.The elements of musical form often build strict proportions or hypermetric structures (powers of the numbers 2 and 3).
Musical form
Musical form is the plan by which a short piece of music is extended. The term "plan" is also used in architecture, to which musical form is often compared. Like the architect, the composer must take into account the function for which the work is intended and the means available, practicing economy and making use of repetition and order.[12] The common types of form known as binary and ternary ("twofold" and "threefold") once again demonstrate the importance of small integral values to the intelligibility and appeal of music.Frequency and harmony

Chladni figures produced by sound vibrations in fine powder on a square plate. (Ernst Chladni, Acoustics, 1802)
Succeeding superoctaves are pitches found at frequencies four, eight, sixteen times, and so on, of the fundamental frequency. Pitches at frequencies of half, a quarter, an eighth and so on of the fundamental are called suboctaves. There is no case in musical harmony where, if a given pitch be considered accordant, that its octaves are considered otherwise. Therefore, any note and its octaves will generally be found similarly named in musical systems (e.g. all will be called doh or A or Sa, as the case may be).
When expressed as a frequency bandwidth an octave A2–A3 spans from 110 Hz to 220 Hz (span=110 Hz). The next octave will span from 220 Hz to 440 Hz (span=220 Hz). The third octave spans from 440 Hz to 880 Hz (span=440 Hz) and so on. Each successive octave spans twice the frequency range of the previous octave.
Because we are often interested in the relations or ratios between the pitches (known as intervals) rather than the precise pitches themselves in describing a scale, it is usual to refer to all the scale pitches in terms of their ratio from a particular pitch, which is given the value of one (often written 1/1), generally a note which functions as the tonic of the scale. For interval size comparison, cents are often used.
Common name Example
name
HzMultiple
of fundamentalRatio
within octaveCents
within octaveFundamental A2,
1101x1/1 = 1x 0Octave A3
2202x2/1 = 2x 12002/2 = 1x 0Perfect Fifth E4
3303x3/2 = 1.5x 702Octave A4
4404x4/2 = 2x 12004/4 = 1x 0Major Third C♯5
5505x5/4 = 1.25x 386Perfect Fifth E5
6606x6/4 = 1.5x 702Harmonic seventh G5
7707x7/4 = 1.75x 969Octave A5
8808x8/4 = 2x 12008/8 = 1x 0
Tuning systems
There are two main families of tuning systems: equal temperament and just tuning. Equal temperament scales are built by dividing an octave into intervals which are equal on a logarithmic scale, which results in perfectly evenly divided scales, but with ratios of frequencies which are irrational numbers. Just scales are built by multiplying frequencies by rational numbers, which results in simple ratios between frequencies, but with scale divisions that are uneven.One major difference between equal temperament tunings and just tunings is differences in acoustical beat when two notes are sounded together, which affects the subjective experience of consonance and dissonance. Both of these systems, and the vast majority of music in general, have scales that repeat on the interval of every octave, which is defined as frequency ratio of 2:1. In other words, every time the frequency is doubled, the given scale repeats.
Below are Ogg Vorbis files demonstrating the difference between just intonation and equal temperament. You may need to play the samples several times before you can pick the difference.
- Two sine waves played consecutively – this sample has half-step at 550 Hz (C♯ in the just intonation scale), followed by a half-step at 554.37 Hz (C♯ in the equal temperament scale).
- Same two notes, set against an A440 pedal – this sample consists of a "dyad". The lower note is a constant A (440 Hz in either scale), the upper note is a C♯ in the equal-tempered scale for the first 1", and a C♯ in the just intonation scale for the last 1". Phase differences make it easier to pick the transition than in the previous sample.
Just tunings
5-limit tuning, the most common form of just intonation, is a system of tuning using tones that are regular number harmonics of a single fundamental frequency. This was one of the scales Johannes Kepler presented in his Harmonices Mundi (1619) in connection with planetary motion. The same scale was given in transposed form by Scottish mathematician and musical theorist, Alexander Malcolm, in 1721 in his 'Treatise of Musick: Speculative, Practical and Historical',[13] and by theorist Jose Wuerschmidt in the 20th century. A form of it is used in the music of northern India.American composer Terry Riley also made use of the inverted form of it in his "Harp of New Albion". Just intonation gives superior results when there is little or no chord progression: voices and other instruments gravitate to just intonation whenever possible. However, it gives two different whole tone intervals (9:8 and 10:9) because a fixed tuned instrument, such as a piano, cannot change key.[14] To calculate the frequency of a note in a scale given in terms of ratios, the frequency ratio is multiplied by the tonic frequency. For instance, with a tonic of A4 (A natural above middle C), the frequency is 440 Hz, and a justly tuned fifth above it (E5) is simply 440×(3:2) = 660 Hz.
| Semitone | Ratio | Interval | Natural | Half Step |
|---|---|---|---|---|
| 0 | 1:1 | unison | 480 | 0 |
| 1 | 16:15 | minor semitone | 512 | 16:15 |
| 2 | 9:8 | major second | 540 | 135:128 |
| 3 | 6:5 | minor third | 576 | 16:15 |
| 4 | 5:4 | major third | 600 | 25:24 |
| 5 | 4:3 | perfect fourth | 640 | 16:15 |
| 6 | 45:32 | diatonic tritone | 675 | 135:128 |
| 7 | 3:2 | perfect fifth | 720 | 16:15 |
| 8 | 8:5 | minor sixth | 768 | 16:15 |
| 9 | 5:3 | major sixth | 800 | 25:24 |
| 10 | 9:5 | minor seventh | 864 | 27:25 |
| 11 | 15:8 | major seventh | 900 | 25:24 |
| 12 | 2:1 | octave | 960 | 16:15 |
The just major third, 5:4 and minor third, 6:5, are a syntonic comma, 81:80, apart from their Pythagorean equivalents 81:64 and 32:27 respectively. According to Carl Dahlhaus (1990, p. 187), "the dependent third conforms to the Pythagorean, the independent third to the harmonic tuning of intervals."
Western common practice music usually cannot be played in just intonation but requires a systematically tempered scale. The tempering can involve either the irregularities of well temperament or be constructed as a regular temperament, either some form of equal temperament or some other regular meantone, but in all cases will involve the fundamental features of meantone temperament. For example, the root of chord ii, if tuned to a fifth above the dominant, would be a major whole tone (9:8) above the tonic. If tuned a just minor third (6:5) below a just subdominant degree of 4:3, however, the interval from the tonic would equal a minor whole tone (10:9). Meantone temperament reduces the difference between 9:8 and 10:9. Their ratio, (9:8)/(10:9) = 81:80, is treated as a unison. The interval 81:80, called the syntonic comma or comma of Didymus, is the key comma of meantone temperament.
Equal temperament tunings
In equal temperament, the octave is divided into equal parts on the logarithmic scale. While it is possible to construct equal temperament scale with any number of notes (for example, the 24-tone Arab tone system), the most common number is 12, which makes up the equal-temperament chromatic scale. In western music, a division into twelve intervals is commonly assumed unless it is specified otherwise.For the chromatic scale, the octave is divided into twelve equal parts, each semitone (half-step) is an interval of the twelfth root of two so that twelve of these equal half steps add up to exactly an octave. With fretted instruments it is very useful to use equal temperament so that the frets align evenly across the strings. In the European music tradition, equal temperament was used for lute and guitar music far earlier than for other instruments, such as musical keyboards. Because of this historical force, twelve-tone equal temperament is now the dominant intonation system in the Western, and much of the non-Western, world.
Equally tempered scales have been used and instruments built using various other numbers of equal intervals. The 19 equal temperament, first proposed and used by Guillaume Costeley in the 16th century, uses 19 equally spaced tones, offering better major thirds and far better minor thirds than normal 12-semitone equal temperament at the cost of a flatter fifth. The overall effect is one of greater consonance. 24 equal temperament, with 24 equally spaced tones, is widespread in the pedagogy and notation of Arabic music. However, in theory and practice, the intonation of Arabic music conforms to rational ratios, as opposed to the irrational ratios of equally tempered systems.
While any analog to the equally tempered quarter tone is entirely absent from Arabic intonation systems, analogs to a three-quarter tone, or neutral second, frequently occur. These neutral seconds, however, vary slightly in their ratios dependent on maqam, as well as geography. Indeed, Arabic music historian Habib Hassan Touma has written that "the breadth of deviation of this musical step is a crucial ingredient in the peculiar flavor of Arabian music. To temper the scale by dividing the octave into twenty-four quarter-tones of equal size would be to surrender one of the most characteristic elements of this musical culture."
The following graph reveals how accurately various equal-tempered scales approximate three important harmonic identities: the major third (5th harmonic), the perfect fifth (3rd harmonic), and the "harmonic seventh" (7th harmonic). [Note: the numbers above the bars designate the equal-tempered scale (i.e., "12" designates the 12-tone equal-tempered scale, etc.)]
Note Frequency (Hz) Frequency
Distance from
previous noteLog frequency
log2 fLog frequency
Distance from
previous noteExact formula A2 110.00 N/A 6.781 N/A A♯2 116.54 6.54 6.864 0.0833 (or 1/12) B2 123.47 6.93 6.948 0.0833 C3 130.81 7.34 7.031 0.0833 C♯3 138.59 7.78 7.115 0.0833 D3 146.83 8.24 7.198 0.0833 D♯3 155.56 8.73 7.281 0.0833 E3 164.81 9.25 7.365 0.0833 F3 174.61 9.80 7.448 0.0833 F♯3 185.00 10.39 7.531 0.0833 G3 196.00 11.00 7.615 0.0833 G♯3 207.65 11.65 7.698 0.0833 A3 220.00 12.35 7.781 0.0833
Connections to Mathematics
Musical set theory uses the language of mathematical set theory in an elementary way to organize musical objects and describe their relationships. To analyze the structure of a piece of (typically atonal) music using musical set theory, one usually starts with a set of tones, which could form motives or chords. By applying simple operations such as transposition and inversion, one can discover deep structures in the music. Operations such as transposition and inversion are called isometries because they preserve the intervals between tones in a set.
Abstract algebra
Expanding on the methods of musical set theory, some theorists have used abstract algebra to analyze music. For example, the pitch classes in an equally tempered octave form an abelian group with 12 elements. It is possible to describe just intonation in terms of a free abelian group.Transformational theory is a branch of music theory developed by David Lewin. The theory allows for great generality because it emphasizes transformations between musical objects, rather than the musical objects themselves.
Theorists have also proposed musical applications of more sophisticated algebraic concepts. The theory of regular temperaments has been extensively developed with a wide range of sophisticated mathematics, for example by associating each regular temperament with a rational point on a Grassmannian.
The chromatic scale has a free and transitive action of the cyclic group , with the action being defined via transposition of notes. So the chromatic scale can be thought of as a torsor for the group .
Real and complex analysis
Real and complex analysis have also been made use of, for instance by applying the theory of the Riemann zeta function to the study of equal divisions of the octaveThe Riemann zeta function or Euler–Riemann zeta function, ζ(s), is a function of a complex variable s that analytically continues the sum of the Dirichlet series
As a function of a real variable, Leonhard Euler first introduced and studied it in the first half of the eighteenth century without using complex analysis, which was not available at the time. Bernhard Riemann's 1859 article "On the Number of Primes Less Than a Given Magnitude" extended the Euler definition to a complex variable, proved its meromorphic continuation and functional equation, and established a relation between its zeros and the distribution of prime numbers.[2]
The values of the Riemann zeta function at even positive integers were computed by Euler. The first of them, ζ(2), provides a solution to the Basel problem. In 1979 Apéry proved the irrationality of ζ(3). The values at negative integer points, also found by Euler, are rational numbers and play an important role in the theory of modular forms. Many generalizations of the Riemann zeta function, such as Dirichlet series, Dirichlet L-functions and L-functions, are known.

The Riemann zeta function ζ(z) represented in a rectangular region of the complex plane. It is generated as a Matplotlib plot using a version of the domain coloring method

A view of the Riemann zeta function showing the pole , and two zeros on the critical line.
The Riemann zeta function ζ(s) is a function of a complex variable s = σ + it. (The notation s, σ, and t is used traditionally in the study of the zeta function, following Riemann.)
The following infinite series converges for all complex numbers s with real part greater than 1, and defines ζ(s) in this case:
The Riemann zeta function is defined as the analytic continuation of the function defined for σ > 1 by the sum of the preceding series.
Leonhard Euler considered the above series in 1740 for positive integer values of s, and later Chebyshev extended the definition to Re(s) > 1.[3]
The above series is a prototypical Dirichlet series that converges absolutely to an analytic function for s such that σ > 1 and diverges for all other values of s. Riemann showed that the function defined by the series on the half-plane of convergence can be continued analytically to all complex values s ≠ 1. For s = 1 the series is the harmonic series which diverges to +∞, and
Specific values
For any positive even integer 2n:For odd positive integers, no such simple expression is known, although these values are thought to be related to the algebraic K-theory of the integers; see Special values of L-functions.
For nonpositive integers, one has
In particular, ζ vanishes at the negative even integers because Bm = 0 for all odd m other than 1.
Via analytic continuation, one can show that:
-
- This gives a way to assign a finite result to the divergent series 1 + 2 + 3 + 4 + ⋯, which has been used in certain contexts such as string theory.[4]
-
- Similarly to the above, this assigns a finite result to the series 1 + 1 + 1 + 1 + ⋯.
- (
 A059750)
A059750)
-
- This is employed in calculating of kinetic boundary layer problems of linear kinetic equations.[5]
-
- if we approach from numbers larger than 1. Then this is the harmonic series. But its Cauchy principal value
- exists which is the Euler–Mascheroni constant γ = 0.5772….
- if we approach from numbers larger than 1. Then this is the harmonic series. But its Cauchy principal value
- (
 A078434)
A078434)
-
- This is employed in calculating the critical temperature for a Bose–Einstein condensate in a box with periodic boundary conditions, and for spin wave physics in magnetic systems.
- (
 A013661)
A013661)
-
- The demonstration of this equality is known as the Basel problem. The reciprocal of this sum answers the question: What is the probability that two numbers selected at random are relatively prime?[6]
- (
 A002117)
A002117)
-
- This number is called Apéry's constant.
- (
 A0013662)
A0013662)
-
- This appears when integrating Planck's law to derive the Stefan–Boltzmann law in physics.
Euler product formula
The connection between the zeta function and prime numbers was discovered by Euler, who proved the identityThe Euler product formula can be used to calculate the asymptotic probability that s randomly selected integers are set-wise coprime. Intuitively, the probability that any single number is divisible by a prime (or any integer), p is 1/p. Hence the probability that s numbers are all divisible by this prime is 1/ps, and the probability that at least one of them is not is 1 − 1/ps. Now, for distinct primes, these divisibility events are mutually independent because the candidate divisors are coprime (a number is divisible by coprime divisors n and m if and only if it is divisible by nm, an event which occurs with probability 1/nm). Thus the asymptotic probability that s numbers are coprime is given by a product over all primes,
The functional equation
The Riemann zeta function satisfies the functional equation (known as the Riemann functional equation or Riemann's functional equation)The functional equation was established by Riemann in his 1859 paper "On the Number of Primes Less Than a Given Magnitude" and used to construct the analytic continuation in the first place. An equivalent relationship had been conjectured by Euler over a hundred years earlier, in 1749, for the Dirichlet eta function (alternating zeta function):
Riemann also found a symmetric version of the functional equation (which he denoted with the letter xi), given by first defining
Zeros, the critical line, and the Riemann hypothesis

Apart from the trivial zeros, the Riemann zeta function has no zeros to the right of σ = 1 and to the left of σ = 0 (neither can the zeros lie too close to those lines). Furthermore, the non-trivial zeros are symmetric about the real axis and the line σ = 1/2 and, according to the Riemann hypothesis, they all lie on the line σ = 1/2.
The Hardy–Littlewood conjectures
In 1914, Godfrey Harold Hardy proved that ζ(1/2 + it) has infinitely many real zeros.Hardy and John Edensor Littlewood formulated two conjectures on the density and distance between the zeros of ζ(1/2 + it) on intervals of large positive real numbers. In the following, N(T) is the total number of real zeros and N0(T) the total number of zeros of odd order of the function ζ(1/2 + it) lying in the interval (0, T].
- For any ε > 0, there exists a T0(ε) > 0 such that when
- For any ε > 0, there exists a T0(ε) > 0 and cε > 0 such that the inequality
- .
Zero-free region
The location of the Riemann zeta function's zeros is of great importance in the theory of numbers. The prime number theorem is equivalent to the fact that there are no zeros of the zeta function on the Re(s) = 1 line.[9] A better result[10] that follows from an effective form of Vinogradov's mean-value theorem is that ζ(σ + it) ≠ 0 whenever |t| ≥ 3 andOther results
It is known that there are infinitely many zeros on the critical line. Littlewood showed that if the sequence (γn) contains the imaginary parts of all zeros in the upper half-plane in ascending order, thenIn the critical strip, the zero with smallest non-negative imaginary part is 1/2 + 14.13472514…i (
Various properties
For sums involving the zeta-function at integer and half-integer values, see rational zeta series.Reciprocal
The reciprocal of the zeta function may be expressed as a Dirichlet series over the Möbius function μ(n):The Riemann hypothesis is equivalent to the claim that this expression is valid when the real part of s is greater than 1/2.
Universality
The critical strip of the Riemann zeta function has the remarkable property of universality. This zeta-function universality states that there exists some location on the critical strip that approximates any holomorphic function arbitrarily well. Since holomorphic functions are very general, this property is quite remarkable. The first proof of universality was provided by Sergei Mikhailovitch Voronin in 1975.[11] More recent work has included effective versions of Voronin's theorem[12] and extending it to Dirichlet L-functions.Estimates of the maximum of the modulus of the zeta function
Let the functions F(T;H) and G(s0;Δ) be defined by the equalitiesThe case H ≫ ln ln T was studied by Kanakanahalli Ramachandra; the case Δ > c, where c is a sufficiently large constant, is trivial.
Anatolii Karatsuba proved,[15][16] in particular, that if the values H and Δ exceed certain sufficiently small constants, then the estimates
The argument of the Riemann zeta function
The functionThere are some theorems on properties of the function S(t). Among those results[17][18] are the mean value theorems for S(t) and its first integral
- .
Representations
Dirichlet series
An extension of the area of convergence can be obtained by rearranging the original series.[19] The seriesMellin-type integrals
Starting with the integral formula one can show[20] by substitution and iterated differentation for natural
A similar Mellin transform involves the Riemann prime-counting function J(x), which counts prime powers pn with a weight of 1/n, so that
Theta functions
The Riemann zeta function can be given formally by a divergent Mellin transform[21]Laurent series
Integral
For all s ∈ ℂ, s ≠ 1 the integral relation (cf. Abel–Plana formula)Rising factorial
Another series development using the rising factorial valid for the entire complex plane is[citation needed]The Riemann zeta function also appears in a form similar to the Mellin transform in an integral over the Gauss–Kuzmin–Wirsing operator acting on xs − 1; that context gives rise to a series expansion in terms of the falling factorial.[23]
Hadamard product
On the basis of Weierstrass's factorization theorem, Hadamard gave the infinite product expansionLogarithmic derivative on the critical strip
Globally convergent series
A globally convergent series for the zeta function, valid for all complex numbers s except s = 1 + 2πin/ln 2 for some integer n, was conjectured by Konrad Knopp and proven by Helmut Hasse in 1930 (cf. Euler summation):Hasse also proved the globally converging series
Peter Borwein has shown a very rapidly convergent series suitable for high precision numerical calculations. The algorithm, making use of Chebyshev polynomials, is described in the article on the Dirichlet eta function.
Series representation at positive integers via the primorial[edit]
Series representation by the incomplete poly-Bernoulli numbers
The function ζ can be represented, for Re(s) > 1, by the infinite seriesn, ≥2 is an incomplete poly-Bernoulli number.[26]
Numerical algorithms
For , the Riemann zeta function has for fixed and for all the following representation in terms of three absolutely and uniformly converging series,[27]For a given argument with and one can approximate to any accuracy by summing the first series to , to and neglecting , if one chooses as the next higher integer of the unique solution of in the unknown , and from this . For one can neglect altogether. Under the mild condition one needs at most summands. Hence this algorithm is essentially as fast as the Riemann-Siegel formula. Similar algorithms are possible for Dirichlet L-functions.[27]
Applications
The zeta function occurs in applied statistics (see Zipf's law and Zipf–Mandelbrot law).Zeta function regularization is used as one possible means of regularization of divergent series and divergent integrals in quantum field theory. In one notable example, the Riemann zeta-function shows up explicitly in the calculation of the Casimir effect. The zeta function is also useful for the analysis of dynamical systems.[28]
Infinite series
The zeta function evaluated at equidistant positive integers appears in infinite series representations of a number of constants.[29]There are yet more formulas in the article Harmonic number.
Generalizations
There are a number of related zeta functions that can be considered to be generalizations of the Riemann zeta function. These include the Hurwitz zeta functionThe polylogarithm is given by
The Lerch transcendent is given by
The Clausen function Cls(θ) that can be chosen as the real or imaginary part of Lis(eiθ).
The multiple zeta functions are defined by
Fractional derivative
In the case of the Riemann zeta function, a difficulty is represented by the fractional differentiation in the complex plane. The Ortigueira generalization of the classical Caputo fractional derivative solves this problem. The α-order fractional derivative of the Riemann zeta function is given by [31]Systems for the twelve-note chromatic scale

Comparison of tunings: I IV V I.  Play just (help·info),
Play just (help·info),  Play Pythagorean (help·info),
Play Pythagorean (help·info),  Play meantone (help·info) (quarter-comma),
Play meantone (help·info) (quarter-comma),  Play well temperament (help·info) (Werckmeister), and
Play well temperament (help·info) (Werckmeister), and  Play equal temperament (help·info)
Play equal temperament (help·info)
Many different compromise methods are used to deal with this, each with its own characteristics, and advantages and disadvantages.
The main ones are:
Prelude No. 1, C major, BWV 846, from the Well-Tempered Clavier by Johann Sebastian Bach. Played in just intonation.
- In just intonation, the frequencies of the scale notes are related to one another by simple numeric ratios, a common example of this being 1:1, 9:8, 5:4, 4:3, 3:2, 5:3, 15:8, 2:1 to define the ratios for the seven notes in a C major scale. In this example, though many intervals are pure, the interval from D to A (5:3 to 9:8) is 40/27 instead of the expected 3/2. The same issue occurs with most just intonation tunings. This can be dealt with to some extent using alternative pitches for the notes. Even that, however, is only a partial solution, as an example makes clear: If one plays the sequence C G D A E C in just intonation, using the intervals 3/2, 3/4 and 5/4, then the second C in the sequence is higher than the first by a syntonic comma of 81/80. This is the infamous "comma pump". Each time around the comma pump, the pitch continues to spiral upwards. This shows that it is impossible to keep to any small fixed system of pitches if one wants to stack musical intervals this way. So, even with adaptive tuning, the musical context may sometimes require playing musical intervals that are not pure. Instrumentalists with the ability to vary the pitch of their instrument may micro-adjust some of the intervals naturally; there are also systems for adaptive tuning in software (microtuners). Harmonic fragment scales form a rare exception to this issue. In tunings such as 1:1 9:8 5:4 3:2 7:4 2:1, all the pitches are chosen from the harmonic series (divided by powers of 2 to reduce them to the same octave), so all the intervals are related to each other by simple numeric ratios.
- A Pythagorean tuning is technically a type of just intonation, in which the frequency ratios of the notes are all derived from the number ratio 3:2. Using this approach for example, the 12 notes of the Western chromatic scale would be tuned to the following ratios: 1:1, 256:243, 9:8, 32:27, 81:64, 4:3, 729:512, 3:2, 128:81, 27:16, 16:9, 243:128, 2:1. Also called "3-limit" because there are no prime factors other than 2 and 3, this Pythagorean system was of primary importance in Western musical development in the Medieval and Renaissance periods. As with nearly all just intonation systems, it has a wolf interval. In the example given, it is the interval between the 729:512 and the 256:243 (F♯ to D♭, if one tunes the 1/1 to C). The major and minor thirds are also impure, but at the time when this system was at its zenith, the third was considered a dissonance, so this was of no concern. See also: Shí-èr-lǜ.
- A system of tuning that averages out pairs of ratios used for the same interval (such as 9:8 and 10:9). The best known form of this temperament is quarter-comma meantone, which tunes major thirds justly in the ratio of 5:4 and divides them into two whole tones of equal size – this is achieved by flattening the fifths of the Pythagorean system slightly (by a quarter of a syntonic comma). However, the fifth may be flattened to a greater or lesser degree than this and the tuning system retains the essential qualities of meantone temperament. Historical examples include 1/3-comma and 2/7-comma meantone.
- Any one of a number of systems where the ratios between intervals are unequal, but approximate to ratios used in just intonation. Unlike meantone temperament, the amount of divergence from just ratios varies according to the exact notes being tuned, so that C-E is probably tuned closer to a 5:4 ratio than, say, D♭-F. Because of this, well temperaments have no wolf intervals.
- The standard twelve-tone equal temperament is a special case of meantone temperament (extended eleventh-comma), in which the twelve notes are separated by logarithmically equal distances (100 cents): A harmonized C major scale in equal temperament (.ogg format, 96.9KB). This is the most common tuning system used in Western music, and is the standard system used as a basis for tuning a piano. Since this scale divides an octave into twelve equal-ratio steps and an octave has a frequency ratio of two, the frequency ratio between adjacent notes is then the twelfth root of two, 21/12, or ~1.05946309.... However, the octave can be divided into other than 12 equal divisions, some of which may be more harmonically pleasing as far as thirds and sixths are concerned, such as 19 equal temperament (extended third-comma meantone), 31 equal temperament (extended quarter-comma meantone) and 53 equal temperament (extended Pythagorean tuning).
- Any of a number of systems that construct the twelve tone system as a cycle of twelve equal tempered fifths. If you use seven equal tempered fifths, the result is one of the regular diatonic tunings with tone and semitone in the pattern TTSTTTS (or a rotation of it) with the S smaller than the T. When you continue the cycle to twelve tempered fifths, the result is CDCDDCDCDCDD (or a rotation of it) where C is the chromatic semitone and D is the diatonic semitone. Depending on the ratio of C to D the result can be a subset of an equal temperament of more than 12 notes. For instance, if D = 2*C the result is a twelve note subset of nineteen equal which closely approximates 1/3 comma meantone and if C = (2/3)*D the result is twelve note subset of thirty one equal which closely approximate 1/4 comma meantone.
- Tempered timbres
- A timbre's partials (also known as harmonics or overtones) can be tempered such that each of the timbre's partials aligns with a note of a given tempered tuning. This alignment of tuning and timbre is a key component in the perception of consonance,[2] of which one notable example is the alignment between the partials of a harmonic timbre and a just intonation tuning. Hence, using tempered timbres, one can achieve a degree of consonance, in any tempered tuning, that is comparable to the consonance achieved by the combination of just intonation tuning and harmonic timbres. Tempering timbres in real time, to match a tuning that can change smoothly in real time, using the tuning-invariant fingering of an isomorphic keyboard, is a central component of dynamic tonality.
Electronic tuner
In music, an electronic tuner is a device that detects and displays the pitch of musical notes played on a musical instrument. "Pitch" is the highness or lowness of a musical note, which is typically measured in Hertz. Simple tuners indicate—typically with an analog needle-dial, LEDs, or an LCD screen—whether a pitch is lower, higher, or equal to the desired pitch. In the 2010s, software applications can turn a smartphone, tablet, or personal computer into a tuner. More complex and expensive tuners indicate pitch more precisely. Tuners vary in size from units that fit in a pocket to 19" rack-mount units. Instrument technicians, piano tuners, and violin-family luthiers typically use more expensive, accurate tuners.[1]
The simplest tuners detect and display tuning only for a single pitch—often "A" or "E"—or for a small number of pitches, such as the six used in the standard tuning of a guitar (E,A,D,G,B,E). More complex tuners offer chromatic tuning for all 12 pitches of the equally tempered octave. Some electronic tuners offer additional features, such as pitch calibration, temperament options, the sounding of a desired pitch through an amplifier plus speaker, and adjustable "read-time" settings that affect how long the tuner takes to measure the pitch of the note.
Among the most accurate tuning devices, strobe tuners work differently than regular electronic tuners. They are stroboscopes that flicker a light at the same frequency as the note. The light shines on a wheel that spins at a precise speed. The interaction of the light and regularly-spaced marks on the wheel creates a stroboscopic effect that makes the marks for a particular pitch appear to stand still when the pitch is in tune. These can tune instruments and audio devices more accurately than most non-strobe tuners. However, mechanical strobe units are expensive and delicate, and their moving parts require periodic servicing, so they are used mainly in applications that require higher precision, such as by professional instrument makers and repair experts.

Pocket-sized Korg chromatic LCD tuner, with simulated analog indicator needle
Regular electronic tuners contain either an input jack for electric instruments (usually a 1/4" patch cord input), a microphone, or a clip-on sensor (e.g., a piezoelectric pickup) or some combination of these inputs. Pitch detection circuitry drives some type of display (an analog needle, an LCD simulated image of a needle, LED lights, or a spinning translucent disk illuminated by a strobing backlight). Some tuners have an output, or through-put, so the tuner can connect 'in-line' from an electric instrument to an instrument amplifier or mixing console. Small tuners are usually battery powered. Many battery powered tuners also have a jack for an optional AC power supply.

Some rock and pop guitarists and bassists use "stompbox" format electronic tuners that route the electric signal for the instrument through the unit via a 1/4" patch cable. These pedal-style tuners usually have an output so that the signal can be plugged into a guitar amp.
"Clip-on" tuners typically attach to instruments with a spring-loaded clip that has a built-in contact microphone. Clipped onto a guitar headstock or violin scroll, these sense pitch even in loud environments, for example when other people are tuning.
Some guitar tuners fit into the instrument itself. Typical of these are the Sabine AX3000 and the "NTune" device. The NTune consists of a switching potentiometer, a wiring harness, illuminated plastic display disc, a circuit board and a battery holder. The unit installs in place of an electric guitar's existing volume knob control. The unit functions as a regular volume knob when not in tuner mode. To operate the tuner, the player pulls the volume knob up. The tuner disconnects the guitar's output so the tuning process is not amplified. The lights on the illuminated ring, under the volume knob, indicate the note being tuned. When the note is in tune a green "in tune" indicator light illuminates. After tuning is complete the musician pushes the volume knob back down, disconnecting the tuner from the circuit and re-connecting the pickups to the output jack.
Gibson guitars released a guitar model in 2008 called the Robot Guitar—a customized version of either the Les Paul or SG model. The guitar is fitted with a special tailpiece with in-built sensors that pick up the frequency of the strings. An illuminated control knob selects different tunings. Motorized tuning machines on the headstock automatically tune the guitar. In "intonation" mode, the device displays how much adjustment the bridge requires with a system of flashing LEDs on the control knob.
J.D. Richard invented the first automated guitar tuner in 1982 while studying electrical engineering at the University of New Brunswick, New Brunswick Canada. This tuner was based on a phase-locked-looped feedback design that monitored the frequency of the string and turned a stepper motor (with a 400/1 gear ratio) attached to the tuning peg of the guitar. The design never went into production, though the thesis paper is still available at the university.
Regular needle, LCD and LED display tuners
A needle, LCD or regular LED type tuner uses a microprocessor to measure the average period of the waveform. It uses that information to drive the needle or array of lights. When the musician plays a single note, the tuner senses the pitch. The tuner then displays the pitch in relation to the desired pitch, and indicates whether the input pitch is lower, higher, or equal to the desired pitch. With needle displays, the note is in tune when the needle is in a 90° vertical position, with leftward or rightward deviations indicating that the note is flat or sharp, respectively. Tuners with a needle are often supplied with a backlight, so that the display can be read on a darkened stage.For block LED or LCD display tuners, markings on the readout drift left if the note is flat and right if the note is sharp from the desired pitch. If the input frequency is matched to the desired pitch frequency the LEDs are steady in the middle and an 'in tune' reading is given.
Some LCDs mimic needle tuners with a needle graphic that moves in the same way as a genuine needle tuner. Somewhat misleadingly, many LED displays have a 'strobe mode' that mimics strobe tuners by scrolling the flashing of the LEDs cyclically to simulate the display of a true strobe. However, these are all just display options. The way a regular tuner 'hears' and compares the input note to a desired pitch is exactly the same, with no change in accuracy. For more on how strobe tuners work see the dedicated section.
The least expensive models only detect and display a small number of pitches, often those pitches that are required to tune a given instrument (e.g., E, A, D, G, B, E of standard guitar tuning). While this type of tuner is useful for bands that only use stringed instruments such as guitar and electric bass, it is not that useful for tuning brass or woodwind instruments. Tuners at the next price point offer chromatic tuning, the ability to detect and assess all the pitches in the chromatic scale (e.g., C, C♯, D, D♯, etc.). Chromatic tuners can be used for B♭ and E♭ brass instruments, such as saxophones and horns. Many models have circuitry that automatically detects which pitch is being played, and then compares it against the correct pitch. Less expensive models require the musician to specify the target pitch via a switch or slider. Most low- and mid-priced electronic tuners only allow tuning to an equal temperament scale.
Electric guitar and electric bass players who perform concerts may use electronic tuners built into an effects pedal, often called a stomp box. These tuners have a rugged metal or heavy-duty plastic housing and a foot-operated switch to toggle between the tuner and a bypass mode. Professional guitarists may use a more expensive version of the LED tuner mounted in a rack-mount case with a larger range of LEDs for more accurate pitch display. Many models let the user select reference pitches other than A440. On many electronic tuners, the user can select a different note—useful for, for example, dropping a guitar's tuning to a lower pitch (e.g., Dropped tuning). Some models are adjustable standards other than A=440. This is useful to some Baroque musicians who play period instruments at lower reference pitches—such as A=435. Some higher-priced electronic tuners support tuning to a range of different temperaments—a feature useful to some guitarists and harpsichord players.
Some expensive tuners also include an on-board speaker that can sound notes, either to facilitate tuning by ear or to act as a pitch reference point for intonation practice. Some expensive tuners provide an adjustable read time that controls at what time interval the circuitry assesses pitch. The combination of all the above features makes some tuners preferable for tuning instruments in an orchestra. These are sometimes called "orchestral tuners".
Clip-on
Apps
Many chromatic and guitar tuner apps are available for Android and iOS smartphones. Many are free to download and install.Strobe tuners
Strobe tuners (the popular term for stroboscopic tuners) are the most accurate type of tuner. There are three types of strobe tuners: the mechanical rotating disk strobe tuner, an LED array strobe in place of the rotating disk, and "virtual strobe" tuners with LCDs or ones that work on personal computers. A strobe tuner shows the difference between a reference frequency and the musical note being played. Even the slightest difference between the two shows up as a rotating motion in the strobe display. The accuracy of the tuner is only limited by the internal frequency generator. The strobe tuner detects the pitch either from a TRS input jack or a built-in or external microphone connected to the tuner.The first strobe tuner dates back to 1936 and was originally made by the Conn company; it was called the Stroboconn and was produced for approximately 40 years. However, these strobes are now mainly collector pieces. They had 12 strobe discs, driven by one motor. The gearing between discs was a very close approximation to the 12th root of two ratio. This tuner had an electrically driven temperature-compensated tuning fork; the electrical output of this fork was amplified to run the motor. The fork had sliding weights, an adjustment knob, and a dial to show the position of the weights. These weights permitted setting it to different reference frequencies (such as A4 = 435 Hz), although over a relatively narrow range, perhaps a whole tone. When set at A4 = 440 Hz the tuning fork produced a 55 Hz signal, which drove the four-pole 1650 RPM synchronous motor to which the A disc was mounted. (The other discs were all gear-driven off of this one.) Incoming audio was amplified to feed a long neon tube common to all 12 discs. Wind instrument repair people liked this tuner because it needed no adjustment to show different notes. Anyone who had to move this tuner around was less inclined to like it because of its size and weight: two record-player-sized cases of 30-40 pounds each.
How it works
Mechanical strobe tuners have a series of lamps or LEDs powered by amplified audio from the instrument; they flash (or strobe) at the same frequency as the input signal. For instance an 'A' played on a guitar's 6th string at the 5th fret has the frequency of 110 Hz when in tune. An 'A' played on the 1st string at the 5th fret vibrates at 440 Hz. As such, the lamps would flash either 110 or 440 times per second in the above examples. In front of these flashing lights is a motor-driven, translucent printed disc with rings of alternating transparent and opaque sectors.This disc rotates at a fixed specific speed, set by the user. Each disc rotation speed is set to a particular frequency of the desired note. If the note being played (and making the lamps behind the disc flash) is at exactly the same frequency as the spinning of the disc, then the disc appears to be static (due to the persistence of vision) from the strobing effect. If the note is out of tune then the pattern appears to be moving as the light flashing and the disc rotation are out of sync from each other. The more out of tune the played note is, the faster the pattern seems to be moving, although in reality it always spins at the same speed for a given note. Many good turntables for vinyl disc records have stroboscopic patterns lit by the incoming AC power (mains). The power frequency, either 50 or 60 Hz, serves as the reference, although commercial power frequency sometimes changes slightly (a few tenths of a percent) with varying load. Unless reference and measured quantity are interchanged, the operating principle is the same; the turntable speed is adjusted to stop drifting of the pattern.
As the disc has multiple bands, each with different spacings, each band can be read for different partials within one note. As such, extremely fine tuning can be obtained, because the user can tune to a particular partial within a given note. This is impossible on regular needle, LCD or LED tuners. The strobe system is about 30 times more accurate than a quality electronic tuner, being accurate to 1/10 of a cent. Advertisements for the Sonic Research LED strobe claim that it is calibrated to ± 0.0017 cents and guaranteed to maintain an accuracy of ± 0.02 cents or 1/50 of a cent.
Strobe units can often be calibrated for many tunings and preset temperaments and allow for custom temperament programming, stretched tuning, "sweetened" temperament tunings and Buzz Feiten tuning modifications. Due to their accuracy and ability to display partials even on instruments with a very short "voice" (e.g., notes of short duration), strobe tuners can perform tuning tasks that would be very difficult, if not impossible, for needle-type tuners. For instance, needle/LED display type tuners cannot track the signal to identify a tone of the Caribbean steelpan (often nicknamed the "steeldrum") due to its very short "voice". A tuner needs to be able to detect the first few partials for tuning such an instrument, which means that only a strobe tuner can be used for steelpan tuning. This is also true of the comb teeth used in mechanical musical instruments like Music Boxes and the like. In such cases a technician has to physically remove metal from the tooth to reach the desired note. The metal teeth only resonates briefly when plucked. Great accuracy is required as once the metal is cut or filed away, the lost material cannot be replaced. As such, the strobe-type tuners are the unit of choice for such tasks. Tuners with an accuracy of better than 0.2 cent are required for guitar intonation tuning.
One of the most expensive strobe tuners is the Peterson Strobe Center, which has twelve separate mechanical strobe displays; one for each pitch of the equally tempered octave. This unit (about $3,500 US) can tune multiple notes of a sound or chord, displaying each note's overtone sub-structure simultaneously. This gives an overall picture of tuning within a sound, note or chord that is not possible with most other tuning devices. (The TC Electronic Polytune can display the pitch accuracy of up to six pre-selected notes.) It is often used for tuning complex instruments and sound sources, or difficult-to-tune instruments where the technician requires a very accurate and complete aural picture of an instrument's output. For instance, when tuning musical bells, this model displays several of the bell's partials (hum, second partial, tierce, quint and nominal/naming note) as well as the prime, and each of their partials, on separate displays. The unit is heavy and fragile, and requires a regular maintenance schedule. Each of the twelve displays requires periodic re-calibration. It can be used to teach students about note substructures, which show on the separate strobing displays.
Strobe developments
Mechanical disc strobe tuners are expensive, bulky, delicate, and require periodic maintenance (keeping the motor that spins the disc at the correct speed, replacing the strobing LED backlight, etc.). For many, a mechanical strobe tuner is simply not practical for one or all of the above reasons. To address these issues, in 2001 Peterson Tuners added a line of non-mechanical electronic strobe tuners that have LCD dot-matrix displays mimicking a mechanical strobe disc display, giving a stroboscopic effect. In 2004 Peterson made a model of LCD strobe in a sturdy floor based "stomp box" for live on-stage use. Virtual strobe tuners are as accurate as standard mechanical disc strobe tuners. However, there are limitations to the virtual system compared to the disc strobes. Virtual strobes display fewer bands to read note information, and do not pick up harmonic partials like a disc strobe. Rather, each band on a virtual strobe represents octaves of the fundamental. A disc strobe provides "one band correspondence"—each band displays a particular frequency of the note being played. On the virtual strobe system, each band combines a few close frequencies for easier reading on the LCD. This is still extremely accurate for intoning and tuning most instruments—but, as of this writing, no virtual strobe tuner provides detailed information on partials.Sonic Research and Planet Waves both released a true-strobe with a bank of LEDs arranged in a circle that gives a strobing effect based upon the frequency of the input note. Both LCD and LED display true strobes do not require mechanical servicing and are much cheaper than the mechanical types. As such, they are a popular option for musicians who want the accuracy of a strobe without the high cost and the maintenance requirements. However, LED strobe displays offer no information about the harmonic structure of a note, unlike LCD types, which do offer four bands of consolidated information.
As both mechanical and electronic strobes are still more expensive and arguably more difficult to use in order to achieve the desired results than ordinary tuners, their use is usually limited to those whose business it is accurately to intone and tune pianos, harps, and early instruments (e. g. harpsichords) on a regular basis: luthiers, instrument restorers and technicians – and instrument enthusiasts. These tuners make the intonation process more precise.
Uses
Classical music
In classical music, there is a longstanding tradition to tune "by ear", by adjusting the pitch of instruments to a reference pitch. In an orchestra, the oboe player gives a 440 Hz "A", and the different instrument sections tune to this note. In chamber music, either one of the woodwind players gives an "A", or if none is present, one of the string players, usually the first violinist, bows his or her open "A" string. If an orchestra is accompanying a piano concerto, the first oboist takes the "A" from the piano and then plays this pitch for the rest of the orchestra (a somewhat unscientific procedure, but consecrated by longstanding usage).Despite this tradition of tuning by ear, electronic tuners are still widely used in classical music. In orchestras the oboist often uses a high-end electronic tuner to ensure that her/his "A" is correct. As well, other brass or woodwind players may use electronic tuners to ensure that their instruments are correctly tuned. Classical performers also use tuners off-stage for practice purposes or to check their tuning (or, with the further aid of a speaker, to practice ear training). Electronic tuners are also used in opera orchestras for offstage trumpet effects. In offstage trumpet effects, trumpet players performs a melody from the backstage or from a hallway behind the stage, creating a haunting, muted effect. Since trumpet players cannot hear the orchestra, they cannot know whether or not their notes are in tune with the rest of the ensemble; to resolve this problem, some trumpet players use a high-end, sensitive tuner so that they can monitor the pitch of their notes.
Piano tuners, harp makers and the builders and restorers of early instruments, e.g. harpsichords, use high-end tuners to assist with their tuning and instrument building. Even piano tuners who work mostly "by ear" may use an electronic tuner to tune just a first key on the piano, e. g. the a' to 440 Hz, after which they proceed by means of octaves, approximate fifths and approximate fourths to tune the others. (In the twelve-tone equal temperament system dominant in classical and Western music, all intervals except the octave are slightly "mistuned" or compromised compared to more consonant just intervals.) They may also use electronic tuners to get a very out-of-tune piano roughly in pitch, after which point they tune by ear. Electronic tuning devices for keyboard instruments are for various reasons generally much more complex and therefore expensive than in the case of other widely used instruments.
Popular and folk music
In popular music, amateur and professional bands from styles as varied as country and heavy metal use electronic tuners to ensure that the guitars and electric bass are correctly tuned. In popular music genres such as rock music, there is a great deal of stage volume due to the use of drums and guitar amplifiers, so it can be difficult to tune "by ear". Electronic tuners are helpful aids at jam sessions where a number of players are sharing the stage, because it helps all of the players to have their instruments tuned to the same pitch, even if they have come to the session halfway through. Tuners are helpful with acoustic instruments, because they are more affected by temperature and humidity changes. An acoustic guitar or upright bass that is perfectly in tune backstage can change in pitch under the heat of the stage lights and from the humidity from thousands of audience members.Tuners are used by guitar technicians who are hired by rock and pop bands to ensure that all of the band's instruments are ready to play at all times. Guitar technicians (often called guitar techs) tune all of the instruments (electric guitars, electric basses, acoustic guitars, mandolins, etc.) before the show, after they are played, and before they are used onstage. Guitar techs also retune instruments throughout the show. Whereas amateur musicians typically use a relatively inexpensive quartz tuner, guitar technicians typically use expensive, high-end tuners such as strobe tuners. Most strobe tuners, counter-intuitively, also use quartz crystal oscillators as time references, although the responses are processed differently by the different units.
Bell tuning
Strobe tuners are used in the tuning of bells, which require accurate tuning of many partials. The removal of metal from various parts of the bell shape is by a tuning lathe, and once too much metal has been removed it cannot be reversed. Hence accurate approach to the desired tuning partial is essential to prevent overshoot .
Sound synthesis
Additive synthesis builds sounds by adding together waveforms into a composite sound. Instrument sounds are simulated by matching their natural harmonic overtone structure. Early analog examples of additive synthesizers are the Teleharmonium, Hammond organ, and Synclavier.
Phase distortion synthesis is a method implemented on Casio CZ synthesizers. It replaces the traditional analog waveform with a choice of several digital waveforms which are more complex than the standard square, sine, and sawtooth waves. This waveform is routed to a digital filter and digital amplifier, each modulated by an eight stage envelope. The sound can then be further modified with ring modulation or noise modulation.
Analysis/resynthesis is a form of synthesis that uses a series of bandpass filters or Fourier transforms to analyze the harmonic content of a sound. The results are then used to resynthesize the sound using a band of oscillators. The vocoder, linear predictive coding, and some forms of speech synthesis are based on analysis/resynthesis.
Imitative synthesis
Sound synthesis can be used to mimic acoustic sound sources. Generally, a sound that does not change over time includes a fundamental partial or harmonic, and any number of partials. Synthesis may attempt to mimic the amplitude and pitch of the partials in an acoustic sound source.When natural sounds are analyzed in the frequency domain (as on a spectrum analyzer), the spectra of their sounds exhibits amplitude spikes at each of the fundamental tone's harmonics corresponding to resonant properties of the instruments (spectral peaks that are also referred to as formants). Some harmonics may have higher amplitudes than others. The specific set of harmonic-vs-amplitude pairs is known as a sound's harmonic content. A synthesized sound requires accurate reproduction of the original sound in both the frequency domain and the time domain. A sound does not necessarily have the same harmonic content throughout the duration of the sound. Typically, high-frequency harmonics die out more quickly than the lower harmonics.
In most conventional synthesizers, for purposes of re-synthesis, recordings of real instruments are composed of several components representing the acoustic responses of different parts of the instrument, the sounds produced by the instrument during different parts of a performance, or the behavior of the instrument under different playing conditions (pitch, intensity of playing, fingering, etc.)
Component
- Electronic oscillators – create raw sounds with a timbre that depends upon the waveform generated. Voltage-controlled oscillators (VCOs) and digital oscillators may be used. Harmonic additive synthesis models sounds directly from pure sine waves, somewhat in the manner of an organ, while frequency modulation and phase distortion synthesis use one oscillator to modulate another. Subtractive synthesis depends upon filtering a harmonically rich oscillator waveform. Sample-based and granular synthesis use one or more digitally recorded sounds in place of an oscillator.
- Low frequency oscillator (LFO) – an oscillator of adjustable frequency that can be used to modulate the sound rhythmically, for example to create tremolo or vibrato or to control a filter's operating frequency. LFOs are used in most forms of synthesis.
- Voltage-controlled filter (VCF) – "shape" the sound generated by the oscillators in the frequency domain, often under the control of an envelope or LFO. These are essential to subtractive synthesis.
- ADSR envelopes – provide envelope modulation to "shape" the volume or harmonic content of the produced note in the time domain with the principal parameters being attack, decay, sustain and release. These are used in most forms of synthesis. ADSR control is provided by envelope generators.
- Voltage-controlled amplifier (VCA) – After the signal generated by one (or a mix of more) VCOs has been modified by filters and LFOs, and its waveform has been shaped (contoured) by an ADSR envelope generator, it then passes on to one or more voltage-controlled amplifiers (VCAs). A VCA is a preamp that boosts (amplifies) the electronic signal before passing it on to an external or built-in power amplifier, as well as a means to control its amplitude (volume) using an attenuator. The gain of the VCA is affected by a control voltage (CV), coming from an envelope generator, an LFO, the keyboard or some other source.[80]
- Other sound processing effects such as ring modulators may be encountered.
Filter
Electronic filters are particularly important in subtractive synthesis, being designed to pass some frequency regions through unattenuated while significantly attenuating ("subtracting") others. The low-pass filter is most frequently used, but band-pass filters, band-reject filters and high-pass filters are also sometimes available.The filter may be controlled with a second ADSR envelope. An "envelope modulation" ("env mod") parameter on many synthesizers with filter envelopes determines how much the envelope affects the filter. If turned all the way down, the filter produces a flat sound with no envelope. When turned up the envelope becomes more noticeable, expanding the minimum and maximum range of the filter.
Attack Decay Sustain Release (ADSR) envelope
| Key | on | off | |||
- Attack time is the time taken for initial run-up of level from nil to peak, beginning when the key is first pressed.
- Decay time is the time taken for the subsequent run down from the attack level to the designated sustain level.
- Sustain level is the level during the main sequence of the sound's duration, until the key is released.
- Release time is the time taken for the level to decay from the sustain level to zero after the key is released.
Some electronic musical instruments can invert the ADSR envelope, reversing the behavior of the normal ADSR envelope. During the attack phase, the modulated sound parameter fades from the maximum amplitude to zero then, during the decay phase, rises to the value specified by the sustain parameter. After the key has been released the sound parameter rises from sustain amplitude back to maximum amplitude.
8-step envelope on Casio CZ series
Certain synthesizers also allow for a delay parameter before the attack. Modern synthesizers like the Dave Smith Instruments Prophet '08 have DADSR (delay, attack, decay, sustain, release) envelopes. The delay setting determines the length of silence between hitting a note and the attack. Some software synthesizers, such as Image-Line's 3xOSC (included with their DAW FL Studio) have DAHDSR (delay, attack, hold, decay, sustain, release) envelopes.
A common feature on many synthesizers is an AD envelope (attack and decay only). This can be used to control e.g. the pitch of one oscillator, which in turn may be synchronized with another oscillator by oscillator sync.
LFO
LFO section of Access Virus C
Arpeggiator
An arpeggiator (arp) is a feature available on several synthesizers that automatically steps through a sequence of notes based on an input chord, thus creating an arpeggio. The notes can often be transmitted to a MIDI sequencer for recording and further editing. An arpeggiator may have controls for speed, range, and order in which the notes play; upwards, downwards, or in a random order. More advanced arpeggiators allow the user to step through a pre-programmed complex sequence of notes, or play several arpeggios at once. Some allow a pattern sustained after releasing keys: in this way, a sequence of arpeggio patterns may be built up over time by pressing several keys one after the other. Arpeggiators are also commonly found in software sequencers. Some arpeggiators/sequencers expand features into a full phrase sequencer, which allows the user to trigger complex, multi-track blocks of sequenced data from a keyboard or input device, typically synchronized with the tempo of the master clock. An arpeggiator interface on Novation Nova |
Trance Lead
A sample of Eurodance synthesizer riff with use of rapid 1/16 notes arpeggiator
|
Arpeggiators seem to have grown from the accompaniment system used in electronic organs in the mid-1960s to the mid-1970s.[84] They were also commonly fitted to keyboard instruments through the late 1970s and early 1980s. Notable examples are the RMI Harmonic Synthesizer (1974),[85] Roland Jupiter-8, Oberheim OB-8, Roland SH-101, Sequential Circuits Six-Trak and Korg Polysix. A famous example can be heard on Duran Duran's song "Rio", in which the arpeggiator on a Roland Jupiter-4 plays a C minor chord in random mode. They fell out of favor by the latter part of the 1980s and early 1990s and were absent from the most popular synthesizers of the period but a resurgence of interest in analog synthesizers during the 1990s, and the use of rapid-fire arpeggios in several popular dance hits, brought with it a resurgence.
Patch
One of the earliest patch memory (bottom left) on Oberheim Four-voice (1975/1976)
In mid–late 1970s, patch memory (allowing storage and loading of 'patches' or 'programs') began to appear in synths like the Oberheim Four-voice (1975/1976)[86] and Sequential Circuits Prophet-5 (1977/1978). After MIDI was introduced in 1983, more and more synthesizers could import or export patches via MIDI SYSEX commands. When a synthesizer patch is uploaded to a personal computer that has patch editing software installed, the user can alter the parameters of the patch and download it back to the synthesizer. Because there is no standard patch language, it is rare that a patch generated on one synthesizer can be used on a different model. However, sometimes manufacturers design a family of synthesizers to be compatible.
Control interfaces
Tangible interface (Reactable)
Guitar-style interface (SynthAxe)
- Fingerboards (ribbon controllers) and touchpads
- Wind controllers
- Guitar-style interfaces
- Drum pads
- Music sequencers
- Non-contact interfaces akin to theremins
- Tangible interfaces like a Reactable, AudioCubes
- Various auxiliary input device including: wheels for pitch bend and modulation, footpedals for expression and sustain, breath controllers, beam controllers, etc.
Fingerboard controller
Fingerboard-controlled instruments include the Trautonium (1929), Hellertion (1929) and Heliophon (1936),[94][95][96] Electro-Theremin (Tannerin, late 1950s), Persephone (2004), and the Swarmatron (2004). A ribbon controller is used as an additional controller in the Yamaha CS-80 and CS-60, the Korg Prophecy and Korg Trinity series, the Kurzweil synthesizers, Moog synthesizers, and others.
Rock musician Keith Emerson used it with the Moog modular synthesizer from 1970 onward. In the late 1980s, keyboards in the synth lab at Berklee College of Music were equipped with membrane thin ribbon style controllers that output MIDI. They functioned as MIDI managers, with their programming language printed on their surface, and as expression/performance tools. Designed by Jeff Tripp of Perfect Fretworks Co., they were known as Tripp Strips. Such ribbon controllers can serve as a main MIDI controller instead of a keyboard, as with the Continuum instrument.
Wind controllers
Wind controllers (and wind synthesizers) are convenient for woodwind and brass players, being designed to imitate those instruments. These are usually either analog or MIDI controllers, and sometimes include their own built-in sound modules (synthesizers). In addition to the follow of key arrangements and fingering, the controllers have breath-operated pressure transducers, and may have gate extractors, velocity sensors, and bite sensors. Saxophone-style controllers have included the Lyricon, and products by Yamaha, Akai, and Casio. The mouthpieces range from alto clarinet to alto saxophone sizes. The Eigenharp, a controller similar in style to a bassoon, was released by Eigenlabs in 2009. Melodica and recorder-style controllers have included the Martinetta (1975)[97] and Variophon (1980),[98] and Joseph Zawinul's custom Korg Pepe.[99] A harmonica-style interface was the Millionizer 2000 (c. 1983).[100]Trumpet-style controllers have included products by Steiner/Crumar/Akai, Yamaha, and Morrison. Breath controllers can also be used to control conventional synthesizers, e.g. the Crumar Steiner Masters Touch,[101] Yamaha Breath Controller and compatible products.[102] Several controllers also provide breath-like articulation capabilities.
Accordion controllers use pressure transducers on bellows for articulation.
======================== electronic tuner =======================


















































































![{\displaystyle H{\sqrt[{3}]{\ln T}}e^{-c{\sqrt {\ln \ln T}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2a08b909b3fbdc065cdc21c25e4469fb8136817)




































![{\displaystyle {\begin{aligned}\zeta \left(s\right)&=\sum _{n=1}^{\infty }n^{-s}\sum _{w=0}^{v-1}{\frac {\left({\frac {n}{N}}\right)^{w}}{w!}}e^{-{\frac {n}{N}}}-{\frac {\Gamma \left(1-s+v\right)}{\left(1-s\right)\Gamma \left(v\right)}}N^{1-s}+\sum _{\mu =\pm 1}E_{\mu }\left(s\right)\\E_{\mu }\left(s\right)&=\left(2\pi \right)^{s-1}\Gamma \left(1-s\right)e^{i\mu {\frac {\pi }{2}}\left(1-s\right)}\sum _{m=1}^{\infty }\left[m^{s-1}-\sum _{w=0}^{v-1}{\binom {s-1}{w}}\left(m+{\frac {i\mu }{2\pi N}}\right)^{s-1-w}\left({\frac {-i\mu }{2\pi N}}\right)^{w}\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b3556f6f9dd5d528740f31309d29c6aba64aacc)