In simple electronics locking and memory are translated with simple flip flop circuits as a source of energy and time on the book bit accumulator technique.
The flip flop is examined in three types of book bit projections: monostable, bistable and astable, within the scope of the continuum projection accumulator .

xample ;

Flip-flop 2 transistors are a series of 2 transistor combinations that each work as a switch and will be active alternately continuously. Since the two flip-flop transistors always have two continuous states on both transistors, the flip-flop 2 transistor is called an astable multivibrator (Astable Multivibrator) or also called a fre running multivibrator. The condition of the two states in the two intercurrent transistors occurs as a feedback network is installed between the two transistors using a capacitor connected between the base TR1 with the collector TR2 and the base TR2 with the collector TR1.

Rangkaian Flip Flop 2 Transistor (Astabil Multivibrator),flip flop 2 transistor,free running multivibrator,astabil multivibrator,free running multivibrator 2 transistor,teori flip flop 2 transistor,konfigurasi flip-flop 2 transistor,prinsip kerja flip-flop 2 transistor,rangkaian flip flop 2 transistor,output flip-flop 2 transistor,rangkaian free running multivibrator,prinsip kerja free running multivibrator,teori free running multivibrator,ouptu free running multivibrator,frekuensi free running multivibrator,rangkaian astabil multivibrator,teori astabil multivibrator transistor,prinsip kerja astabil multivibrator transistor,astable multivibrator,astable multivibrator transistor,teori astable multivibrator transistor,prinsip kerja astable multivibrator

What makes this flip-flop circuit 2 transistors have two alternating conditions between cut-off and saturation is the RC circuit on both transistors. The process of occurrence of these 2 conditions is.Assuming that transistor TR1 is in cut-off position (OFF) and TR2 is in saturation condition (ON) then C2 will charge charging through R2 to ground through emitter collector TR2, then when the load is full TR1 transistor gets forward so that Changing to saturation (ON) this condition will force the transistor condition TR2 to cut-off (OFF) quickly so that the C2 charge will be released through the base of TR1 and at the same time C1 fill the load to full through R3 to ground through collector emitter TR1. Then when C1 starts to empty and C2 starts full TR2 gets forward bias because C2 does not fill again, this condition make TR2 transistor change to saturation (ON) and force TR1 to turn into cut-off (OFF) and C2 load again, C1 Empty the load again until C2 is full and make TR1 become ON and TR2 becomes OFF again and so it will run like that.The condition of two states on both transistors is always cut off and saturation in turn provides the output of a continuous pulse with a frequency determined by the speed of charging and discharging time of the feedback capacitor of both parts. This fraction of the pulse generated by the flip-flop 2 transistor circuit (astable multivibrator ) Above are:

$F=\frac{1}{T}=\frac{1}{1,38 R C}$

With T is t1 + t2 as follows: $t_{1}=0,69 C_{1}R_{3}$

$t_{2}=0,69 C_{2}R_{2}$

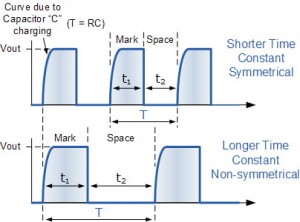
Where C1 = C2 and R2 = R3The resulting pulse frequency consists of T1 and T2 which are in opposite conditions as shown in the form of output pulses generated by the flip-flop 2 transistor circuit (free running multivibrator or astable multivibrator). The output pulse form in the symmetrical RC configuration configuration (same) and the different RC value configurations for the flip-flop circuit can be seen in the following figure.Forms Pulse Output Flip-Flop 2 Transistor Circuit (Astable Multifibrator)Output Pulse Output Flip-Flop 2 Transistor (Astable Multifibrator), flip-flop output pulse, flip flop output frequency, flip-flop output pulse, multivibratos astable output pulse, free running multivibrator output form, astable multivibrator working frequency, working frequency Free running multivibrator

Bentuk Pulsa Output Rangkaian Flip-Flop 2 Transistor (Astable Multifibrator),pulsa output flip-flop,frekuensi output flip flop,bentuk pulsa output flip-flop,pulsa output multivibratos astabil,bentuk output free running multivibrator,frekuensi kerja multivibrator astabil,frekuensi kerja free running multivibrator

                                                              X . I
                                                        FEED BACK

In everyday life, people are always dealing with electronic devices, almost everywhere must be found electronics equipment. The electronics equipment is composed of various electronic components. These components form a unity of relations called a series of electronics. This series of electronics raises an activity that helps or is very beneficial to humans. In an electronic circuit, the legs of one component with the other legs are not directly connected, but the component legs are attached or soldered to a plate or board called a PCB (Printed Circuit Board).

There are two ways of making the circuit, first conventionally and secondly computerized. Conventional circuit creation, which is to assemble the circuit itself by a board called PCB (Printed Circuit Board), which is equipped with logic gates, then checked using LED. But making the circuit itself will cost a lot, the difficulty in buying circuit equipment, and there can be a connection error or a tool used to be damaged.In modern times as it is today, many ornamental or writing lamps run using LED lights. In the flip-flop lights the compilers make is still a simple circuit, exploring this simple circuit would be a better circuit, for example in a series of running articles that are common to offices.

Formulation of the problem

Based on the description of the background, it can be formulated as follows:
1. What is the understanding of physics and electronics?
2. How to design the electronics circuit LightsFlip Flop?
3.Contents the electronics components LightsFlip Flop and its function?
4. Physical concept used in electronics circuit Flip Flop Lamp?

Basic theoryPhysics is a branch of Natural Sciences (IPA) that studies natural phenomena or natural phenomena as well as all the interactions that accompany it. The purpose of studying the gelaja is to obtain a characteristic physics product that can explain the natural phenomenon. The product of physics consists of concepts, laws, and theories. Physics has many branches including Quantum Mechanics, Fluid Mechanics, Electronics, Electronic Engineering, Electrostatics, Electrodynamics, Bioelectromagnetics, Thermodynamics, Core Physics, Physics of Waves, Optical Physics (Geometry), Cosmography orAstronomy, and Geophysics.Electronics is a science that studies the control of weak electrical currents that can be operated by controlling the flow of electrons, this electron control occurs in a vacuum or space containing low pressure gas such as gas cylinders and semiconductor materials.Flip Flop Flip circuit is a given circuit loaded LED on each side of the transition changes the output signal. The Flip Flop LED circuit with this LED is quite simple, the LED as an indicator of the signal change will alternate in turn with the on and off time equal to the charging and discharging process of the capacitor.Tools and materialsThe tools and materials we use in making Flip Flop Lamp Series are:Tool1.Solder2.Tang3. Cut out4.Multitestermaterial1.Resistor (10 KOhm)2. Capacitor (330 μF / 16 V)3.Transistor (BC 546)4.LED (5mm DIP Focus, 3 - 3.5 V, 20 Ma)5.Printed Circuit Board (PCB)6. Cable7.Timah8.The Battery

Flip Flop Flow Generation Step1. Install each component that has been prepared to the PCB in accordance with the design that has been made.2.Selanjutnya Solder each leg component and do not until there konslet or not soldering.3.Connect Battery to the circuit.4.If successful then the LED light will be rotated alternately.5.Flip Flop circuit pack as planned by the group.How Flip Flop Lights Work1.The electric current flows to fill 2 capacitors2. The fully charged capacitor will first unload the load first.3. Capacitor 1 discharges its charge to the base of the transistor 1. If the charge discharged capacitor 1 corresponds to the required base in activating the transistor 1. Then the transistor 1 is on, so the current is allowed to pass through the collector to the emitter.4.Akibatnya LED the right side associated with this 1st transistor will light up.5. While the capacitor 2 is off, because the charge in capacitor 2 can not be removed. So the left side is not on. Although there is a charge flowing from the collector to the transistor emitter 2, it is still not enough to make the led 2 turn on.6. When the capacitor 1 runs out of charge, the capacitor 2 automatically discharges the charge, thus activating the transistor 2, and the led left turns on. While the 1st capacitor still charges the charge, so the transistor 1 off, causing the right led also off.

Electronic Components Used and their Functions1.Resistor (obstacle)The general shape of this component is rounded elongated and has bracelets of value. The function of the resistor is to inhibit the electric current flowing in an electronic circuit. This component is very easy to find in all electronic circuits such as Television, Radio, Tape Amplifier and so on.2.KapasitorDefinition A capacitor is an electronic component device that serves to store an electrical charge and consists of two conductors separated by an insulating material (dielectric) on each conductor or so-called chip. The capacitor is usually referred to as a condenser which is an electrical component made in such a way that it is capable of storing an electrical charge.3.TransistorTransistors are semi conductor components that have 3 foot electrodes, namely Base (B), Colector (C) and Emitter (E). With the 3 feet of the electrode, the voltage or current flowing on one leg will regulate the larger current for the other 2 terminals. Transistor functions include: As a breaker and switching, As a voltage stabilizer, Flow, Strengthen the current in the circuit.4.Light Emitting Diode (LED)Light Emitting Diodes or often abbreviated with LEDs are electronics components that can emit monochromatic light when given forward voltage. LED is a family of Diodes made of semiconductor materials. LED technology has many advantages such as non-heat, long lasting, no harmful ingredients such as mercury, and low power and small form. LED Functions include: Home Lighting Light, Street Lighting Light, LCD Backlight (TV, Mobile Display, Monitor), Indicator Light, Infrared Transmitter on Remote Control (TV, AC, AV Player).5. BatteryA battery is a chemical-electrical device that stores energy and exerts its energy in the form of electricity. In a circuit, the battery acts as a voltage source.6.Printed Circuit Board (PCB)Printed Circuit Board or commonly abbreviated PCB is a board that is used to support all the components of electronics that are above it, PCB board also has conductor lines made of copper and serves to connect between one component with other components.

Concepts or Principles of Physics UsedThe principle used in the flip flop circuit is the charging and discharging of the capacitor. Capacitors are electronic components that can store electrical charges so that the applications are widely used to make oscillations, timers, and voltage stabilizers in power supply circuits. The capacitor can store the electrical charge according to the capacitance capacity.ConclusionAfter discussing in detail, analyze and see the function of the series on the previous pages, it can be concluded as follows. By studying digital control system we can know how to make a Flip Flop Flop circuit and can develop the science to make tools useful for people's lives.Flip Flop is a multivibrator family that has stable stable or called Bistobil Multivibrator. The basic principle of the Flip Flop is a basic electronic component such as transistors, resistors, and diodes that are assembled into a series of electronics that can work according to the design in the arrangement

X . II
MEMORY PROCESSOR

Hasil gambar untuk akumulator memori elektronika

Parallel Processor

Parallel Processor
Parallel Processor is a processor where the implementation of the instructions simultaneously.
So as to cause the execution of an event:
1. Dlam same time interval
2. In the same time

1. Interconnection Network
There are 5 components
1. CPU
2. Memory
3. Interface: equipment that brings in and out messages from CPU and Memory
4. Connector: the physical channel through which the bits go
5. Switch: equipment that has many portinput and output ports
Communication between different terminals should be possible with a particular medium. Effective interconnection between processors and modules is important in computer environments. Using a ribbon-themed architecture is a practical solution since bus is only a good choice when used to connect components with small amounts. The number of components in an IC module increases over time. Therefore, the bus topology is not a topology suitable for interconnection needs of components in IC modules. It also can not be scaled, tested, and less customizable, and results in a small fault tolerance performance. On the other hand, a crossbar provides full interconnection between all terminals of a system but is considered very complex, expensive to make, and difficult to control. For this reason the interconnection network is a good communication media solution for computer and telecommunication systems. This network limits the pathways between different communication terminals to reduce the complexity of constructing switching elements.2. SIMD Machine & MMID Machine

SIMD Machine
SIMD stands for "Single Instruction, Multiple Data", is about a term in computing that will refer to a set of operations used to handle large amounts of data in parallel efficiently, as happens in a vector processor or an array processor. SIMD was first popularized on a large-scale super computer, although it has now been found on personal computers. Examples of applications that can take advantage of SIMD are applications that have the same value added to multiple data points (data points), which are common in multimedia applications. One example of its operation is to change the brightness of an image. Each of a 24-bit image contains three 8-bit brightness values of red, green (green), and blue (blue) portions. To change the brightness, the values R, G, and B will be read from memory, and a new value is added (or subtracted) to those R, G, B values and the final value will be returned (rewritten) to memory.The processor that has SIMD offers two advantages, namely:
Direct data can be understood in the form of data blocks, compared to some separate data individually. By using a data block, the processor can load the data as a whole at the same time. Instead of doing some instructions "grab this pixel, then take the pixel, dst", a SIMD processor will do it in an instruction only "grab all those pixels!" (The term "all" is a value different from one design to another ). Obviously, this can reduce much processing time (due to instructions issued only one for a set of data), when compared to traditional processor designs that do not have a SIMD (which gives one instruction for one data only). SIMD systems generally only include instructions that can be applied to all data in one operation. In other words, the SIMD system can work by loading multiple data points simultaneously, and perform operations on the data points simultaneously.

MMID machine
MIMD is an abbreviation of "Multiple Instruction Stream-Multiple Data Stream" which is a computer that has several autonomous processors capable of performing different instructions on different data. Distributed systems are commonly known as MIMDs, either using a shared memory space or a distributed memory space. On a pure MIMD computer system there is an interaction between processing. This is because the entire flow to and from memory comes from the same data space for all the processors. The MIMD computer is tightly coupled if the level of interaction between high processing and loosely coupled is called if the interaction rate between the processors is low.

3. Replacement Architecture
In the field of computer engineering, replacement architecture is the concept of planning or basic operating structure in the computer or it can be said the blueprint plan of the functional description of the needs of the hardware designed, the implementation of the planning of each section such as CPU, RAM, ROM, Memory Cache, etc.

X . III
Flip flop development over time to computer memory

The US Army's ENIAC project was the first computer to have memory storage capacity in any form. Assembled in the Fall of 1945, ENIAC was the pinnacle of modern technology (well, at least at the time). It was a 30 ton monster, with thiry seperate units, plus power supply and forced-air cooling. 19,000 vaccum tubes, 1,500 relays, and hundreds of thousands of resistors, capacitors, and inductors consuming almost 200 kilowatts of electrical power, ENIAC was a glorified calculator, capable of addition, subtraction, multiplication, division, sign differentiation, and square root extraction.

Despite it's unfavorable comparison to modern computers, ENIAC was state-of-the-art for in it's time. ENIAC was the world's first electronic digital computer, and many of it's features are still used in computers today. The standard circuitry concepts of gates (logical "and"), buffers (logical "or"), and the use of flip-flops as storage and control devices first appeared in the ENIAC.

ENIAC had no central memory, per se. Rather, it had a series of twenty accumulators, which functioned as computational and storage devices. Each accumulator could store one signed 10-digit decimal number. The accumulator functioned as follows:

The basic unit of memory was a flip-flop. Each flip-flop circuit contained two triodes, designed so that only one triode could conduct at any given time. Each circuit had two inputs and two outputs. In the set, or normal position, one of the outputs was positive, the other was negative. In the reset, or abnormal position, the poles were reversed.
Ten flip-flops interconnected by count digit pulses, formed a decade ring counter. Each ring counter is capable of storing and adding numbers. The ring counters had the following characteristics:
1. At any one time, only one flip-flop in the ring could be in the reset state.
2. A pulse to the counter input reset the initial flip-flop in the chain.
3. The circuit could be cleared so that a specific flip-flop was in the reset position while the others remained set.
Each flip-flop in the ring was concidered a stage, and the reception of a pulse on the input side advanced the counter by one stage.
A variation on the counter circuit, the PM counter, acted as the sign bit for the number.
One PM counter and 10 ring counters, one ring for each decimal place, made up an accumulator.

ENIAC operated under the control of a series of pulses from a cycling unit, which emitted pulses at 10 microsecond intervals.

ENIAC led the computer field through 1952. In 1953, ENIAC's memory capacity was increased with the addition of a 100-word static magnetic-memory core. Built by the Burroughs Corporation, using binary coded decimal number system, the memory core was the first ever of it's kind. The core was operational three days after installation, and run until ENIAC was retired.....quite a feat, given the breakdown-prone ENIAC.

ENIAC: 30 tons of fury

Core Dump

After it's creation in 1952, core memory remained the fastest form of memory available until the late 1980's. Core memory (also known as main memory), is composed of a series of donut-shaped magnets, called cores. The cores were treated as binary switches. Each core could be polarized in either a clockwise or counterclockwise fashion, thus altering the positive or negative charge of the "donut" changed it's state.

Until fairly recently, core was the prominent form of memory for computing (by 1976, 95% of the worlds computers used core memories). It had several features that made it attractive for computer hardware designers. First, it was cheap. Dirt cheap. In 1960, when computers were beginning to be widely used in large commercial enterprises, core memory cost about 20 cents a bit. By 1974, with the wide-spread use of semi-conductors in computers, core memory was running slightly less than a penny per bit. Secondly, since core memory relied on changing the polarity of ferrite magnets for retaining information, core would never lose the information it contained. A loss of power would not effect the memory, since the states of the magnets wouldn't be changed. In a similar vein, radiation from the machine would have no effect on the state of the memory.

Core memory is organized in 2-dimensional matrices, usually in planes of 64X64 or 128X128. These planes of memory (called "mats") were then stacked to form memory banks, with each individual core barely visible to the human eye.. The core read/write wires were split into two wires (column, row), each wire carrying half of the necessary threshold switching current. This allowed for the addressing of specific memory cores in the matrix for reading and writing.

Currently, molecular memory is being

A 1951 core memory design. Each core show here is several millimeters in diameter.

It's Glorious Future

With the rapid changes in computing technology that occur almost daily, it shouldn't be suprising that new paradigms of RAM are being researched. Below are some examples of where the future of RAM technology may be heading.....

Holographic Memory

We are all familiar with holograms; those cool little optical tricks that create 3D images that seem to follow you around the room. You can get them for a buck at the Dollar Store. But I bet you didn't realize that holograms have the potential to store immense quantities of data in a very compact space. While it's still a few years away from being a commercial product, holographic memory modules have the potential to put gigabytes of memory capacity on your motherboard. Now, I'm not going to jive you: I don't understand this stuff on a very technical level. It's still pretty theoretical. But I'll explain what I do know, and hopefully you'll be able to grasp just how this exciting old technology can be used as a computing medium.

First, what is a hologram? Well, when two coherent beams of light (such as laser beams) intersect in a holographic medium (such as liquid crystal), they leave an interference pattern in the medium at the point of intersection. This interference pattern is what we call a hologram. It has the property that if one of the beams of light is shown through the pattern, it appears as though the second source of light is also illuminating the pattern, making the pattern "jump out at you".

Now, instead of having an image projected, imagine that the source was a page of data. By having a source illuminate a pattern created with the data page, the page of data "comes out". Imagine futher that a series of patterns had been grated into the medium, each with a different page of data. With one laser beam, you could read the data off the holographic crystal. And by simply rotating the crystal a fraction of a degree, the laser would be intersecting a different interference pattern, which would access a whole new page of data! Instead of accessing a series of bits, you would be accessing megabytes of data at a time!

Pretty neat, huh?

The implications are pretty obvious. A tremendous amount of data could be stored on a tiny chip. The only limitations would be in the size of the reading and writing optical systems. While this technology is not ready for widespread use, it is exciting to think that computers are approaching this level of capability at.....well, at the speed of light.

Here is an example of a holographic memory system. Obviously not ready for PC use.

Molecular Memory

Here is a form of memory under research that is very theoretical. Conventional wisdom says that although current production methods can cram large amounts of data into the small space of a chip, eventually there will reach a point where we can't cram anymore on there. So, what do we do? According to researchers, we look for something smaller to write on; say, about the size of a molecule, or even an atom.

Current research is focused on bacteriorhodopsin, a protein found in the membrane of a microorganism called halobacterium halobium, which thrives in salt-water marshes. The organism uses these proteins for photosynthesis when oxygen levels in the environment are too low for it to use respiration for energy. The protein also has a feature that attracts it to researchers: under certain light conditions, the protein changes it's physical structure.

The protein is remarkably stable, capable of holding a give state for years at a time (researchers have molecular memory modules which have held their data for two years, and it is theorized that they could remain stable for up to five years). The basis of this memory technology is that in it's different physical strucutres, the bacteriorhodopsin protein will absorb different light spectra. A laser of a certain color is used to flip the proteins from one state to the other. To read the data (and this is the slick part), a red laser is show upon a page of data, with a photosensitive receptor behind the memory module. Protein in the O state (binary 0) will absorb the red light, while protein in the Q state (binary 1) will let the beam pass through onto the photoreceptor, which reads the binary information.

Current molecular memory design is a 1" X 1" X 2" transparent curvette. The proteins are held inside the curvette by a polymerized gel. Theoretically, this dinky chip can contain upwards of a terabyte of data (roughly one million megabytes). In practice, researchers have only managed to store 800 megs of data. Still, this is an impressive accomplishment, and the designers have realistic expectations to to have this chip hold 1.7 gigs of data within the next few years. And while the reading is somewhat slow (comparable to some slower forms of todays memory), it returns over a meg of data per read.

Hasil gambar untuk computer memory accumulator on flip flop

X . IIII

FLIP FLOP and REGISTER

Flip-Flops and Registers

Consider the following circuit:

Here are two NAND gates with their outputs cross-connected to one input on each. This arrangement makes use of feedback. When R and S are 1, the circuit has two stable states: Q can be 1 and Q' 0, or Q can be 0 and Q' 1. Suppose the circuit has Q = 1. If S goes to 0, even momentarily, the circuit will flip states and Q will become 0. If S goes back to 1, Q will remain 0 (and Q' 1). The circuit "remembers" that S was 0 at some time in the past. Then, if R goes to 0, the circuit will flip back to the way it was initially, with Q = 1 and Q' = 0. This behavior is central to circuits that hold data. These circuits are used in computer memory and registers. The circuit above is called the R-S (reset-set) latch. It is the central circuit of the more complex circuits called flip-flops.
Here is a circuit called a data or D-type flip-flop:

It is an RS latch with additonal NAND gates that make it simple to control. When Enable is 0, both control NAND gates will have a 1 output, and the RS latch will remain stable. When Enable = 1, Q will become equal to Data. If Data changes while Enable = 1, Q will also change. When Enable goes back to 0, the most recent value of D will remain on the Q output (and Q' will be the opposite). The D-type flip-flop has its own symbol, of course.

This flip-flop is sometimes called a transparent latch, because while Enable is high, the data outputs follow the data input. Because the latch holds the data forever while the enable input is low, it can be used to store information, for example, in a computer memory. Lots of latches plus a big decoder equals one computer memory.
If two data-type latches are connected as below, the result is an edge-triggered latch:

In this configuration, two transparent D-type latches are connected in tandem. The enable input, when low, causes the first flip-flop to be in the transparent state, and the second flip-flop to be locked. When Enable goes high, the second flip flop becomes transparent first, then after a brief delay the first flip-flop becomes locked. The output of the second flip-flop will show the locked output of the first. Even though the second latch is in its transparent state, the data on the output will not change, because the first latch is locked. When enable goes low again, the second flip-flop becomes locked first, then the first becomes transparent. The data output will remain unchanging, because now the second flip-flop is locked. The only time new data can be stored in the circuit, is during the brief moment when the enable input goes from low to high. This transition is referred to as a rising clock edge, and so this tandem latch configuration is called a rising edge triggered latch. The two flip-flops and inverter can be enclosed by a box, and represented by a single symbol. The Enable input of the transparent latch is replaced by the clock pulse (CP) input. The edge-triggered latch is one of the central circuits in computer design.

It allows the following:

Assume a series of pulses (voltage going from 0 to 5V) is coming in to the CP input. The Q output will be switching values every other clock pulse. This divides the clock frequency by two. A chain of these acts as a binary counter.
The most important use of the edge triggered flip-flop is in the data register. The characteristic of loading data only at the rising edge of the clock pulse is critical in creating the computer machine cycle, as we will see. A register is simply a collection of edge triggered flip-flops. Here is a four-bit register:

The edge-triggered flip-flop register is crucial for the computer machine cycle. The machine cycle can be characterized by the following (very much abbreviated) diagram.

The computer clock provides a continuous stream of pulses to the computer processor. With each upward swing of the voltage on the clock output, the register loads whatever values are present on its inputs. As soon as the data is loaded it appears on the outputs, and stays there steady throughout the rest of the clock cycle. The data on the register outputs is used as input for the computer circuits that carry out the operations desired. For example, the accumulator register data output may be directed by a multiplexor to one of the inputs of the ALU, where it serves as an addend. The result of the addition appears on the ALU outputs, which can be directed by multiplexors to the inputs of the same accumulator register. The result waits at the inputs of the register for the next upward swing of voltage on the CP register input, sometimes called the write input (WR). When this occurs, the ALU result is loaded into the register and displayed on the outputs. The value held in the register from the previous cycle is overwritten and discarded, having served its purpose. The cycle is repeated endlessly, the data following paths dictated the program instructions, which control the various multiplexors and registers. If the accumulator had used transparent latches, the ALU result would feed through the register, to the ALU, back to the register and through again to the computer circuits in an uncontrolled loop. The edge-triggered register ensures that the result is written in an instant, and then the inputs close, allowing the computer to perform its operations in an orderly and stable way.

Design and Construction

The completed computer is shown below. The central three boards (ALU, main board and control) make up what is commonly thought of as a computer processor, or central processing unit (CPU). The processor takes instructions and data from the memory-input/output, processes them, and puts data back into the memory-input/output.

Each board is a separate functional unit. The four outside boards (ALU, display, control and memory) could be tested thoroughly using a simple test board before being connected to the central main board.
Before I built this computer, I had to design it. My priority was simplicity. I did not want a processor that was fast, or complex. I wanted it to work. This processor that I designed and built is an accumulator-memory machine, that is, a single register is used in programming. I wanted an instruction set similar to those of the 8-bit microprocessors I was used to. However, the Z-80 and 6502 CPUs had complex instruction sets, with variable instruction lengths. I knew from experience that a programmer uses only a subset of these, so I designed an instruction set that was similar to this commonly-used subset. It has 16 instructions in all, with eight arithmetic-logical operations, and eight data movement and jump instructions. In retrospect, it is probably too heavy on the arithmetic-logical instructions, but I wanted to design and build a full ALU. Here is the instruction set.

Hex Opcode	Instruction Mnemonic	Operation Performed
0	ADD	Adds contents of memory to accumulator
1	ADC	Adds contents of memory and carry to accumulator
2	SUB	Subtracts contents of memory from accumulator
3	SBC	Subtracts contents of memory and complemented carry from accumulator
4	AND	Binary AND of memory with accumulator
5	OR	Binary OR of memory with accumulator
6	XOR	Binary XOR of memory with accumulator
7	NOT	Complements accumulator (operand ignored)
8	LDI	Loads 12-bit value of operand into accumulator (immediate load)
9	LDM	Loads contents of memory into accumulator
A	STM	Stores contents of accumulator to memory
B	JMP	Jumps to memory location
C	JPI	Jumps to contents of memory location (indirect jump)
D	JPZ	If accumulator = zero, jumps to memory location
E	JPM	If accumulator is negative (minus), jumps to memory location
F	JPC	If carry flag is set, jumps to memory location

I chose a 16-bit instruction word width. With 16 instructions, this means a 4-bit operation code, and a 12-bit operand:

The operand is usually a memory address, so this gives the processor a 12-bit (4 kiloword) address space. I built the memory 16 bits wide so an instruction could be loaded in one piece. In my original design, I planned to have the entire program in 2K of ROM, with 1K of RAM for data storage, and 1K of address space set aside for input and output. The accumulator would be 12 bits wide, and the ALU (arithmetic-logic unit) also 12 bits wide. This was the size of the operand of the immediate load instruction, and was big enough to prove that the computer worked. Later, after I had the processor working, I wanted to load programs into RAM from input. I added 4 bits to the accumulator to allow this (details in main and programming).
After I had decided on the basic architecture of the processor, I drew a detailed plan of the computer that shows all the elements through which the data would move. Here is a diagram of my computer, done in the style of the diagrams developed in the textbook Computer Organization and Design:

The elements contained in the computer are listed below:

Memory, 16 bits wide, 4K words long
ALU, 12 bits wide
Multiplexors:

Program counter source, 12 bits, 3 inputs
Address source, 12 bits, 2 inputs
Accumulator source, 12 bits, 3 inputs
ALU source A, 12 bits, 2 inputs
ALU source B, 12 bits, 2 inputs
ALU operation source, 4 bits, 2 inputs

Registers:

Program counter, 12 bits
Instruction register, 16 bits
Accumulator, 12 bits
Data register, 12 bits
Carry flip-flop, 1 bit

Data Bus Buffer, 12 bits

Once the data path had been defined, I could design the control logic. The control logic of the computer is the real heart of the machine. It selects the multiplexor inputs and decides which registers will be written every clock cycle, based on the operation being performed.
Another consideration was the clock speed. The 74LS series gates have about a 10 nanosecond (ns) delay time, and I would probably not have more than 30 gates in any of my logic chains. The slowest part of the machine would be the memory. I used an EPROM with a 250 ns delay. It seemed that a 500 ns cycle time would be enough, but to be safe I started with a 1000 ns cycle (= 1 megahertz clock frequency). After I knew the computer was working, I ran it at 2 MHz, and it worked fine.
The computer was constructed of 74LS series chips in wire-wrap sockets. (Note: the sockets cost more than the I.C.s!) The connections were made by wire-wrapping, with my trusty hand tool. After wrapping, the connections were checked with a magnifying glass. I only used solder on the power connections, but I probably didn't need to. I tested the outside boards with my test board. I also used a logic probe to debug circuits that weren't working properly.
Once construction was complete I tested it with some simple programs . Once I was sure it was working I added a serial port to the memory-input/output board and wrote a short "operating system". This program allows the user to enter a program as a series of hexadecimal numbers from a terminal. I used both a dumb terminal ($5 at a local flea market) or an old 486 computer running a terminal program. The 486 allows the user to store each program as a text file, and just load it into the computer using a text transfer.

Arithmetic/Logic Unit (ALU)

The Arithmetic-Logic Unit (ALU) described here is part of my homebuilt computer processor (CPU). It performs the computer processor computations. These are the arithmetic operations (addition and subtraction) and the logical operations (AND, OR, XOR and NOT) that are done during execution of the corresponding machine instructions. The ALU also performs the program counter incrementation during the instruction fetch.
I built the ALU from simple logic circuits. I used AND, OR, XOR and NOT gates, and four-bit adders. Subtraction is performed by two's-complement addition, that is, by inverting and adding one to the subtraend.
The lower three bits of the instruction opcodes are used as ALU opcodes. A small AND-OR array provides the logic needed to interpret these opcodes. You may realize that the ALU will perform computations during the non-arithmetic instructions, like the jumps and memory loads. However, with these instructions, the control logic of the processor makes sure that the result is ignored (not written to the accumulator). Here is a diagram of the ALU design, for one bit. The carrys are rippled to the subsequent adders.

The ALU performs the four logical operations and addition continually on every pair of operands. However, only the result selected by the output multiplexor (as determined by the ALU logic) will appear on the ALU output. The processor control logic determines if the carry result will be stored in the carry flip-flop on the main board.
The ALU logic circuit is here. I used a one-of-eight decoder for the AND plane.

There is a flaw in the ALU design, it does not perform subtract with borrow correctly. It will add the complemented carry (one bit), but to work properly it should add the two's complement of the carry. The two's complement of the carry would be a 12-bit value, and to perform properly the ALU would need an additional 12-bit adder to do this. However, one could still do subtract with borrow using software, by doing subtract, then subtracting one from the result if there was a borrow on the previous subtraction.

Register Display

Not much to say about this. It is simply LED's with built-in current limiting resistors, connected by way of buffers to the register outputs. It is not needed for proper operation of the computer, but it is critical in the troubleshooting phase. The display is also pleasing to watch when the computer is running. With a slow clock, it is easy to follow what the computer is doing.

Control Logic

The control logic is a finite state machine. A finite state machine is both a theoretical and actual device that uses sequential logic to perform a series of steps. The finite state machine has, like other logic circuits, an input and an output. In addition, it has a state, which is a number stored inside it. For computer control, the input is the current instruction and the current conditions (zero, minus or carry). The output is the bit pattern that controls the main board register write inputs and the main board multiplexors, which cause the instruction to be carried out. In addition to the control output, there is a next-state output that is fed back to the input of the finite state machine. At the clock edge, the next-state becomes the current state. The finite state machine used in my computer is a Moore machine, in which the outputs depend only on the current state. The next state, however, is determined by both the inputs and the current state.
There are 11 states defined in the control logic for this computer processor. The finite state machine logic is made of a 4-bit state register and an AND-OR array. There are no large-scale integrated circuits used. The large chip at the lower left is a 4 to 16 decoder. The current state is displayed on the four LEDs near the top of the board. The states are defined as follows:

State	Action Performed	Operations that use the state
0	Instruction fetch/Program counter increment	All
1	Instruction interpretation	All
2	Data fetch	Arithmetic/logical operations
3	Arithmetic instruction, includes carry write	ADD, SUB, ADC, SBC
4	Logic instruction, no carry write	AND, OR, XOR, NOT
5	Load accumulator immediate (value in current instruction)	LDI
6	Load accumulator from memory	LDM
7	Store accumulator to memory, first step	STM
8	Store accumulator to memory, second step	STM
9	Jump immediate (target address in current instruction)	JMP, and conditional jumps when condition true
10	Jump indirect (target address in memory)	JPI

Instructions are carried out by cycling through a series of states in the correct order. For example, the ADD instruction in carried out by running through states 0, 1, 2 and 3. Here are the states for each instruction:

Hex Opcode	Instruction Mnemonic	States
0	ADD	0, 1, 2, 3
1	ADC	0, 1, 2, 3
2	SUB	0, 1, 2, 3
3	SBC	0, 1, 2, 3
4	AND	0, 1, 2, 4
5	OR	0, 1, 2, 4
6	XOR	0, 1, 2, 4
7	NOT	0, 1, 4
8	LDI	0, 1, 5
9	LDM	0, 1, 6
A	STM	0, 1, 7, 8
B	JMP	0, 1, 9
C	JPI	0, 1, 10
D	JPZ, condition met	0, 1, 9
D	JPZ, condition not met	0, 1
E	JPM, condition met	0, 1, 9
E	JPM, condition not met	0, 1
F	JPC, condition met	0, 1, 9
F	JPC, condition not met	0, 1

The correct arithmetic/logical operation is performed by the ALU, because it reads the lower 3 bits of the opcode directly. At the end of each series of states, the next state is 0, causing a new instruction to be fetched. Each state takes exactly one clock cycle, so the longest instructions are 4 clock cycles long. Thus, at a clock speed of 1 MHz, the computer can perform 250,000 arithmetic instructions per second. The control logic was thoroughly tested after construction using the test board.
The control board also has the reset and clock circuits. Reset is performed by forcing the program counter and state registers to zero. When the reset is released, the computer will fetch the instruction in memory location 000h and start from there. There are three clocks. The crystal is the fast clock; a 1.8 MHz clock is currently in place. A slow 2 Hz clock (2 cycles per second) is made from an R-C oscillator. This slow clock allows debugging of the computer hardware. A single-step clock is also present. The wire protruding from under the lower edge of the board is used to ground two contacts seen nearby, causing a flip-flop to change states. An LED shows the state of the clock line. The DIP switches select the clock being used.

Memory and Input/Output

This board is the only one in the computer that has large-scale integrated circuits (LSI). The LSI's are the EPROMs, RAM, and a UART for serial communication. Other chips are 74LS series buffers and address decoders. The rows of switches and the nearby rows of LED's are simple 16-bit input and output ports, respectively. These are very useful for debugging of hardware and software. There is also a 16-bit port configured as a byte-switcher. That is, when a 16-bit word is written to the port, then read from the port, it comes out with its low- and high-order bytes switched. This port allows one to download the high-order bytes from the 16-bit memory to the 8-bit serial port. The computer cannot accomplish this by arithmetic because the path through the ALU is only 12-bits wide.

Main Board (Data Path)

This board contains the multiplexors and data registers shown in the main computer diagram seen below, and described more completely in design. The memory and the ALU are on separate boards.

As mentioned in Design I added 4 bits to the accumulator in order to move full instruction words between input and memory, or ROM and RAM. The additional upper 4 bits of the accumulator come directly from the memory, bypassing the accumulator source multiplexor (not shown in the diagram). Whenever the accumulator is written (in arithmetic-logical instructions and accumulator loads), the upper 4 bits will therefore be from the most recently accessed memory location. Only the 12 low-order bits of the accumulator output are passed to ALU source multiplexor A. The full 16 bits of the accumulator are passed to the memory, however. Similarly, the low-order 12 bits of memory data are passed to the Data register, the PC source multiplexor input 2, and the accumulator multiplexor input 2, but the full 16 bits are passed to the instruction register (I.R.). The upper 4 bits of the I.R. are passed to the ALU operation source multiplexor, and the lower 12 bits to the accumulator source multiplexor input 1.
Some sharp visitors have noticed that the Data register does not appear to be necessary. They are correct. I was concerned that the cycle-time might not allow for data from the memory to pass through the ALU adders in time, since the adders are slowed up by having the carries "ripple" though. However, at a clock speed of 1 MHz, there is enough time for this, and I could have eliminated the Data register fetch state. But, if I try to run the computer at 4 MHz, the Data register, and its accompanying fetch state, would be necessary. I have never tried to run it that fast, though.
Also on this board, but not diagrammed, is the logic for the zero condition calculation, which is just a 16-bit NOR of the the accumulator bits. Another feature is a memory write circuit. Since the RAM is written by the level of the memory write control line, and not the edge, I used a flip-flop and an inverted system clock to create the proper timing. There are two memory write states used as seen in Control. The two states and the memory write circuit make sure that the data is held long enough, and that the memory write signal is dropped before the data changes.
One final "extra" was needed. It is imperative that all the registers are written at the same time by a clock edge in order for the computer to work. However, the logic circuits that determine if a register is to be written produce only a logic level, and they finish at different times because there are varying numbers of gates in the logic paths. The solution was to have a single register collect the write signals, and then at the same time on the same clock edge send them to their respective register write inputs. The register write inputs would see an upgoing clock edge if the logic had produced a 1, and no edge if it had produced a 0. An time-offset clock signal then resets the register after a short delay, and all the signals return to zero. This is important because if a register is to be written on two consecutive cycles, the register write signal must go back to zero in order for the next signal to produce an edge. I used a chain of several inverters to create the delay.
This board could not be tested apart from the Control, Memory and ALU boards, but since these other boards could be tested thoroughly, the debugging of the main board was pretty simple. In fact, I think it worked the first time I tried it.

Programming and Operation

The computer has a simple architecture. It has only one programmer-accessible register, the accumulator. Originally 12 bits wide, I added another 4 bits later to allow memory transfers. All load and store operations move data between memory and the accumulator, and the arithmetic-logical instructions use the accumulator as one operand, and data fetched from memory as the other. (The NOT operation, of course, only operates on the accumulator, and the operand in the instruction is ignored.) The results of arithmetic-logical operations are stored in the accumulator. Only the original 12 lower bits of the accumulator can be used for arithmetic-logical operations.
The computer has an instruction word size of 16 bits. The four leftmost bits of an instruction word are the operation code, and the 12 rightmost bits are the operand, like this:

In almost all cases, the operand is a memory address. In the case of the arithmetic-logical instructions the memory address holds the data that is to be operated on together with the data in the accumulator. For the load and store operations, the address is the source or target of the data to be moved. The one exception is the immediate load, LDI. In this case, the 12-bit operand value itself is placed in the accumulator. The various jump instructions use the operand as the target address, except the indirect jump JPI, in which the target address is held in the memory location pointed to by the operand. Here is the instruction set:

Hex Opcode	Instruction Mnemonic	Operation Performed
0	ADD	Adds contents of memory to accumulator
1	ADC	Adds contents of memory and carry to accumulator
2	SUB	Subtracts contents of memory from accumulator
3	SBC	Subtracts contents of memory and complemented carry from accumulator
4	AND	Binary AND of memory with accumulator
5	OR	Binary OR of memory with accumulator
6	XOR	Binary XOR of memory with accumulator
7	NOT	Complements accumulator (operand ignored)
8	LDI	Loads 12-bit value of operand into accumulator (immediate load)
9	LDM	Loads contents of memory into accumulator
A	STM	Stores contents of accumulator to memory
B	JMP	Jumps to memory location
C	JPI	Jumps to contents of memory location (indirect jump)
D	JPZ	If accumulator = zero, jumps to memory location
E	JPM	If accumulator is negative (minus), jumps to memory location
F	JPC	If carry flag is set, jumps to memory location

The address space of the computer matches the size of the instruction word operand, 12 bits or 4 kilowords. The memory and input/output ports are addressed in the same way--there are no special input or output instructions. The address space in the computer is laid out this way:

000h to 7FFh (2048 words) Programmable, read-only memory (ROM)

800h to BFFh (1024 words) Static random-access memory (RAM)

C00h to FFFh (1024 ports) Input/output (I/O)

There are 5 input and 5 output ports in the computer, on the memory input/output board. The switch inputs, LED outputs and byte switcher ports are 16 bits wide. The UART ports are eight bits wide. Only the low-order eight bits of the 16 bit accumulator are transferred in UART writes. In UART reads, the upper eight bits of the accumulator are padded with zeros. Here are the computer input and output ports:

Address	Input	Output
C00h	DIP switch bank 1	LED bank 1
C01h	DIP switch bank 2	LED bank 2
C02h	Byte switcher	Byte switcher
C03h	UART data	UART data
C04h	UART status	UART control

The very first program I ran was a simple port reflector:

Code in ROM
Label	Location (hex)	Machine Code (hex)	Mnemonic	Operand	Comment
Start	0 00	9 C 00	LDM	Port_0	Get number from switches
	0 01	A C 00	STM	Port_0	Display number on LED's
	0 02	B 0 00	JMP	Start	Do it again

When this program was running, I knew the basic structure of the computer was sound. To further test the machine I wrote the following program. This finds the largest factor of an integer, input from DIP switch bank 1. It is the same program as that first run by the first true computer, the Manchester Mark I "Baby" in 1948. Of course, my instruction set is different than the "Baby's" which had only 7 instructions!

Code in ROM
Label	Location (hex)	Machine Code (hex)	Mnemonic	Operand	Comment
Start	0 00	9 C 00	LDM	Port_0	Get number to factor from input port
	0 01	A 8 00	STM	Original_number	Store number to factor in memory
	0 02	A 8 01	STM	Factor	Starting factor = original number
Loop_1	0 03	9 8 01	LDM	Factor	Factor loop
	0 04	2 0 0F	SUB	One	New factor = old factor - 1
	0 05	D 0 0C	JPZ	Quit	If factor = 0, better quit (mistake)
	0 06	A 8 01	STM	Factor	Store new factor
	0 07	9 8 00	LDM	Original_number	Test factor by
Loop_2	0 08	2 8 01	SUB	Factor	subtracting repeatedly from original number
	0 09	D 0 0C	JPZ	Quit	Factor found-quit
	0 0A	E 0 03	JPM	Loop_1	Went past zero, not a factor
	0 0B	B 0 08	JMP	Loop_2	Still testing
Quit	0 0C	9 8 01	LDM	Factor	Get the proven factor and
	0 0D	A C 00	STM	Port_0	Display on the output
	0 0E	B 0 00	JMP	Start	Start over
One	0 0F	0 0 01	(constant)
Variables in RAM
Label	Location (hex)
Original_number	8 00
Factor	8 01

This program tests an essential subset of the instructions, including the arithmetic instructions and two of the conditional jumps. It also tests the RAM. After this, I decided to write a program loader. This program takes hexidecimal character input from a terminal, creates 16-bit instruction words, and loads these into RAM. When the Ctrl-C key is pressed, the RAM program is executed. I have used both a dumb terminal and a 486 running a terminal emulation to enter programs. The 486 allows me to save the programs as text files, and download them as a text transfer. The program loader is here if you want to see it.

Computer Operation

The final configuration of the finished computer allows the computer to receive a program by way of the serial port. The clock speed switch on the logic board is set to 1.8 MHz (position number 7 on). This results in a serial port baud rate of 9600. The input port 1 switches (lower bank) are set to B08Eh, as seen in the picture of the Memory-I/O board. When the computer is started (taken out of reset), it begins execution in ROM at location 000h. There is an instruction there that jumps to the I/O port location and executes whatever instruction it finds there. This feature was put in during the troubleshooting phase of development to allow testing of the computer using a variety of routines stored in ROM. To run a particular test, a jump to that test is put on the port 1 switches. B08Eh is JMP 08Eh. Location 08Eh is the entry point for the program loader.
The computer's serial port is connected to a dumb terminal (or PC running a terminal program) set for 9600 baud, one stop bit, no parity. Power is applied to the computer with the Reset/Run switch in the Reset position. A garbage character may appear on the terminal screen. The programmer may clear the terminal screen if the terminal has this ability. The computer is switched to Run. At this point the computer is ready to take instructions.
The program loader takes character input from the terminal and converts it to machine code instructions placed in RAM beginning at location 80Ah. Instructions are entered as four character hexadecimal numbers using upper case letters and the ten Arabic numerals. The program does not check for errors, and lower case letters or characters other than 0-9 and A-F will cause it to behave unpredictably. Each character is echoed back to the terminal, and after the full four characters of each instruction are received, a return/linefeed is sent back to the terminal. No return characters should be entered by the programmer, just the hexadecimal numerals. When all the code has been entered, the programmer enters a control-C character. This causes a jump to 80Ah, and the program begins execution.

X . IIIIIII

Ilustration flip flop on computer in game

To ultimately understand how the computer functions in-game, it is necessary to first start with an understanding of what hoiktronics is. At the heart of hoiktronics in Terraria is the idea of altering signaling pathways based on inputs, thus altering outputs. One way of accomplishing this is by having two hoik paths at right angles to one another, and the actuation state of certain blocks at the junction point dictates which path the signaling agent (the NPC being hoiked) will take. Two hoik paths dependent on the actuation state of a junction point can be used to build a flip-flop mechanism, which is used extensively in Terraria Computers.

Flip-Flops:

The in-game Terraria computer uses flip-flops, two examples of which are illustrated here:

[IMG]

The basic idea of a flip flop is as follows: an NPC will pass through a hoik junction, and activate a pressure plate that changes the actuation state of a hoik tooth at that junction. The subsequent NPC will take the alternate path at that junction, and activate a pressure plate that once again changes the actuation state of the hoik tooth at that junction. In the left flip flop illustrated above, the hoik tooth at the junction point is deactuated, which will propel the summoned skeleton all the way to the right, passing over the pressure plate linked by red wire to that hoik tooth and actuating it. A subsequent skeleton will be hoiked upwards by the up hoik at that junction, passing over the pressure plate also linked by the same red wire to the hoik tooth at the junction.

The flip flop on the right is more compact, and is the one used in the registers shown below.

ALU Registers - Storage of Binary Info

The Terraria Computer featured in the video is an Arithmetic Logic Unit (ALU) capable of performing basic arthmetic operations (addition, subtraction, multiplication, division). To understand how the ALU crunches numbers, it is first essential to understand the components that make up the ALU. The ALU consists of three registers: the Accumulator Register, the Memory Register, and the MQ Register. Here is how the registers are constructed:

[IMG]

The Accumulator Register:

The accumulator register serves to accumulate information transferred to it from memory, and it will contain the output to most calculations done by the ALU. It is a binary counter, and consists of flip-flops joined together in a chain. In the schematic above, the accumulator is 5-bit, and stores a number between 0 and 31 depending on the actuation state of hoik teeth at each flip-flop junction. For each bit, the 0 state is denoted by an actuated hoik tooth (and torches that are off), while a 1 state is denoted by a deactuated hoik tooth (and torches that are on). Activating the switch linked by blue wire to the skeleton statue and the two teleporters sends a skeleton into the binary counter, increasing the number stored in the accumulator by 1. The stored number can also be manipulated by the levers connected by red wires to the hoik teeth at the junctions.

The teleporters that the skeletons enter when hoiked up send the skeleton to the lava trap in the schematic, but when the accumulator is linked with other devices the skeleton will be teleported elsewhere (see below). Note that when multiple teleporters are linked by wire, the NPC is always sent to the furthest teleporter, with the distance measured in terms of wire length, not actual in-game distance.

The MQ Register:

The MQ register controls how many times an operation is to be performed; in the ALU, it controls how many times the content of memory will be transferred to the accumulator. The MQ register is a reverse binary counter - it is constructed in the exact same manner as the accumulator except that all hoik teeth at the junctions are in the deactuated state to begin with. In other words, the 0 state of a bit is denoted by a deactuated hoik tooth, while a 1 state of a bit is denoted by an actuated hoik tooth. If a number is input into the MQ register, then each time a skeleton is sent into the register it will lower that number by 1.

The Memory Register:

The memory register stores information that doesn't get altered over the course of the ALU's operation. The only way to change the memory is by external means (inputting values with levers, transferring data from other registers, etc.). In the memory register depicted above, the 0 state of each bit is denoted by a pair of deactuated blocks that serve as a ceiling over a pair of up hoik teeth (preventing the skeleton from being hoiked upwards), while the 1 state of each bit is denoted by an actuated state, opening up the top path to the skeleton.

The memory register has a distributor attached to it that will scan memory, and transfer memory information to a linked accumulator (shown below) if any ceilings are open. When the skeleton enters the distributor initially, it gets hoiked upwards at the first junction, and a pressure plate deactuates the hoik tooth at that junction via the red wire. The skeleton is then hoiked to the immediate left into the teleporter, or hoiked past the open ceiling (shown below); the skeleton is subsequently teleported back to the teleporter at the start of the distributor. In the next cycle, the skeleton is hoiked upwards at the second junction, and this process is repeated until the skeleton has been hoiked upwards at every junction point. One finished, the skeleton exits from the distributor, passing over a pressure plate along the way that resets all the hoik teeth at each junction point back to their starting actuated state.

Register Combinations:

The registers can now be combined to allow for certain arithmetic operations. The simplest combination is between the accumulator and memory registers to allow for addition, and adding the MQ register allows for multiplication as well. Here is what the combinations look like:

[IMG]

Addition: Accumulator + Memory Register Combination

The mechanism on the left above depicts the merging of the accumulator and memory registers. The teleporters in the accumulator now send the skeleton back to the distributor (instead of sending the skeleton into a lava trap). Also, each bit in memory, running from least significant (1) to most significant (16), is lined up with the least to most significant bits in the accumulator. That means that if the bit with a value of 4 is in the "on" state in memory, than that value of 4 will be transferred to the accumulator at the bit that has a value of 4.

To add two numbers, one number needs to be input into the accumulator register via the levers below the number statues with yellow backgrounds, and the other number needs to be input into the memory register via the levers above the number statues with amber backgrounds. When the lever is pulled, the skeleton goes through the distribution system, transferring the number from memory to the accumulator. Since the accumulator is a binary counter, the number transferred is automatically added to the existing number in the accumulator. The process terminates once the skeleton exits the distributor in the bottom right corner, and gets hoiked into the lava trap.

Addition/Multiplication: Accumulator + Memory + MQ Register Combination

The mechanism on the right depicts the merging of all three registers. The wiring is now slightly changed to ensure that the skeleton is first sent into the MQ register, and not the distributor. The MQ register, being a countdown binary counter, will keep sending the skeleton into the distributor (via the teleporters when the skeleton gets hoiked upwards in the MQ register) to cause the contents of memory to be added to the accumulator as outlined previously. Thus the mechanism cycles between the MQ register and the distributor, until the countdown in the MQ register reaches 0. At that point, the skeleton will pass straight trough and into the lava trap in the bottom right corner, terminating the process.

This is thus the basis behind multiplication. If for instance, 0 is present in the accumulator register initially, 14 is input into the memory register, and 3 is input into the MQ register, then 14 will be added to the accumulator 3 times, resulting in a value of 42 in the accumulator when the process ends.

Complement System:

For subtraction and division, certain tricks have to be used since the mechanism is limited to only adding information from memory to the accumulator. The trick employed in subtraction and division is to take the complement of a number stored in the accumulator register. The complement can be determined by taking the maximum possible value that can be stored in the accumulator, subtracting the current value that is input, and then adding 1 to the result. So, for instance, if the accumulator is 5-bit (maximum value that can be stored is 31), and we added 13 to the accumulator, then the complement of 13 would be 31-13+1 = 19. The reason for doing this is explained below.

First, here is how the complement is implemented:

[IMG]

The actual subtraction of the input number from the maximum is achieved by simply reversing the polarity of all the hoik teeth and all the torches. This is done through the C lever in the schematic above, which connects via blue wire to all the torches and hoik teeth of each bit in the accumulator. To add 1 to the outcome of the subtraction, a skeleton is sent once into the accumulator - the blue wire from the C lever also connects the skeleton statue and the teleporter at the start of the binary counter.

Register Combinations with Complement Systems:

[IMG]

Addition/Subtraction: Accumulator and Memory Registers + Complement System

The Set-up for addition and subtraction is presented on the left in the schematics above. The merging of the accumulator and memory is identical to the set-up discussed earlier, but now a complement system has been added. Since the merge involves sending skeletons from the accumulator to the distributor, this needs to be stopped from happening if the complement of a number is taken. This is accomplished by a lava trap in the lower left corner. When the C lever is pulled, a skeleton that would otherwise go into the distributor would instead be hoiked upwards into the lava trap just before the distributor because pulling the C lever would actuate a hoik tooth at the teleporter before the distributor. Submerged in the lava is a pressure plate that connects via blue wire to that hoik tooth, so once the skeleton is killed off any subsequent skeletons arriving at that teleporter will proceed into the distributor as always.

Here is the trick for subtraction: the complement of a number in the accumulator will allow the addition of the number stored in memory to add and roll over the number in the accumulator. Thus we can generate a subtraction, even though we're still adding from memory to the accumulator. For instance, let's suppose we want to do 25 minus 10. We will need to input the larger number, 25, into memory, and the smaller, 10, into the accumulator. We then take the complement of 10, which will turn out to be 31-10+1=22. The significance of that 22 is that it is 9 away from the maximum value of 31. So, when we add 25 from memory to the accumulator, 9 of that 25 will go towards reaching the maximum of 31, 1 of that 25 will go towards rolling over from 31 to 0, and the remaining 15 of that 25 will go towards raising the accumulator value from 0 to 15. 15 is the correct answer to the subtraction.

This is also why we need to add 1 when we take the complement - it is to account for the fact that when rolling over from 31 to 0, we "lose" 1 in the process.

Addition/Subtraction/Multiplication/Division: Accumulator + Memory + MQ Registers + Complement System

Finally, let's examine the set-up for the full ALU, which is depicted on the right in the schematics directly above. The three registers are merged as discussed earlier, but two additional levers have been added to enable division. The first lever to the right just below the letter "Q" is used to transferm the MQ register from a countdown binary counter, to a count-up binary counter. In other words, the MQ lever is transformed into the accumulator for the purposes of division. This is accomplished simply by reversing the polarity of every hoik tooth in the MQ register from a deactuated state to an actuated state. The second additional lever, to the left of the "Q", deactuates a hoik tooth in the accumulator register right at the end of the register, just past the most significant bit. This means that a skeleton that reaches that junction point will no longer get hoiked into the teleporter above, but instead will be hoiked into the lava trap, terminating any further operations. This is designed to prevent any roll-over - once the maximum value in the accumulator is reached, the operation terminates.

The reason for this desired termination of any further events can be illustrated with a sample calculation. Let's suppose that we wish to do 15 divided by 3. We need to input the larger number, 15, into the accumulator, and the smaller value into memory. We then need to take the complement of 15, which will result in 31-15+1 = 17. Next, we activate the system, and the skeleton first enters the MQ register, add 1 to the tally (remember, the MQ register is now a binary counter), and then enters the distributor as always, transferring 3 to 17 resulting in 20 stored in the accumulator at that point. After the first transfer of 3, the skeleton then enters the MQ register, bumping up the number there to 2, and then enters the distributor again. The 3 stored in memory will be added three more times to the accumulator to generate 29, and this will result in an additional 3 being added to the MQ register for a total of 5 thus far. Finally, 3 will again be added to the accumulator, but since 31 cannot be exceeded, no overflow will be possible and the system stops, and we are left with 5 in the MQ register, the actual answer to our starting division problem.

In short, when we took the complement of 15, we generated a number, 17, that was 14 away from the maximum of 31. 3 can only be added to 14 four times, and the fifth time will not be possible since the overflow is blocked. Since the system starts in the MQ register, and adds 1 to the register automatically, the answer ends up being 1 + the number of times that 3 could be added to 17 before reaching the overflow. This is how an actual ALU performs division.

Additional Comments:

To examine these mechanisms first-hand, download the tutorial world and either follow the directions in this write-up or the directions in the video. See if you can design your own registers (there are many ways of making them) and build your own ALU!

Here is what the entire ALU that I've built looks like, complete with reset tracks and a full binary-to-decimal converter (which I'll explain in a future video tutorial). Note that some of the functions I described above associated with each arthmetic operation are actually bundled into individual levers. See if you can make sense of the wiring associated with the three registers, and bonus points if you are able to figure out the rest of the wiring too.

Computer + Converter:

[IMG]

Wiring:

[IMG]

In this updated ALU, I was able to engineer single lever activations for all arithmetic functions, so there is no longer a need to separately pull a complement lever when doing subtraction or division, and there is no longer a need to add one to the MQ register when doing addition or subtraction. Taking complements and adding 1 to the MQ register are now done automatically when the appropriate levers are pulled.

Protocols for all arithmetic operations:

Multiplication (X times Y):

1) Pull the 0 lever to reset
2) Input X into Memory Register
3) Input Y into MQ Register
4) Pull M(ultiplication) lever

Answer will be displayed in the Accumulator Register

Division (Y divided by X):

1) Pull the 0 lever to reset
2) Input Y (dividend) into Accumulator Register
3) Input X (divisor) into Memory Register
4) Pull D(ivision) lever

Answer will be displayed in the MQ Register

Addition (X plus Y):

1) Pull the 0 lever to reset
2) Input X into Memory Register
3) Input Y into Accumulator Register
4) Pull A(ddition) lever

Answer will be displayed in the Accumulator Register

Subtraction (Y minus X):

1) Pull the 0 lever to reset
2) Input Y (the larger value) into Memory Register
3) Input X (the smaller value) into Accumulator Register
4) Pull S(ubtraction) lever

Answer will be displayed in the Accumulator Register

X . IIIIIIII

Flip-Flops and the Art of Computer Memory

Keyboard Flip-Flop — It may surprise you to learn that flip-flops are an integral part of computing. Just… not the kind of flip-flop you think. (source)

This is the fifth part in my multi-part series on how computers work. Computers are thinking machines, and the first four parts of my series have been on how we teach computers to think. But all of this logic, electronic or otherwise, is useless unless our computers can remember what they did. After logicking something out, a computer needs to remember the result of all that logicking!
In this post, I describe how to use the logic gates described in part four to electronically implement computer memory.
This post depends heavily on my last few posts, so if you haven’t read them, you might want to.

In the first and second parts, I describe the language of logic that computers use, called Boolean algebra.
In the third and fourth parts, I describe one physical (albeit outdated) way that we can implement Boolean logic electronically.

Still here? Okay. Let’s get to it!

How Computer Memory Should Work

Before we talk about exactly how we implement computer memory, let’s talk about what we want out of it.

In the world of Boolean logic, there is only true and false. So all we need to do is record whether the result of a calculation was either true or false. As we learned in part three, we represent true and false (called truth values) using the voltage in an electric circuit. If the voltage at the output is above +5 volts, the output is true. If it’s below +5 volts, the output is false.
So, to record whether an output was true or false, we need to make a circuit whose output can be toggled between + 5 volts and, say, 0 volts.

Logic Gate, Logic Gate

To implement this, we’ll use the logic gates we discussed in part four. Specifically, we need an electronic logic gate that implements the nor operation discussed in part two. A nor B, which is the same as not (A or B), is true if and only if neither A nor B is true. We could use other logic gates, but this one will do nicely.

As a reminder, let’s write out the truth table for the logical operations or and nor. That way, we’ll be ready to use them when we need them. Given a pair of inputs, A and B, the truth table tells us what the output will be. Each row corresponds to a given pair of inputs. The right two columns give the outputs for or and nor = not or, respectively. Here’s the table:

truth table for OR and NOR — The truth table for the logical operations “A OR B” and “A NOR B.” Each row corresponds to a different set of inputs A and B; the last two columns correspond to the appropriate outputs.

Let’s introduce a circuit symbol for the nor gate. This will be helpful when we actually draw a diagram of how to construct computer memory. Here’s the symbol we’ll use:

a nor gate — A symbol for a NOR gate. The two terminals on the left correspond to the inputs. The terminal on the right corresponds to the outputs.

Crossing the Streams

Okay, so how do we make computer memory out of this? Well, we take two nor gates, and we cross the streams…

We define two input variables, which we call S (standing for set) and R (standing for reset), and two output variables, which we call Q and not Q. The reasons for this peculiar naming scheme will become clear in a moment. Then we wire the output of each of our nor gates so that it feeds back into the other nor gate as an input, as shown below.

For reasons that will eventually become clear, this circuit is called an SR-Latch, and it’s part of a class of circuits called flip-flops. Now let’s see if we can figure out what’s going on. Assume that both S and R are false for now. And let’s assume that Q is true and not Q is (as the name suggests) false, as shown below.

SR latch Q state — An SR latch such that the Q state is true, the NOT Q state is false, and both S and R are false. This state is self-perpetuating. Blue indicates FALSE. Red indicates TRUE.

Is this consistent with the truth table we listed above?

S nor Q is false, because if Q is true, then (obviously) both S and Q aren’t false. Since we gave the name “not Q” to the output of S nor Q, this means not Q must be false. That’s what we expected. Good.
R nor (not Q) is true, because R is false and not Q is false. The output of R nor (not Q) is the same as Q, so Q must be true. Also what we expected!

Okay, so what does this mean? It means that if we start our circuit in this state, with R and S as false, Q as true, and not Q as false, our circuit perpetuates itself in this state. Nothing changes.

Toggle Me This, Toggle Me That

Now let’s alter the state described above a little bit. Let’s change R to true. Since R is true, this changes the output of R nor (not Q) to false. So now Q is false…and since S is still false, the output of S nor Q is now true. Now our circuit looks like this:

SR_latch_not_Q_toggle — An SR latch mid-toggle. We set R to true. Immediately, Q becomes false, which causes NOT Q to become true.

And if we wait a moment further, the cross-wiring takes effect so that both inputs to R nor (not Q) are true. This doesn’t change the output, though, as shown below.

SR_latch_not_Q_toggle_2 — An SR-latch mid-toggle. After NOT Q becomes true, it feeds back into the first NOR gate. Fortunately, this doesn’t seem to affect anything.

Now we can set R to false again, and Q will stay false and not Q will stay true, as shown below.

SR_latch_not_Q — An SR-latch with Q false and NOT Q true. We got to this self-sustaining state by temporarily setting R to true.

Look familiar? This is the mirror image of the state we started with! And it’s self-sustaining, just like the initial state was. With both R and S set to false, not Q will stay true as long as we like.
Although R is false now, the circuit remembers that we set it to true before! It’s not hard to convince ourselves that if we set S to first true and then false, the circuit will revert to its original configuration. This is why the circuit is called a flip-flop. It flip-flops between the two states. Here’s a nice animation of the process I stole from Wikipedia:

SR latch animation — An animation of the flip-flop process for the NOR-gate based SR-latch we talked about. In this animation, RED signifies TRUE and BLACK signifies FALSE. (source)

This is computer memory. And similar devices are behind your CPU cache and other components inside your laptop.

A Whole World of Flip-Flops

Although it’s technically correct, generally, people don’t refer to the circuit I described as a flip-flop. The things people usually refer to as flip-flops usually only change state based on some sort of timer or clock. However, the idea is essentially the same.

In general, clocks are something I didn’t touch on. Real computers use a clock to sync the flipping of memory with the computations they perform using the logic gates I talked about earlier. (Clocks can also be generated using logic gates. This is the speed of your CPU clock.) I figured I wouldn’t go into that here because it’s a bit too technical and, in my opinion, not necessary for understanding.

Next Time

We now have enough tools to understand the essentials of how a computer works. It performs logical operations using logic gates, and it remembers what it did using flip-flops. Next time, we’ll take a break from electronic computers to discuss some other ways you can make a computer. Did you know you can make a computer with gears? With ropes and pulleys? With dominoes? With card games? Find out more next time.

Further Reading

Flip-flops are the domain of electrical engineers, so there’s not much non-technical material on them. Here’s what I could find.

A flip-flop is a special case of a class of circuits called “bi-stable vibrators.” If you like, you can learn about them on their Wikipedia page.
Here’s a fairly technical video lecture on flip-flops.
This set of lecture notes is at about the same level as my post, but it goes into substantially more depth.
If you want to understand clocked flip-flops, you might start here.

X . IIIIIIIII

The Boolean Circuit and Electronic Logic

Circuit Board Snake — This sculpture by Peter McFarlane embodies the fear a lot of us feel regarding the innards of a computer. If we touch it, it might bite! Have no fear. Today we learn what all those wires on that board do.

This is the fourth part in my multi-part series on how computers work. Computers are thinking machines, but they can’t do this on their own. We need to teach them how to think. And for this, we need a language of logic. In the first part of the series, I introduced this language of logic, Boolean algebra. In the second part, I described how to formulate complex logical statements using Boolean algebra. In the third part, I described how some of the electronics in old-school computers worked.
This time, I finally get to the meat of things. I describe how you can use the circuits described in part 3 to actually implement Boolean logic electronically.

Voltages

The following discussion is going to depend heavily on an understanding of the triode vacuum tubes that I discussed last time. So if you haven’t already, you probably want to last week’s article before you read this one.

That said, some review is probably in order. First let’s review electric voltage. The salient points are this. Electrons want to flow from places in a circuit that are at low voltage to places that are at high voltage. Voltage is measured in volts. We want to use voltage as a stand-in for the truth values described in parts one and two of my series on how computers work.

There are a number of ways we can use voltage to represent truth values. But let’s pick the most common way. Let’s say we have a circuit. We’ll connect a voltage-measuring device to a spot on our circuit—perhaps where two wires intersect—and say that, if it reads any voltage higher than +5 volts, then our circuit represents true at that spot. If it reads any lower, then our circuit represents false there.

(There’s an important detail I’m skipping here. Voltages are not absolute numbers. We know that electrons flow from low voltage to high voltage. But we need a baseline for what “zero volts” means. In every circuit, this “zero volts” value might be different, but we always have to set it and choose a value. We usually call “zero volts” ground.)

Vacuum Review

Now let’s review the basics of a triode. As the name suggests, a triode is a circuit component with three terminals, called the cathode, anode, and filament, as shown below. There’s another piece called the called the heating element that we won’t discuss in much detail.

triode schematic 1 — A schematic of a triode.

I discuss the triode in great detail in last week’s article. But for now, here’s what you need to know. The filament controls the flow of electrons from the cathode to the anode. Suppose that I hook up the triode in a circuit so that the anode is at a high voltage, and the cathode is at a low voltage. Then if the filament is at a low voltage like the cathode, then no current will flow. If the filament is at a high voltage like the anode, then current will flow.

Fiddly Names

It’s worth noting that the pieces of a triode can have other names. The cathode is often called the plate and the filament is often called the grid. In this naming scheme, confusingly, the heating element is often called the filament.

It’s also worth noting that these days triodes have been almost completely replaced by transistors.But transistors have different names for these parts. In a transistor, the cathode is called the source, the anode is called the drain, and the filament (or grid) is called the gate. A transistor does not have a heating element. To avoid confusion, I’ll use vacuum tubes instead of transistors. And I’ll use the names in my diagram.

Boolean Circuity

Now let’s implement Boolean logic! To do this, let’s chain some triodes together, as shown below.

an or gate implemented using vacuum tubes — An or gate made out of triodes. We keep the anodes at a very high voltage, much higher than the cathodes could possibly be at. Then we connect both cathodes to a terminal that we call “C.” We name the filament terminals “A” and “B” respectively.

Here we keep the anodes at a very high voltage, much higher than the cathodes could possibly be at. We then connect both cathodes to a terminal that we call C. We name the filament terminals A and B respectively.

Now let’s manipulate the terminals A and B and see what terminal C does.If both A and B are at a low voltage (i.e., false), then current won’t flow through either triode. The result is that C stays at a low voltage, which we’ll call false. But now let’s put terminal A at a higher voltage, say true. (For now we’ll leave B as false.) Then current will flow through the left-most triode and raise the voltage at terminal C so that it becomes true.

Similarly, if we keep A at a low voltage (i.e., false) but raise the voltage at B so that it becomes true, then current will flow through the right-most triode. This too will raise the voltage at terminal C and make it true. And of course, if both A and B are true, then current will flow and raise the voltage at C, making it true.
So if both A and B are false, then C is false.But if either A or B or both A and B are true, then C is true too. The astute among you might recognize C as the result of the logical operation A or B. We’ve just made the logical or work electronically! The circuit we just constructed is called an or gate.

More Gates

Can we do the same thing to make a logical and? Let’s try. We’ll still use two triodes. But now let’s connect them in a different way, as shown below. We put the anode of the first triode at a very high voltage. But we connect its cathode to the anode of the second triode. We label the filaments A and B respectively and the cathode of the second triode C.

An and gate implemented with triodes. We keep the anode of one triode at a very high voltage. But we connect the cathode to the anode of a second triode. We call the filament terminals “A” and “B” respectively and the cathode of the second triode “C.”

Now current will be unable to flow unless both terminals A and B are at a high voltage. In other words, C will be true only if both A and B are true. You might then recognize C as the output of the logical A and B, which we’ve now implemented electronically! This circuit is called an and gate.

Gates in Practice

I showed you how to electronically implement the boolean operations and and or described in George Boole and the Language of Logic, Part 1. If we wanted to make composite statements as we did in part 2, then we’d also need the not operator. But that’s actually a bit trickier (though not impossible) to make electronically. So I won’t describe it.

Usually, in practice, people use nand and nor gates as opposed to and, or, and not. These are harder to make, however, so I won’t describe them. Hopefully the gates I did describe, however, give you a feel for how this works.

Electronic Caveats

In my description of the and and or gates, I claimed that when current flowed through a triode, the voltage at the cathode changed. In practice things are a lot more complicated. Voltage and current are related. In simple cases, the relationship is given by Ohm’s law, which many of you are probably familiar with. In more complicated cases, where the current changes quickly, you need to take more things into account, like the travel time of electrical signals.

That said, the description I gave gets the basic idea across and, if we added more circuit components (such as, capacitors, inductors, and resistors), the gates I described would work.