Numerical Analysis

Numerical analysis is the study of algorithms to solve problems in continuous mathematics (as distinguished by discrete mathematics) .
Numerical Methods is a sub-field of mathematics called finishing of Linear Algebra, Calculus and Discrete Mathematics.
Numerical analysis
preliminary
The term comes from the Latin models mode (size). The model is a representation of an object or a real problem. To model a real problem, it can be used a systems approach.
First of all the issue is seen as a system consisting of a collection of sub-sub-system objects are generally independent from each other. These objects are physical entities or concepts that have certain characteristics or attributes.
The real issues facing the often complex. Because it is very difficult to represent all the characteristics present in the system into the model. In other words, in the process of characterization system simplified by only considering the attributes or factors that are relevant to the desired destination. As a result, a model because it is a representation of a system, it will have an overall information held by the system to be modeled.
Mathematical Model
To understand the meaning or definition of a mathematical model, we must understand the definition of the model itself. mathematical model revealed that: "is a model of an object or a concept that is used to represent something else. It ts reality scaled down an converted to a form that we can comprehend. " From these expressions can be seen that the model can be a physical object (an object) or abstract object(Concept) created to represent something. The model is made to something that is easy to understand.
The mathematical model is an integral part in problem solving techniques. Lots, mathematical models are derived from the techniques and principles of science, while at other times the model can be obtained from experimental data.
Establishment of a mathematical model is the process of translating a physical model of a phenomenon in a mathematical form. This process is a way to extinguish the quantities involved in physical phenomena with mathematical quantities. Scale - scale of mathematics were written using symbols - symbols of mathematics. And, the laws of physics that apply on the phenomenon expressed in the language of mathematics (equations).The language of mathematics that involves some of the concepts in mathematics, among other things, a function, differential, integral, and vector calculus. In addition, the concept of the tensor, differential topology, differential equations, differential geometry, and so on. The mathematical concepts can always be understood as having various physical interpretation.If a mathematical model in the form of differential equations, then the problem is how to determine the solution (settlement) of the differential equations. However, it should be realized that not all of the mathematical model in the form of differential equations have analytical solutions, especially when reviewing Persia differential equation because it involves several variables (variables). Therefore, the determination of the solution through a numerical approach (computing) to the problem is often done since the invention of the computer.Numerical methods
The technique used to formulate mathematical problems that can be solved with a count of operating / ordinary arithmetic. Solution figures obtained from a numerical method is approximately correct solution / solution approach (approximation) with a level of accuracy that we want. Because it does not exactly represent the actual solution, there is a difference between the two was then called the error / error.
Numerical methods to resolve the matter in the real world are often non-linear, in the form and process of sticking with the analytical method .
Why Using Numerical Methods
Not all mathematical problems or calculations can be solved easily.
It takes a method using the approach analyzes the problems of non-linear to produce the expected value.
Difficulty using the analytical method to find the exact solution to the huge amount of data, necessary for computing, - numerical methods essential actually For solve this problem
The use of analytical methods sometimes difficult to translate into an algorithm that can be understood by computers. Numerical methods are indeed departed from use of tools count is a good alternative in solving the problems of complex calculations.
Some Completion Criteria Mathematical Calculations
If the problem is a simple issue or there unproved mathematical analysis that can be used to solve the problem, the solution of mathematical (analytical method) is the exact settlement should be used. This settlement was the template for the use of the method of approach.
If the issue is very difficult or impossible to be solved mathematically (analytic) because there is no analysis of the mathematical theorems that can be used, it can be used a numerical method.
When the problem has been an issue that has a high complexity, so the numerical method was not able to disclose the settlement properly, it can be used methods of simulation.
Principles of Numerical Methods
This numerical method is presented in the form of algorithms that can be calculated quickly and easily.
The approach used in the numerical method is an approach to mathematical analysis, with additional graphics and easy calculation techniques.
Algorithms on numerical methods, the approach is the algorithm that algorithm appears the term iteration is the repetition of the calculation process.
With this method of approach, of course, any value calculation results will have an error value (an error value).
Numerical analysis naturally be applied in all fields of engineering and the physical sciences, but in the 21st century, life sciences and the arts began to adopt elements of scientific computing. Ordinary differential equations appeared in the movement of celestial bodies (planets, stars and galaxies. Optimization appears in portfolio management. Numerical linear algebra is very important in quantitative psychology. Stochastic differential equations and Markov chains essential in simulating living cells in medicine and biology
Before the advent of modern computers numerical methods often depends on interpolation using the large table is printed. Since the mid 20th century, instead, the computer calculates the required function. But interpolation algorithm may still be used as part of the software for solving differential equations.
general introduction
The overall objective is to design the field of numerical analysis and analytical techniques to obtain an accurate approximation solutions to difficult problems. Examples of these problems will be presented below.
Advanced numerical methods are essential in making numerical weather forecasting decent
The calculation of the trajectory of spacecrafts requires accurate numerical solution of ordinary differential equations system.
Automotive companies can improve vehicle safety by using a vehicle crash simulations. Simulations like this basically consists of solving partial differential equations numerically.
Institutions private investment funds using the tools of the entire field of numerical analysis to calculate the value of stocks and derivatives are more precise than other market participants
Airlines use sophisticated optimization algorithms to decide ticket prices, airplane and crew assignments and fuel purposes. This field is also called operations research
Insurance companies use numerical programs for actuarial analysis.
History
Field of numerical analysis had been developed centuries before the invention of the modern computer. Linear interpolation has been used for more than 2000 years ago. Many great mathematicians of the past preoccupied by numerical analysis, as is obvious from the name of important algorithms like Newton's method, Lagrange interpolation polynomial, Gaussian elimination, or Euler's method.
Great books containing formulas and tables of data such as interpolation points and function coefficients created to facilitate the hand calculation. By using this table (often featuring the calculation to 16 decimal places or more for some functions), we can see the values to be filled into the formulas given and achieve very good numerical estimates of some functions. The main work in this field is the N I S T publication edited by Abramovich and Stegun, a thick book over 1000 pages. This book contains a lot of commonly used formulas and functions and values at many points. Value f-value function is no longer very useful when a computer is available, but the list may still be very useful formula.
Mechanical calculator was also developed as a tool for hand calculations. These calculators evolved into electronic computers in 1940. Later it was discovered that the computer is also useful for administrative purposes. But the invention of the computer also influenced the field of numerical analysis, because it allows the calculation of longer and more complicated.
Direct methods and iterative
Direct methods compute the solution to a problem in a finite number of steps. This method will give an answer in a matter of exactly when done with infinite precision. Examples are Gaussian elimination, factoring QR method to solve systems of linear equations and the simplex method for linear programming. In practice, the accuracy of calculation used is up (floating point) and the results are approximations of the actual solution (with the assumption reached numerical stability).
Unlike the direct method, iterative methods are not expected to end in a finite number of steps. Starting from the initial guess, iterative methods produce approximations which successively converges to the exact solution. Convergence test is done to decide when a sufficiently accurate solution can be achieved. Even using infinite precision arithmetic once such a method will not generally reach a solution in a finite number of steps. Examples include Newton's method, the method for two, and Jacobi iteration. In computational matrix algebra, iterative methods typically required for large problems.
In the numerical analysis of iterative methods more common than direct methods. Some methods are essentially straight, but usually applied as if it is not, such as G M R E S and gradient method companions. For these methods the number of steps needed to achieve the exact solution is so large that approximations can be accepted as a method of iterative.
discretizing
Continuous problems must sometimes be replaced by a discrete problem whose solution is known approached continuous problem. Such a process is called discretization. For example, the solution is a function of differential equations. This function must be represented by a finite amount of data, for example by its values on a finite number of points in its domain, although the domain is continuants.
Creation and propagation error
Studies error is an important part of numerical analysis. There are several entrances to the error in solving a problem.rounding off
Rounding errors arise because it is impossible to represent the real numbers are inexact in a machine with infinite memory (all digital computers like this).Error beheading and discretizing
Error beheading done when an iterative method is terminated or a mathematical procedure approached, and solving different approximation to the exact solution. Similar to this, the discretization error occurs because solving discrete problems are not the same as a continuous problem solving. For example, at the iteration to compute the solving the equation 3 x 3 + 4 = 28 {\ display style 3x ^ {3} + 4 = 28} {\ displaystyle 3x ^ {3} + 4 = 28}, after 10 or so iterations, we conclude that the roots of approximately 1.99. Thus we have an error beheading 0.01.
Once the error was created, this error will spread to the entire calculation. For example, we have learned that the operation + on a calculator or a computer is not exact. Therefore the calculation of a + b + c + d + e is inexact again.
What does it mean when we say that the beheading error created when we approached a mathematical procedure? We know that in order to integrate the functionality we need to know the exact sum of the number of infinite trapezoid. But numerically we can only find trapezoidal sum up, and because it is simply approximation of the mathematical procedure. Similar to it, to derive a function, differential elements near zero, but numerically we can only pick up the value of the differential elements.
Software
Since the end of the twentieth century, most of the algorithms implemented in different programming languages. Netlib has a wide list of software that is widely used in numeric fields, most programming languages used in Fortran and C. For commercial software products implement a numerical algorithm that is more diverse, including IMSL and NAG libraries, while for a free alternative is the GNU Scientific Library ,
There are several popular software in numeric fields such as MATLAB, TK Solver, S - PLUS, LabVIEW, and IDL addition there is also a free version like freemat, Scilab, GNU Octave (similar to Matlab), IT ++ (C ++ library) , R (similar to S - PLUS) and certain variants of Python. The resulting performance of the software vary, for matrix and vector operations are usually quite fast, while for scalar speed varies by an order of magnitude.
Many computer algebra systems such as Mathematica software has advantages in terms of arbitrary precision arithmetic so that it can provide more accurate results.
In addition the software lembatang spread also be used to solve problems relating to numerical analysis .
X . I
Numerical Methods
There are six steps that must be done in solving problems with numerical methods, namely:
I. Modeling, all of the parameters in the problems modeled in the form of mathematical equations. Simplifying the model, a mathematical model was obtained in the first stage may still complex. To facilitate and speed up computer performance, the model is simplified by removing the parameters that can be ignored.
II. Formulation of numerical, after a simple mathematical model is obtained, the next step is to formulate numerically.
III. Develop an algorithm of a numerical method selected.
IIII. Programming, algorithms have been developed translated into a computer program, by first making a flowchart of his then written in the form of programs, such as M A T L A B.
IIIII. Operations, the computer program is executed with test data before using actual data.
IIIIII. Evaluation, when programs have been completed using actual data, the results are interpreted. Interpretation involves analysis and comparing the calculation results with the basic principles and empirical results to determine the quality of the numerical solution.
Definition of Numerical Methods
Numerical methods are techniques to solve problems that are formulated mathematically by means of operating a count (arithmetic).
Some definitions of numerical methods proposed mathematician, for example, a numerical method is a technique in which a mathematical problem is formulated such that it can be resolved by arithmetic operations; numerical method-engineering is a technique used to formulate mathematical problems that can be solved only with the count operation, which consists of surgery plus, minus, multiplication and division. There are many types of numerical methods, but basically, each - each of these methods have a common characteristic, which always includes a number of arithmetic calculations. So the numerical method is a technique to formulate mathematical problems that can be solved with arithmetic operations consisting of surgery plus, minus, multiplication and division.
Why Should Numerical Methods?
The reason is the use of numerical methods because not all mathematical problems or mathematical calculation can be solved easily. Even in the principles of mathematics, a mathematical problem that most first seen is whether this issue has a settlement or not.
Why Should Numerical Methods?
The reason is the use of numerical methods because not all mathematical problems or mathematical calculation can be solved easily. Even in the principles of mathematics, a mathematical problem that most first seen is whether this issue has a settlement or not.
So, if a problem is very difficult or impossible to complete with mathematical methods (analytic) then we can use numerical methods as Alternative settlement of the issue.
II. Principles of Numerical Methods-> Used if the analytical method can not be used again-> Numerical Methods is a problem-solving approach to getting that can be justified analytically-> The approach is a mathematical analysis-> Numerical Methods consists of algorithms that can be calculated quickly and easily-> Because it comes from the algorithm approach, then this will wear Numerical Methods iteration (repetition)-> Value error is the most important thing to know how well the method used.
III. Use of Numerical MethodsUse of Numerical Methods usually done to resolve the problem mathematically difficult settlement obtained using analytical methods, namely:a. Resolving the non-linear equationsb. Resolving simultaneous equationc. Resolving differential and integrald. Interpolation and Regressione. Solve differential equationsf. Multi-variable problem to determine the optimal value of unconditional
IIII . Uses Numerical Methods
In addition there are a number of reasons why people use numerical methods for solving the problems that it faces. Some of the reasons are as follows.
Numerical method is a technique to solve mathematical problems effectively and efficiently. With the help of a computer he can handle complex problems and involves extensive calculation y ang, for example, to solve the problem not the solution of a linear equation, a large system of equations, and other issues included in the technical and social. Problems are often difficult or even impossible can be solved analytically can be solved by numerical methods.
There are many different packages of computer programs (eg Excel, maple, matlab, or other package programs) available and traded so easily acquired in operation include numerical methods. Thus, fixers simply adjust to the characteristics of the package programs with algorithms used in solving the problem.
If the problems faced tough resolved with the help of a computer program package, then the troubleshooters can use a computer program (eg, Basic, Pascal, Fortran, or other computer programs). If the troubleshooter proficient designing its own program, the troubleshooter can be freer use of numerical methods for solution with her problems.
On the other hand, a numerical method is a kind of efficient means to get to know the characteristics of the computer and design algorithms, flowcharts and writing computer programs themselves.
X . II
NUMERICAL METHOD: Theory and Numerical Methods Usability
In the method of solving problems in a variety of disciplines, such as in the fields of physics, chemistry, mathematics or economics, or the problems in the field of engineering (engineering), Such as Civil Engineering, Mechanical Engineering, Electrical, and so on, among others, in general, should be formulated in mathematical notation before analyzed qualitatively both analytically (in the exact sciences) or numerically, although there are several others using the settlement method empirically (by experiment ). Figure 1.1. Chart Completion Method analytic method is actually a method that can provide a real solution (exact solution) or a true solution means solving methods of mathematical models with algebraic formulas is standard (common) and the resulting solution has an error or error = 0. However, the analytical method only superior in a number of math problems are limited. Though the issues that arise in the real world often involve complicated forms and processes. As a result, the practical value of the completion of the analytical method to be limited. If the analytical method can no longer applied, the actual solution to the problem can still be found usingnumerical methods, Numerical method is a technique used to formulate mathematical problems that can be solved with the calculation operations / arithmetic usual (plus, minus, times, and for). Method means the way, while the means of numerical figures. So numerical methods literally means counting using numbers.From these explanations, there are two fundamental things about the differencebetween the numerical methods with the analytical method: first, a solution using numerical methods always a point with the analytical method generally produces a solution in the form of the mathematical function mathematical function can be further evaluated to produce a value in numerical terms. Second, by numerical methods, we only get a solution that approaches or approach the solution .
true so that the numerical solution is called also
solution approach, but the solution approximation can be made as precisely as we want. Approximation solution obviously is not exactly equal to the true solution, so there is a difference between the two. The difference is called the error (error) .
using Numerical Methods
• Not all mathematical problems or calculations can be solved easily.
• A method that uses analyzes the issue of non-linear approach to generate the expected value.
• Difficulty using the analytical method to find the exact solution to the huge amount of data, necessary for computing, numerical methods becomes important to resolve this
• The use of analytical methods sometimes difficult to translate into an algorithm that can be understood by computers. Numerical methods that are departing from usage count tools are a good alternative in resolving
problems of complex calculations.
Some of the criteria for the completion of the math
• If the problem is a matter of simple or no analysis mathematical theorem can be used to solve the problem, the solution of mathematical (analytical method) is the exact settlement should be used. This settlement was the template for the use of the method of approach.
• If the problem is very difficult or impossible to be solved mathematically (analytic) because there is no analysis of the mathematical theorem that can be used, it can be used a numerical method
. • If the problem has been an issue that has a high complexity, so the numerical methods were not able to present the settlement properly, it can be used methods simulation .
Stages Solving Problems NumericallyThere are six steps done in solving real world problems by numerical methods, namelyI. ModellingThis is the first stage. Modeled real world problems into mathematical equationsSimplifying modelsThe resulting mathematical model of phase 1 may be too complex, which include many variables (variable) or parameter. The more complex mathematical models, the more complicated the solution. Maybe some assumption is made that some parameters can be ignored. For example, air friction factor ignored so that the coefficients of friction in the model can be discarded.The mathematical model derived from the simplification becomes more simple so that a solution will be easier to obtain.II. numerical formulationAfter a simple mathematical model is obtained, the next step is to formulate numerically, among others: a. determine the numerical method to be used together with the analysis of the initial error ( the estimated errors, determining the step size, and so on). The choice of method is based on the following considerations: - whether the method thoroughly? - Whether the method is easily programmable and quick implementation time? - Whether the method is not sensitive to changes in the data are quite small? b. developing the algorithm of a numerical method selected.III. programmingThe next step is to translate the algorithm into a computer program using one programming language to master.
IIII. operationalAt this stage, the computer program is executed with test data before the actual data.
IIIII. EvaluationWhen the program has already been completed with the actual data, the results obtained are interpreted. Interpretation of the results includes the analysis run and compare it with the basic principles and empirical results to assess the quality of the numerical solution, and the decision to run the program with to obtain better results
Error (Error)
Numerically completion of a mathematical equation only gives an approximate value which is closer to the exact value (right) of the analytic solution.
There are three kinds of basic errors;
1. Error default
2. Error cutting
3. rounding error
Error congenital (Inherent)
That error in the value of the data and results from errors in copying the data, misread the scale or errors due to lack of understanding of the physical laws of the measured data.
example:
Measurement interval of 2.3 seconds:
• There are some errors because it is only by coincidence interval will be measured precisely 2.3 seconds.
• Some boundary errors inherent conceivable in mind:
• Due to an error in the data that is operated by a computer with some numerical procedures.
Cutting error (truncation error)
• Liaise with the method of implementation of numerical procedures
• Examples of the infinite Taylor series
In the numerical calculation of this error is criticalRounding error• Due to rounding• Occurs in a computer provided some specific figures for example; 5 points:• The sum of the results 16.4279 9.2654 + 7.1625
It comprises six numbers that can not be stored in our computer and will be rounded up 16.428
Destination results of the use of numerical methods• numerical method is a technique used to formulate mathematical problems that can be solved with the calculation operations / arithmetic usual(Plus, minus, times, and for).• numerical methods, we only get a solution that approaches or approach the true solution so that the numerical solution is called alsosolution approach (approximation)
,• Stages Solving Problems Numerically ie modeling, simplifying the model, programming, operation, evaluation• Completion numerically from a mathematical equation only gives an approximate value which is closer to the exact value (right) from the analytic solution, which is the default Error, Error cutting, rounding error.
X . III
Numerical Methods for Electrical Engineering
With the rapid development of technology and the progress of the times, we need a product with high precision and accuracy, and processing time is short. So also with problems in the field of pure science and applied physics. In a calculation with numerical data requires precision and good accuracy.
At the time of information technology has not advanced rapidly, practitioners and professionals in the fields of engineering and science analyzes with manual calculations. Simplification is used where a very complex structure simplified into a simple structure. This is done to avoid difficulties in the analysis.
Often, mathematical modeling appears in a form that is not ideal, so it can not be solved by using the analytical method to obtain a true solution (exact solution).
By using a numerical method, exact solutions of the problems faced will not be obtained. Numerical methods can only provide a solution that is approaching or approached the true solution so that the numerical solution is also a solution called approximation (approximation solution). This solutions approach is certainly not exactly the same as a true solution, so there is a difference between the two.
The rapid development of computational techniques (computer systems and software), which looks over the last decade, has allowed for the automatic processing of data within the scope of many important human activities, such as science, technology, economics, and workers' organizations. Within the scope of technology, this development led to the separation of the computer used as the design and manufacturing processes consisting of :
- Computer-aided design (CAD)
- Computer-aided manufacture (CAM)
In the application used numerical formulations of the finite element method to solve mathematical problems. Here is a book that presents a finite element techniques in solving electrical engineering problems with the application. Fundamental Numerical Methods for Electrical Engineering .

Field of numerical analysis had been developed centuries before the invention of the modern computer. Linear interpolation has been used for more than 2000 years ago. Many great mathematicians of the past preoccupied by numerical analysis, as is obvious from the name of important algorithms like Newton's method, Lagrange interpolation polynomial, Gaussian elimination, or Euler's method.Numerical analysis naturally be applied in all fields of engineering and the physical sciences, but in the 21st century, life sciences and the arts began to adopt elements of scientific computing. Ordinary differential equations appeared in the movement of celestial bodies (planets, stars and galaxies. Optimization appears in portfolio management. Numerical linear algebra is very important in quantitative psychology. Stochastic differential equations and Markov chain is important in stimulating living cells in medicine and biology.Mechanical calculator was also developed as a tool for hand calculations. These calculators evolved into electronic computers in 1940. Later it was discovered that the computer is also useful for administrative purposes. But the invention of the computer also influenced the field of numerical analysis, because it allows the calculation of longer and more complicated. Another important application is the atmospheric modeling. In addition to improving weather forecasts, the model is very important to understand the possible effects of human activities on the earth's climate.As we know, the development of computers increasingly larger starting speed in reading a command given user until the shape is now more practical and easy to carry anywhere at any time because the size is so small that we can enter into the pocket. But apart from that, the computer today was the speed in reading a command is getting faster, this is not another because the basic formula of computer problems increasingly growing. It is therefore not surprising that computer day after day is growing. With the development of a computer, then it means we can do an activity that is usually complicated to be easy, one unit is in the process of calculation. In the old days it possible to perform a calculation of the banking, the number of residents, and others require a long time, this is due to lack of adequate facilities. But with the development of computers and also with programming languages such as VB, C ++, C #, PASCAL, and other programming languages we can use it all to make a calculation using the language according to our ability.In addition, the relationship between computers by numerical methods was nothing to do with the hardware devices on the computer. With the development of the computer, then from here, we can take a conclusion about the computer hardware device which is faster or slower. The method used here is to collect some samples computers that have different abilities and from here look for a formula of the hardware in order to get the formula of a hardware device. If it has been found, it will easily be made to the size of a computer that we want though very small in size but has a high ability as today we are used to. But the solution that we get only a solution that approaches or approach the true solution so that the numerical solution is also called approximate solution. This can be seen when we buy a computer device, such as flash. In the written statement the amount of capacity is 4GB, but apparently after being questioned about the amount of capacity is only 3,75GB. This means the flash is not 100% right 4GB but only 3,75GB approaching 4GB. But the solution approximation can be made as precisely as we want. Approximation solution obviously is not exactly equal to the true solution, so there is a difference between the two. The difference is called the error (error).
Numerical methods and numerical analysis is certainly not the same or has the distinction for a particular issue is not enough we just use the method to obtain the desired results; we also need to know whether such methods do provide solutions approximations, and how good approximation of it. This gave rise to a new study, the numerical analysis.
Numerical methods and numerical analysis are two different things. The methods are algorithms, concerning the steps to resolve the problem numerically, whereas the numerical analysis is applied mathematics to analyze methods. In numerical analysis, the main thing to be emphasized is the analysis of the error and the speed of convergence a method. Theorems of mathematics is widely used in the analysis method. In the course of this, we will incorporate some material such as errors of numerical analysis methods and the convergence of methods. The task of the analyst is to develop and analyze numerical numerical methods. This includes proving whether a convergent method, and analyzing the limits of error of numerical solution. There are many sources of error, including the level of accuracy of mathematical models, computer arithmetic system, and conditions used to stop the process of finding solutions. All of this must be considered to ensure the accuracy of the final solution are calculated.
Implementation of Computing in the FieldThis computational theory can be implemented into the field - a particular field. Implementation of fields - fields related to computing theory, namely:
Physics
Chemistry
Mathematics
economy
Geography
Geology
I . Implementation of the Chemical Sector
Implementation of modern computing in the field of Computational Chemistry chemistry is that the use of computer science to help solve chemical problems, for example, the use of super computer to calculate the structures and properties of molecules. The term theoretical chemistry may be defined as a mathematical description of chemistry, whereas computational chemistry is usually used when a mathematical method developed well enough to be used in a computer program. It should be noted that the word "right" or "perfect" does not appear here, as very few aspects of chemistry that can be calculated precisely. Almost all aspects of chemistry can be described in a qualitative or quantitative computational scheme approximations.
II . Implementation in Mathematics
Implementation of modern computing in mathematics there is an algorithm of numerical analysis is used to analyze the problem - a mathematical problem. Field of numerical analysis had been developed centuries before the invention of the modern computer. Linear interpolation has been used for more than 2000 years ago. Many great mathematicians of the past preoccupied by numerical analysis, as is obvious from the name of important algorithms like Newton's method, Lagrange interpolation polynomial, Gaussian elimination, or Euler's method.Great books containing formulas and tables of data such as interpolation points and function coefficients created to facilitate the hand calculation. By using this table (often featuring the calculation to 16 decimal places or more for some functions), we can see the values to be filled into the formulas given and achieve very good numerical estimates of some functions. The main work in this field is the NIST publication edited by Abramovich and Stegun, a thick book over 1000 pages. This book contains a lot of commonly used formulas and functions and value at many points. Value f-value function is no longer very useful when a computer is available, but the list may still be very used . calculator formula mechanics also developed as a tool for hand calculations.These calculators evolved into electronic computers in 1940. Later it was discovered that the computer is also useful for administrative purposes. But the invention of the computer also influenced the field of numerical analysis, because it allows the calculation of longer and more complicated.
III . Implementation at the Physics department
Implementation of modern computing in physics there Computational Physics is studying a combination of Physics, Computer Science and Applied Mathematics to provide a solution to the "Events and complex issues in the real world" either by using simulation also use the right algorithm. An understanding of physics in theory, experiment, and computation should be comparable, in order to produce a numerical solution and visualization / modeling the right to understand the problems of Physics.
To perform such work evaluating the integral, differential equation completion, completion of simultaneous equations, plot a function / data, making the development of a series of functions, finding roots of equations and working with complex numbers, which become the purpose of applying computational physics. Many software or language used, either MatLab, Visual Basic, Fortran, Open Source Physics (OSP), Labview, Mathematica, and others are used for understanding and finding the numerical solution of problems in computational physics.
Importance of Modern ComputingModern computing is a system that would solve mathematical problems using computers with how to construct algorithms that can be understood by the computer that is useful to solve a problem. In modern computing are calculations and finding solutions to problems. Calculation of modern computing are accuracy, speed, problems, large volume and complexity. This modern computing first proposed by a scientist named John Von Neumann. He was the one who first put forward the concept of a system that receives instructions, instructions and store them in a memory. The concept is the basis of modern computer architecture. John Von Neumann provides a variety of increased contribution by way of work - his work in the field of mathematics, quantum theory, game theory, nuclear physics, and computer science. In addition, Von Neumann was also a scientist who was very instrumental in the making of the atomic bomb at Los Alamos during World War II past. And thanks to the expertise Neumann in the field of game theory is he could give birth to the concept of automata, computational technology and modern atomic bomb that eventually gave birth to a computer.
X . IIII
computer science in data collection on numerical analysis in complex computer
( Computational Science and Engineering / CSE )
The Computer Science area conducts research in the following main areas :
Signal processing and computer vision.
In particular, algorithms for filtering and segmentation, perceptual
process modeling (stereo vision, motion perception, color perception,
etc.), image registration, robust transmission of images and video, image
analysis from optical experiments , calibration and camera positioning, etc.
Applications have been developed in bio medicine .
Numerical methods and optimization. This
includes multi-objective optimization with applications to practical
engineering problems, evolutionary algorithms and algorithms for the
estimation of distribution with applications to design and global and
restricted optimization, numerical solution of partial differential
equations, and numerical modeling using finite elements.
Robo . This includes motion planning and perception for mobile robo ,
feasibility conditions for the movement of mobile robo outdoors and
visual control of robo .
Multidimensional data analysis and pattern recognition. This
include statistical modeling, the exploration, prediction and
classification of large volumes of data, machine learning, information
transmission, databases, data mining and pattern recognition.
The Computer Science area organizes events and seminars with the
participation of leading national and international researchers. Regular
events, some with inter-agency collaboration, include the following:
- School of Modeling and Numerical Methods
- Workshop - School of Image Processing
- Workshop on Robotics and Motion Planning
- Conference on Neuro imaging
- Statistical Pattern Recognition Workshop
relationship between computers, engineering and mathematics :
CSE is a broad multidisciplinary area that encompasses applications in science/engineering, applied mathematics, numerical analysis, and computer science. Computer models and computer simulations have become an important part of the research repertoire, supplementing (and in some cases replacing) experimentation. Going from application area to computational results requires domain expertise, mathematical modeling, numerical analysis, algorithm development, software implementation, program execution, analysis, validation and visualization of results. CSE involves all of this.

One point we would like to emphasize in this document is that CSE
is a legitimate and important academic enterprise, even if it has
yet to be formally recognized as such at some institutions. Although it
includes elements from computer science, applied mathematics, engineering
and science, CSE focuses on the integration of knowledge and methodologies
from all of these disciplines, and as such is a subject which is distinct
from any of them.
- CSE makes use of the techniques of applied mathematics and computer
science for the development of problem-solving methodologies and robust
tools which will be the building blocks for solutions to scientific
and engineering problems of ever-increasing complexity. It differs from
mathematics or computer science in that analysis and methodologies are
directed specifically at the solution of problem classes from science
and engineering, and will generally require a detailed knowledge or
substantial collaboration from those disciplines. The computing and
mathematical techniques used may be more domain specific, and the computer
science and mathematics skills needed will be broader.
- It is more than a scientist or engineer using a canned code to generate and visualize results (skipping all of the intermediate steps).
Although some researchers have been doing what might now be called CSE research for quite some time, for a number of reasons we appear to be at a critical juncture in terms of the role being played by simulation in science and industry. Historically, simulation has been used as a qualitative guide for design and control, but has often not been expected to provide accurate results for realistic physical systems. Increasingly, simulation is being used in a more quantitative way, as an integral part of the manufacturing, design and decision-making processes, and as a fundamental tool for scientific research. Problems where CSE has played and is expected to continue to play a pivotal role include:
- Weather and climate prediction. Future energy and environmental strategies
will require unprecedented accuracy and resolution for understanding
how global changes are related to events on regional scales where the
impact on people and the environment is the greatest. Achieving such
accuracy means bringing the resolution used in weather forecasting to
the global predictions, which is not practical currently because of
the very large amounts of data storage and long computation times that
are required. A major advance in computing power will enable scientists
to incorporate knowledge about the interactions between the oceans,
the atmosphere and living ecosystems, such as swamps, forests, grasslands
and the tundra, into the models used to predict long-term change. Climate
modeling at the global, regional and local levels can reduce uncertainties
regarding long term climate change, provide input for the formulation
of energy and environmental policy, and abate the impact of violent
storms.
- Combustion. Accurate simulation of combustion systems offers the promise
of developing the understanding needed to improve efficiency and reduce
emissions as mandated by U. S. public policy. Combustion of fossil fuels
accounts for 85% of the energy consumed annually in the U. S. and will
continue to do so for the foreseeable future. Achieving predictive simulation
of combustion processes will require terascale computing and an unprecedented
level of integration among disciplines including physics, chemistry,
engineering, mathematics and computer science.
- Nuclear stockpile stewardship. While new weapon production has ceased,
the ability to design nuclear weapons, analyze their performance, predict
their safety and reliability, and certify their functionality as they
age is essential for conscientious management of the enduring U. S.
nuclear stockpile. Dramatic advances in computer technology have made
virtual testing and prototyping viable alternatives to traditional nuclear
and nonnuclear test-based methods for stockpile stewardship. Rudimentary
versions of virtual testing and prototyping exist today. However, to
meet the needs of stockpile stewardship for the near future requires
high-performance computing far beyond our current level of performance. The ability to estimate and manage uncertainty in models and computations
is critical for this application, and increasingly important for many
others.
- Simulation, design and control of vehicles. It is now standard practice
in the design of mechanical systems such as vehicles, machines or robots
to use computer simulation to observe the dynamic response of the system
being designed. Computer-aided design drastically reduces the need to
construct and test prototypes. Simulation is used not only to improve
performance, but also for safety and ergonomics. Real-time simulation
with operator in the loop and/or hardware in the loop presents substantial
challenges for algorithms and software.
- Aircraft design. Since the early days of computing, computational
simulation has been used in the performance analysis and design of aircraft
components, such as the analysis of lift and drag of airfoil designs.
As computations become more sophisticated and computers more powerful,
computational simulation is used as an essential tool in the complete
design process. For example, the Boeing 777 was the first jetliner to
be 100% digitally designed, using 3D solid modeling. Throughout the
design process, the airplane was pre assembled on the computer, eliminating
the need for a costly full-scale mark-up. CSE will play an increasing
important role in the entire design and analysis process as capabilities
improve for such things as numerical modeling of combustion for engine
design.
- Electronic design automation. Electronic design automation and CSE have long had a symbiotic relationship. Modern electronic systems (most notably the microprocessors that have enabled CSE to achieve its current prominence) are extraordinarily complex. The development of such systems is only possible with the aid of computational tools for simulation and verification of the systems as part of the design process. Computation plays an important role at all levels of electronic design, from simulating the processes used to fabricate semiconductor devices, to simulating and verifying the logic of a microprocessor system, to laying out the floor plan of VLSI circuitry.
- Biology. CSE technologies are rapidly becoming indispensable to the
biological and medical sciences. Simulation plays a major role in the
conceptual development of medical devices, both those used in diagnostic
procedures (electromagnetic, ultrasonic, etc.) and in design of artificial
organs (hearts, kidneys, etc.). Biomedical optics depend heavily on
computational modeling in uses in detection and treatment in oncology,
opthalmology, cardiology, and physiology. Computational modeling plays
a fundamental role in the emerging efforts to combine mathematics and
biology in the genomic sciences (genome sequencing, gene expression
profiling, genotyping, etc.). In this area one needs large scale simulations
with complex computational models to develop new theoretical/conceptual
models and understanding of molecular level interactions.
- Chemistry. Computational chemistry (CC) is widely used in academic
and industrial research. Computed molecular structures, e.g., very often
are more reliable than experimentally determined ones. According to
"Chemical & Engineering News," the newsletter of the American
Chemical Society, Computational Chemistry has developed from a "nice
to have"' to a "must-have"' tool . The main incentive
of CC is the prediction of chemical phenomena based on models which
relate either to first principles theory ("rigorous models"),
to statistical ensembles governed by the laws of classical physics or
thermodynamics, or simply to empirical knowledge. In real problem solving
situations, these models are often combined to form "hybrid models"
where only the critical part of the problem is treated at the rigorous
level of theory. Rigorous theory in the molecular context is synonymous
with quantum mechanics, i.e., solving the Schrödinger equation
for a molecular complex with or without the presence of external perturbation
(photons, electric fields, etc.). There are a number of methods available
which provide approximate solutions to the Schrödinger equation
(Hartree-Fock and Density Functional theory, e.g.). Simulation is used
to predict properties of large and complex entities such as a liquid,
the folding of a protein in solution, or the elasticity of a polymer.
Finally, empirical models most often try to establish correlations between
the structure of a molecule and its (pharmaceutical) activity. Simulations
and quantum chemical calculations, on the other hand, very often are
extremely compute-intensive due to the number of degrees of freedom
and the complexity of the terms to be evaluated. The high accuracy required
in these calculations sets restrictions with regard to the method used
to solve the partial differential equations (PDEs) involved. Further
information is available at the website for the International Union
of Pure and Applied Chemistry .
- Materials. The challenge in materials research is to invent new materials
and to perfect existing ones by fabrication and processing so that they
have the desired performance and environmental response . For example,
there are many new and important applications for thin films, including
silicon-based microelectronics, compound semiconductors, opto-electronics
devices, high-temperature superconductors and photovoltaic systems.
The growth of such thin films, which can be accomplished via processes
such as chemical vapor deposition (CVD), is sensitive to many factors
in the manufacturing process. Simulation is an essential tool for understanding
this process, and requires the development of mathematical models and
computational techniques. Process control, which is an order of magnitude
more computationally complex than simulation, is emerging as an essential
tool in fabrication . Recently, large scale complex computational
modeling has been used to design high pressure, high throughput CVD
reactors to be used as enabling devices in the production of new and
exotic materials.
- Bio engineering. Historically, engineers have used chemistry, thermodynamics, and transport to design chemical processes. Now these fundamental processes are applied to the understanding of complex biological phenomena that are governed by the same physical laws. Computer models are being used to understand and to develop treatments for glaucoma, to understand and to fabricate bio artificial materials for example bio artificial arteries, and for studying the normal and pathologic response of soft hydrated tissues in the human musculoskeletal system .
Growth in the expectations for and applications of CSE methodology has been fueled by rapid and sustained advances over the past twenty years of computing power and algorithm speed and reliability (see diagram below), and the emergence of software tools for the development and integration of complex software systems and the visualization of results. In many areas of science and engineering, the boundary has been crossed where simulation, or simulation in combination with experiment is more effective (in some combination of time/cost/accuracy) than experiment alone for real needs.

Mathematics and computer science
- Numerical analysis (linear algebra and optimization, ordinary and partial differential equations)
- Applied mathematics (ordinary differential equations, dynamical systems, partial differential equations, mathematical modeling)
- Computing (languauges / operating systems/networking ; parallel/distributed)
- Data Analysis (visualization, statistical methods)
X . IIIIII
Accurate Numerical Methods for Computing 2D and 3D Robo Workspace
Exact computation of the shape and size of robo ( ringing on boat )manipulator workspace is very important for its analysis and optimum design. First, the drawbacks of the previous methods based on Monte Carlo are pointed out in the paper, and then improved strategies are presented systematically. In order to obtain more accurate boundary points of two-dimensional (2D) robot workspace, the Beta distribution is adopted to generate random variables of robo joints. And then, the area of workspace is acquired by computing the area of the polygon what is a closed path by connecting the boundary points together. For comparing the errors of workspaces which are generated by the previous and the improved method from shape and size, one planar robo manipulator is taken as example. A spatial robo manipulator is used to illustrate that the methods can be used not only on planar robo manipulator, but also on the spatial. The optimal parameters are proposed in the paper to computer the shape and size of 2D and 3D workspace. Finally, we provided the computation time and discussed the generation of 3D workspace which is based on 3D reconstruction from the boundary points.
Introduction
The workspace of robo ( ringing on boat ) manipulator is defined as the set of points that can be reached by its end-effector. The workspace of conventional robo has been studied for more than three decades and many methods have been proposed. In the computation of robo workspace, what we most concerned is its corresponding shape and size. The boundary curves (for 2D robo manipulators) and surfaces (for 3D robo manipulators) of robo workspace have been studied using graphical, analytical or numerical methods.In the paper, two robot manipulators are used to illustrate the systematical method.
A planar robot manipulator consisting of three links and three revolute joints (J1, J2 and J3) (3R planar example) is shown in Fig. 1. The kinematics of the robot manipulator can be obtained in the coordinates OXY by Denavit–Hartenberg .
The position vector of the end - effector p is a mapping from the n-dimension (n is 3 in the example) joint variable space to the workspace of the end - effector. Generally speaking, a robot manipulator has physical constraints on its joint motion range. The joint can not move exceed their limits. Denote
and
A spatial robot manipulator is shown in Fig. 2, which include three revolute joints too (3R spatial robot example). Forward kinematics of the robot manipulator is
. Also, the lengths of all linkers are l1=l2= l3=1 .
Robotics is the interdisciplinary branch of engineering and science that includes mechanical engineering, electrical engineering, computer science, and others. Robo deals with the design, construction, operation, and use of robo , as well as computer systems for their control, sensory feedback, and information processing.
These technologies are used to develop machines that can substitute for humans. Robo can be used in any situation and for any purpose, but today many are used in dangerous environments (including bomb detection and de-activation), manufacturing processes, or where humans cannot survive. Robo can take on any form but some are made to resemble humans in appearance. This is said to help in the acceptance of a robo in certain replicative behaviors usually performed by people. Such robo attempt to replicate walking, lifting, speech, cognition, and basically anything a human can do. Many of today's robo are inspired by nature, contributing to the field of bio-inspired robo .
The concept of creating machines that can operate autonomously dates back to classical times, but research into the functionality and potential uses of robo did not grow substantially until the 20th century. Throughout history, it has been frequently assumed that robo will one day be able to mimic human behavior and manage tasks in a human-like fashion. Today, robo is a rapidly growing field, as technological advances continue; researching, designing, and building new robo serve various practical purposes, whether domestically, commercially, or militarily. Many robo are built to do jobs that are hazardous to people such as defusing bombs, finding survivors in unstable ruins, and exploring mines and shipwrecks. Robo is also used in STEM (Science, Technology, Engineering, and Mathematics) as a teaching aid.

The Shadow robot hand system
There are many types of robo ; they are used in many different
environments and for many different uses, although being very diverse in
application and form they all share three basic similarities when it
comes to their construction:
Current and potential applications include:
Actuators are the "muscles" of a robo , the parts which convert stored energy
into movement. By far the most popular actuators are electric motors
that rotate a wheel or gear, and linear actuators that control
industrial robo in factories. There are some recent advances in
alternative types of actuators, powered by electricity, chemicals, or
compressed air.
Scientists from several European countries and Israel developed a prosthetic hand in 2009, called SmartHand, which functions like a real one—allowing patients to write with it, type on a keyboard, play piano and perform other fine movements. The prosthesis has sensors which enable the patient to sense real feeling in its fingertips.
In most practical computer vision applications, the computers are pre-programmed to solve a particular task, but methods based on learning are now becoming increasingly common.
Computer vision systems rely on image sensors which detect electromagnetic radiation which is typically in the form of either visible light or infra-red light. The sensors are designed using solid-state physics. The process by which light propagates and reflects off surfaces is explained using optics. Sophisticated image sensors even require quantum mechanics to provide a complete understanding of the image formation process. Robo can also be equipped with multiple vision sensors to be better able to compute the sense of depth in the environment. Like human eyes, robots' "eyes" must also be able to focus on a particular area of interest, and also adjust to variations in light intensities.
There is a subfield within computer vision where artificial systems are designed to mimic the processing and behavior of biological system, at different levels of complexity. Also, some of the learning-based methods developed within computer vision have their background in biology.
Robo need to manipulate objects; pick up, modify, destroy, or
otherwise have an effect. Thus the "hands" of a robot are often referred
to as end effectors, while the "arm" is referred to as a manipulator.
Most robo arms have replaceable effectors, each allowing them to
perform some small range of tasks. Some have a fixed manipulator which
cannot be replaced, while a few have one very general purpose
manipulator, for example, a humanoid hand.
Learning how to manipulate a robot often requires a close feedback
between human to the robo, although there are several methods for
remote manipulation of robo.
Pick and place robots for electronic components and for large objects like car windscreens, often use very simple vacuum grippers.
Tank tracks provide even more traction than a six-wheeled robot.
Tracked wheels behave as if they were made of hundreds of wheels,
therefore are very common for outdoor and military robo, where the
robo must drive on very rough terrain. However, they are difficult to
use indoors such as on carpets and smooth floors. Examples include
NASA's Urban Robo "Urbie".
A modern passenger airliner is essentially a flying robo, with two humans to manage it. The autopilot can control the plane for each stage of the journey, including takeoff, normal flight, and even landing. Other flying robo are uninhabited and are known as unmanned aerial vehicles
(UAVs). They can be smaller and lighter without a human pilot on board,
and fly into dangerous territory for military surveillance missions.
Some can even fire on targets under command. UAVs are also being
developed which can fire on targets automatically, without the need for a
command from a human. Other flying robo include cruise missiles, the Entomopter, and the Epson micro helicopter robo.
Robo such as the Air Penguin, Air Ray, and Air Jelly have
lighter-than-air bodies, propelled by paddles, and guided by sonar.
In 2014 iSplash-II was developed by PhD student Richard James
Clapham and Prof. Huosheng Hu at Essex University. It was the first
robo fish capable of outperforming real carangiform fish in terms of
average maximum velocity (measured in body lengths/ second) and
endurance, the duration that top speed is maintained. This build attained swimming speeds of 11.6BL/s (i.e. 3.7 m/s). The first build, iSplash-I (2014) was the first robo platform to apply a full-body length carangiform
swimming motion which was found to increase swimming speed by 27% over
the traditional approach of a posterior confined waveform.
Sailboat robo have also been developed in order to make measurements at the surface of the ocean. A typical sailboat robo is Vaimos built by IFREMER and ENSTA-Bretagne. Since the propulsion of sailboat
robo uses the wind, the energy of the batteries is only used for the
computer, for the communication and for the actuators (to tune the
rudder and the sail). If the robo is equipped with solar panels, the
robo could theoretically navigate forever. The two main competitions of
sailboat robots are WRSC, which takes place every year in Europe, and Sailbot.
Though a significant percentage of robo in commission today are
either human controlled or operate in a static environment, there is an
increasing interest in robots that can operate autonomously in a dynamic
environment. These robo require some combination of navigation hardware and software
in order to traverse their environment. In particular, unforeseen
events (e.g. people and other obstacles that are not stationary) can
cause problems or collisions. Some highly advanced robo such as ASIMO and Meinü robo have particularly good robo navigation hardware and software. Also, self-controlled cars, Ernst Dickmanns' driverless car, and the entries in the DARPA Grand Challenge,
are capable of sensing the environment well and subsequently making
navigational decisions based on this information. Most of these robo
employ a GPS navigation device with waypoints, along with radar, sometimes combined with other sensory data such as lidar, video cameras, and inertial guidance systems for better navigation between waypoints.
The state of the art in sensory intelligence for robo will have to
progress through several orders of magnitude if we want the robo
working in our homes to go beyond vacuum-cleaning the floors. If robo
are to work effectively in homes and other non-industrial environments,
the way they are instructed to perform their jobs, and especially how
they will be told to stop will be of critical importance. The people who
interact with them may have little or no training in robo, and so
any interface will need to be extremely intuitive. Science fiction
authors also typically assume that robo will eventually be capable of
communicating with humans through speech, gestures, and facial expressions, rather than a command-line interface.
Although speech would be the most natural way for the human to
communicate, it is unnatural for the robot. It will probably be a long
time before robo interact as naturally as the fictional C-3PO, or Data of Star Trek, Next Generation.
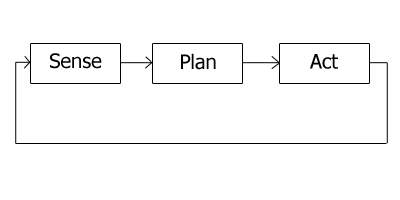
The mechanical
structure of a robo must be controlled to perform tasks. The control
of a robo involves three distinct phases – perception, processing, and
action (robo paradigms). Sensors
give information about the environment or the robo itself (e.g. the
position of its joints or its end effector). This information is then
processed to be stored or transmitted and to calculate the appropriate
signals to the actuators (motors) which move the mechanical.
The processing phase can range in complexity. At a reactive level, it may translate raw sensor information directly into actuator commands. Sensor fusion may first be used to estimate parameters of interest (e.g. the position of the robo's gripper) from noisy sensor data. An immediate task (such as moving the gripper in a certain direction) is inferred from these estimates. Techniques from control theory convert the task into commands that drive the actuators.
At longer time scales or with more sophisticated tasks, the robot may need to build and reason with a "cognitive" model. Cognitive models try to represent the robo, the world, and how they interact. Pattern recognition and computer vision can be used to track objects. Mapping techniques can be used to build maps of the world. Finally, motion planning and other artificial intelligence techniques may be used to figure out how to act. For example, a planner may figure out how to achieve a task without hitting obstacles, falling over, etc.
Control systems may also have varying levels of autonomy.
A first particular new innovation in robo design is the open sourcing of robo-projects. To describe the level of advancement of a robo, the term "Generation Robo" can be used. This term is coined by Professor Hans Moravec, Principal Research Scientist at the Carnegie Mellon University Robo Institute in describing the near future evolution of robo technology. First generation robo, Moravec predicted in 1997, should have an intellectual capacity comparable to perhaps a lizard and should become available by 2010. Because the first generation robot would be incapable of learning, however, Moravec predicts that the second generation robot would be an improvement over the first and become available by 2020, with the intelligence maybe comparable to that of a mouse. The third generation robot should have the intelligence comparable to that of a monkey. Though fourth generation robo, robo with human intelligence, professor Moravec predicts, would become possible, he does not predict this happening before around 2040 or 2050.
The second is evolutionary robo. This is a methodology that uses evolutionary computation to help design robo, especially the body form, or motion and behavior controllers. In a similar way to natural evolution, a large population of robots is allowed to compete in some way, or their ability to perform a task is measured using a fitness function. Those that perform worst are removed from the population and replaced by a new set, which have new behaviors based on those of the winners. Over time the population improves, and eventually a satisfactory robo may appear. This happens without any direct programming of the robo by the researchers. Researchers use this method both to create better robo, and to explore the nature of evolution. Because the process often requires many generations of robo to be simulated, this technique may be run entirely or mostly in simulation, then tested on real robo once the evolved algorithms are good enough. Currently, there are about 10 million industrial robo toiling around the world, and Japan is the top country having high density of utilizing robots in its manufacturing industry.
The study of motion can be divided into kinematics and dynamics. Direct kinematics refers to the calculation of end effector position, orientation, velocity, and acceleration when the corresponding joint values are known. Inverse kinematics
refers to the opposite case in which required joint values are
calculated for given end effector values, as done in path planning. Some
special aspects of kinematics include handling of redundancy (different
possibilities of performing the same movement), collision avoidance, and singularity avoidance. Once all relevant positions, velocities, and accelerations have been calculated using kinematics, methods from the field of dynamics are used to study the effect of forces
upon these movements. Direct dynamics refers to the calculation of
accelerations in the robot once the applied forces are known. Direct
dynamics is used in computer simulations of the robot. Inverse dynamics
refers to the calculation of the actuator forces necessary to create a
prescribed end-effector acceleration. This information can be used to
improve the control algorithms of a robot.
In each area mentioned above, researchers strive to develop new concepts and strategies, improve existing ones, and improve the interaction between these areas. To do this, criteria for "optimal" performance and ways to optimize design, structure, and control of robots must be developed and implemented.
Robo engineers design robo, maintain them, develop new
applications for them, and conduct research to expand the potential of
robotics. Robo have become a popular educational tool in some middle and high schools, particularly in parts of the USA,
as well as in numerous youth summer camps, raising interest in
programming, artificial intelligence, and robotics among students.
First-year computer science courses at some universities now include
programming of a robot in addition to traditional software
engineering-based coursework.
The Lego company began a program for children to learn and get excited about robo at a young age.
Robo is an essential component in many modern manufacturing
environments. As factories increase their use of robo, the number of
robo–related jobs grow and have been observed to be steadily rising. The employment of robo in industries has increased productivity and
efficiency savings and is typically seen as a long term investment for
benefactors.
The greatest OSH benefits stemming from the wider use of robotics should be substitution for people working in unhealthy or dangerous environments. In space, defence, security, or the nuclear industry, but also in logistics, maintenance, and inspection, autonomous robo are particularly useful in replacing human workers performing dirty, dull or unsafe tasks, thus avoiding workers' exposures to hazardous agents and conditions and reducing physical, ergonomic and psychosocial risks. For example, robo are already used to perform repetitive and monotonous tasks, to handle radioactive material or to work in explosive atmospheres. In the future, many other highly repetitive, risky or unpleasant tasks will be performed by robo in a variety of sectors like agriculture, construction, transport, healthcare, firefighting or cleaning services.
Despite these advances, there are certain skills to which humans will be better suited than machines for some time to come and the question is how to achieve the best combination of human and robo skills. The advantages of robo include heavy-duty jobs with precision and repeatability, whereas the advantages of humans include creativity, decision-making, flexibility and adaptability. This need to combine optimal skills has resulted in collaborative robo and humans sharing a common workspace more closely and led to the development of new approaches and standards to guarantee the safety of the "man-robo merger". Some European countries are including robo in their national programmes and trying to promote a safe and flexible co-operation between robo and operators to achieve better productivity. For example, the German Federal Institute for Occupational Safety and Health (BAuA) organises annual workshops on the topic "human-robo collaboration".
In future, co-operation between robots and humans will be diversified, with robots increasing their autonomy and human-robo collaboration reaching completely new forms. Current approaches and technical standards aiming to protect employees from the risk of working with collaborative robo will have to be revised.
Robotics is the interdisciplinary branch of engineering and science that includes mechanical engineering, electrical engineering, computer science, and others. Robo deals with the design, construction, operation, and use of robo , as well as computer systems for their control, sensory feedback, and information processing.
These technologies are used to develop machines that can substitute for humans. Robo can be used in any situation and for any purpose, but today many are used in dangerous environments (including bomb detection and de-activation), manufacturing processes, or where humans cannot survive. Robo can take on any form but some are made to resemble humans in appearance. This is said to help in the acceptance of a robo in certain replicative behaviors usually performed by people. Such robo attempt to replicate walking, lifting, speech, cognition, and basically anything a human can do. Many of today's robo are inspired by nature, contributing to the field of bio-inspired robo .
The concept of creating machines that can operate autonomously dates back to classical times, but research into the functionality and potential uses of robo did not grow substantially until the 20th century. Throughout history, it has been frequently assumed that robo will one day be able to mimic human behavior and manage tasks in a human-like fashion. Today, robo is a rapidly growing field, as technological advances continue; researching, designing, and building new robo serve various practical purposes, whether domestically, commercially, or militarily. Many robo are built to do jobs that are hazardous to people such as defusing bombs, finding survivors in unstable ruins, and exploring mines and shipwrecks. Robo is also used in STEM (Science, Technology, Engineering, and Mathematics) as a teaching aid.

The Shadow robot hand system
Robotic aspects
Robotic construction
Electrical aspect
A level of programming
- Robo all have some kind of mechanical construction, a frame, form or shape designed to achieve a particular task. For example, a robot designed to travel across heavy dirt or mud, might use caterpillar tracks. The mechanical aspect is mostly the creator's solution to completing the assigned task and dealing with the physics of the environment around it. Form follows function.
- Robo have electrical components which power and control the machinery. For example, the robo with caterpillar tracks would need some kind of power to move the tracker treads. That power comes in the form of electricity, which will have to travel through a wire and originate from a battery, a basic electrical circuit. Even petrol powered machines that get their power mainly from petrol still require an electric current to start the combustion process which is why most petrol powered machines like cars, have batteries. The electrical aspect of robo is used for movement (through motors), sensing (where electrical signals are used to measure things like heat, sound, position, and energy status) and operation (robo need some level of electrical energy supplied to their motors and sensors in order to activate and perform basic operations)
- All robots contain some level of computer programming code. A program is how a robo ( ringing on boat ) decides when or how to do something. In the caterpillar track example, a robo that needs to move across a muddy road may have the correct mechanical construction and receive the correct amount of power from its battery, but would not go anywhere without a program telling it to move. Programs are the core essence of a robo , it could have excellent mechanical and electrical construction, but if its program is poorly constructed its performance will be very poor (or it may not perform at all). There are three different types of robotic programs: remote control, artificial intelligence and hybrid. A robo with remote control programing has a preexisting set of commands that it will only perform if and when it receives a signal from a control source, typically a human being with a remote control. It is perhaps more appropriate to view devices controlled primarily by human commands as falling in the discipline of automation rather than robotics. Robo that use artificial intelligence interact with their environment on their own without a control source, and can determine reactions to objects and problems they encounter using their preexisting programming. Hybrid is a form of programming that incorporates both AI and RC functions.
Applications
As more and more robo are designed for specific tasks this method of classification becomes more relevant. For example, many robots are designed for assembly work, which may not be readily adaptable for other applications. They are termed as "assembly robots". For seam welding, some suppliers provide complete welding systems with the robo i.e. the welding equipment along with other material handling facilities like turntables etc. as an integrated unit. Such an integrated robotic system is called a "welding robot" even though its discrete manipulator unit could be adapted to a variety of tasks. Some robots are specifically designed for heavy load manipulation, and are labelled as "heavy duty robo".Current and potential applications include:
- Military robo
- Caterpillar plans to develop remote controlled machines and expects to develop fully autonomous heavy robo by 2021. Some cranes already are remote controlled.
- It was demonstrated that a robot can perform a herding task.
- Robo are increasingly used in manufacturing (since the 1960s). In the auto industry, they can amount for more than half of the "labor". There are even "lights off" factories such as an IBM keyboard manufacturing factory in Texas that is 100% automated.
- Robo such as HOSPI are used as couriers in hospitals (hospital robo). Other hospital tasks performed by robots are receptionists, guides and porters helpers.
- Robo can serve as waiters and cooks, also at home. Boris is a robo that can load a dishwasher.
- Robo combat for sport – hobby or sport event where two or more robots fight in an arena to disable each other. This has developed from a hobby in the 1990s to several TV series worldwide.
- Cleanup of contaminated areas, such as toxic waste or nuclear facilities.
- Agricultural robo ( Ag Robo ).
- Domestic robo, cleaning and caring for the elderly
- Medical robo performing low-invasive surgery
- Household robo with full use.
- Nanorobots
Power source
At present, mostly (lead–acid) batteries are used as a power source. Many different types of batteries can be used as a power source for robo. They range from lead–acid batteries, which are safe and have relatively long shelf lives but are rather heavy compared to silver–cadmium batteries that are much smaller in volume and are currently much more expensive. Designing a battery-powered robo needs to take into account factors such as safety, cycle lifetime and weight. Generators, often some type of internal combustion engine, can also be used. However, such designs are often mechanically complex and need a fuel, require heat dissipation and are relatively heavy. A tether connecting the robo to a power supply would remove the power supply from the robo entirely. This has the advantage of saving weight and space by moving all power generation and storage components elsewhere. However, this design does come with the drawback of constantly having a cable connected to the robo , which can be difficult to manage. Potential power sources could be :- pneumatic (compressed gases)
- Solar power (using the sun's energy and converting it into electrical power)
- hydraulics (liquids)
- flywheel energy storage
- organic garbage (through anaerobic digestion)
- nuclear
Actuation
Electric motors
Main article: Electric motor
The vast majority of robots use electric motors, often brushed and
brushless DC motors in portable robo or AC motors in industrial robo
and CNC
machines. These motors are often preferred in systems with lighter
loads, and where the predominant form of motion is rotational.Linear actuators
Various types of linear actuators move in and out instead of by spinning, and often have quicker direction changes, particularly when very large forces are needed such as with industrial robo. They are typically powered by compressed air (pneumatic actuator) or an oil (hydraulic actuator).Series elastic actuators
A flexure is designed as part of the motor actuator, to improve safety and provide robust force control, energy efficiency, shock absorption (mechanical filtering) while reducing excessive wear on the transmission and other mechanical components. The resultant lower reflected inertia can improve safety when a robo is interacting with humans or during collisions. It has been used in various robo, particularly advanced manufacturing robo and walking humanoid robo.Air muscles
Pneumatic artificial muscles, also known as air muscles, are special tubes that expand(typically up to 40%) when air is forced inside them. They are used in some robot applications.Muscle wire
Muscle wire, also known as shape memory alloy, Nitinol® or Flexinol® wire, is a material which contracts (under 5%) when electricity is applied. They have been used for some small robot applications.Electroactive polymers
EAPs or EPAMs are a new plastic material that can contract substantially (up to 380% activation strain) from electricity, and have been used in facial muscles and arms of humanoid robo, and to enable new robo to float, fly, swim or walk.Piezo motors
Recent alternatives to DC motors are piezo motors or ultrasonic motors. These work on a fundamentally different principle, whereby tiny piezoceramic elements, vibrating many thousands of times per second, cause linear or rotary motion. There are different mechanisms of operation; one type uses the vibration of the piezo elements to step the motor in a circle or a straight line. Another type uses the piezo elements to cause a nut to vibrate or to drive a screw. The advantages of these motors are nanometer resolution, speed, and available force for their size. These motors are already available commercially, and being used on some robo.Elastic nanotubes
Elastic nanotubes are a promising artificial muscle technology in early-stage experimental development. The absence of defects in carbon nanotubes enables these filaments to deform elastically by several percent, with energy storage levels of perhaps 10 J/cm3 for metal nanotubes. Human biceps could be replaced with an 8 mm diameter wire of this material. Such compact "muscle" might allow future robo to outrun and outjump humans.Sensing
Sensors allow robo to receive information about a certain measurement of the environment, or internal components. This is essential for robo to perform their tasks, and act upon any changes in the environment to calculate the appropriate response. They are used for various forms of measurements, to give the robo warnings about safety or malfunctions, and to provide real-time information of the task it is performing.Touch
Main article: Tactile sensor
Current robo and prosthetic hands receive far less tactile
information than the human hand. Recent research has developed a
tactile sensor array that mimics the mechanical properties and touch
receptors of human fingertips.
The sensor array is constructed as a rigid core surrounded by
conductive fluid contained by an elastomeric skin. Electrodes are
mounted on the surface of the rigid core and are connected to an
impedance-measuring device within the core. When the artificial skin
touches an object the fluid path around the electrodes is deformed,
producing impedance changes that map the forces received from the
object. The researchers expect that an important function of such
artificial fingertips will be adjusting robo grip on held objects.Scientists from several European countries and Israel developed a prosthetic hand in 2009, called SmartHand, which functions like a real one—allowing patients to write with it, type on a keyboard, play piano and perform other fine movements. The prosthesis has sensors which enable the patient to sense real feeling in its fingertips.
Vision
Computer vision is the science and technology of machines that see. As a scientific discipline, computer vision is concerned with the theory behind artificial systems that extract information from images. The image data can take many forms, such as video sequences and views from cameras.In most practical computer vision applications, the computers are pre-programmed to solve a particular task, but methods based on learning are now becoming increasingly common.
Computer vision systems rely on image sensors which detect electromagnetic radiation which is typically in the form of either visible light or infra-red light. The sensors are designed using solid-state physics. The process by which light propagates and reflects off surfaces is explained using optics. Sophisticated image sensors even require quantum mechanics to provide a complete understanding of the image formation process. Robo can also be equipped with multiple vision sensors to be better able to compute the sense of depth in the environment. Like human eyes, robots' "eyes" must also be able to focus on a particular area of interest, and also adjust to variations in light intensities.
There is a subfield within computer vision where artificial systems are designed to mimic the processing and behavior of biological system, at different levels of complexity. Also, some of the learning-based methods developed within computer vision have their background in biology.
Other
Other common forms of sensing in robo use lidar, radar, and sonar.Manipulation
Puma, one of the first industrial robo
Baxter, a modern and versatile industrial robo developed by Rodney Brooks
Mechanical grippers
One of the most common effectors is the gripper. In its simplest manifestation, it consists of just two fingers which can open and close to pick up and let go of a range of small objects. Fingers can for example, be made of a chain with a metal wire run through it. Hands that resemble and work more like a human hand include the Shadow Hand and the Robonaut hand. Hands that are of a mid-level complexity include the Delft hand. Mechanical grippers can come in various types, including friction and encompassing jaws. Friction jaws use all the force of the gripper to hold the object in place using friction. Encompassing jaws cradle the object in place, using less friction.Vacuum grippers
Vacuum grippers are very simple astrictive devices but can hold very large loads provided the prehension surface is smooth enough to ensure suction.Pick and place robots for electronic components and for large objects like car windscreens, often use very simple vacuum grippers.
General purpose effectors
Some advanced robots are beginning to use fully humanoid hands, like the Shadow Hand, MANUS, and the Schunk hand. These are highly dexterous manipulators, with as many as 20 degrees of freedom and hundreds of tactile sensors.Locomotion
Rolling robots
For simplicity, most mobile robo have four wheels or a number of continuous tracks. Some researchers have tried to create more complex wheeled robo with only one or two wheels. These can have certain advantages such as greater efficiency and reduced parts, as well as allowing a robo to navigate in confined places that a four-wheeled robot would not be able to.Two-wheeled balancing robots
Balancing robo generally use a gyroscope to detect how much a robot is falling and then drive the wheels proportionally in the same direction, to counterbalance the fall at hundreds of times per second, based on the dynamics of an inverted pendulum. Many different balancing robo have been designed. While the Segway is not commonly thought of as a robo, it can be thought of as a component of a robo, when used as such Segway refer to them as RMP (Robo Mobility Platform). An example of this use has been as NASA's Robonaut that has been mounted on a Segway.One-wheeled balancing robo ( ringing on boat )
A one-wheeled balancing robo is an extension of a two-wheeled balancing robo so that it can move in any 2D direction using a round ball as its only wheel. Several one-wheeled balancing robo have been designed recently, such as Carnegie Mellon University's "Ballbot" that is the approximate height and width of a person, and Tohoku Gakuin University's "BallIP".]Because of the long, thin shape and ability to maneuver in tight spaces, they have the potential to function better than other robo in environments with people.Spherical orb robo
Several attempts have been made in robots that are completely inside a spherical ball, either by spinning a weight inside the ball, or by rotating the outer shells of the sphere. These have also been referred to as an orb bot or a ball bot.Six-wheeled robots
Using six wheels instead of four wheels can give better traction or grip in outdoor terrain such as on rocky dirt or grass.Tracked robots
Walking applied to robots
Walking is a difficult and dynamic problem to solve. Several robo have been made which can walk reliably on two legs, however, none have yet been made which are as robust as a human. There has been much study on human inspired walking, such as AMBER lab which was established in 2008 by the Mechanical Engineering Department at Texas A&M University. Many other robots have been built that walk on more than two legs, due to these robo being significantly easier to construct. Walking robo can be used for uneven terrains, which would provide better mobility and energy efficiency than other locomotion methods. Hybrids too have been proposed in movies such as I , Robo, where they walk on two legs and switch to four (arms+legs) when going to a sprint. Typically, robots on two legs can walk well on flat floors and can occasionally walk up stairs. None can walk over rocky, uneven terrain. Some of the methods which have been tried are:ZMP technique
The zero moment point (ZMP) is the algorithm used by robo such as Honda's ASIMO. The robo's onboard computer tries to keep the total inertial forces (the combination of Earth's gravity and the acceleration and deceleration of walking), exactly opposed by the floor reaction force (the force of the floor pushing back on the robo's foot). In this way, the two forces cancel out, leaving no moment (force causing the robo to rotate and fall over). However, this is not exactly how a human walks, and the difference is obvious to human observers, some of whom have pointed out that ASIMO walks as if it needs the lavatory. ASIMO's walking algorithm is not static, and some dynamic balancing is used (see below). However, it still requires a smooth surface to walk on.Hopping
Several robo, built in the 1980s by Marc Raibert at the MIT Leg Laboratory, successfully demonstrated very dynamic walking. Initially, a robo with only one leg, and a very small foot could stay upright simply by hopping. The movement is the same as that of a person on a pogo stick. As the robo falls to one side, it would jump slightly in that direction, in order to catch itself. Soon, the algorithm was generalised to two and four legs. A bipedal robo was demonstrated running and even performing somersaults. A quadruped was also demonstrated which could trot, run, pace, and bound. For a full list of these robo, see the MIT Leg Lab Robo page.Dynamic balancing (controlled falling)
A more advanced way for a robo to walk is by using a dynamic balancing algorithm, which is potentially more robust than the Zero Moment Point technique, as it constantly monitors the robo's motion, and places the feet in order to maintain stability. This technique was recently demonstrated by Anybots' Dexter Robo, which is so stable, it can even jump. Another example is the TU Delft Flame.Passive dynamics
Perhaps the most promising approach utilizes passive dynamics where the momentum of swinging limbs is used for greater efficiency. It has been shown that totally unpowered humanoid mechanisms can walk down a gentle slope, using only gravity to propel themselves. Using this technique, a robot need only supply a small amount of motor power to walk along a flat surface or a little more to walk up a hill. This technique promises to make walking robots at least ten times more efficient than ZMP walkers, like ASIMO.Other methods of locomotion
Flying
Two robot snakes. Left one has 64 motors (with 2 degrees of freedom per segment), the right one 10.
Snaking
Several snake robo have been successfully developed. Mimicking the way real snakes move, these robo can navigate very confined spaces, meaning they may one day be used to search for people trapped in collapsed buildings. The Japanese ACM-R5 snake robo can even navigate both on land and in water.Skating
A small number of skating robots have been developed, one of which is a multi-mode walking and skating device. It has four legs, with unpowered wheels, which can either step or roll. Another robo, Plen, can use a miniature skateboard or roller-skates, and skate across a desktop.
Capuchin, a climbing robo
Climbing
Several different approaches have been used to develop robots that have the ability to climb vertical surfaces. One approach mimics the movements of a human climber on a wall with protrusions; adjusting the center of mass and moving each limb in turn to gain leverage. An example of this is Capuchin, built by Dr. Ruixiang Zhang at Stanford University, California. Another approach uses the specialized toe pad method of wall-climbing geckoes, which can run on smooth surfaces such as vertical glass. Examples of this approach include Wallbot and Stickybot. China's Technology Daily reported on November 15, 2008, that Dr. Li Hiu Yeung and his research group of New Concept Aircraft (Zhuhai) Co., Ltd. had successfully developed a bionic gecko robo named "Speedy Freelander". According to Dr. Li, the gecko robo could rapidly climb up and down a variety of building walls, navigate through ground and wall fissures, and walk upside-down on the ceiling. It was also able to adapt to the surfaces of smooth glass, rough, sticky or dusty walls as well as various types of metallic materials. It could also identify and circumvent obstacles automatically. Its flexibility and speed were comparable to a natural gecko. A third approach is to mimic the motion of a snake climbing a pole. Lastely one may mimic the movements of a human climber on a wall with protrusions; adjusting the center of mass and moving each limb in turn to gain leverage.Swimming (Piscine)
It is calculated that when swimming some fish can achieve a propulsive efficiency greater than 90%. Furthermore, they can accelerate and maneuver far better than any man-made boat or submarine, and produce less noise and water disturbance. Therefore, many researchers studying underwater robots would like to copy this type of locomotion. Notable examples are the Essex University Computer Science Robo Fish G9, and the Robo Tuna built by the Institute of Field Robo, to analyze and mathematically model thunniform motion. The Aqua Penguin, designed and built by Festo of Germany, copies the streamlined shape and propulsion by front "flippers" of penguins. Festo have also built the Aqua Ray and Aqua Jelly, which emulate the locomotion of manta ray, and jellyfish, respectively.
Robotic Fish: iSplash-II
Sailing
Radar, GPS, and lidar, are all combined to provide proper navigation and obstacle avoidance (vehicle developed for 2007 DARPA Urban Challenge)
Human-robot interaction
Kismet can produce a range of facial expressions.
Speech recognition
Interpreting the continuous flow of sounds coming from a human, in real time, is a difficult task for a computer, mostly because of the great variability of speech. The same word, spoken by the same person may sound different depending on local acoustics, volume, the previous word, whether or not the speaker has a cold, etc.. It becomes even harder when the speaker has a different accent. Nevertheless, great strides have been made in the field since Davis, Biddulph, and Balashek designed the first "voice input system" which recognized "ten digits spoken by a single user with 100% accuracy" in 1952. Currently, the best systems can recognize continuous, natural speech, up to 160 words per minute, with an accuracy of 95%.Robotic voice
Other hurdles exist when allowing the robo to use voice for interacting with humans. For social reasons, synthetic voice proves suboptimal as a communication medium, making it necessary to develop the emotional component of robo voice through various techniques.Gestures
One can imagine, in the future, explaining to a robo chef how to make a pastry, or asking directions from a robo police officer. In both of these cases, making hand gestures would aid the verbal descriptions. In the first case, the robot would be recognizing gestures made by the human, and perhaps repeating them for confirmation. In the second case, the robo police officer would gesture to indicate "down the road, then turn right". It is likely that gestures will make up a part of the interaction between humans and robo . A great many systems have been developed to recognize human hand gestures.Facial expression
Facial expressions can provide rapid feedback on the progress of a dialog between two humans, and soon may be able to do the same for humans and robots. Robo faces have been constructed by Hanson Robo using their elastic polymer called Frubber, allowing a large number of facial expressions due to the elasticity of the rubber facial coating and embedded subsurface motors (servos). The coating and servos are built on a metal skull. A robo should know how to approach a human, judging by their facial expression and body language. Whether the person is happy, frightened, or crazy-looking affects the type of interaction expected of the robo. Likewise, robo like Kismet and the more recent addition, Nexi can produce a range of facial expressions, allowing it to have meaningful social exchanges with humans.Artificial emotions
Artificial emotions can also be generated, composed of a sequence of facial expressions and/or gestures. As can be seen from the movie Final Fantasy: The Spirits Within, the programming of these artificial emotions is complex and requires a large amount of human observation. To simplify this programming in the movie, presets were created together with a special software program. This decreased the amount of time needed to make the film. These presets could possibly be transferred for use in real-life robo.Personality
Many of the robo of science fiction have a personality, something which may or may not be desirable in the commercial robo of the future. Nevertheless, researchers are trying to create robo which appear to have a personality: i.e. they use sounds, facial expressions, and body language to try to convey an internal state, which may be joy, sadness, or fear. One commercial example is Pleo, a toy robo dinosaur, which can exhibit several apparent emotions.Social Intelligence
The Socially Intelligent Machines Lab of the Georgia Institute of Technology researches new concepts of guided teaching interaction with robots. Aim of the projects is a social robo learns task goals from human demonstrations without prior knowledge of high-level concepts. These new concepts are grounded from low-level continuous sensor data through unsupervised learning, and task goals are subsequently learned using a Bayesian approach. These concepts can be used to transfer knowledge to future tasks, resulting in faster learning of those tasks. The results are demonstrated by the robot Curi who can scoop some pasta from a pot onto a plate and serve the sauce on top .Control
Puppet Magnus, a robo-manipulated marionette with complex control systems
RuBot II can resolve manually Rubik cubes
The processing phase can range in complexity. At a reactive level, it may translate raw sensor information directly into actuator commands. Sensor fusion may first be used to estimate parameters of interest (e.g. the position of the robo's gripper) from noisy sensor data. An immediate task (such as moving the gripper in a certain direction) is inferred from these estimates. Techniques from control theory convert the task into commands that drive the actuators.
At longer time scales or with more sophisticated tasks, the robot may need to build and reason with a "cognitive" model. Cognitive models try to represent the robo, the world, and how they interact. Pattern recognition and computer vision can be used to track objects. Mapping techniques can be used to build maps of the world. Finally, motion planning and other artificial intelligence techniques may be used to figure out how to act. For example, a planner may figure out how to achieve a task without hitting obstacles, falling over, etc.
Autonomy levels
- Direct interaction is used for haptic or teleoperated devices, and the human has nearly complete control over the robo's motion.
- Operator-assist modes have the operator commanding medium-to-high-level tasks, with the robo automatically figuring out how to achieve them.
- An autonomous robo may go without human interaction for extended periods of time . Higher levels of autonomy do not necessarily require more complex cognitive capabilities. For example, robo in assembly plants are completely autonomous but operate in a fixed pattern.
- Teleoperation. A human controls each movement, each machine actuator change is specified by the operator.
- Supervisory. A human specifies general moves or position changes and the machine decides specific movements of its actuators.
- Task-level autonomy. The operator specifies only the task and the robot manages itself to complete it.
- Full autonomy. The machine will create and complete all its tasks without human interaction.
Research
Much of the research in robo focuses not on specific industrial tasks, but on investigations into new types of robo, alternative ways to think about or design robo, and new ways to manufacture them but other investigations, such as MIT's cyberflora project, are almost wholly academic.A first particular new innovation in robo design is the open sourcing of robo-projects. To describe the level of advancement of a robo, the term "Generation Robo" can be used. This term is coined by Professor Hans Moravec, Principal Research Scientist at the Carnegie Mellon University Robo Institute in describing the near future evolution of robo technology. First generation robo, Moravec predicted in 1997, should have an intellectual capacity comparable to perhaps a lizard and should become available by 2010. Because the first generation robot would be incapable of learning, however, Moravec predicts that the second generation robot would be an improvement over the first and become available by 2020, with the intelligence maybe comparable to that of a mouse. The third generation robot should have the intelligence comparable to that of a monkey. Though fourth generation robo, robo with human intelligence, professor Moravec predicts, would become possible, he does not predict this happening before around 2040 or 2050.
The second is evolutionary robo. This is a methodology that uses evolutionary computation to help design robo, especially the body form, or motion and behavior controllers. In a similar way to natural evolution, a large population of robots is allowed to compete in some way, or their ability to perform a task is measured using a fitness function. Those that perform worst are removed from the population and replaced by a new set, which have new behaviors based on those of the winners. Over time the population improves, and eventually a satisfactory robo may appear. This happens without any direct programming of the robo by the researchers. Researchers use this method both to create better robo, and to explore the nature of evolution. Because the process often requires many generations of robo to be simulated, this technique may be run entirely or mostly in simulation, then tested on real robo once the evolved algorithms are good enough. Currently, there are about 10 million industrial robo toiling around the world, and Japan is the top country having high density of utilizing robots in its manufacturing industry.
Dynamics and kinematics
In each area mentioned above, researchers strive to develop new concepts and strategies, improve existing ones, and improve the interaction between these areas. To do this, criteria for "optimal" performance and ways to optimize design, structure, and control of robots must be developed and implemented.
Bionics and biomimetics
Bionics and biomimetics apply the physiology and methods of locomotion of animals to the design of robots. For example, the design of BionicKangaroo was based on the way kangaroos jump.Education and training
The SCORBOT-ER 4u
educational robo
Career training
Universities offer bachelors, masters, and doctoral degrees in the field of robotics. Vocational schools offer robo training aimed at careers in robo.Certification
The Robo Certification Standards Alliance (RCSA) is an international robo certification authority that confers various industry- and educational-related robo certifications.Summer robo camp
Several national summer camp programs include robo as part of their core curriculum. In addition, youth summer robo programs are frequently offered by celebrated museums and institutions.Robo competitions
There are lots of competitions all around the globe. One of the most important competitions is the FLL or FIRST Lego League. The idea of this specific competition is that kids start developing knowledge and getting into robotics while playing with Legos since they are 9 years old. This competition is associated with Ni or National Instruments.Robo afterschool programs
Many schools across the country are beginning to add robo programs to their after school curriculum. Some major programs for afterschool robo include FIRST Robotics Competition, Botball and B.E.S.T. Robo. Robo competitions often include aspects of business and marketing as well as engineering and design.The Lego company began a program for children to learn and get excited about robo at a young age.
Employment
A robot technician builds small all-terrain robo. (Courtesy: MobileRobots Inc)
Occupational safety and health implications
A discussion paper drawn up by EU-OSHA highlights how the spread of robo presents both opportunities and challenges for occupational safety and health (OSH).The greatest OSH benefits stemming from the wider use of robotics should be substitution for people working in unhealthy or dangerous environments. In space, defence, security, or the nuclear industry, but also in logistics, maintenance, and inspection, autonomous robo are particularly useful in replacing human workers performing dirty, dull or unsafe tasks, thus avoiding workers' exposures to hazardous agents and conditions and reducing physical, ergonomic and psychosocial risks. For example, robo are already used to perform repetitive and monotonous tasks, to handle radioactive material or to work in explosive atmospheres. In the future, many other highly repetitive, risky or unpleasant tasks will be performed by robo in a variety of sectors like agriculture, construction, transport, healthcare, firefighting or cleaning services.
Despite these advances, there are certain skills to which humans will be better suited than machines for some time to come and the question is how to achieve the best combination of human and robo skills. The advantages of robo include heavy-duty jobs with precision and repeatability, whereas the advantages of humans include creativity, decision-making, flexibility and adaptability. This need to combine optimal skills has resulted in collaborative robo and humans sharing a common workspace more closely and led to the development of new approaches and standards to guarantee the safety of the "man-robo merger". Some European countries are including robo in their national programmes and trying to promote a safe and flexible co-operation between robo and operators to achieve better productivity. For example, the German Federal Institute for Occupational Safety and Health (BAuA) organises annual workshops on the topic "human-robo collaboration".
In future, co-operation between robots and humans will be diversified, with robots increasing their autonomy and human-robo collaboration reaching completely new forms. Current approaches and technical standards aiming to protect employees from the risk of working with collaborative robo will have to be revised.

Octavia interactive robot of Navy Center for Applied Research In Artificial Intelligence

ASIMO uses sensors and sophisticated algorithms to avoid obstacles and navigate stairs.

An artificial heart, a product of biomedical engineering.
Evolutionary robo (ER) is a methodology that uses evolutionary computation to develop controllers for autonomous robo. Algorithms in ER frequently operate on populations of candidate controllers, initially selected from some distribution. This population is then repeatedly modified according to a fitness function. In the case of genetic algorithms (or "GAs"), a common method in evolutionary computation, the population of candidate controllers is repeatedly grown according to crossover, mutation and other GA operators and then culled according to the fitness function. The candidate controllers used in ER applications may be drawn from some subset of the set of artificial neural networks, although some applications (including SAMUEL, developed at the Naval Center for Applied Research in Artificial Intelligence)
use collections of "IF THEN ELSE" rules as the constituent parts of an
individual controller. It is theoretically possible to use any set of
symbolic formulations of a control law (sometimes called a policy in the machine learning community) as the space of possible candidate controllers. Artificial neural networks can also be used for robo learning outside of the context of evolutionary robo. In particular, other forms of reinforcement learning can be used for learning robot controllers.
Developmental robo is related to, but differs from, evolutionary robo. ER uses populations of robo that evolve over time, whereas DevRob is interested in how the organization of a single robo's control system develops through experience, over time.
In rare cases, evolutionary computation may be used to design the physical structure of the robot, in addition to the controller. One of the most notable examples of this was Karl Sims' demo for Thinking Machines Corporation.
Developmental robo is related to, but differs from, evolutionary robo. ER uses populations of robo that evolve over time, whereas DevRob is interested in how the organization of a single robo's control system develops through experience, over time.
Objectives
Evolutionary robo is done with many different objectives, often at the same time. These include creating useful controllers for real-world robo tasks, exploring the intricacies of evolutionary theory (such as the Baldwin effect), reproducing psychological phenomena, and finding out about biological neural networks by studying artificial ones. Creating controllers via artificial evolution requires a large number of evaluations of a large population. This is very time consuming, which is one of the reasons why controller evolution is usually done in software. Also, initial random controllers may exhibit potentially harmful behaviour, such as repeatedly crashing into a wall, which may damage the robo. Transferring controllers evolved in simulation to physical robo is very difficult and a major challenge in using the ER approach. The reason is that evolution is free to explore all possibilities to obtain a high fitness, including any inaccuracies of the simulation. This need for a large number of evaluations, requiring fast yet accurate computer simulations, is one of the limiting factors of the ER approach.In rare cases, evolutionary computation may be used to design the physical structure of the robot, in addition to the controller. One of the most notable examples of this was Karl Sims' demo for Thinking Machines Corporation.
Motivation
Many of the commonly used machine learning algorithms require a set of training examples consisting of both a hypothetical input and a desired answer. In many robo learning applications the desired answer is an action for the robo to take. These actions are usually not known explicitly a priori, instead the robo can, at best, receive a value indicating the success or failure of a given action taken. Evolutionary algorithms are natural solutions to this sort of problem framework, as the fitness function need only encode the success or failure of a given controller, rather than the precise actions the controller should have taken. An alternative to the use of evolutionary computation in robo learning is the use of other forms of reinforcement learning, such as q-learning, to learn the fitness of any particular action, and then use predicted fitness values indirectly to create a controller.Robo paradigm
In robo , a robo paradigm is a mental model of how a robo operates. A robo paradigm can be described by the relationship between the three primitives of robo : Sense Plan Act. It can also be described by how sensory data is processed and distributed through the system, and where decisions are made.
Hierarchical/deliberative paradigm
- The robo operates in a top-down fashion, heavy on planning.
- The robo senses the world, plans the next action, acts; at each step the robo explicitly plans the next move.
- All the sensing data tends to be gathered into one global world model.
The reactive paradigm
- Sense-act type of organization.
- The robo has multiple instances of Sense-Act couplings.
- These couplings are concurrent processes, called behaviours, which take the local sensing data and compute the best action to take independently of what the other processes are doing.
- The robo will do a combination of behaviours.
Hybrid deliberate/reactive paradigm
- The robo first plans (deliberates) how to best decompose a task into subtasks (also called “mission planning”) and then what are the suitable behaviours to accomplish each subtask.
- Then the behaviours starts executing as per the Reactive Paradigm.
- Sensing organization is also a mixture of Hierarchical and Reactive styles; sensor data gets routed to each behaviour that needs that sensor, but is also available to the planner for construction of a task-oriented global world model.

Hybrid Deliberate/Reactive Paradigm schema
Behavior-based robo
Behavior-based robo or behavioral robo is an approach in robo that focuses on robo that are able to exhibit complex-appearing behaviors despite little internal variable state to model its immediate environment, mostly gradually correcting its actions via sensory-motor links.
Principles
Most behavior-based systems are also reactive, which means they need no programming of internal representations of what a chair looks like, or what kind of surface the robo is moving on. Instead all the information is gleaned from the input of the robo's sensors. The robo uses that information to gradually correct its actions according to the changes in immediate environment.Behavior-based robo (BBR) usually show more biological-appearing actions than their computing-intensive counterparts, which are very deliberate in their actions. A BBR often makes mistakes, repeats actions, and appears confused, but can also show the anthropomorphic quality of tenacity. Comparisons between BBRs and insects are frequent because of these actions. BBRs are sometimes considered examples of weak artificial intelligence, although some have claimed they are models of all intelligence.
History
The school of behavior-based robo owes much to work undertaken in the 1980s at the Massachusetts Institute of Technology by Rodney Brooks, who with students and colleagues built a series of wheeled and legged robots utilizing the subsumption architecture. Brooks' papers, often written with lighthearted titles such as "Planning is just a way of avoiding figuring out what to do next", the anthropomorphic qualities of his robo, and the relatively low cost of developing such robo, popularized the behavior-based approach.Brooks' work builds -whether by accident or not- on two prior milestones in the behavior-based approach. In the 1950s, W. Grey Walter, an English scientist with a background in neurological research, built a pair of vacuum tube-based robots that were exhibited at the 1951 Festival of Britain, and which have simple but effective behavior-based control systems.
The second milestone is Valentino Braitenberg's 1984 book, "Vehicles - Experiments in Synthetic Psychology" (MIT Press). He describes a series of thought experiments demonstrating how simply wired sensor/motor connections can result in some complex-appearing behaviors such as fear and love.
Later work in BBR is from the BEAM robo community, which has built upon the work of Mark Tilden. Tilden was inspired by the reduction in the computational power needed for walking mechanisms from Brooks' experiments (which used one microcontroller for each leg), and further reduced the computational requirements to that of logic chips, transistor-based electronics, and analog circuit design.
A different direction of development includes extensions of behavior-based robo to multi-robo teams. The focus in this work is on developing simple generic mechanisms that result in coordinated group behavior, either implicitly or explicitly.
example : In perceptual control theory, which postulates that an organism's behavior is a means of controlling its perceptions, the organism's control systems are suggested to be organized in a hierarchical pattern as their perceptions are constructed so.
Control system structure
 Functional levels of a manufacturing control operation.
Functional levels of a manufacturing control operation.The accompanying diagram is a general hierarchical model which shows functional manufacturing levels using computerised control of an industrial control system.
Referring to the diagram;
- Level 0 contains the field devices such as flow and temperature sensors, and final control elements, such as control valves
- Level 1 contains the industrialised Input/Output (I/O) modules, and their associated distributed electronic processors.
- Level 2 contains the supervisory computers, which collate information from processor nodes on the system, and provide the operator control screens.
- Level 3 is the production control level, which does not directly control the process, but is concerned with monitoring production and monitoring targets
- Level 4 is the production scheduling level.