proof of Pythagoras calculation in dynamic function robot

Pythagorean theorem reads in a right-angled triangle the hypotenuse squared same applies to the number of squares of the other sides. In general, if the triangle ABC is right-angled in C then the Pythagorean theorem can be stated AB ^ 2 = AC + BC ^ 2 ^ 2.
The Pythagorean Theorem is a very famous theorem. This theorem will be used in calculating the broad flat wake. Besides being used in the calculation of the flat wake, calculations in 3 dimensions or the other will also often use the Pythagorean theorem. Many books write this theorem as c ^ 2 = a ^ 2 + b ^ 2. Where c is the hypotenuse.
Proof of this theorem is very diverse. Very many ways to prove Pythagoras's theorem. Here will be given some proof of the Pythagorean theorem. From the very basic evidence until proof is quite complicated. Most evidence of the Pythagorean theorem is the development of core evidence (evidence base). 


I. The first evidence :


Supplied four right-angled triangles. Look at the picture above. 4 triangles above are similar triangles. Have the sides a, b and c. and side c is the hypotenuse of the triangle. The third triangle side are the result of the rotation of 90, 180 and 270 degrees of the first triangle.
The area of each triangle is \ frac {ab} {2}. So spacious 4 triangles are 2ab.
The triangles be set so that membentung square with side c as shown below. 




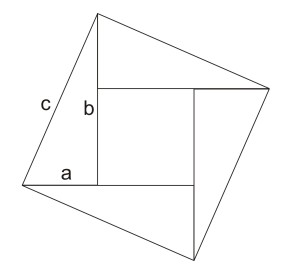
Note the image of the arrangement 4 the triangle. The images form a square with sides c. and in it there is a small square. The long side of the small square is (b-a).
Directly we can determine the extent of the huge square, ie c ^ 2. And indirectly, a large square area with side c is equal to the area of 4 triangles plus a small square area having a side (b-a). Thus obtained,

c ^ 2 = 2ab + (b-a) ^ 2
c ^ 2 = 2ab + b ^ a ^ 2 + 2-2ab
c ^ 2 = b ^ 2 + a ^ 2   


II. the second proof  




 Note the picture. The picture is a picture of 2 square. Large square is a square that has a side length, and a small square has a side length that is b.
Large square area that certainly is a ^ 2. And a small square area is b ^ 2. So spacious wake above is b ^ 2 + a ^ 2  




Both the square we combine. And we created a line so that as in the picture. C side becomes the hypotenuse of the triangle. then we cut into triangles. and we move it to the top and right side as shown below.


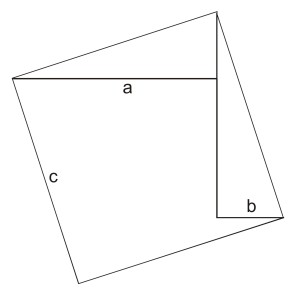
Square area with a side c of the course is c ^ 2. Because the two square at the outset is equal to one large square with sides c above, then certainly an area of 2 square equal to the area's first large square with the c side.
thus, c ^ 2 = b ^ 2 + a ^ 2

III. The third proof  



The picture is a picture of a trapezoid made up of three triangles. The spacious trapezoid is \ frac {1} {2} (a + b) (a + b). searched using the trapezoidal area formula. That is half multiplied by the number of times the high side of the parallel trapezoid. Seek broad flat wake above can also use an extensive number of triangles (see picture). that is

\ Frac {1} {2} ab + \ frac {1} {2} ab + \ frac {1} {2} c ^ 2.

Size counts is fixed. Namely the trapezium shape. so it should be both widely sought by the different steps that should be the same. Retrieved,

\ Frac {1} {2} (a + b) (a + b) = \ frac {1} {2} ab + \ frac {1} {2} ab + \ frac {1} {2} c ^ 2
\ Frac {1} {2} (a ^ 2 + 2ab + b ^ 2) = ab + \ frac {1} {2} c ^ 2
\ Frac {1} {2} a ^ 2 + ab + \ frac {1} {2} b ^ 2 = ab + \ frac {1} {2} c ^ 2
a ^ 2 + b ^ 2 = c ^ 2  


MACAM-MACAM BILANGAN TRIPEL PYTHAGORAS

1. (3,4,5)
2. (5,12,13)
3. (7,24,25)
4. (8,15,17)
5. (9,40,41)
6. (11,60,61)
7. (12,35,37)
8. (13,84,85)
9. (15,112,113)
10. (16,63,65)
11. (17,144,145)
12. (19,180,181)
13. (20,21,29)
14. (20,99,101)
15. (21,220,221)
16. (23,264,265)
17. (24,143,145)
18. (25,312,313)
19. (27,364,365)
20. (28,45,53)
21. (28,195,197)
22. (29,420,421)
23. (31,480,481)
24. (32,255,257)
25. (33,56,65)
26. (33,544,545)
27. (35,612,613)
28. (36,77,85)
29. (36,323,325)
30. (37,684,685)
31. (39,80,89)
32. (39,760,761)
33. (40,399,401)
34. (41,840,841)
35. (43,924,925)
36. (44,117,125)
37. (44,483,485)
38. (48,55,73)
39. (48,575,577)
40. (51,140,149)
41. (52,165,173)
42. (52,675,677)
43. (56,783,785)
44. (57,176,185)
45. (60,91,109)
46. (60,221,229)
47. (60,899,901)
48. (65,72,97)
49. (68,285,293)
50. (69,260,269)
51. (75,308,317)
52. (76,357,365)
53. (84,187,205)
54. (84,437,445)
55. (85,132,157)
56. (87,416,425)
57. (88,105,137)
58. (92,525,533)
59. (93,476,485)
60. (95,168,193)
61. (96,247,265)
62. (100,621,629)
63. (104,153,185)
64. (105,208,233)
65. (105,608,617)
66. (108,725,733)
67. (111,680,689)
68. (115,252,277)
69. (116,837,845)
70. (119,120,169)
71. (120,209,241)
72. (120,391,409)
73. (123,836,845)
74. (124,957,965)
75. (129,920,929)
76. (132,475,493)
77. (133,156,205)
78. (135,352,377)
79. (136,273,305)
80. (140,171,221)
81. (145,408,433)
82. (152,345,377)
83. (155,468,493)
84. (156,667,685)
85. (160,231,281)
86. (161,240,289)
87. (165,532,557)
88. (168,425,457)
89. (168,775,793)
90. (175,288,337)
91. (180,299,349)
92. (184,513,545)
93. (185,672,697)
94. (189,340,389)
95. (195,748,773)
96. (200,609,641)
97. (203,396,445)
98. (204,253,325)
99. (205,828,853)
100. (207,224,305)
101. (215,912,937)
102. (216,713,745)
103. (217,456,505)
104. (220,459,509)
105. (225,272,353)
106. (228,325,397)
107. (231,520,569)
108. (232,825,857)
109. (240,551,601)
110. (248,945,977)
111. (252,275,373)
112. (259,660,709)
113. (260,651,701)
114. (261,380,461)
115. (273,736,785)
116. (276,493,565)
117. (279,440,521)
118. (280,351,449)
119. (280,759,809)
120. (287,816,865)
121. (297,304,425)
122. (300,589,661)
123. (301,900,949)
124. (308,435,533)
125. (315,572,653)
126. (319,360,481)
127. (333,644,725)
128. (336,377,505)
129. (336,527,625)
130. (341,420,541)
131. (348,805,877)
132. (364,627,725)
133. (368,465,593)
134. (369,800,881)
135. (372,925,997)
136. (385,552,673)
137. (387,884,965)
138. (396,403,565)
139. (400,561,689)
140. (407,624,745)
141. (420,851,949)
142. (429,460,629)
143. (429,700,821)
144. (432,665,793)
145. (451,780,901)
146. (455,528,697)
147. (464,777,905)
148. (468,595,757)
149. (473,864,985)
150. (481,600,769)
151. (504,703,865)
152. (533,756,925)
153. (540,629,829)
154. (555,572,797)
155. (580,741,941)
156. (615,728,953)
157. (616,663,905) 

Pythagoras theory to determine the position of robot 

at the moment of making a robot with a special feature heavily dependent according to the needs. One of the sensors used in robots are the rotary encoder
Rotary encoder: a digital sensor used to detect displacement or movement of the robot. Along with the development of robots, FPGA development shows a positive response, so scientists began trying to apply it to the world of robots. One example application is to determine the position of the robot. calculating the position of the robot with FPGA using the rotary encoder.
FPGA (Field Programmable Gate Array) that is programmable major device that is composed of independent logic modules that can be configured through the canals of programmable routing. FPGA is a type IC HDL (Hardware Description Language).

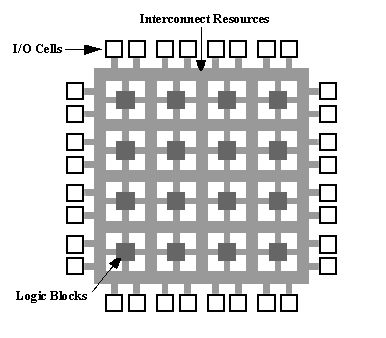
In general, the inner architecture of FPGA IC consists
on three main elements, namely Input / Output Block (IOB), Configurable Logic Block (CLB) and programmable interconnect. Input Output Blocks (IOB), as an interface between the external and internal pins of the device use rlogic .Configure Logic Blocks (CLB), part of which will process all forms of logic circuit and Programmable Interconnect, the part that connects the CLB CLB one with the other
















B. Rotary encoder
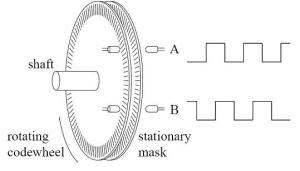
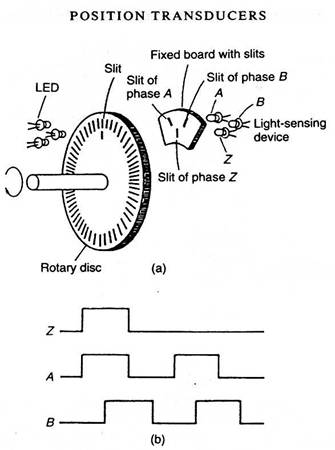
Rotary encoder is an electromechanical device that can monitor the movement and position. Rotary encoder generally uses optical sensors to produce a series of pulses which translates into motion, position, and direction. So that the angular position of a shaft rotating object can be processed into information in the form of digital code by a rotary encoder
Rotary encoder
composed of a thin disk that has holes in the circular disk. LED is placed on one side of the disc so that
the light will be heading to the disc. On the other hand, a photo-transistor is placed so that the photo-transistor can detect light from the LED opposite. When the position of the disk results in light of the LED can achieve photo-transistor through the existing holes, then the photo-transistor will experience saturation and will produce a square wave pulse. The more the pulse train generated in one round determines
The accuracy rotary encoder.

       





    








A. System Block Diagram
Block diagram of the system, manually controlled robot (driven), resulting in the movement, rotary encoder, serves to detect the movement. The resulting output rotary encoder
   1, rotary encoder
    2, and a rotary encoder
    3 in the form of pulses that represent the position of the x-axis (x), and the movement of the x-axis angle (θ). De2 by FPGA output data respectively
rotary encoder is processed to be calculated movement of each rotary encoder then proceeds in the form of a position (x, y) is displayed on the LCD


     




   

     




         


B. Determine the position (x, y) robot

Pythagorean theorem
Round rotary encoder used as a reference as position
the x-axis robot, when the robot walks then it will
generating robot movement angle to the axis x (θ). So with the known position of the x-axis and the angle thetanya, then the position of the y-axis robot can be known by using the Pythagorean theorem. Here is a triangle theorem of Pythagoras.   

Rotary encoder adalah divais elektromekanik yang dapat memonitor gerakan dan posisi. Rotary encoder umumnya menggunakan sensor optik untuk menghasilkan serial pulsa yang dapat diartikan menjadi gerakan, posisi, dan arah. Sehingga posisi sudut suatu poros benda berputar dapat diolah menjadi informasi berupa kode digital oleh rotary encoder untuk diteruskan oleh rangkaian kendali. Rotary encoder umumnya digunakan pada pengendalian robot, motor drive, dsb.

Rotary encoder tersusun dari suatu piringan tipis yang memiliki lubang-lubang pada bagian lingkaran piringan. LED ditempatkan pada salah satu sisi piringan sehingga cahaya akan menuju ke piringan. Di sisi yang lain suatu photo-transistor diletakkan sehingga photo-transistor ini dapat mendeteksi cahaya dari LED yang berseberangan. Piringan tipis tadi dikopel dengan poros motor, atau divais berputar lainnya yang ingin kita ketahui posisinya, sehingga ketika motor berputar piringan juga akan ikut berputar. Apabila posisi piringan mengakibatkan cahaya dari LED dapat mencapai photo-transistor melalui lubang-lubang yang ada, maka photo-transistor akan mengalami saturasi dan akan menghasilkan suatu pulsa gelombang persegi. Gambar 1 menunjukkan bagan skematik sederhana dari rotary encoder. Semakin banyak deretan pulsa yang dihasilkan pada satu putaran menentukan akurasi rotary encoder tersebut, akibatnya semakin banyak jumlah lubang yang dapat dibuat pada piringan menentukan akurasi rotary encoder tersebut.

Gambar 1. Blok penyusun rotary encoder

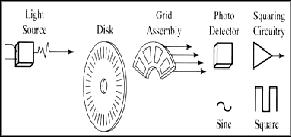
Rangkaian penghasil pulsa (Gambar 2) yang digunakan umumnya memiliki output yang berubah dari +5V menjadi 0.5V ketika cahaya diblok oleh piringan dan ketika diteruskan ke photo-transistor. Karena divais ini umumnya bekerja dekat dengan motor DC maka banyak noise yang timbul sehingga biasanya output akan dimasukkan ke low-pass filter dahulu. Apabila low-pass filter digunakan, frekuensi cut-off yang dipakai umumnya ditentukan oleh jumlah slot yang ada pada piringan dan seberapa cepat piringan tersebut berputar, dinyatakan dengan:

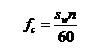(1)

Dimana f_c adalah frekuensi cut-off filter, s_w adalah kecepatan piringan dan n adalah jumlah slot pada piringan.

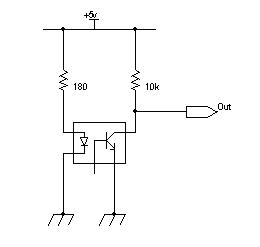Gambar 2. Rangkaian tipikal penghasil pulsa pada rotary encoder

Terdapat dua jenis rotary encoder yang digunakan, Absolute rotary encoder dan incremental rotary encoder. Masing-masing rotary encoder ini akan dipaparkan pada bagian berikutnya.

ABSOLUTE ROTARY ENCODER

Absolute encoder menggunakan piringan dan sinyal optik yang diatur sedemikian sehingga dapat menghasilkan kode digital untuk menyatakan sejumlah posisi tertentu dari poros yang dihubungkan padanya. Piringan yang digunakan untuk absolut encoder tersusun dari segmen-segmen cincin konsentris yang dimulai dari bagian tengah piringan ke arah tepi luar piringan yang jumlah segmennya selalu dua kali jumlah segmen cincin sebelumnya. Cincin pertama di bagian paling dalam memiliki satu segmen transparan dan satu segmen gelap, cincin kedua memiliki dua segmen transparan dan dua segmen gelap, dan seterusnya hingga cincin terluar. Sebagai contoh apabila absolut encoder memiliki 16 cincin konsentris maka cincin terluarnya akan memiliki 32767 segmen. Gambar 3 menunjukkan pola cincin pada piringan absolut encoder yang memiliki 16 cincin.

Gambar 3. Contoh susunan pola 16 cincin konsentris pada absolut encoder

Karena setiap cincin pada piringan absolute encoder memiliki jumlah segmen kelipatan dua dari cincin sebelumnya, maka susunan ini akan membentuk suatu sistem biner. Untuk menghasilkan sistem biner pada susunan cincin maka diperlukan pasangan LED dan photo-transistor sebanyak jumlah cincin yang ada pada absolut encoder tersebut.

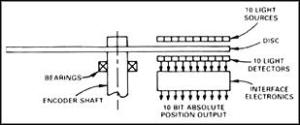Gambar 4. Contoh piringan dengan 10 cincin dan 10 LED – photo-transistor untuk membentuk sistem biner 10 bit.

Sistem biner yang untuk menginterpretasi posisi yang diberikan oleh absolute encoder dapat menggunakan kode gray atau kode biner biasa, tergantung dari pola cincin yang digunakan. Untuk lebih jelas, kita lihat contoh absolut encoder yang hanya tersusun dari 4 buah cincin untuk membentuk kode 4 bit. Apabila encoder ini dihubungkan pada poros, maka photo-transistor akan mengeluarkan sinyal persegi sesuai dengan susunan cincin yang digunakan. Gambar 5 dan 6 menunjukkan contoh perbedaan diagram keluaran untuk absolute encoder tipe gray code dan tipe binary code.

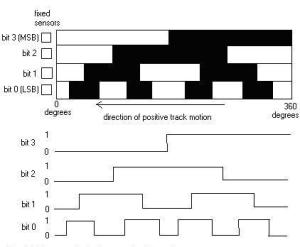
Gambar 5. Contoh diagram keluaran absolut encoder 4-bit tipe gray code

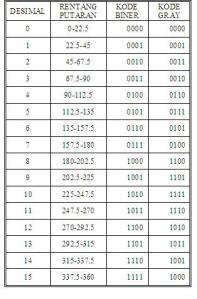
Dengan absolute encoder 4-bit ini maka kita akan mendapatkan 16 informasi posisi yang berbeda yang masing-masing dinyatakan dengan kode biner atau kode gray tertentu. Tabel 1 menyatakan posisi dan output biner yang bersesuaian untuk absolut encoder 4-bit. Dengan membaca output biner yang dihasilkan maka posisi dari poros yang kita ukur dapat kita ketahui untuk diteruskan ke rangkaian pengendali. Semakin banyak bit yang kita pakai maka posisi yang dapat kita peroleh akan semakin banyak.

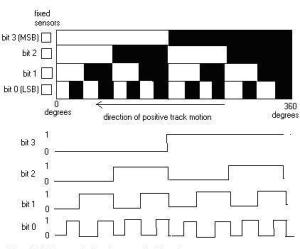
Gambar 6. Contoh diagram keluaran absolut encoder 4-bit tipe binary code

Tabel 1. Output biner dan posisi yang bersesuaian pada absolute encoder 4-bit

INCREMENTAL ROTARY ENCODER

Incremental encoder terdiri dari dua track atau single track dan dua sensor yang disebut channel A dan B (Gambar 7). Ketika poros berputar, deretan pulsa akan muncul di masing-masing channel pada frekuensi yang proporsional dengan kecepatan putar sedangkan hubungan fasa antara channel A dan B menghasilkan arah putaran. Dengan menghitung jumlah pulsa yang terjadi terhadap resolusi piringan maka putaran dapat diukur. Untuk mengetahui arah putaran, dengan mengetahui channel mana yang leading terhadap channel satunya dapat kita tentukan arah putaran yang terjadi karena kedua channel tersebut akan selalu berbeda fasa seperempat putaran (quadrature signal). Seringkali terdapat output channel ketiga, disebut INDEX, yang menghasilkan satu pulsa per putaran berguna untuk menghitung jumlah putaran yang terjadi.

Gambar 7. susunan piringan untuk incremental encoder

Contoh pola diagram keluaran dari suatu incremental encoder ditunjukkan pada Gambar 8. Resolusi keluaran dari sinyal quadrature A dan B dapat dibuat beberapa macam, yaitu 1X, 2X dan 4X. Resolusi 1X hanya memberikan pulsa tunggal untuk setiap siklus salah satu sinya A atau B, sedangkan resolusi 4X memberikan pulsa setiap transisi pada kedua sinyal A dan B menjadi empat kali resolusi 1X. Arah putaran dapat ditentukan melalui level salah satu sinyal selama transisi terhadap sinyal yang kedua. Pada contoh resolusi 1X, A = arah bawah dengan B = 1 menunjukkan arah putaran searah jarum jam, sebaliknya B = arah bawah dengan A = 1 menunjukkan arah berlawanan jarum jam.

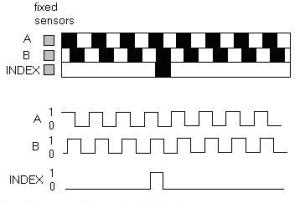
Gambar 8. Contoh pola keluaran incremental encoder

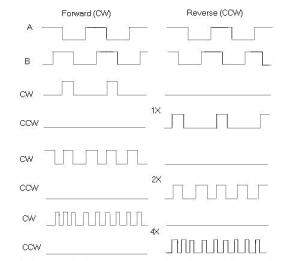
Gambar 9. output dan arah putaran pada resolusi yang berbeda-beda

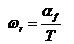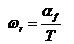Pada incremental encoder, beberapa cara dapat digunakan untuk menentukan kecepatan yang diamati dari sinyal pulsa yang dihasilkan. Diantaranya adalah menggunakan frequencymeter dan periodimeter.

Cara yang sederhana untuk menentukan kecepatan dapat dengan frequencymeter, yakni menghitung jumlah pulsa dari encoder, n, pada selang waktu yang tetap, T, yang merupakan periode loop kecepatan (Gambar 10). Apabila α adalah sudut antara pulsa encoder, maka sudut putaran pada suatu periode adalah:

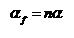(2)

Sehingga kecepatan putar akan kita dapatkan sebagai:

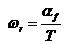(3)

Kelemahan yang muncul pada cara ini adalah pada setiap periode sudut α_f yang didapat merupakan kelipatan integer dari α. Ini akan dapat menghasilkan quantification error pada kecepatan yang ingin diukur.

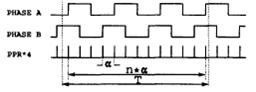
Gambar 10. Sinyal keluaran encoder untuk pengukuran kecepatan dengan frequencymeter

Cara yang lain adalah dengan menggunakan periodimeter. Dengan cara ini kita akan mengukur kecepatan tidak lagi dengan menghitung jumlah pulsa encoder tetapi dengan menghitung clock frekuensi tinggi (HF Clock) untuk sebuah pulsa dari encoder yaitu mengukur periode pulsa dari encoder (Gambar 11). Apabila α_p adalah sudut dari pulsa encoder, t adalah periode dari HF clock, dan n adalah jumlah pulsa HF yang terhitung pada counter. Maka waktu untuk sebuah pulsa encoder, T_p,  adalah:

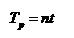
(4)

Sehingga kecepatan yang akan kita ukur dapat kita peroleh dengan:

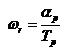
(5)

Seperti halnya pada frequencymeter, disini juga muncul quantification error karena waktu T_p akan selalu merupakan perkalian integer dengan t.

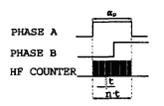Gambar 11. Pengukuran kecepatan dengan menggunakan Periodimeter