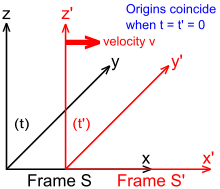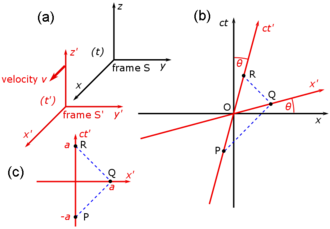
The Ellipse in Space

Thanks to My Wife - Thanks to My Parents - Thanks to My Child MARJESLO SAN
El_Lip_Se
__________________________________________________________________________________In mathematics, an ellipse is a plane curve surrounding two focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. As such, it generalizes a circle, which is the special type of ellipse in which the two focal points are the same. The elongation of an ellipse is measured by its eccentricity e, a number ranging from e = 0 (the limiting case of a circle) to e = 1 (the limiting case of infinite elongation, no longer an ellipse but a parabola).
Analytically, the equation of a standard ellipse centered at the origin with width 2a and height 2b is:
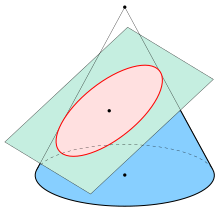
An ellipse (red) obtained as the intersection of a cone with an inclined plane.
An ellipse may also be defined in terms of one focal point and a line outside the ellipse called the directrix: for all points on the ellipse, the ratio between the distance to the focus and the distance to the directrix is a constant. This constant ratio is the above-mentioned eccentricity:
- .

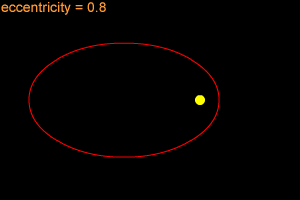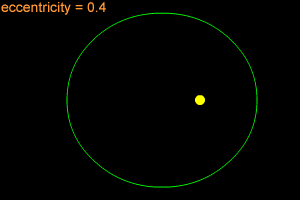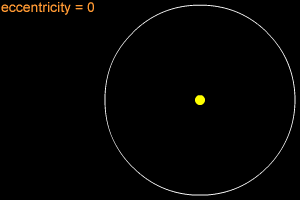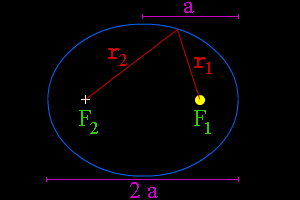
Ellipse: notations

Ellipses: examples with increasing eccentricity
Definition as locus of points
Ellipse: definition by sum of distances to foci
Ellipse: definition by focus and circular directrix
- Given two fixed points called the foci and a distance which is greater than the distance between the foci, the ellipse is the set of points such that the sum of the distances is equal to :
The case yields a circle and is included as a special type of ellipse.
The equation can be viewed in a different way (see figure):
- If is the circle with midpoint and radius , then the distance of a point to the circle equals the distance to the focus :
Using Dandelin spheres, one can prove that any plane section of a cone with a plane is an ellipse, assuming the plane does not contain the apex and has slope less than that of the lines on the cone.
In Cartesian coordinates
Shape parameters:
- a: semi-major axis,
- b: semi-minor axis,
- c: linear eccentricity,
- p: semi-latus rectum (usually ).
Standard equation
The standard form of an ellipse in Cartesian coordinates assumes that the origin is the center of the ellipse, the x-axis is the major axis, and:- the foci are the points ,
- the vertices are .
It follows from the equation that the ellipse is symmetric with respect to the coordinate axes and hence with respect to the origin.
Parameters
Semi-major and semi-minor axes a ≥ b
Throughout this article is the semi-major axis, i.e. In general the canonical ellipse equation may have (and hence the ellipse would be taller than it is wide); in this form the semi-major axis would be . This form can be converted to the standard form by transposing the variable names and and the parameter names andLinear eccentricity c
This is the distance from the center to a focus: .Eccentricity e
The eccentricity can be expressed as:- ,
Semi-latus rectum l
The length of the chord through one of the foci, perpendicular to the major axis, is called the latus rectum. One half of it is the semi-latus rectum . A calculation shows:Tangent
An arbitrary line intersects an ellipse at 0, 1, or 2 points, respectively called an exterior line, tangent and secant. Through any point of an ellipse there is a unique tangent. The tangent at a point of the ellipse has the coordinate equation:- with
- There are then cases:
- Then line and the ellipse have only point in common, and is a tangent. The tangent direction has perpendicular vector , so the tangent line has equation for some . Because is on the tangent and the ellipse, one obtains .
- Then line has a second point in common with the ellipse, and is a secant.
If and are two points of the ellipse such that , then the points lie on two conjugate diameters (see below). (If , the ellipse is a circle and "conjugate" means "orthogonal".)
Shifted ellipse
If the standard ellipse is shifted to have center , its equation isGeneral ellipse
In analytic geometry, the ellipse is defined as a quadric: the set of points of the Cartesian plane that, in non-degenerate cases, satisfy the implicit equationTo distinguish the degenerate cases from the non-degenerate case, let ∆ be the determinant
The general equation's coefficients can be obtained from known semi-major axis , semi-minor axis , center coordinates , and rotation angle (the angle from the positive horizontal axis to the ellipse's major axis) using the formulae:
Parametric representation
The construction of points based on the parametric equation and the interpretation of parameter t, which is due to de la Hire
Ellipse points calculated by the rational representation with equal spaced parameters ().
Standard parametric representation
Using trigonometric functions, a parametric representation of the standard ellipse is:Rational representation
With the substitution and trigonometric formulae one obtainsFor this formula represents the right upper quarter of the ellipse moving counter-clockwise with increasing The left vertex is the limit
Rational representations of conic sections are commonly used in Computer Aided Design
Tangent slope as parameter
A parametric representation, which uses the slope of the tangent at a point of the ellipse can be obtained from the derivative of the standard representation :The equation of the tangent at point has the form . The still unknown can be determined by inserting the coordinates of the corresponding ellipse point :
General ellipse
Ellipse as an affine image of the unit circle
- Any ellipse is an affine image of the unit circle with equation .
- parametric representation
- vertices
- implicit representation
- .
- ellipse in space
Polar forms
Polar form relative to center
Polar coordinates centered at the center.
Polar form relative to focus
Polar coordinates centered at focus.
In the slightly more general case of an ellipse with one focus at the origin and the other focus at angular coordinate , the polar form is
Eccentricity and the directrix property
Ellipse: directrix property
- For an arbitrary point
of the ellipse, the quotient of the distance to one focus and to the
corresponding directrix (see diagram) is equal to the eccentricity:
The converse is also true and can be used to define an ellipse (in a manner similar to the definition of a parabola):
- For any point (focus), any line (directrix) not through , and any real number with the ellipse is the locus of points for which the quotient of the distances to the point and to the line is that is:
(The choice yields a parabola, and if , a hyperbola.)
Pencil of conics with a common vertex and common semi-latus rectum
- Proof
- and
If , introduce new parameters so that , and then the equation above becomes
- General ellipse
Focus-to-focus reflection property
Ellipse: the tangent bisects the supplementary angle of the angle between the lines to the foci.
Rays from one focus reflect off the ellipse to pass through the other focus.
- The normal at a point bisects the angle between the lines .
- Proof
Let be the point on the line with the distance to the focus , is the semi-major axis of the ellipse. Let line be the bisector of the supplementary angle to the angle between the lines . In order to prove that is the tangent line at point , one checks that any point on line which is different from cannot be on the ellipse. Hence has only point in common with the ellipse and is, therefore, the tangent at point .
From the diagram and the triangle inequality one recognizes that holds, which means: . But if is a point of the ellipse, the sum should be .
- Application
Drawing ellipses
Central projection of circles (gate)
If there is no ellipsograph available, one can draw an ellipse using an approximation by the four osculating circles at the vertices.
For any method described below
- the knowledge of the axes and the semi-axes is necessary (or equivalent: the foci and the semi-major axis).
- Ellipse construction: paper strip method 1
Ellipse construction: paper strip method 2
- Method 2
- a strip of paper of length .
This method is the base for several ellipsographs (see section below).
Similar to the variation of the paper strip method 1 a variation of the paper strip method 2 can be established (see diagram) by cutting the part between the axes into halves.
- Trammel of Archimedes (principle)
- Ellipsograph due to Benjamin Bramer
As hypotrochoid
An ellipse (in red) as a special case of the hypotrochoid with R = 2r
As plane sections of quadrics
Ellipses appear as plane sections of the following quadrics:- Ellipsoid
- Elliptic cone
- Elliptic cylinder
- Hyperboloid of one sheet
- Hyperboloid of two sheets
Applications
Physics
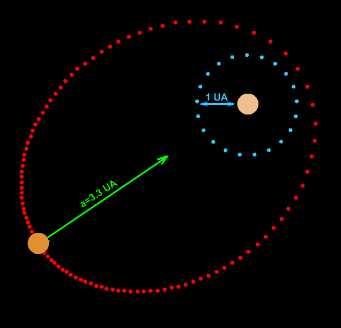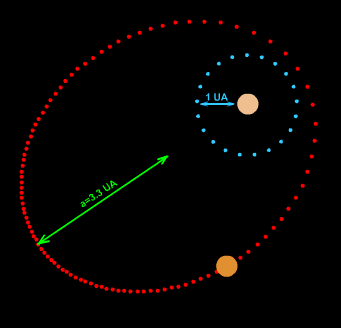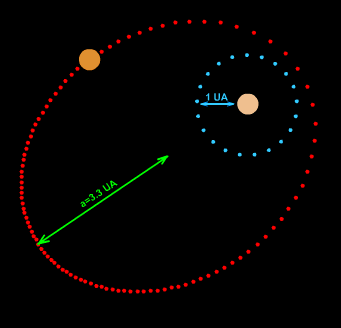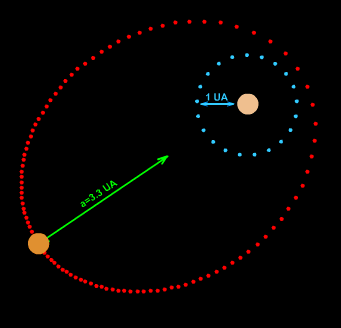
Planetary orbits
In the 17th century, Johannes Kepler discovered that the orbits along which the planets travel around the Sun are ellipses with the Sun [approximately] at one focus, in his first law of planetary motion. Later, Isaac Newton explained this as a corollary of his law of universal gravitation.More generally, in the gravitational two-body problem, if the two bodies are bound to each other (that is, the total energy is negative), their orbits are similar ellipses with the common barycenter being one of the foci of each ellipse. The other focus of either ellipse has no known physical significance. The orbit of either body in the reference frame of the other is also an ellipse, with the other body at the same focus.
Keplerian elliptical orbits are the result of any radially directed attraction force whose strength is inversely proportional to the square of the distance. Thus, in principle, the motion of two oppositely charged particles in empty space would also be an ellipse. (However, this conclusion ignores losses due to electromagnetic radiation and quantum effects, which become significant when the particles are moving at high speed.)
For elliptical orbits, useful relations involving the eccentricity are:
- is the radius at apoapsis (the farthest distance)
- is the radius at periapsis (the closest distance)
- is the length of the semi-major axis
- .
Harmonic oscillators
The general solution for a harmonic oscillator in two or more dimensions is also an ellipse. Such is the case, for instance, of a long pendulum that is free to move in two dimensions; of a mass attached to a fixed point by a perfectly elastic spring; or of any object that moves under influence of an attractive force that is directly proportional to its distance from a fixed attractor. Unlike Keplerian orbits, however, these "harmonic orbits" have the center of attraction at the geometric center of the ellipse, and have fairly simple equations of motion.Phase visualization
In electronics, the relative phase of two sinusoidal signals can be compared by feeding them to the vertical and horizontal inputs of an oscilloscope. If the Lissajous figure display is an ellipse, rather than a straight line, the two signals are out of phase.Elliptical gears
Two non-circular gears with the same elliptical outline, each pivoting around one focus and positioned at the proper angle, turn smoothly while maintaining contact at all times. Alternatively, they can be connected by a link chain or timing belt, or in the case of a bicycle the main chainring may be elliptical, or an ovoid similar to an ellipse in form. Such elliptical gears may be used in mechanical equipment to produce variable angular speed or torque from a constant rotation of the driving axle, or in the case of a bicycle to allow a varying crank rotation speed with inversely varying mechanical advantage.Elliptical bicycle gears make it easier for the chain to slide off the cog when changing gears.
An example gear application would be a device that winds thread onto a conical bobbin on a spinning machine. The bobbin would need to wind faster when the thread is near the apex than when it is near the base.
Optics
- In a material that is optically anisotropic (birefringent), the refractive index depends on the direction of the light. The dependency can be described by an index ellipsoid. (If the material is optically isotropic, this ellipsoid is a sphere.)
- In lamp-pumped solid-state lasers, elliptical cylinder-shaped reflectors have been used to direct light from the pump lamp (coaxial with one ellipse focal axis) to the active medium rod (coaxial with the second focal axis).[19]
- In laser-plasma produced EUV light sources used in microchip lithography, EUV light is generated by plasma positioned in the primary focus of an ellipsoid mirror and is collected in the secondary focus at the input of the lithography machine.
Statistics and finance
In statistics, a bivariate random vector (X, Y) is jointly elliptically distributed if its iso-density contours—loci of equal values of the density function—are ellipses. The concept extends to an arbitrary number of elements of the random vector, in which case in general the iso-density contours are ellipsoids. A special case is the multivariate normal distribution. The elliptical distributions are important in finance because if rates of return on assets are jointly elliptically distributed then all portfolios can be characterized completely by their mean and variance—that is, any two portfolios with identical mean and variance of portfolio return have identical distributions of portfolio return.Computer graphics
Drawing an ellipse as a graphics primitive is common in standard display libraries, such as the MacIntosh QuickDraw API, and Direct2D on Windows. Jack Bresenham at IBM is most famous for the invention of 2D drawing primitives, including line and circle drawing, using only fast integer operations such as addition and branch on carry bit. M. L. V. Pitteway extended Bresenham's algorithm for lines to conics in 1967. Another efficient generalization to draw ellipses was invented in 1984 by Jerry Van Aken.In 1970 Danny Cohen presented at the "Computer Graphics 1970" conference in England a linear algorithm for drawing ellipses and circles. In 1971, L. B. Smith published similar algorithms for all conic sections and proved them to have good properties. These algorithms need only a few multiplications and additions to calculate each vector.
It is beneficial to use a parametric formulation in computer graphics because the density of points is greatest where there is the most curvature. Thus, the change in slope between each successive point is small, reducing the apparent "jaggedness" of the approximation.
- Drawing with Bézier paths
Optimization theory
It is sometimes useful to find the minimum bounding ellipse on a set of points. The ellipsoid method is quite useful for attacking this problem.________________________________________________________________________________
MACH ( Moving Audio Combine Humanoid )
Mach number
In fluid dynamics, the Mach number is a dimensionless quantity representing the ratio of flow velocity past a boundary to the local speed of sound.
- M is the local Mach number,
- u is the local flow velocity with respect to the boundaries (either internal, such as an object immersed in the flow, or external, like a channel), and
- c is the speed of sound in the medium, which in air varies with the square root of the thermodynamic temperature.
The local speed of sound, and hence the Mach number, depends on the temperature of the surrounding gas. The Mach number is primarily used to determine the approximation with which a flow can be treated as an incompressible flow. The medium can be a gas or a liquid. The boundary can be traveling in the medium, or it can be stationary while the medium flows along it, or they can both be moving, with different velocities: what matters is their relative velocity with respect to each other. The boundary can be the boundary of an object immersed in the medium, or of a channel such as a nozzle, diffuser or wind tunnel channeling the medium. As the Mach number is defined as the ratio of two speeds, it is a dimensionless number. If M < 0.2–0.3 and the flow is quasi-steady and isothermal, compressibility effects will be small and simplified incompressible flow equations can be used .
The Mach number is named after Austrian physicist and philosopher Ernst Mach, and is a designation proposed by aeronautical engineer Jakob Ackeret in 1929. As the Mach number is a dimensionless quantity rather than a unit of measure, the number comes after the unit; the second Mach number is Mach 2 instead of 2 Mach (or Machs). This is somewhat reminiscent of the early modern ocean sounding unit mark (a synonym for fathom), which was also unit-first, and may have influenced the use of the term Mach. In the decade preceding faster-than-sound human flight, aeronautical engineers referred to the speed of sound as Mach's number, never Mach 1

An F/A-18 Hornet creating a vapor cone at transonic speed just before reaching the speed of sound
Classification of Mach regimes
While the terms subsonic and supersonic, in the purest sense, refer to speeds below and above the local speed of sound respectively, aerodynamicists often use the same terms to talk about particular ranges of Mach values. This occurs because of the presence of a transonic regime around flight (free stream) M = 1 where approximations of the Navier-Stokes equations used for subsonic design no longer apply; the simplest explanation is that the flow around an airframe locally begins to exceed M = 1 even though the free stream Mach number is below this value.Meanwhile, the supersonic regime is usually used to talk about the set of Mach numbers for which linearised theory may be used, where for example the (air) flow is not chemically reacting, and where heat-transfer between air and vehicle may be reasonably neglected in calculations.
In the following table, the regimes or ranges of Mach values are referred to, and not the pure meanings of the words subsonic and supersonic.
Generally, NASA defines high hypersonic as any Mach number from 10 to 25, and re-entry speeds as anything greater than Mach 25. Aircraft operating in this regime include the Space Shuttle and various space planes in development.
High-speed flow around objects
Flight can be roughly classified in six categories:| Regime | Subsonic | Transonic | Sonic | Supersonic | Hypersonic | Hypervelocity |
|---|---|---|---|---|---|---|
| Mach | <0.8 | 0.8–1.3 | 1.0 | 1.3–5.0 | 5.0–10.0 | >10.0 |
At transonic speeds, the flow field around the object includes both sub- and supersonic parts. The transonic period begins when first zones of M > 1 flow appear around the object. In case of an airfoil (such as an aircraft's wing), this typically happens above the wing. Supersonic flow can decelerate back to subsonic only in a normal shock; this typically happens before the trailing edge. (Fig.1a)
As the speed increases, the zone of M > 1 flow increases towards both leading and trailing edges. As M = 1 is reached and passed, the normal shock reaches the trailing edge and becomes a weak oblique shock: the flow decelerates over the shock, but remains supersonic. A normal shock is created ahead of the object, and the only subsonic zone in the flow field is a small area around the object's leading edge. (Fig.1b)

|

|
| (a) | (b) |
When an aircraft exceeds Mach 1 (i.e. the sound barrier), a large pressure difference is created just in front of the aircraft. This abrupt pressure difference, called a shock wave, spreads backward and outward from the aircraft in a cone shape (a so-called Mach cone). It is this shock wave that causes the sonic boom heard as a fast moving aircraft travels overhead. A person inside the aircraft will not hear this. The higher the speed, the more narrow the cone; at just over M = 1 it is hardly a cone at all, but closer to a slightly concave plane.
At fully supersonic speed, the shock wave starts to take its cone shape and flow is either completely supersonic, or (in case of a blunt object), only a very small subsonic flow area remains between the object's nose and the shock wave it creates ahead of itself. (In the case of a sharp object, there is no air between the nose and the shock wave: the shock wave starts from the nose.)
As the Mach number increases, so does the strength of the shock wave and the Mach cone becomes increasingly narrow. As the fluid flow crosses the shock wave, its speed is reduced and temperature, pressure, and density increase. The stronger the shock, the greater the changes. At high enough Mach numbers the temperature increases so much over the shock that ionization and dissociation of gas molecules behind the shock wave begin. Such flows are called hypersonic.
It is clear that any object traveling at hypersonic speeds will likewise be exposed to the same extreme temperatures as the gas behind the nose shock wave, and hence choice of heat-resistant materials becomes important.
High-speed flow in a channel
As a flow in a channel becomes supersonic, one significant change takes place. The conservation of mass flow rate leads one to expect that contracting the flow channel would increase the flow speed (i.e. making the channel narrower results in faster air flow) and at subsonic speeds this holds true. However, once the flow becomes supersonic, the relationship of flow area and speed is reversed: expanding the channel actually increases the speed.The obvious result is that in order to accelerate a flow to supersonic, one needs a convergent-divergent nozzle, where the converging section accelerates the flow to sonic speeds, and the diverging section continues the acceleration. Such nozzles are called de Laval nozzles and in extreme cases they are able to reach hypersonic speeds (Mach 13 (15,926 km/h; 9,896 mph) at 20 °C).
An aircraft Machmeter or electronic flight information system (EFIS) can display Mach number derived from stagnation pressure (pitot tube) and static pressure.
Calculation
The Mach number at which an aircraft is flying can be calculated by- M is the Mach number
- u is velocity of the moving aircraft and
- c is the speed of sound at the given altitude
- qc is impact pressure (dynamic pressure) and
- p is static pressure
- is the ratio of specific heat of a gas at a constant pressure to heat at a constant volume (1.4 for air)
- is the is the specific gas constant for air.
WARP (Wing Angels Resources Planning)
Warp drive
A warp drive is a theoretical superluminal spacecraft propulsion system in many science fiction works, most notably Star Trek and I, Robot by Isaac Asimov. A spacecraft equipped with a warp drive may travel at speeds greater than that of light by many orders of magnitude. In contrast to some other fictitious Faster-than-light technologies such as a jump drive, the warp drive does not permit instantaneous travel between two points, but rather involves a measurable passage of time which is pertinent to the concept. In contrast to hyperdrive, spacecraft at warp velocity would continue to interact with objects in "normal space." The general concept of "warp drive" was introduced by John W. Campbell in his 1931 novel Islands of Space.
Einstein's theory of special relativity states that energy and mass are interchangeable, and speed of light travel is impossible for material objects that weigh more than photons. The problem of a material object exceeding light speed is that an infinite amount of kinetic energy would be required to travel at exactly the speed of light. This can theoretically be solved by warping space to move an object instead of increasing the kinetic energy of the object to do so. Such a solution to the faster than light travel problem leads to two directly opposite approaches to light-speed travel in science fiction: in the first, spaceships themselves are brought to light speed and beyond; in the second, not-yet-local space itself is made to come to the ship while the ship moves at sub-light speeds.

Transmission spacetunnel travel as envisioned by Les Bossinas for NASA
Star Trek
Original warp scale – The Original Series, The Animated Series, Enterprise, and Discovery
Warp effect as depicted in Star Trek: The Original Series
Warp effect as depicted in Star Trek: The Next Generation
The warp drive velocity in Star Trek is generally expressed in "warp factor" units, which—according to Star Trek Star Fleet Technical Manual—corresponds to the magnitude of the warp field. Achieving warp factor 1 is equal to breaking the light barrier, while the actual velocity corresponding to higher factors is determined using an ambiguous formula. According to the Star Trek episode writer's guide for The Original Series, warp factors are converted to multiples of the speed of light by multiplication with the cubic function of the warp factor itself. Accordingly, "warp 1" is equivalent to the speed of light, "warp 2" is eight times the speed of light, "warp 3" is 27 times the speed of light, etc. Several episodes of The Original Series placed the Enterprise in peril by having it travel at high warp factors. However, the velocity (in present dimensional units) of any given warp factor is rarely the subject of explicit expression, and travel times for specific interstellar distances are not consistent through the various series. In the Star Trek: The Next Generation Technical Manual it was written that the real warp speed depends on external factors such as particle density or electromagnetic fields and only roughly corresponds with the calculated speed of current warp factor. The reference work Star Trek Maps established the theory of subspace (or warp) highways. In certain regions, a spaceship can fly at a multiple of the speed that corresponds to the current warp factor.
In The Original Series, warp factor 6 was established as the common speed of the USS Enterprise NCC-1701. In some cases, the starship traveled at warp 7 or above, but with risk of damaging the ship or the engines. Warp 9 in The Original Series was the "never exceed" speed for the hulls and engines of Constitution-class starships, equivalent to the aircraft VNE V-speed. Warp 6 was the VNO "Normal Operation" maximum safe cruising speed for that vessel class. Only five stories in the original Star Trek series involved the Enterprise traveling beyond warp 9. In any instance, it was a result of the influence of alien beings or foreign technology. The warp 14.1 incident in That Which Survives was the result of runaway engines which brought the hull within seconds of structural failure before power was disengaged.
Later on, a prequel series titled Star Trek: Enterprise describes the warp engine technology as a "Gravimetric Field Displacement Manifold" (Commander Tucker's tour, "Cold Front"), and describes the device as being powered by a matter/anti-matter reaction which powers the two separate nacelles (one on each side of the ship) to create a displacement field. Enterprise, set in 2151 and onwards, follows the voyages of the first human ship capable of traveling at warp factor 5.2, which under the old warp table formula (the cube of the warp factor times the speed of light), is about 140 times the speed of light (i.e., 5.2 cubed). In the series pilot episode "Broken Bow", Capt. Archer equates warp 4.5 to "Neptune and back [from Earth] in six minutes" (which would correspond to a distance of 547 light-minutes or 66 au, consistent with Neptune's being a minimum of 29 au distant from Earth).
Modified warp scale – The Next Generation, Deep Space Nine and Voyager
Michael Okuda's new warp scale
In Star Trek: The Next Generation Technical Manual it was established that the normal operating speed of the Enterprise-D (Galaxy-class) was warp 6 (new scale), the maximum rated cruise was warp 9.2 and the maximum design speed of warp factor 9.6. In two episodes, the Enterprise-D could travel at warp 9.8 at "extreme risk", while fleeing from an enemy. According to the Star Trek: Deep Space Nine Technical Manual the Galaxy-class starships and some other starfleet vessels like Nebula-class or Excelsior-class were refitted during the Dominion War with newer technology including modifications which increased their maximum speed to warp 9.9.
According to the reference book USS Enterprise Owners' Workshop Manual the Enterprise-E can reach a maximum velocity of warp 9.95. The Star Trek: Starship Spotter reference book states that the Intrepid-class starship Voyager has a maximum sustainable cruising speed of warp 9.975, while the Prometheus-class can reach a maximum of warp 9.99, with maximum cruising speed of warp 9.9.
As stated in the collection Star Trek Fact Files, no ship, including highly developed ships like the Borg cube, may exceed warp factor 9.99 with her normal warp drive. To achieve higher speeds, the use of transwarp technology is required.
Warp velocities
In the book Star Trek Encyclopedia, some warp velocities are given directly. For comparison, the following table shows these values and also the calculated speeds of the original warp scale, the calculated speeds of a simplified Okuda scale and some canonical reference values for warp speeds from onscreen sources.| Warp factor |
Warp scale from Encyclopedia directly given values (Michael Okuda)[5] |
Cubic warp scale v = w3c (Franz Joseph)[6] |
Revised warp scale v = w10/3c (Michael Okuda)[7] |
Onscreen Reference (Canon) |
|---|---|---|---|---|
| (Multiple of speed of light) | ||||
| 1 | 1× | 1× | 1× | |
| 2 | 10× | 8× | 10× | In the Star Trek: Enterprise episode "Dead Stop", it is said that Enterprise would take about a decade (10 years) to travel 130 light years at warp 2. Thus warp 2 corresponds to about 13 times the speed of light. |
| 3 | 39× | 27× | 39× | In the Star Trek: The Next Generation episode "The Most Toys" the crew of Enterprise-D discovers that the android Data may have been stolen while on board another ship, Jovis. At this point the Jovis, which has a maximum warp factor of 3, has had a 23-hour head start, which the Enterprise-D figures puts her anywhere within a 0.102 light year radius of her last known position. (By conversion, this implies that warp 3 is equivalent to about 39c.) |
| 4 | 102× | 64× | 102× | In the Star Trek: Voyager episode "Resolutions", it is said that a Voyager shuttle would need about 700 years of flight time for a 70,000 light-year journey back to Earth. It follows that warp 4, the stated maximum speed of the shuttle, is about 100 times the speed of light. In the movie Star Trek: Beyond it is stated that the USS Franklin (NX-326) was the first Earth ship who was capable of warp 4. Montgomery Scott (Simon Pegg): "This is the USS Franklin, sir, can you believe it? First Earth ship capable of warp 4." It is unclear when the Franklin was first launched but it is speculated to be between 2145 and 2151. |
| 4.5 | 150× | 91× | 150× | In the Star Trek: Enterprise pilot "Broken Bow", Commander Tucker states "warp 4.5 next Thursday", to which Captain Archer responds "Neptune and back in six minutes". The distance from Earth to Neptune varies all the time as both planets orbit the sun, however the average distance between the two is around 30.63 au (4.58 billion km) and 29.76 au (4.45 billion km) average 4.52 billion km. Therefore, a round trip of 9.04 billion km in six minutes would imply that warp 4.5 is about 84 times the speed of light. |
| 5 | 213× | 125× | 213× | In the Star Trek: Enterprise episode "The Expanse", Captain Archer says the flight to the Delphic Expanse is equivalent to a three-month trip. Upon arrival of the Enterprise, the distance to Earth is given as 50 light years. Thus, warp 5, the maximum speed of the Enterprise, corresponds to about 200 times the speed of light. |
| 6 | 392× | 216× | 392× | |
| 7 | 656× | 343× | 656× | In the Star Trek: Enterprise episode "E²", the Enterprise will fly through an 11.6 light year long subspace corridor for a meeting with Degra. However, the Enterprise is thrown 127 years into the past. As the older Enterprise encounters their younger counterpart (to warn them), Captain Lorian suggests modifying the warp drive so that the younger Enterprise can briefly reach warp Factor 6.9 and cover this distance in about two days without using the corridor. Thus, warp 6.9 corresponds to about 2117 times the speed of light. In the Star Trek: Discovery episode "New Eden" (S2:E2), Commander Michael Burnham says a signal "is in the Beta Quadrant, 51,450 light years away," to which Captain Christopher Pike replies, "at top speed that would take us 150 years to get that far," indicating the maximum speed of the Discovery is 343 times the speed of light (51,450 light years / 150 years). That corresponds to warp 7 of the original warp scale. |
| 8 | 1024× | 512× | 1024× | |
| 9 | 1516× | 729× | 1516× | In the episode Bloodlines from the series Star Trek: The Next Generation, Riker claims that the Enterprise would need around 20 minutes for a 300 billion kilometer flight at warp 9. Thus warp 9 corresponds to a speed of 900 billion kilometers per hour (= 250 million kilometers per second) or about 830 times the speed of light. |
| 9.9 | 3053× | 970× | 2083× | In the episode The 37s from the Star Trek: Voyager series warp 9.9 is directly mentioned in a dialog with four billion miles per second (6.5 billion km per second), which is about 21,468 times faster than the speed of light. |
| 9.95 | 5000× | 985× | 2119× | |
| 9.975 | 6667× | 993× | 2137× | In the Voyager episode "Maneuvers", it is mentioned that the speed of the Voyager is approximately two billion kilometers per second, which is 6667 times the speed of light. According to Gene Roddenberry's first concept script Star Trek is ..., the original Enterprise had a maximum speed of 0.73 light years per hour, which is about 6395 times the speed of light. This corresponds roughly with warp 9.975 of the Okuda scale and the established maximum warp of the starship USS Voyager. |
| 9.99 | 7912× | 997× | 2147× | According to the episode Threshold from Star Trek: Voyager, warp 9.99 is the beginning of transwarp and the end of normal warp speeds. |
| 9.9999 | 199,516× | ~1000× | ~2154× | |
| 10 | Infinite velocity |
1000× | 2154× | In the episode "Threshold", Tom Paris breaks the warp 10 threshold, but travel beyond the threshold is later discovered to be unacceptably hazardous to biological life. In the episode "Where No One Has Gone Before" the Enterprise-D was shown to exceed warp 10, traveling 2.7 million light years from their home galaxy in a matter of minutes (though the ship's extreme velocity was due to the influence of an alien being and could not be achieved by starship engines). |
| 11 | Beyond scale |
1331× | 2960× | In episode The Changeling the Enterprise briefly reached warp factor 11, as a result of Nomad's "correction of inefficiencies" in the antimatter control system. In the episode By Any Other Name the Kelvans modified the Enterprise's engines for greater sustained speed of warp factor 11 to travel from the Milky Way Galaxy to the Andromeda Galaxy. |
| 12 | 1728× | 3956× | ||
| 13 | 2197× | 5166× | In the alternative future depicted in "All Good Things ...", the series finale of The Next Generation, the "future" Enterprise-D travels at warp 13, perhaps as a result of another reconfiguration of the warp scale. | |
| 14 | 2744× | 6613× | At one point in "That Which Survives" the Enterprise traveled at a warp factor of 14.1. | |
| 15 | 3375× | 8323× | ||
| 18.56 | 6395× | 16928× | According to Gene Roddenberry's first concept script Star Trek is ..., the original Enterprise had a maximum speed of 0.73 light years per hour, which is about 6395 times the speed of light. This corresponds with warp factor 18.56 of the cubic scale. | |
Transwarp
Transwarp generally refers to speeds and technologies that are beyond conventional warp drives. The warp drive has a natural physical or economical limit beyond which higher speeds are no longer possible. The reference work Star Trek Fact Files indicates this limit at warp factor 9.99. This is the highest conventional warp speed mentioned for a spaceship (Borg cube). Also in the episode Threshold (Star Trek Voyager) the warp factor 9.99 is suggested as the limit. This is the last warp factor mentioned before the leap takes place in the transwarp state.In the book Star Trek: The Next Generation Technical Manual the authors describes the idea of transwarp:
Finally, we had to create a back door for various powerful aliens like Q who got the knack of hurling the ship through the room for millions of light years during a commercial break.The transwarp concept itself is not tied to any particular technology or speed limit.
The first mention of a transwarp drive took place in the movie Star Trek III: The Search for Spock. There, the Starfleet developed a new spaceship type, the USS Excelsior (NX-2000), which should have a superior engine. The Excelsior captain plans to break the speed record of the USS Enterprise (warp 14.1 cubic scale). The principle of this drive is not explained. Later, in Star Trek VI: The Undiscovered Country, the USS Excelsior had a normal warp drive. In Star Trek Fact Files it is stated that the experiment was a failure and the spaceship was converted to a normal warp drive.
The entire episode Threshold from Star Trek Voyager is about a transwarp experiment by the USS Voyager crew. To get home faster, a shuttle is modified with novel dilithium crystals. The crew is trying to break the transwarp threshold. This threshold is between warp 9.99 and warp 10, and transwarp itself represented the infinite speed. The shuttle allegedly found itself at all points in the universe at the same time during the flight. However, the pilot suffers genetic mutations after the flight, so it is not repeated. Due to the shuttle's limited memory, only a small portion of the sensor data was recorded. The entire experiment is described in the reference work Star Trek Fact Files.
Some episodes later, fictionalized a few months later, the crew of USS Voyager encounters a species called the Voth. This species has spaceships with transwarp drive. However, this drive does not work on the basis of transwarp conduits, as the transwarp drive of the Borg, but is a further development of the conventional warp drive.
The mention of a second transwarp technology took place in the episode Descent of the series Star Trek: The Next Generation. A group of renegade Borg used transwarp conduits. These are wormhole-like tunnels through subspace. It was said in the dialogue that the flight through these tunnels was 20 times faster than the flight with maximum warp speed of the Enterprise. The flight itself was described as follows: "falling into a fast-moving river and getting swept away by the current." In the episode Endgame it is explained that the origin of these corridors was in six transwarp hubs spread across the galaxy. There were two ways to use these conduits outside these hubs. In The Next Generation, the Enterprise was able to open such a channel with a precisely modulated tachyon impulse, traveling 65 light-years. However, when the USS Voyager tried the same thing in Day of Honor, the attempt failed and almost destroyed the ship. The second possibility is the use of the transwarp coil. In episode Dark Frontier the crew of Voyager steals such a coil from the Borg and is able to shorten their journey home by 15 years, before the coil burns out.
Quantum slipstream
Another form of transwarp used in Star Trek is called Quantum Slipstream.Similar to the Borg transwarp conduits, the slipstream is a narrowly focused, directed field that is initiated by manipulating the fabric of the space-time continuum using the starship's navigational deflector array. This creates a subspace tunnel, which is projected ahead of the vessel. Once a ship has entered this tunnel, the forces inside propel it at incredible speed. To maintain the slipstream, a ship has to constantly modify the quantum field with its deflector dish. The speed of the drive is inversely proportional to the time and distance. When the crew enters the Dauntless in the episode Hope and Fear for the first time and accidentally activates the propulsion system, the spaceship flies a flight of 15 light-years over a period of about 10 seconds. That is equivalent to approximately 50 million times the speed of light. After realizing that they would have to leave Voyager forever to get home with the Dauntless, the crew tries to match the drive of the USS Voyager to the parameters of the Dauntless. The modified Voyager is able to cover a distance of 300 light years with the slipstream modification before the system becomes unstable. The way back to Earth is stated in a fake message, created by Arturis, with seven months aboard the Dauntless. For this period, the stocks are filled. At a residual distance of 60,000 light years at this time, this would correspond to a speed of about 100,000 times the speed of light or 1/500th of the time of a short slipstream jump.
However, in the episode "Timeless", the technology proved to be dangerously unstable, resulting in the loss of all hands of the Voyager in an alternate timeline. Due to a phase variance, the slipstream tunnel, produced by a replica slipstream drive of the Voyager, collapsed during the flight and the ship crashed on a planet near the border on the edge of the Delta Quadrant. Harry Kim and Chakotay survived, because they used the Delta Flyer, which flew ahead of the Voyager, and reached the Earth safely. They used, some years after this event, a temporal communication device to change the timeline and rescue the ship and the crew.
Folding space
In addition to the possibility to let a spaceship glide through space in a warp field, there is also space folding in Star Trek. Spatial folding means that two points of space-time are directly connected and an instantaneous change takes place. The space between is simply folded into a higher-dimensional hyperspace or subspace.In the episode That Which Survives of The Original Series, the Enterprise encountered the remains of people called Kalandans. These are able to instantaneously teleport spaceships as well as people over long distances.
In the episode Contagion of the series Star Trek: The Next Generation, the Enterprise-D discovered the former homeworld of the Iconians. These people were able to instantaneously teleport people over long distances with the help of Iconian Gateways. To ensure the gateway did not fall into the wrong hands, Captain Picard destroyed it.
A year later, in The High Ground, terrorists on the planet Rutia IV used a space folding teleporter called an inverter. However, this caused progressive physical harm to people during transport; multiple use almost always ended in death.
The USS Voyager came in touch with this technology several times on their way home. In the episode Prime Factors the crew tried to buy a Spatial Trajector from the Sikarians. This wraps an object in a kind of subspace bubble, and teleports it to another location using spatial folding. The range was 40,000 light-years. However, the technology was not compatible with the warp core and almost destroyed Voyager when it was used.
Three years later, in the episode Vis à Vis, Voyager discovered a stranded spaceship with a coaxial warp drive. This also used spatial folding for locomotion. But the system was very unstable and if there is a fault in the drive it could cause a tear in the space-time continuum. A replica of the drive was only tested in a shuttle and never used for the Voyager.
Last but not least, spatial folding appeared as a Geodesic Fold in the episode Inside Man. A geodesic fold occurs when a Verteron beam is fired at the atmosphere of a giant star at two different locations. This connects both points in space and creates a short lived passage. However, this was not usable because of deadly radiation that occurred during flight. A Ferengi ship's faked message from the Alpha Quadrant made the crew believe there was a safe passage. However, the Ferengi only wanted to get the Borg technology aboard Voyager and would have let the crew die. At the last moment, travel through the passage was aborted.
Fictional history
The episode "Metamorphosis", from The Original Series, establishes a backstory for the invention of warp drive on Earth, in which Zefram Cochrane discovered the "space warp". Cochrane is repeatedly referred to afterwards, but the exact details of the first warp trials were not shown until the second Star Trek: The Next Generation movie, Star Trek: First Contact. The movie depicts Cochrane as having first operated a warp drive on Earth in 2063. This successful first trial led directly to first contact with the Vulcans.It was also established that many other civilizations had warp drive before humans; First Contact co-writer Ronald D. Moore suggested Cochrane's drive was in some way superior to forms which existed beforehand, and was gradually adopted by the galaxy at large.
Slingshot effect
The "slingshot effect" is first depicted in "Tomorrow Is Yesterday" (1967) as a method of time travel. The procedure involves traveling at a high warp velocity in the proximity to a star, on a precisely calculated "slingshot" path; if successful, it causes a ship to enter a time warp, leading to the past or future. The same technique is used in the episode "Assignment: Earth" (1968) for historic research. The term "time warp" was first used in "The Naked Time" (1966) when a previously untried cold-start intermix of matter and antimatter threw the Enterprise back three days in time. The term was later used in Star Trek IV in describing the slingshot effect. The technique was mentioned as a viable method of time travel in The Next Generation episode "Time Squared" (1989). The equations used to calculate the time warp trajectory are extremely complicated, understood only by a select few, with even the most miniscule error resulting in catastrophe.This "slingshot" effect has been explored in theoretical physics: it is hypothetically possible to slingshot oneself "around" the event horizon of a black hole. As a result of the black hole's extreme gravitation, time would pass at a slower rate near the event horizon, relative to the outside universe; the traveler would experience the passage of only several minutes or hours, while hundreds of years would pass in 'normal' space.
Warp core
A primary component of the warp drive method of propulsion in the Star Trek universe is the "gravimetric field displacement manifold", more commonly referred to as a warp core. It is a fictional reactor that taps the energy released in a matter-antimatter annihilation to provide the energy necessary to power a starship's warp drive, allowing faster-than-light travel. Starship warp cores generally also serve as powerplants for other primary ship systems.When matter and antimatter come into contact, they annihilate—both matter and antimatter are converted directly and entirely into enormous quantities of energy, in the form of subnuclear particles and electromagnetic radiation (specifically, mesons and gamma rays). In the Star Trek universe, fictional "dilithium crystals" are used to regulate this reaction. These crystals are described as being non-reactive to anti-matter when bombarded with high levels of radiation.
Usually, the reactants are deuterium, which is an isotope of hydrogen, and antideuterium (its antimatter counterpart). In The Original Series and in-universe chronologically subsequent series, the warp core reaction chamber is often referred to as the "dilithium intermix chamber" or the "matter/antimatter reaction chamber", depending upon the ship's intermix type. The reaction chamber is surrounded by powerful magnetic fields to contain the anti-matter. If the containment fields ever fail, the subsequent interaction of the antimatter fuel with the container walls would result in a catastrophic release of energy, with the resultant explosion capable of utterly destroying the ship. Such "warp core breaches" are used as plot devices in many Star Trek episodes. An intentional warp core breach can also be deliberately created, as one of the methods by which a starship can be made to self-destruct.
The mechanism that provides a starship's propulsive force is the "warp nacelle", a cylindrical pod (or pods) offset from the hull. Nacelles generate the actual "warp bubble" outside the ship; destruction of a nacelle will cripple the ship and possibly cause a warp core breach.
Real-world theories and science
In 1994, physicist Miguel Alcubierre formulated a theoretical solution, called the Alcubierre drive, for faster-than-light travel which models the warp drive concept. Calculations found that such a model would require prohibitive amounts of negative energy or mass.In 2012, NASA researcher Harold White hypothesized that by changing the shape of the warp drive, much less negative mass and energy could be used, though the energy required ranges from the mass of Voyager 1 to the mass of the observable universe, or many orders of magnitude greater than anything currently possible by modern technology. NASA engineers have begun preliminary research into such technology.
In 2018, the U.S. Defense Intelligence Agency made public a 2010 report that surveyed multiple different approaches to faster-than-light travel. Caltech professor Sean Carroll, who reviewed the report, explained that, while the theories were legitimate, they did not represent "something that's going to connect with engineering anytime soon, probably anytime ever."

Warp requirements for 10m OD sphere
Warp-field experiments
Warp-field experiments are a series of current and proposed experiments to create and detect instances of spacetime warping. The ultimate goal is to prove or disprove the possibility of spacetime metric engineering with reasonable amounts of energy.Motivation
Visualisation of York time, a measurement of spacetime curvature as induced by the Alcubierre metric.
Difficulties
Einstein's field equations show that comparatively high amounts of energy are required for any significant curvature of spacetime under ordinary conditions. With the energy-requirement-decreasing concepts only being partially implemented yet, the available measurement methods are reaching the limits of what is technically possible. That is why current results remain mostly inconclusive until measurements can be further refined or the effect can be increased. New experimental setups have been proposed to boost sensitivity, and using the higher-dimensional yet still purely theoretical approach may increase any effect sufficiently to obtain significant results to prove or disprove the theory.Current and proposed experiments
Conceptual warp-field-interferometer test configuration from White's and Davis's 2006 STAIF conference proceedings
A time-of-flight experiment was proposed in 2013 using a modified Fabry–Pérot interferometer.
How Warp Speed Works

NASA
An artist's rendition of what warp speed might look like to a space traveler.
The captain adjusts the ship's warp drive appropriately, and you settle in for warp speed. Traveling faster than the speed of light, you should arrive to your destination in just a few minutes.
For as long as humans have looked up to the skies, space has fascinated us, and astronomers and philosophers alike have asked the most fundamental questions while staring at the stars. What are we doing here, anyway? How did the universe begin, and are there other, parallel universes that mirror ours? Is there life out there in other galaxies, and what would it be like to travel there? While we haven't quite answered these questions yet, we at least have science fiction like "Star Trek" to test the human imagination. Everything from H.G. Wells' "The Time Machine" to "Star Trek" to Joss Whedon's "Firefly" series has touched on the possibilities of time travel, teleportation and, of course, warp speed. But how does something like warp speed fit into reality and our universe? Is warp speed just a wacky science fiction device, or is it theoretically possible? How does it work in the "Star Trek" universe? For everything on warp speed, infinity and beyond,
Newton's Third Law of Motion
When the writers of "Star Trek" sat down to plan the series, they found themselves confronted with a few problems. They were essentially creating a space opera, a subgenre of science fiction that takes place in space and covers the span of several galaxies and millions of light years. The "Star Wars" films are another example of the space opera subgenre. As the "opera" part of the name suggests, a show like "Star Trek" isn't meant to be slow or ordinary -- when people think of the series, they probably think of melodramatic plots involving aliens, space travel and action-packed laser fights.
So the creator of the series, Gene Roddenberry, and the other writers had to find a way to move the show's characters around the universe in a timely, dramatic fashion. At the same time, they wanted to do their best to stick to the laws of physics. The biggest problem was that even if a starship could travel at the speed of light, the time to go from one galaxy to another could still take hundreds, maybe thousands of years. A journey from the Earth to the center of our galaxy, for example, would take about 25,000 years if you were to travel just under the speed of light. This, of course, wouldn't make very exciting television.
The invention of warp speed solved the opera part of the problem, since it allowed the Enterprise to go much faster than the speed of light. But what was the explanation? How could they explain an object traveling faster than the speed of light, something Einstein proved impossible in his Special Theory of Relativity?

Eliot J. Schechter/Getty Images
When this shuttle makes its way into orbit, it will travel at about 17,000 miles per hour. Humans can withstand this velocity in this type of shuttle, but if the shuttle even attempted to approach the speed of light, the effect would prove fatal to astron
You feel this law come into play every time you accelerate in a car or fly in an airplane. As the vehicle speeds up and moves forward, you feel pressure on your seat. The seat is pushing on you, but you're also exerting a force against the seat.
So what does this have to do with "Star Trek" and the Enterprise? Even if it were possible to accelerate to something like half the speed of light, such intense acceleration would kill a person by smashing him against his seat. Even though he'd be pushing back with an equal and opposite force, his mass compared to the starship is just too small -- the same kind of thing happens when a mosquito hits your windshield and splatters. So how can the Enterprise possibly go faster than the speed of light without killing the members on board?
Einstein, Relativity and the Space-time Continuum
It's important to understand Einstein's work on the space-time continuum and how it relates to the Enterprise traveling through space. In his Special Theory of Relativity, Einstein states two postulates:
- The speed of light (about 300,000,000 meters per second) is the same for all observers, whether or not they're moving.
- Anyone moving at a constant speed should observe the same physical laws.
What does this mean for the Captain Kirk and his team? The closer an object gets to the speed of light, that object actually experiences time at a significantly slower rate. If the Enterprise were traveling safely at close to the speed of light to the center of our galaxy from Earth, it would take 25,000 years of Earth time. For the crew, however, the trip would probably only take 10 years.
Although that timeframe might be possible for the individuals onboard, we're presented with yet another problem -- a Federation attempting to run an intergalactic civilization would run into some problems if it took 50,000 years for a starship to hit the center of our galaxy and come back.
So the Enterprise has to avoid the speed of light in order to keep the passengers onboard in synch with Federation time. At the same time, it also must reach speeds faster than that of light in order to move around the universe in an efficient manner. Unfortunately, as Einstein states in his Special Theory of Relativity, nothing is faster than the speed of light. Space travel therefore would be impossible if we're looking at the special relativity.
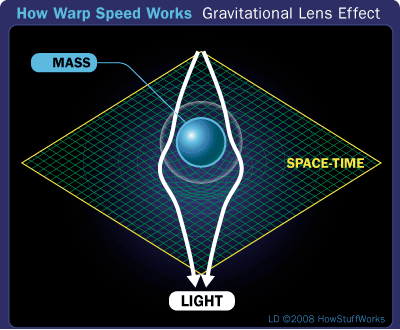
According to Einstein's General Theory of Relativity, matter bends the fabric of space and time. The distortion of the space-time continuum even affects the behavior of light.
The Warp Drive
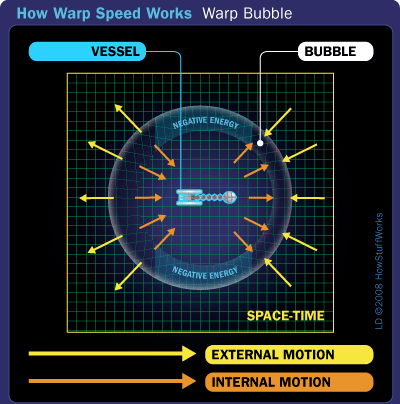
A warp bubble surrounding a starship, which protects the ship and crew members as space and time distorts.
In the "Star Trek" universe, warp speed is accomplished through the use of a warp drive. The warp drive is powered by matter-antimatter reactions, which are regulated by a substance called dilithium. This reaction creates highly-energetic plasma known as electro-plasma, a type of matter with its own magnetic field, which reacts with the starship's warp coils. The warp coils are typically enclosed in what the "Star Trek" writers call a warp nacelle. The whole package creates a "warp field" or "bubble" around the Enterprise, allowing the ship and its crew to remain safe while space manipulates around them.
Sometime between the first television series ("Star Trek: The Original Series") and the second ("Star Trek: The Next Generation"), the writers decided to assign a limit to warp speed -- using a scale of Warp-1 to Warp-10, the Enterprise wasn't allowed to travel just anywhere at anytime, seeing as that would make plotting too easy. In the show, Warp-10 became an impossible maximum speed, an infinity in which the starship would be at all points in the universe at the same time. Warp-9.6, according to the "Next Generation" technical manual, is the highest attainable speed allowed -- it's set at 1,909 times the speed of light. Although there are some inconsistencies, the following list the different speeds in the "Star Trek" universe:
| Warp Factor | Number of times the speed of light |
| 1 | 1 |
| 2 | 10 |
| 3 | 39 |
| 4 | 102 |
| 5 | 215 |
| 6 | 392 |
| 7 | 656 |
| 8 | 1,024 |
| 9 | 1,516 |
| 9.6 | 1,909 |
| 10 | Infinity |
Problems with Warp Speed
Physicist Miguel Alcubierre has suggested the use of so-called "exotic matter," a theoretical type of matter with negative energy. If it could be found or created, the exotic matter would do the job of repelling space and time and creating the gravitational field.
Unfortunately, that's as far as it goes for possible fuel sources -- there are more problems than solutions when it comes to the concept of powering warp speed. Even if the Enterprise were to travel at sublight speeds, known as impulse drive to "Star Trek" fans, the amount of fuel and energy needed to travel quickly through space would be too much for a single starship. The impulse drive of the Enterprise is powered by nuclear fusion, the same kind of reaction that lights up the sun and creates huge explosions from certain nuclear bombs. According to Dr. Lawrence Krauss, a theoretical physicist and author of "The Physics of Star Trek," if Captain Kirk wanted to travel at half the speed of light (150,000 kilometers per second), the starship would need to burn 81 times its mass in hydrogen, the fuel used for nuclear fusion. The technical manual for "Star Trek: The Next Generation" lists the Enterprise as more than 4 million metric tons in weight, so the ship would need more than 300 million metric tons of hydrogen just to move forward. Of course, to slow down to a stop, the starship would need yet another 300 million metric tons of fuel, and a potential trip across galaxies would need 6,642 times the mass of the "Enterprise."
Some people have proposed a system in which a device gathers hydrogen as the starship travels, foregoing the necessity to store huge amounts of fuel, but Krauss suggests this device would have to be about 25 miles wide to capture anything worth using. Even though hydrogen is the most abundant element in the galaxy, there's only about one atom of hydrogen for every cubic square inch.
Making the warp drive work would be another thing. The warp drive in "Star Trek" gets its power by reacting matter with antimatter -- the result is complete annihilation and the release of pure energy. Since antimatter isn't very common throughout our universe, the Federation would have to produce it, something we can do today at the Fermi National Accelerator Laboratory (Fermilab) in Illinois. Again, the problem turns out to be a issue of the amount of fuel necessary to power a warp drive. Kruass notes that Fermilab is capable of producing 50 billion antiprotons in one hour -- enough to produce 1/1000 of a watt. You would need 100,000 Fermilabs to power a single light bulb. Producing enough antiprotons to bend the space-time continuum looks near impossible as far as our current technology goes.
Although there's little chance during this century of humans developing a spaceship that could bend space and travel to distant galaxies faster than the speed of light, this hasn't stopped scientists and fans of the series alike to think about the potential. As recent as November 2007, the British Interplanetary Society brought together several physicists for a conference called "Faster Than Light: Breaking the Interstellar Distance Barrier" .
The Science of "Star Trek"
As far as science fiction goes, "Star Trek" is well regarded by its
fans for sticking to relatively plausible physics. Although no one's
come up with a starship that would travel at warp speed, no one's
disproved the possibility of such a feat. "Star Trek" has also looked
at other big concepts throughout the series, including the notion of time travel through black holes
or wormholes. The writers also get several nitpicky details correct,
such as the fact that there is no sound in space. While George Lucas
includes laser blasts and explosions throughout his "Star Wars" series
in order to keep things dramatic, "Star Trek" kept a bit closer to
reality by not including sound effects in space. ____________________________________________________
Artificial Intelligence In Humanoid Robots
When people think of Artificial
Intelligence (AI), the major image that pops up in their heads is that
of a robot gliding around and giving mechanical replies. There are many
forms of AI but humanoid robots are one of the most popular forms. They
have been depicted in several Hollywood movies and if you are a fan of
science fiction, you might have come across a few humanoids. One of the
earliest forms of humanoids was created in 1495 by Leonardo Da Vinci. It
was an armor suit and it could perform a lot of human functions such as
sitting, standing and walking. It even moved as though a real human was
inside it.
Initially, the major aim of AI for humanoids was for research
purposes. They were being used for research on how to create better
prosthetics for humans. Now, humanoids are being created for several
purposes that are not limited to research. Modern-day humanoids are
developed to carry out different human tasks and occupy different roles
in the employment sector. Some of the roles they could occupy are the
role of a personal assistant, receptionist, front desk officer and so
on.The process of inventing a humanoid is quite complex and a lot of work and research is put into the process. Most times, inventors and engineers face some challenges. First-grade sensors and actuators are very important and a tiny mistake could result in glitching. Humanoids move, talk and carry out actions through certain features such as sensors and actuators.
People assume that humanoid robots are robots that are structurally similar to human beings. That is, they have a head, torso, arms and legs. However, this is not always the case as some humanoids do not completely resemble humans. Some are modeled after only some specific human parts such as the human head. Humanoids are usually either Androids or Gynoids. An Android is a humanoid robot designed to resemble a male human while gynoids look like female humans.
Humanoids work through certain features. They have sensors that aid them in sensing their environments. Some have cameras that enable them to see clearly. Motors placed at strategic points are what guide them in moving and making gestures. These motors are usually referred to as actuators.
The human body is studied and examined first to get a clear picture of what is about to be imitated. Then, one has to determine the task or purpose the humanoid is being created for. Humanoid robots are created for several purposes. Some are created strictly for experimental or research purposes. Others are created for entertainment purposes. Some humanoids are created to carry out specific tasks such as the tasks of a personal assistant using AI, helping out at elderly homes, and so on.
fully functional humanoid is ready is creating mechanisms similar to human body parts and testing them. Then, they have to go through the coding process which is one of the most vital stages in creating a humanoid. Coding is the stage whereby these inventors program the instructions and codes that would enable the humanoid to carry out its functions and give answers when asked a question.
Some of these challenges include:
- Actuators: These are the motors that help in motion and making gestures. The human body is dynamic. You can easily pick up a rock, toss it across the street, spin seven times and do the waltz. All these can happen in the space of ten to fifteen seconds. To make a humanoid robot, you need strong, efficient actuators that can imitate these actions flexibly and within the same time frame or even less. The actuators should be efficient enough to carry a wide range of actions.
- Sensors: These are what help the humanoids to sense their environment. Humanoids need all the human senses: touch, smell, sight, hearing and balance to function properly. The hearing sensor is important for the humanoid to hear instructions, decipher them and carry them out. The touch sensor prevents it from bumping into things and causing self-damage. The humanoid needs a sensor to balance movement and equally needs heat and pain sensors to know when it faces harm or is being damaged. Facial sensors also need to be intact for the humanoid to make facial expressions, and these sensors should be able to carry a wide range of expressions.
- AI-based Interaction: The level at which humanoid robots can interact with humans is quite limited. This where Artificial Intelligence is critical. It can help decipher commands, questions, statements and might even be able to give witty, sarcastic replies and understand random, ambiguous human ramblings.









_________________________________________________________________________________
The function area in space and time goes outside of space and time
Quantum mechanics can answer this question. Relativity defines the differential structure of space-time (metric) without giving any indications about the boundary. This suggests that relativity is a correct but not a complete theory (a well-formulated mathematical problem, i.e. Dirichlet problem, needs differential equations and boundary conditions). Is it possible that quantum mechanics is the manifestation of microscopic boundary conditions of space-time? Recent papers, e.g. see attached "Elementary space-time cycles" , absolutely confirm the viability of this unified description of quantum and relativistic mechanics.
Philosophy of space and time is the branch of philosophy concerned with the issues surrounding the ontology, epistemology, and character of space and time. While such ideas have been central to philosophy from its inception, the philosophy of space and time was both an inspiration for and a central aspect of early analytic philosophy. The subject focuses on a number of basic issues, including whether time and space exist independently of the mind, whether they exist independently of one another, what accounts for time's apparently unidirectional flow, whether times other than the present moment exist, and questions about the nature of identity (particularly the nature of identity over time).
Mach
Another important figure in this debate is 19th-century physicist Ernst Mach. While he did not deny the existence of phenomena like that seen in the bucket argument, he still denied the absolutist conclusion by offering a different answer as to what the bucket was rotating in relation to: the fixed stars.Mach suggested that thought experiments like the bucket argument are problematic. If we were to imagine a universe that only contains a bucket, on Newton's account, this bucket could be set to spin relative to absolute space, and the water it contained would form the characteristic concave surface. But in the absence of anything else in the universe, it would be difficult to confirm that the bucket was indeed spinning. It seems equally possible that the surface of the water in the bucket would remain flat.
Mach argued that, in effect, the water experiment in an otherwise empty universe would remain flat. But if another object were introduced into this universe, perhaps a distant star, there would now be something relative to which the bucket could be seen as rotating. The water inside the bucket could possibly have a slight curve. To account for the curve that we observe, an increase in the number of objects in the universe also increases the curvature in the water. Mach argued that the momentum of an object, whether angular or linear, exists as a result of the sum of the effects of other objects in the universe (Mach's Principle).
Einstein
Albert Einstein proposed that the laws of physics should be based on the principle of relativity. This principle holds that the rules of physics must be the same for all observers, regardless of the frame of reference that is used, and that light propagates at the same speed in all reference frames. This theory was motivated by Maxwell's equations, which show that electromagnetic waves propagate in a vacuum at the speed of light. However, Maxwell's equations give no indication of what this speed is relative to. Prior to Einstein, it was thought that this speed was relative to a fixed medium, called the luminiferous ether. In contrast, the theory of special relativity postulates that light propagates at the speed of light in all inertial frames, and examines the implications of this postulate.All attempts to measure any speed relative to this ether failed, which can be seen as a confirmation of Einstein's postulate that light propagates at the same speed in all reference frames. Special relativity is a formalization of the principle of relativity that does not contain a privileged inertial frame of reference, such as the luminiferous ether or absolute space, from which Einstein inferred that no such frame exists.
Einstein generalized relativity to frames of reference that were non-inertial. He achieved this by positing the Equivalence Principle, which states that the force felt by an observer in a given gravitational field and that felt by an observer in an accelerating frame of reference are indistinguishable. This led to the conclusion that the mass of an object warps the geometry of the space-time surrounding it, as described in Einstein's field equations.
In classical physics, an inertial reference frame is one in which an object that experiences no forces does not accelerate. In general relativity, an inertial frame of reference is one that is following a geodesic of space-time. An object that moves against a geodesic experiences a force. An object in free fall does not experience a force, because it is following a geodesic. An object standing on the earth, however, will experience a force, as it is being held against the geodesic by the surface of the planet.
Einstein partially advocates Mach's principle in that distant stars explain inertia because they provide the gravitational field against which acceleration and inertia occur. But contrary to Leibniz's account, this warped space-time is as integral a part of an object as are its other defining characteristics, such as volume and mass. If one holds, contrary to idealist beliefs, that objects exist independently of the mind, it seems that relativistics commits them to also hold that space and temporality have exactly the same type of independent existence.
Building from a mix of insights from the historical debates of absolutism and conventionalism as well as reflecting on the import of the technical apparatus of the General Theory of Relativity, details as to the structure of space-time have made up a large proportion of discussion within the philosophy of space and time, as well as the philosophy of physics. The following is a short list of topics.
Relativity of simultaneity
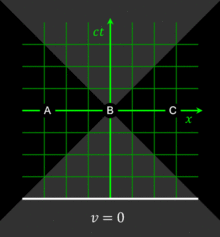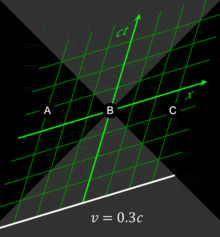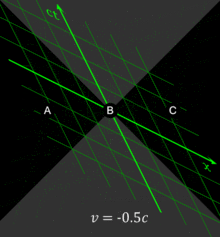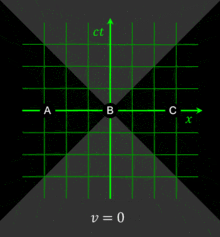
According to special relativity each point in the universe can have a different set of events that compose its present instant. This has been used in the Rietdijk–Putnam argument to demonstrate that relativity predicts a block universe in which events are fixed in four dimensions.[citation needed]Invariance vs. covariance
Bringing to bear the lessons of the absolutism/relationalism debate with the powerful mathematical tools invented in the 19th and 20th century, Michael Friedman draws a distinction between invariance upon mathematical transformation and covariance upon transformation.Invariance, or symmetry, applies to objects, i.e. the symmetry group of a space-time theory designates what features of objects are invariant, or absolute, and which are dynamical, or variable.
Covariance applies to formulations of theories, i.e. the covariance group designates in which range of coordinate systems the laws of physics hold.
This distinction can be illustrated by revisiting Leibniz's thought experiment, in which the universe is shifted over five feet. In this example the position of an object is seen not to be a property of that object, i.e. location is not invariant. Similarly, the covariance group for classical mechanics will be any coordinate systems that are obtained from one another by shifts in position as well as other translations allowed by a Galilean transformation.
In the classical case, the invariance, or symmetry, group and the covariance group coincide, but they part ways in relativistic physics. The symmetry group of the general theory of relativity includes all differentiable transformations, i.e., all properties of an object are dynamical, in other words there are no absolute objects. The formulations of the general theory of relativity, unlike those of classical mechanics, do not share a standard, i.e., there is no single formulation paired with transformations. As such the covariance group of the general theory of relativity is just the covariance group of every theory.
Historical frameworks
A further application of the modern mathematical methods, in league with the idea of invariance and covariance groups, is to try to interpret historical views of space and time in modern, mathematical language.In these translations, a theory of space and time is seen as a manifold paired with vector spaces, the more vector spaces the more facts there are about objects in that theory. The historical development of spacetime theories is generally seen to start from a position where many facts about objects are incorporated in that theory, and as history progresses, more and more structure is removed.
For example, Aristotelian space and time has both absolute position and special places, such as the center of the cosmos, and the circumference. Newtonian space and time has absolute position and is Galilean invariant, but does not have special positions.
Holes
With the general theory of relativity, the traditional debate between absolutism and relationalism has been shifted to whether spacetime is a substance, since the general theory of relativity largely rules out the existence of, e.g., absolute positions. One powerful argument against spacetime substantivalism, offered by John Earman is known as the "hole argument".This is a technical mathematical argument but can be paraphrased as follows:
Define a function d as the identity function over all elements over the manifold M, excepting a small neighbourhood H belonging to M. Over H d comes to differ from identity by a smooth function.
With use of this function d we can construct two mathematical models, where the second is generated by applying d to proper elements of the first, such that the two models are identical prior to the time t=0, where t is a time function created by a foliation of spacetime, but differ after t=0.
These considerations show that, since substantivalism allows the construction of holes, that the universe must, on that view, be indeterministic. Which, Earman argues, is a case against substantivalism, as the case between determinism or indeterminism should be a question of physics, not of our commitment to substantivalism.
Direction of time
The problem of the direction of time arises directly from two contradictory facts. Firstly, the fundamental physical laws are time-reversal invariant; if a cinematographic film were taken of any process describable by means of the aforementioned laws and then played backwards, it would still portray a physically possible process. Secondly, our experience of time, at the macroscopic level, is not time-reversal invariant. Glasses can fall and break, but shards of glass cannot reassemble and fly up onto tables. We have memories of the past, and none of the future. We feel we can't change the past but can influence the future.Spacetime
Until the 20th century, it was assumed that the three-dimensional geometry of the universe (its spatial expression in terms of coordinates, distances, and directions) was independent of one-dimensional time. However, in 1905, Albert Einstein based his seminal work on special relativity on two postulates:
- The laws of physics are invariant (i.e., identical) in all inertial systems (i.e., non-accelerating frames of reference)
- The speed of light in a vacuum is the same for all observers, regardless of the motion of the light source.
Einstein framed his theory in terms of kinematics (the study of moving bodies). His theory was a breakthrough advance over Lorentz's 1904 theory of electromagnetic phenomena and Poincaré's electrodynamic theory. Although these theories included equations identical to those that Einstein introduced (i.e. the Lorentz transformation), they were essentially ad hoc models proposed to explain the results of various experiments—including the famous Michelson–Morley interferometer experiment—that were extremely difficult to fit into existing paradigms.
In 1908, Hermann Minkowski—once one of the math professors of a young Einstein in Zürich—presented a geometric interpretation of special relativity that fused time and the three spatial dimensions of space into a single four-dimensional continuum now known as Minkowski space. A key feature of this interpretation is the formal definition of the spacetime interval. Although measurements of distance and time between events differ for measurements made in different reference frames, the spacetime interval is independent of the inertial frame of reference in which they are recorded.
Minkowski's geometric interpretation of relativity was to prove vital to Einstein's development of his 1915 general theory of relativity . wherein he showed how mass and energy curve flat spacetime into a pseudo-Riemannian manifold.
Each location in spacetime is marked by four numbers defined by a frame of reference: the position in space, and the time (which can be visualized as the reading of a clock located at each position in space). The 'observer' synchronizes the clocks according to their own reference frame.
. Michelson and Morley expected that motion through the aether would cause a differential phase shift between light traversing the two arms of their apparatus. The most logical explanation of their negative result, aether dragging, was in conflict with the observation of stellar aberration.
Spacetime interval
In three-dimensions, the distance between two points can be defined using the Pythagorean theorem:In special relativity, however, the distance between two points is no longer the same if measured by two different observers when one of the observers is moving, because of Lorentz contraction. The situation is even more complicated if the two points are separated in time as well as in space. For example, if one observer sees two events occur at the same place, but at different times, a person moving with respect to the first observer will see the two events occurring at different places, because (from their point of view) they are stationary, and the position of the event is receding or approaching. Thus, a different measure must be used to measure the effective "distance" between two events.
In four-dimensional spacetime, the analog to distance is the interval. Although time comes in as a fourth dimension, it is treated differently than the spatial dimensions. Minkowski space hence differs in important respects from four-dimensional Euclidean space. The fundamental reason for merging space and time into spacetime is that space and time are separately not invariant, which is to say that, under the proper conditions, different observers will disagree on the length of time between two events (because of time dilation) or the distance between the two events (because of length contraction). But special relativity provides a new invariant, called the spacetime interval, which combines distances in space and in time. All observers who measure time and distance carefully will find the same spacetime interval between any two events. Suppose an observer measures two events as being separated in time by and a spatial distance . Then the spacetime interval between the two events that are separated by a distance in space and by in the -coordinate is:
- , or for three space dimensions,
Note on nomenclature: Although for brevity, one frequently sees interval expressions expressed without deltas, including in most of the following discussion, it should be understood that in general, means , etc. We are always concerned with differences of spatial or temporal coordinate values belonging to two events, and since there is no preferred origin, single coordinate values have no essential meaning.
Figure
2-1. Spacetime diagram illustrating two photons, A and B, originating
at the same event, and a slower-than-light-speed object, C
Because of the minus sign, the spacetime interval between two distinct events can be zero. If is positive, the spacetime interval is timelike, meaning that two events are separated by more time than space. If is negative, the spacetime interval is spacelike, meaning that two events are separated by more space than time. Spacetime intervals are zero when . In other words, the spacetime interval between two events on the world line of something moving at the speed of light is zero. Such an interval is termed lightlike or null. A photon arriving in our eye from a distant star will not have aged, despite having (from our perspective) spent years in its passage.
A spacetime diagram is typically drawn with only a single space and a single time coordinate. Fig. 2‑1 presents a spacetime diagram illustrating the world lines (i.e. paths in spacetime) of two photons, A and B, originating from the same event and going in opposite directions. In addition, C illustrates the world line of a slower-than-light-speed object. The vertical time coordinate is scaled by so that it has the same units (meters) as the horizontal space coordinate. Since photons travel at the speed of light, their world lines have a slope of ±1. In other words, every meter that a photon travels to the left or right requires approximately 3.3 nanoseconds of time.
Note on nomenclature: There are two sign conventions in use in the relativity literature:
- and
Reference frames
Figure 2-2. Galilean diagram of two frames of reference in standard configuration
Figure
2-3. (a) Galilean diagram of two frames of reference in standard
configuration, (b) spacetime diagram of two frames of reference, (c)
spacetime diagram showing the path of a reflected light pulse
- The x, y, z axes of frame S are oriented parallel to the respective primed axes of frame S′.
- Frame S′ moves in the x-direction of frame S with a constant velocity v as measured in frame S.
- The origins of frames S and S′ are coincident when time t = 0 for frame S and t′ = 0 for frame S′.
The same events P, Q, R are plotted in Fig. 2‑3b in the frame of observer O. The light paths have slopes = 1 and −1 so that △PQR forms a right triangle. Since OP = OQ = OR, the angle between x′ and x must also be θ.
While the rest frame has space and time axes that meet at right angles, the moving frame is drawn with axes that meet at an acute angle. The frames are actually equivalent. The asymmetry is due to unavoidable distortions in how spacetime coordinates can map onto a Cartesian plane, and should be considered no stranger than the manner in which, on a Mercator projection of the Earth, the relative sizes of land masses near the poles (Greenland and Antarctica) are highly exaggerated relative to land masses near the Equator.
Relativity of simultaneity
Figure 2-6. Animation illustrating relativity of simultaneity
Fig. 2-6 illustrates the use of spacetime diagrams in the analysis of the relativity of simultaneity. The events in spacetime are invariant, but the coordinate frames transform as discussed above for Fig. 2‑3. The three events (A, B, C) are simultaneous from the reference frame of an observer moving at v = 0. From the reference frame of an observer moving at v = 0.3 c, the events appear to occur in the order C, B, A. From the reference frame of an observer moving at v = −0.5 c, the events appear to occur in the order A, B, C. The white line represents a plane of simultaneity being moved from the past of the observer to the future of the observer, highlighting events residing on it. The gray area is the light cone of the observer, which remains invariant.
A spacelike spacetime interval gives the same distance that an observer would measure if the events being measured were simultaneous to the observer. A spacelike spacetime interval hence provides a measure of proper distance, i.e. the true distance = Likewise, a timelike spacetime interval gives the same measure of time as would be presented by the cumulative ticking of a clock that moves along a given world line. A timelike spacetime interval hence provides a measure of the proper time = .
. Lunar laser ranging experiment. (left) This retroreflector was left on the Moon by astronauts on the Apollo 11 mission. (right) Astronomers all over the world have bounced laser light off the retroreflectors left by Apollo astronauts and Russian lunar rovers to measure precisely the Earth-Moon distance.
Technical topics
Is spacetime really curved?
In Poincaré's conventionalist views, the essential criteria according to which one should select a Euclidean versus non-Euclidean geometry would be economy and simplicity. A realist would say that Einstein discovered spacetime to be non-Euclidean. A conventionalist would say that Einstein merely found it more convenient to use non-Euclidean geometry. The conventionalist would maintain that Einstein's analysis said nothing about what the geometry of spacetime really is.Such being said,
- 1. Is it possible to represent general relativity in terms of flat spacetime?
- 2. Are there any situations where a flat spacetime interpretation of general relativity may be more convenient than the usual curved spacetime interpretation?
The flat spacetime paradigm posits that matter creates a gravitational field that causes rulers to shrink when they are turned from circumferential orientation to radial, and that causes the ticking rates of clocks to dilate. The flat spacetime paradigm is fully equivalent to the curved spacetime paradigm in that they both represent the same physical phenomena. However, their mathematical formulations are entirely different. Working physicists routinely switch between using curved and flat spacetime techniques depending on the requirements of the problem. The flat spacetime paradigm turns out to be especially convenient when performing approximate calculations in weak fields. Hence, flat spacetime techniques will be used when solving gravitational wave problems, while curved spacetime techniques will be used in the analysis of space tunnel ( The time tunnel ) .
Outer space, or simply space, is the expanse that exists beyond the Earth and between celestial bodies. Outer space is not completely empty—it is a hard vacuum containing a low density of particles, predominantly a plasma of hydrogen and helium, as well as electromagnetic radiation, magnetic fields, neutrinos, dust, and cosmic rays. The baseline temperature of outer space, as set by the background radiation from the Big Bang, is 2.7 kelvins (−270.45 °C; −454.81 °F). The plasma between galaxies accounts for about half of the baryonic (ordinary) matter in the universe; it has a number density of less than one hydrogen atom per cubic metre and a temperature of millions of kelvins. Local concentrations of matter have condensed into stars and galaxies. Studies indicate that 90% of the mass in most galaxies is in an unknown form, called dark matter, which interacts with other matter through gravitational but not electromagnetic forces. Observations suggest that the majority of the mass-energy in the observable universe is dark energy, a type of vacuum energy that is poorly understood. Intergalactic space takes up most of the volume of the universe, but even galaxies and star systems consist almost entirely of empty space.
Outer space does not begin at a definite altitude above the Earth's surface. However, the Kármán line, an altitude of 100 km (62 mi) above sea level, is conventionally used as the start of outer space in space treaties and for aerospace records keeping. The framework for international space law was established by the Outer Space Treaty, which entered into force on 10 October 1967. This treaty precludes any claims of national sovereignty and permits all states to freely explore outer space. Despite the drafting of UN resolutions for the peaceful uses of outer space, anti-satellite weapons have been tested in Earth orbit.
Humans began the physical exploration of space during the 20th century with the advent of high-altitude balloon flights. This was followed by manned rocket flights and, then, manned Earth orbit, first achieved by Yuri Gagarin of the Soviet Union in 1961. Due to the high cost of getting into space, manned spaceflight has been limited to low Earth orbit and the Moon. On the other hand, unmanned spacecraft have reached all of the known planets in the Solar System.
Outer space represents a challenging environment for human exploration because of the hazards of vacuum and radiation. Microgravity also has a negative effect on human physiology that causes both muscle atrophy and bone loss. In addition to these health and environmental issues, the economic cost of putting objects, including humans, into space is very high.
Outer space, or simply space, is the expanse that exists beyond the Earth and between celestial bodies. Outer space is not completely empty—it is a hard vacuum containing a low density of particles, predominantly a plasma of hydrogen and helium, as well as electromagnetic radiation, magnetic fields, neutrinos, dust, and cosmic rays. The baseline temperature of outer space, as set by the background radiation from the Big Bang, is 2.7 kelvins (−270.45 °C; −454.81 °F). The plasma between galaxies accounts for about half of the baryonic (ordinary) matter in the universe; it has a number density of less than one hydrogen atom per cubic metre and a temperature of millions of kelvins. Local concentrations of matter have condensed into stars and galaxies. Studies indicate that 90% of the mass in most galaxies is in an unknown form, called dark matter, which interacts with other matter through gravitational but not electromagnetic forces. Observations suggest that the majority of the mass-energy in the observable universe is dark energy, a type of vacuum energy that is poorly understood. Intergalactic space takes up most of the volume of the universe, but even galaxies and star systems consist almost entirely of empty space.
Outer space does not begin at a definite altitude above the Earth's surface. However, the Kármán line, an altitude of 100 km (62 mi) above sea level is conventionally used as the start of outer space in space treaties and for aerospace records keeping. The framework for international space law was established by the Outer Space Treaty, which entered into force on 10 October 1967. This treaty precludes any claims of national sovereignty and permits all states to freely explore outer space. Despite the drafting of UN resolutions for the peaceful uses of outer space, anti-satellite weapons have been tested in Earth orbit.
Humans began the physical exploration of space during the 20th century with the advent of high-altitude balloon flights. This was followed by manned rocket flights and, then, manned Earth orbit, first achieved by Yuri Gagarin of the Soviet Union in 1961. Due to the high cost of getting into space, manned spaceflight has been limited to low Earth orbit and the Moon. On the other hand, unmanned spacecraft have reached all of the known planets in the Solar System.
Outer space represents a challenging environment for human exploration because of the hazards of vacuum and radiation. Microgravity also has a negative effect on human physiology that causes both muscle atrophy and bone loss. In addition to these health and environmental issues, the economic cost of putting objects, including humans, into space is very high.
Interplanetary space
The sparse plasma (blue) and dust (white) in the tail of comet Hale–Bopp are being shaped by pressure from solar radiation and the solar wind, respectively
The volume of interplanetary space is a nearly total vacuum, with a mean free path of about one astronomical unit at the orbital distance of the Earth. However, this space is not completely empty, and is sparsely filled with cosmic rays, which include ionized atomic nuclei and various subatomic particles. There is also gas, plasma and dust, small meteors, and several dozen types of organic molecules discovered to date by microwave spectroscopy.A cloud of interplanetary dust is visible at night as a faint band called the zodiacal light.
Interplanetary space contains the magnetic field generated by the Sun. There are also magnetospheres generated by planets such as Jupiter, Saturn, Mercury and the Earth that have their own magnetic fields. These are shaped by the influence of the solar wind into the approximation of a teardrop shape, with the long tail extending outward behind the planet. These magnetic fields can trap particles from the solar wind and other sources, creating belts of charged particles such as the Van Allen radiation belts. Planets without magnetic fields, such as Mars, have their atmospheres gradually eroded by the solar wind.
Interstellar space
Bow shock formed by the magnetosphere of the young star LL Orionis (center) as it collides with the Orion Nebula flow
A number of molecules exist in interstellar space, as can tiny 0.1 μm dust particles. The tally of molecules discovered through radio astronomy is steadily increasing at the rate of about four new species per year. Large regions of higher density matter known as molecular clouds allow chemical reactions to occur, including the formation of organic polyatomic species. Much of this chemistry is driven by collisions. Energetic cosmic rays penetrate the cold, dense clouds and ionize hydrogen and helium, resulting, for example, in the trihydrogen cation. An ionized helium atom can then split relatively abundant carbon monoxide to produce ionized carbon, which in turn can lead to organic chemical reactions.
The local interstellar medium is a region of space within 100 parsecs (pc) of the Sun, which is of interest both for its proximity and for its interaction with the Solar System. This volume nearly coincides with a region of space known as the Local Bubble, which is characterized by a lack of dense, cold clouds. It forms a cavity in the Orion Arm of the Milky Way galaxy, with dense molecular clouds lying along the borders, such as those in the constellations of Ophiuchus and Taurus. (The actual distance to the border of this cavity varies from 60 to 250 pc or more.) This volume contains about 104–105 stars and the local interstellar gas counterbalances the astrospheres that surround these stars, with the volume of each sphere varying depending on the local density of the interstellar medium. The Local Bubble contains dozens of warm interstellar clouds with temperatures of up to 7,000 K and radii of 0.5–5 pc.
When stars are moving at sufficiently high peculiar velocities, their astrospheres can generate bow shocks as they collide with the interstellar medium. For decades it was assumed that the Sun had a bow shock. In 2012, data from Interstellar Boundary Explorer (IBEX) and NASA's Voyager probes showed that the Sun's bow shock does not exist. Instead, these authors argue that a subsonic bow wave defines the transition from the solar wind flow to the interstellar medium . A bow shock is the third boundary of an astrosphere after the termination shock and the astropause (called the heliopause in the Solar System).
Intergalactic space
A star-forming region in the Large Magellanic Cloud, perhaps the closest Galaxy to Earth's Milky Way
Surrounding and stretching between galaxies, there is a rarefied plasma that is organized in a galactic filamentary structure. This material is called the intergalactic medium (IGM). The density of the IGM is 5–200 times the average density of the Universe. It consists mostly of ionized hydrogen; i.e. a plasma consisting of equal numbers of electrons and protons. As gas falls into the intergalactic medium from the voids, it heats up to temperatures of 105 K to 107 K, which is high enough so that collisions between atoms have enough energy to cause the bound electrons to escape from the hydrogen nuclei; this is why the IGM is ionized. At these temperatures, it is called the warm–hot intergalactic medium (WHIM). (Although the plasma is very hot by terrestrial standards, 105 K is often called "warm" in astrophysics.) Computer simulations and observations indicate that up to half of the atomic matter in the Universe might exist in this warm–hot, rarefied state. When gas falls from the filamentary structures of the WHIM into the galaxy clusters at the intersections of the cosmic filaments, it can heat up even more, reaching temperatures of 108 K and above in the so-called intracluster medium (ICM)
____________________________________________________________________________________________________
AXIS IN PROCESSING TIME FOR GOING TO TIME TRAVEL
axis, time, and time travel is a curved line of time travel vibrations such as time channels in the form of spirals or longitudinal waves and transverse waves where longitudinal as a time tunnel and we and our spacecraft as transverse waves that enter the current of longitudinal waves .
Relativity and Time Travel
An elementary primer for a study of the actual physics of time travel.
For to sketch how both forward and backward time travel are permitted by relativity theory. The prospects of forward time travel are less complex to describe and will require fewer idealizations. Backwards time travel is much more a matter of purely theoretical consideration. After a brief introduction to relativity theory, we will describe a case of time travel to the future and a case of time travel to the past; each case is consistent with the laws of relativity theory.
Relativity and Minkowski Spacetime
In 1895, H. G. Wells penned a depiction of machine-based time travel as a serial later republished as a novella: The Time Machine. In it, Wells’ main character proposes that the universe includes not just three dimensions of space, but also a fourth of time. With the advent of Einstein’s Special Theory of Relativity in 1905 and the General Theory of Relativity in 1916, space and time were ultimately intertwined in effect making scientific a bit of what Wells imagined.It is a common practice to start discussions of relativity theory by introducing the idea of a frame of reference. We are brought up understanding space and time, in part, through our ordinary ways of measuring spatial properties like length (e.g., using meter sticks, tape measures, odometers, sonar, lasers, …) and temporal properties like duration (e.g., using sundials, calendars, stopwatches, atomic clocks, …). Employing frames of reference allows one to begin thinking about relativity theory using these familiar ways of making observations about space and time. Taking such an approach leads one quickly to conclusions that show that the resulting measurements are not absolute, but are relative to a frame of reference. Length and duration turn out to be frame-dependent.
Relativity theory, however, is a theory about the nature of the universe, and is not—in the first instance—about frames of reference. Indeed, when it comes to the possibility of time travel, frame-relative measurements are—conveniently for us—pretty incidental. Insofar as the laws of relativity do permit time travel, time travel turns out to be a frame-independent phenomenon. In order to present our examples of time travel, we will introduce a coordinate system for a particular frame of reference, but we do so only to allow a simple algebraic description of the key frame-independent phenomenon. In Minkowski Spacetime, the spacetime of the Special Theory of Relativity, the time measured or experienced by a person or object moving inertially between two events is proportional to the spacetime interval between the events. The spacetime interval between two events is frame-independent.
In Euclidean 3-Space, described using Cartesian coordinates, the interval between two points, (x2, y2, z2) and (x1, y1, z1) is defined as the square root of the sum of the squares of the separation between the points along the three spatial dimensions:
This separation between two points is the same no matter the choice of the origin or any rotation of the axes for the coordinate system; this is a defining feature of Cartesian coordinate systems.
To describe the separation between events in Minkowski Spacetime, we’ll use Lorentz coordinates. The location of a point is provided by an ordered four-tuple of coordinates, each along one of four dimensions. The interval between two points, (t2, x2, y2, z2) and (t1,x1, y1, z1), is not given by the separation for Euclidean 4-Space:
It is given by:
This interval formula is the chosen formula for the separation
between two events in Minkowski spacetime. The interval value between
two points holds no matter the choice of the origin or any rotation of
the axes of the coordinate system; this is a defining feature of Lorentz
coordinate systems.The spacetime interval, DM, given by the equation displayed above has physical significance. The interval is proportional to the amount of time that would be measured by a clock traveling along an inertial path between events located at (t2, x2, y2, z2) and (t1, x1, y1, z1).1 Observers in different frames of reference, using a Lorentz coordinate system with a different origin or a different orientation of the axes, may disagree about the separation of the events along the t-axis, the x-axis, the y-axis, or the z-axis, but not about the spacetime interval between the events. The correlation between the spacetime interval between two events and the time elapsed along the inertial path between them has been experimentally confirmed in numerous ways. We will mention a couple of these ways below.
A Trip to the Future
In order to present a case of forward time travel, we shall describe a simple example set in Minkowski spacetime. Suppose there is a civilization on a planet that includes events at (0, 0, 0, 0) and (10, 0, 0, 0), and at all the intermediate points between these two events along the t-axis of this Lorentz coordinate system. If Tim wants to time travel to the future to witness an event at (10, 0, 0 ,0), and if he wants to do it much sooner than the rest of his civilization, then Tim should take a different route through spacetime from (0, 0, 0, 0) to (10, 0, 0, 0) than does his civilization.To make the case a little more concrete, we assume that the separation on the t-axis between the two events corresponds to 10 years. Suppose that Tim travels away from the planet at a very high speed arriving at a nearby star at (5, 4, 0, 0). Take him to be traveling 4 light years along the x-axis and 5 years along the t-axis. Leaving immediately upon arrival at the star, Tim heads back to the planet, arriving back at the planet at (10, 0, 0, 0). So, Tim’s departure is at (0, 0, 0, 0). He travels at 80% of the speed of light, taking only five years to go 4 light years in the positive x direction. Then Tim travels at 80% of the speed of light, taking five years to travel 4 light years in the negative x direction, arriving home at (10, 0, 0, 0).
As we will see once we complete some easy calculations, one shouldn’t take diagrams like the one above too seriously. It turns out that the sum of the spacetime interval from (0, 0, 0, 0) to (5, 4, 0, 0) and the interval from (5, 4, 0, 0) to (10, 0, 0, 0) is less than the interval from (0, 0, 0, 0) to (10, 0, 0, 0). This clearly is not in line with the spatial distances we see between the coordinates and the figures depicting these points in the diagram!
An application of the spacetime interval formula reveals that time passes differently for Tim than it does for his civilization. The spacetime interval between (10, 0, 0, 0) and (0, 0, 0, 0) along the path of his home planet is given by:
Checking the two intervals that make up Tim’s trip, we get:
So, 40% less time has elapsed for Tim than has passed for his friends who stayed put on the planet. If 10 years have elapsed on the planet, then only 6 years have passed for Tim. Had he traveled at even higher speeds to and from the star, he could have gotten back in even less time. He could have witnessed the event at (10, 0, 0, 0) at an even younger age.
This is not just theory. The consequence of taking different paths through spacetime on the amount of time that passes has been observed and documented often. In one of the more famous experiments, completed in 1971, scientists J.C. Hafele and Richard E. Keating placed cesium beam clocks aboard a commercial airliner headed eastward around the world. The plane was flown around the world and then compared with a reference atomic time scale at rest. Upon completion of the trip, it was found that the clocks from the flight were about 59 nanoseconds behind the clock at rest, which is almost the exact value that relativity theory predicts. Confirmation also comes from the behavior of basic particles called muons. They have a short half-life—less than two microseconds. When moving at high speeds, muons survive much longer than this short half-life would lead us to expect. With higher speeds, the particles survive longer, because they have experienced less time. For additional discussion of these and other results, see Gott (2001, p. 36), Greene (2004, p. 449), and Pickover (1998, pp. 119-121).
Has Tim time-traveled to the future? Frank Arntzenius reports being unsure about there being a clear notion of forward time travel. He downplays the interest of trips like Tim’s:
According to (special and general) relativity two clocks that travel along different world-lines from spacetime point A to spacetime point B will, almost always, measure different time intervals between A and B no matter what the structure the spacetime has … So, on a fairly natural characterization of what it is for there to be forwards time travel, forwards time travel would be ubiquitous, too ubiquitous to be interesting
Others might worry that, really, time merely slows for Tim—that he doesn’t really time travel. Still others might worry that this couldn’t be time travel because the method described includes no way for Tim to travel back to the past.
We are sympathetic with Phil Dowe’s assessment of trips like Tim’s: “This is time travel by any reasonable definition” (p. 443). (Also see Horwich 1975, p. 432.) We are so for the following reasons: In some ways, Tim’s trip is like the trip the astronauts take in Planet of the Apes (1968), who unbeknownst to them make a round trip to Earth of the distant future. In some ways, Tim is like Marygay of The Forever War who purchases a cruiser to use as a time machine (p. 264) to meet up in a timely fashion with William, who is not expected to return from battle for at least two centuries of Earth time. Perhaps, it would be clearer that Tim was time traveling had we constructed our example so that Tim’s trip took even less time for him. Wells’s time traveler and the time travelers in most sci-fi plots cover days, years, or even centuries in a matter of seconds. That could have been done in our example by having Tim travel along a different path.
Admittedly, it would be truer to standard time travel plots if Tim could just as easily travel back to the past via a similar method; this aspect of Tim’s situation does not match with one natural preconception prompted by science fiction. But it should hardly be a surprise that, when we turn our attention from a concept born and initially revealed in science fiction to looking for instances of the concept in the pages of science, that we find some divergence. We should respect science-fiction informed thoughts about what time travel is like, but we should not demand that they all apply in order to reasonably classify a scientific phenomenon as time travel. Not all preconceptions of a phenomenon are required to be met for there to be an actual discovery of the phenomenon. Tim’s is a case of time travel to the future.
A Trip to the Past
Relativity theory also allows for ways to travel to the past. Because it connects nicely with our discussion above of Tim’s trip to the future, we will consider a form of backwards time travel associated with the work of physicist Kip Thorne, which also provides another manner of travel to the future. What we need is a wormhole time machine.To understand what a wormhole is, think about a tunnel through a mountain. Without the tunnel, we would have to travel around or over the mountain. With the tunnel, we could get to the other side much more quickly and easily, traveling a much shorter distance. Similarly, wormholes connect more ordinary regions of spacetime, thus permitting a shortcut between them. Of course, a tunnel through a mountain is not a time machine into the past. Neither, necessarily, is a wormhole.
Thorne and his colleagues described a method for turning a wormhole into a time machine. There are lots of obstacles. For example, you must first find a wormhole—and so far no one has. The wormhole has also got to be large enough (or be made large enough) for your body to fit through. You also better make sure that the wormhole will not collapse before you are done with your trip. Thorne and his colleagues describe possible methods for doing all this—none easy to put in place—but we will not concern ourselves with these practical details. For us, the focus will be on what Thorne has to say about how the nature of the spacetime permits one end of the wormhole to be later in time than the other end, thus providing a gateway to and from earlier times.
To do so, we are going to simplify in one significant way. Minkowski Spacetime does not include wormholes. We would need to go beyond the Special Theory of Relativity to consider the General Theory of Relativity in order to describe a spacetime that allows for wormholes. That, in turn, would require us to bring in more difficult math than would be appropriate for this discussion. Instead, think of us as working in with a spacetime that’s just like Minkowski Spacetime except for the wormhole and its immediate vicinity. With this simplification, the characteristic of spacetime that permits one to turn a wormhole into a wormhole time machine is easy to describe. In fact, we have already covered most of what you need to know.
To build our wormhole time machine, we just need to separate the mouths of a wormhole in time. So, let’s have Tim take one mouth of a wormhole connecting two spatial regions on his home planet with him on his trip to the star. (How does he manage that? Never you mind! That’s another one of those practical details that we are skipping over.)
The time it takes for one to travel through the wormhole need not change no matter how far apart in ordinary spacetime the mouths are, but the wormhole mouth traveling with Tim ages more slowly than does Tim’s civilization and the mouth of the wormhole left behind there. In keeping with our earlier example, when Tim arrives back at (10, 0, 0, 0), only 6 years have passed for Tim though 10 years have passed for his civilization. There is the same difference in the time that has passed for the two wormhole ends that end being located at (10, 0, 0, 0).
In the diagram above, though the two mouths of the wormhole are the same age at (0, 0, 0, 0), at (10, 0, 0, 0), the tan end of the wormhole is 4 years older than the gray end.
With no change in the length of the wormhole, the two mouths of the wormhole will stay in sync: Tom, a friend of Tim’s, could be watching Tim through the tan mouth of the wormhole, and there need not be any discrepancy between Tom’s watch and Tim’s watch. At any point during the trip, Tim could have hopped in the gray mouth, immediately exited the tan mouth, and Tim and Tom would agree about how much time had passed since Tim started his trip. Similarly, Tom could have hopped in the tan mouth of the wormhole, exited the gray mouth, and the two friends would agree about how much time had passed.
So, what happens if Tom hops into the tan entrance of the wormhole at (6, 0, 0, 0)? Because the ends of the wormhole are in sync, he would end up where and when 6 years had passed for Tim. So, he would immediately exit at (10, 0, 0, 0), thus using the wormhole time machine to take a trip four years into the future of his civilization! The other direction is available too. Tim could jump into the gray mouth of the wormhole he’s brought with him on his trip, hopping in at (10, 0, 0, 0), and time travel four years into the past of his civilization. If Tim wants to make a bundle of money once he is back four years in time, he should stop at a library and make note of some winning lottery numbers from three or four years earlier before entering the wormhole!
Conclusion
That is our introductory case for the conclusion that forward time travel and backward time travel are consistent with the theory of relativity. In fact, we have described two different methods for traveling to the future: (i) traveling along a different (shorter) path through spacetime than the rest of your civilization, or (ii) hopping in the earlier end of a wormhole time machine that connects two points in the history of your civilization. The wormhole time machine provides our only case of time travel to the past: Tim’s hopping in the later mouth of the wormhole connecting events in the history of his civilization. There are other possibilities permitted by relativity theory that provide for time travel to the future and time travel to the past. In Time Travel in Einstein’s Universe (Chapters 2 and 3), J. Richard Gott nicely describes some of these methods including a stay-at-home method of traveling to the future, a time tunnel time machine, and Gott’s own two-cosmic-strings method for traveling to the past.For those of you looking for a conclusive statement on whether the actual laws of nature permit time travel to the past, you’ll need to wait for a theory that goes beyond relativity theory, something like a finalized theory of quantum gravity. Thorne has recently provided an accessible sketch of his and other physicists’ doubts about whether the actual laws of nature do permit time travel in “Is Time Travel Allowed?” For those of you who are adventurous and feel ready to deal with some difficult physics, Smeenk and Wϋthrich’s “Time Travel and Time Machines” (2011) includes advanced discussion of whether time travel is permitted by our laws.
_________________________________________________________________________________
Gen . Mac Tech Look up (Jump Electronic Subject Input Internal Space Ellipse) JESI ISE loving 2 in 1 (Modern Human and Robo Humanoid) __ The function area in space and time goes outside of space and time which is invisible because we are moving toward the MACH (Moving Audio Combine Humanoid) and combine speed to WARP (Wing Angels Resources Planning)
________________________________________________________________________________




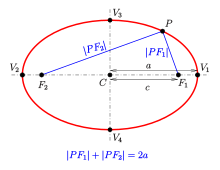
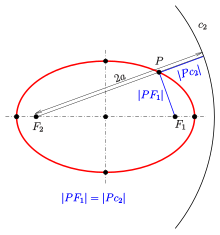
















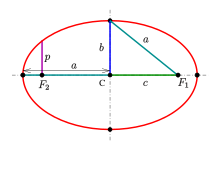






















































![{\displaystyle {\begin{aligned}a,b&={\frac {-{\sqrt {2{\Big (}AE^{2}+CD^{2}-BDE+(B^{2}-4AC)F{\Big )}\left((A+C)\pm {\sqrt {(A-C)^{2}+B^{2}}}\right)}}}{B^{2}-4AC}}\\x_{\circ }&={\frac {2CD-BE}{B^{2}-4AC}}\\[3pt]y_{\circ }&={\frac {2AE-BD}{B^{2}-4AC}}\\[3pt]\Theta &={\begin{cases}\arctan \left({\frac {1}{B}}\left(C-A-{\sqrt {(A-C)^{2}+B^{2}}}\right)\right)&{\text{for }}B\neq 0\\0&{\text{for }}B=0,\ A<C\\90^{\circ }&{\text{for }}B=0,\ A>C\\\end{cases}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f9bcbd931f81a6ed46cd1f02a499288f4f58a97)
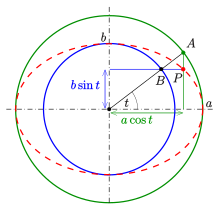








![{\displaystyle u\in [0,\,1],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c61b780db9ac550dd283876e16abe9c2cccdf8c3)







































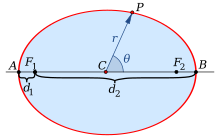


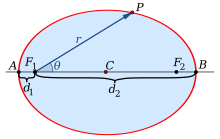





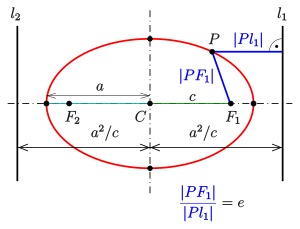


































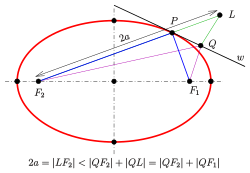
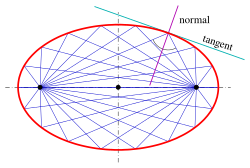












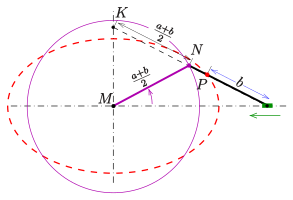





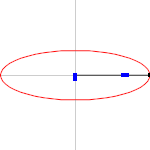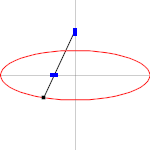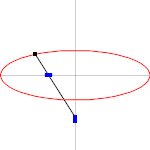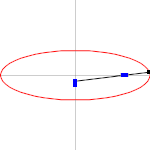

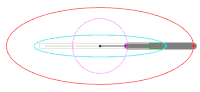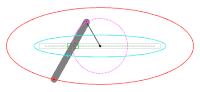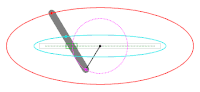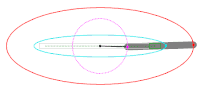
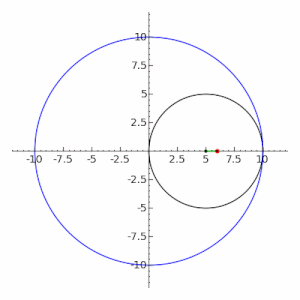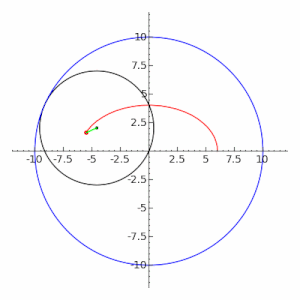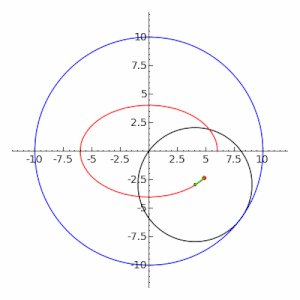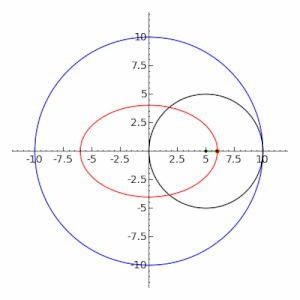









![{\displaystyle {\begin{aligned}a&={\frac {r_{a}+r_{p}}{2}}\\[2pt]b&={\sqrt {r_{a}r_{p}}}\\[2pt]\ell &={\frac {2}{{\frac {1}{r_{a}}}+{\frac {1}{r_{p}}}}}={\frac {2r_{a}r_{p}}{r_{a}+r_{p}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08835a73be73e7094f529d4eff42804930898271)



![{\displaystyle \mathrm {M} ={\sqrt {{\frac {2}{\gamma -1}}\left[\left({\frac {q_{c}}{p}}+1\right)^{\frac {\gamma -1}{\gamma }}-1\right]}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6cfb0b14f5726032a386928f8312725a3325c4c)



![{\displaystyle {\frac {p_{t}}{p}}=\left[{\frac {\gamma +1}{2}}\mathrm {M} ^{2}\right]^{\frac {\gamma }{\gamma -1}}\cdot \left[{\frac {\gamma +1}{1-\gamma +2\gamma \,\mathrm {M} ^{2}}}\right]^{\frac {1}{\gamma -1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e40925c7d73812aaeb7be0541fb045abfe268c54)