All life processes always begin and are initiated by the concept of attraction (Push and Pull), some of which are:
1. Love which is the attraction between men and women
towards the stability of body and soul.
2. energy conservation where the numerical value of energy moves in a manner
push - pull goes to neutral ie 0 (null or void) or
the harmonization process also leads to core stability although it can
into a different form but the taste is the same.
3. read and write memory and copy paste which is
Data collection (Push) also processes data into results
Legitimate information is a mechanism (Pull).
4. Push (collect) and delete (Pull).
5. electronic circuits which are also systems of attraction
where energy will turn into motion, light, indicators
and heat is also a magnet until such a function is stable
Batteries, batteries, adapters (there are harmonizations 1, 2, 3, 4 are called
ripple), electronic components and their circuit pathways.
6. Space is also a process of attraction of various kinds
kinds of harmonizing forces and energies that move in space
and time so that they experience emptiness or vacuum,
or we can call space is a neutral zone (0)
1. Love which is the attraction between men and women
towards the stability of body and soul.
2. energy conservation where the numerical value of energy moves in a manner
push - pull goes to neutral ie 0 (null or void) or
the harmonization process also leads to core stability although it can
into a different form but the taste is the same.
3. read and write memory and copy paste which is
Data collection (Push) also processes data into results
Legitimate information is a mechanism (Pull).
4. Push (collect) and delete (Pull).
5. electronic circuits which are also systems of attraction
where energy will turn into motion, light, indicators
and heat is also a magnet until such a function is stable
Batteries, batteries, adapters (there are harmonizations 1, 2, 3, 4 are called
ripple), electronic components and their circuit pathways.
6. Space is also a process of attraction of various kinds
kinds of harmonizing forces and energies that move in space
and time so that they experience emptiness or vacuum,
or we can call space is a neutral zone (0)
Gen. Mac Tech to operation and change operation
1
( AMNIMARJESLO SAN )
2
⇉ Push–pull Input / Output ⇇
A push–pull in electronic is a concept of attraction in electronics is a special concept because all electronic components function due to the attractive relationship between positive and negative electrons, as well as the attraction of photons in the electronic components of light. Thus humans in life there is also the process of attraction that is love.
electronic circuit
that uses a pair of active devices that alternately supply current to,
or absorb current from, a connected load. Push–pull outputs are present
in TTL and CMOS digital logic circuits and in some types of amplifiers, and are usually realized as a complementary pair of transistors, one dissipating or sinking current from the load to ground or a negative power supply, and the other supplying or sourcing current to the load from a positive power supply ,
Push–pull circuits are widely used in many amplifier output stages .
Push–pull transistor output stages :
Categories include:
Transformer-output transistor power amplifiers
It is now very rare to use output transformers with transistor amplifiers, although such amplifiers offer the best opportunity for matching the output devices (with only PNP or only NPN devices required).Totem pole push–pull output stages
Two matched transistors of the same polarity can be arranged to supply opposite halves of each cycle without the need for an output transformer, although in doing so the driver circuit often is asymmetric and one transistor will be used in a common-emitter configuration while the other is used as an emitter follower. This arrangement is less used today than during the 1970's; it can be implemented with few transistors (not so important today) but is relatively difficult to balance and to keep a low distortion.Symmetrical push–pull
Each half of the output pair "mirror" the other, in that an NPN (or N-Channel FET) device in one half will be matched by a PNP (or P-Channel FET) in the other. This type of arrangement tends to give lower distortion than quasi-symmetric stages because even harmonics are cancelled more effectively with greater symmetry.Quasi-symmetrical push–pull
In the past when good quality PNP complements for high power NPN silicon transistors were limited, a workaround was to use identical NPN output devices, but fed from complementary PNP and NPN driver circuits in such a way that the combination was close to being symmetrical (but never as good as having symmetry throughout). Distortion due to mismatched gain on each half of the cycle could be a significant problem.Super-symmetric output stages
Employing some duplication in the whole driver circuit, to allow symmetrical drive circuits can improve matching further, although driver asymmetry is a small fraction of the distortion generating process. Using a bridge-tied load arrangement allows a much greater degree of matching between positive and negative halves, compensating for the inevitable small differences between NPN and PNP devices.Square-law push–pull
The output devices, usually MOSFETs or vacuum tubes, are configured so that their square-law transfer characteristics (that generate second-harmonic distortion if used in a single-ended circuit) cancel distortion to a large extent. That is, as one transistor's gate-source voltage increases, the drive to the other device is reduced by the same amount and the drain (or plate) current change in the second device approximately corrects for the non-linearity in the increase of the first.Push–pull tube (valve) output stages
Vacuum tubes (valves) are not available in complementary types (as are pnp/npn transistors), so the tube push–pull amplifier has a pair of identical output tubes or groups of tubes with the control grids driven in antiphase. These tubes drive current through the two halves of the primary winding of a center-tapped output transformer. Signal currents add, while the distortion signals due to the non-linear characteristic curves of the tubes subtract. These amplifiers were first designed long before the development of solid-state electronic devices; they are still in use by both audiophiles and musicians who consider them to sound better.Vacuum tube push–pull amplifiers usually use an output transformer, although Output-transformerless (OTL) tube stages exist (such as the SEPP/SRPP and the White Cathode Follower below). The phase-splitter stage is usually another vacuum tube but a transformer with a center-tapped secondary winding was occasionally used in some designs. Because these are essentially square-law devices, the comments regarding distortion cancellation mentioned above apply to most push–pull tube designs when operated in class A (i.e. neither device is driven to its non-conducting state).
A Single Ended Push–Pull (SEPP, SRPP or mu-follower) output stage, originally called the Series-Balanced amplifier (US patent 2,310,342, Feb 1943). is similar to a totem-pole arrangement for transistors in that two devices are in series between the power supply rails, but the input drive goes only to one of the devices, the bottom one of the pair; hence the (seemingly contradictory) Single-Ended description. The output is taken from the cathode of the top (not directly driven) device, which acts part way between a constant current source and a cathode follower but receiving some drive from the plate (anode) circuit of the bottom device. The drive to each tube therefore might not be equal, but the circuit tends to keep the current through the bottom device somewhat constant throughout the signal, increasing the power gain and reducing distortion compared with a true single-tube single-ended output stage.
The White Cathode Follower (Patent 2,358,428, Sep 1944 by E. L. C. White) is similar to the SEPP design above, but the signal input is to the top tube, acting as a cathode follower, but one where the bottom tube (in common cathode configuration) if fed (usually via a step-up transformer) from the current in the plate (anode) of the top device. It essentially reverses the roles of the two devices in SEPP. The bottom tube acts part way between a constant current sink and an equal partner in the push–pull workload. Again, the drive to each tube therefore might not be equal.
Transistor versions of the SEPP and White follower do exist, but are rare.
Ultra-linear push–pull
A so-called ultra-linear push–pull amplifier uses either pentodes or tetrodes with their screen grid fed from a percentage of the primary voltage on the output transformer. This gives efficiency and distortion that is a good compromise between triode (or triode-strapped) power amplifier circuits and conventional pentode or tetrode output circuits where the screen is fed from a relatively constant voltage source.Push–pull converter
A push–pull converter is a type of DC-to-DC converter, a switching converter that uses a transformer to change the voltage of a DC power supply. The distinguishing feature of a push-pull converter is that the transformer primary is supplied with current from the input line by pairs of transistors in a symmetrical push-pull circuit. The transistors are alternately switched on and off, periodically reversing the current in the transformer. Therefore, current is drawn from the line during both halves of the switching cycle. This contrasts with buck-boost converters, in which the input current is supplied by a single transistor which is switched on and off, so current is only drawn from the line during half the switching cycle. During the other half the output power is supplied by energy stored in inductors or capacitors in the power supply. Push–pull converters have steadier input current, create less noise on the input line, and are more efficient in higher power applications.
Push-pull converter (+12V → ±18V; 50W) as potted module. ① transformer; ② and ③ electrolytic capacitors vertical and horizontal mounted; ④ discrete circuit board in through-hole technology .
Circuit operation

Conceptual schematic of a full-bridge converter. This is not a center tapped or split primary push-pull converter.
Top: Simple inverter circuit shown with an electromechanical switch
and automatic equivalent
auto-switching device implemented with two transistors and split winding auto-transformer in place of the mechanical switch.
and automatic equivalent
auto-switching device implemented with two transistors and split winding auto-transformer in place of the mechanical switch.
In any case, the output is then rectified and sent to the load. Capacitors are often included at the output to filter the switching noise.
In practice, it is necessary to allow a small interval between powering the transformer one way and powering it the other: the “switches” are usually pairs of transistors (or similar devices), and were the two transistors in the pair to switch simultaneously there would be a risk of shorting out the power supply. Hence, a small wait is needed to avoid this problem. This wait time is called "Dead Time" and is necessary to avoid transistor shoot-through.
Transistors
N-type and P-type power transistors can be used. Power MOSFETs are often chosen for this role due to their high current switching capability and their inherently low ON resistance. The gates or bases of the power transistors are tied via a resistor to one of the supply voltages. A P-type transistor is used to pull up the N-type power transistor gate (common source) and an N-type transistor is used to pull down the P-type power transistor gate.Alternatively, all power transistors can be N-type, which offer around three times the gain of their P-type equivalents. In this alternative the N-type transistor used in place of the P-type has to be driven in this way: The voltage is amplified by one P-type transistor and one N-type transistor in common base configuration to rail-to-rail amplitude. Then the power transistor is driven in common drain configuration to amplify the current.
In high frequency applications both transistors are driven with common source.
The operation of the circuit means that both transistors are actually pushing, and the pulling is done by a low pass filter in general, and by a center tap of the transformer in the converter application. But because the transistors push in an alternating fashion, the device is called a push-pull converter.
Timing
If both transistors are in their on state, a short circuit results. On the other hand, if both transistors are in their off state, high voltage peaks appear due to back EMF.If the driver for the transistors is powerful and fast enough, the back EMF has no time to charge the capacity of the windings and of the body-diode of the MOSFETs to high voltages.
If a microcontroller is used, it can be used to measure the peak voltage and digitally adjust the timing for the transistors, so that the peak only just appears. This is especially useful when the transistors are starting from cold with no peaks, and are in their boot phase.
The cycle starts with no voltage and no current. Then one transistor turns on, a constant voltage is applied to the primary, current increases linearly, and a constant voltage is induced in the secondary. After some time T the transistor is turned off, the parasitic capacities of the transistors and the transformer and the inductance of the transformer form an LC circuit which swings to the opposite polarity. Then the other transistor turns on. For the same time T charge flows back into the storage capacitor, then changes the direction automatically, and for another time T the charge flows in the transformer. Then again the first transistor turns on until the current is stopped. Then the cycle is finished, another cycle can start anytime later. The S-shaped current is needed to improve over the simpler converters and deal efficiently with remanence.
3
⇉The conservation of energy on push - pull⇇
When you do a useful job with a force (a push or a pull), such as moving a car uphill, we say you're doing work, and that takes energy. ... So no energy is created or destroyed here: you're simply converting energy stored as fuel inside your body into potential energy stored by the car (because of its height).
Cars can pull off the same trick. Depending on which make and model you own, you probably know that it does so many kilometers or miles to the gallon; in other words, using a certain amount of energy-rich gasoline, it can transport you (and a moderate load) a certain distance down the road. What we have here are two examples of machines—the human body and the automobile—that obey one of the most important laws of physics: the conservation of energy. Written in its simplest form, it says that you can't create or destroy energy, but you can convert it from one form into another. Pretty much everything that happens in the universe obeys.
What is the conservation of energy?
The first thing we need to note is that the law of conservation of energy is completely different from energy conservation. Energy conservation means saving energy through such things as insulating your home or using public transportation; generally it saves you money and helps the planet. The conservation of energy has nothing to do with saving energy: it's all about where energy comes from and where it goes.Write the law formally and it sounds like this:
In a closed system, the amount of energy is fixed. You can't create any more energy inside the system or destroy any of the energy that's already in there. But you can convert the energy you have from one form to another (and sometimes back again).A "closed system" is a bit like a sealed box around whatever we're studying: no energy can leak into the box from the inside (or be introduced to the box from outside).
There are some even simpler, more familiar ways of stating the conservation of energy. "No pain, no gain" is a rough everyday equivalent: if you want something, you have to work for it. "There's no such thing as a free lunch" and "You don't get anything for free" are other examples.
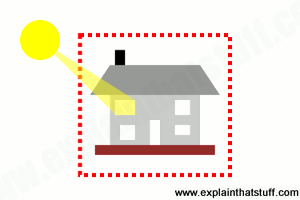
Artwork: This house is an example of a closed system: the energy that's inside the red dotted line stays as it is or gets converted into other forms. We can't create any new energy inside the house out of nothing at all, and we can't make energy inside the house vanish without trace, though we can turn it into other forms. So what if one room of the house suddenly starts getting hotter? The heat energy making that happen must be coming from energy that's already inside the house in a different form (maybe it's wood in a fire that's being burned to release the chemical energy locked inside it). If that's not the case, we don't have a closed system: the "extra" heat must be coming into the house from outside (maybe strong sunlight streaming in through the window).
Examples of the conservation of energy
The conservation of energy (and the idea of a "closed system") sounds a bit abstract, but it becomes an awful lot clearer when we consider some real-life examples.Driving a car
Fill a car up with gasoline and you have a closed system. All the energy you have at your disposal is locked inside the gas in your tank in chemical form. When the gas flows into your engine, it burns with oxygen in the air. The chemical energy in the gas is converted first into heat energy: the burning fuel makes hot expanding gas, which pushes the pistons in the engine cylinders. In this way, the heat is converted into mechanical energy. The pistons turn the crankshaft, gears, and driveshaft and—eventually—the car's wheels. As the wheels turn, they speed the vehicle along the road, giving it kinetic energy (energy of movement).If a car were 100 percent efficient, all the chemical energy originally locked inside the gasoline would be converted into kinetic energy. Unfortunately, energy is wasted at each stage of this process. Some is lost to friction when metal parts rub and wear against one another and heat up; some energy is lost as sound (cars can be quite noisy—and sound is energy that has to come from somewhere) Not all the energy the car produces moves you down the road: quite a lot has to push against the air (so it's lost to air resistance or drag), while some will be used to power things like the headlights, air conditioning, and so on. Nevertheless, if you measure the energy you start with (in the gasoline) and calculate how much energy you finish with and lose on the way (everything from useful kinetic energy and useless energy lost to friction, sound, air resistance, and so on), you'll find the energy account always balances: the energy you start with is the energy you finish with.
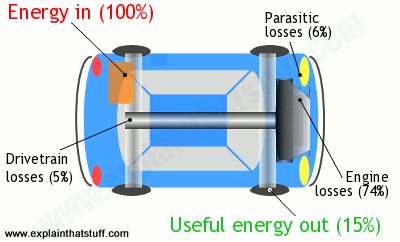
Artwork: Like everything else, cars must obey the law of conservation of energy. They convert the energy in fuel into mechanical energy that moves you down the road, but waste quite a lot of energy in the process. If you put 100 units of energy into a car (in the form of fuel), only 15 units or so move you down the road. The rest is wasted as heat losses in the engine (74 percent); parasitic losses (6%, making electricity, for example, to light the headlamps); and drivetrain losses (5%, sending power to the wheels). The 15 useful units of energy are used to overcome drag (air resistance), friction (in the brakes), and rolling resistance (in the tires). Every bit of energy we put into a car has to go somewhere, so the energy outputs (74% + 6% + 5% + 15%) must always exactly add up to the original energy input (100%). Figures for city driving from Where the energy goes, fueleconomy.gov.
Now this only applies if your car is a "closed system." If you're driving along the straight and the road suddenly starts going downhill, you're going to be able to go much further than you'd be able to go otherwise. Does this violate the conservation of energy? No, because we're no longer dealing with a closed system. Your car is gaining kinetic energy from the gasoline in its tank, but it's also gaining kinetic energy because it's going downhill. This isn't a closed system so the conservation of energy doesn't apply anymore.
Boiling a kettle

Photo: An electric kettle like this converts electrical energy into heat energy.
That's the reverse of the process that happens in the power plant that supplies your home, where electricity is produced using heat energy released by burning a fuel such as coal, oil, or gas.
Boil water with an electric kettle and you're seeing the conservation of energy at work again. Electrical energy drawn from the power outlet on your wall flows into the heating element in the base of your kettle. As the current flows through the element, the element rapidly heats up, so the electrical energy is converted into heat energy that gets passed to the cold water surrounding it. After a couple of minutes, the water boils and (if the power stays on) starts to turn to steam. How does the conservation of energy apply here? Most of the electrical energy that enters the kettle is converted into heat energy in the water, though some is used to provide latent heat of evaporation (the heat we need to give to liquids to turn them into gases such as steam). If you add up the total electrical energy "lost" by the electricity supply and the total energy gained by the water, you should find they're almost exactly the same. Why aren't they exactly equal? Simply because we don't have a closed system here. Some of the original energy is converted to sound and wasted (kettles can be quite noisy). Kettles also give off some heat to their surroundings—so that's also wasted energy.
Pushing a car uphill
In the everyday world, "work" is something you do to earn money; in physics, work has a different meaning. When you do a useful job with a force (a push or a pull), such as moving a car uphill, we say you're doing work, and that takes energy. If you push a car uphill, it has more potential energy at the top of the hill than it had at the bottom. Have you violated the conservation of energy by creating potential energy out of thin air?No! To push the car, you have to do work against the force of gravity. Your body has to use energy to do work. Most of the energy your body uses is gained by the car as you push it uphill. The energy your body loses is pretty much equal to the work it does against gravity. And the energy the car gains is the same as the work done. So no energy is created or destroyed here: you're simply converting energy stored as fuel inside your body into potential energy stored by the car (because of its height).
Who discovered the conservation of energy?
How do we know the conservation of energy is true? First, it sounds sensible. If you put a heavy log on a fire it might burn for an hour. If you put a second log, roughly the same size, on the fire, it's reasonable to suppose you'll get twice as much heat or the fire will burn twice as long. By the same token, if five bananas can supply your body with an hour's energy, ten bananas should keep you running for two hours—although you might not enjoy guzzling them all at once! In other words, the energy in (the logs you add to the fire or the bananas you eat) is equal to the energy out (the heat you get by burning logs or the energy you make by eating bananas).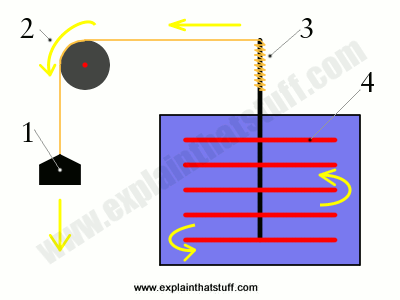
Photo: The Mechanical Equivalent of Heat: In James Prescott Joule's famous experiment, a falling weight (1) pulls on a rope that passes over a pulley (2). The rope spins an axle (3) that turns a paddle inside a sealed container of water (4). As the paddle spins, the water heats up. Joule proved that the heat energy gained by the water was exactly the same as the potential energy lost by the weight.
“... the quantity of heat produced by the friction of bodies, whether solid or liquid, is always proportional to the quantity of force expended.”
James Prescott Joule, The Mechanical Equivalent of Heat, 1845.
Joule built on earlier work by Anglo-American physicist Benjamin Thompson (1753–1814), also known as Count Rumford. While working in a Germany artillery factory, Rumford noted that cannon barrels got hot when they were being drilled out. He swiftly realized that the heat was not a magic property of the metal (as many people supposed) but came from the mechanical, frictional process of drilling: the more you drilled, the hotter the metal got. Rumford's simple calculations produced results that, according to Joule, were "not very widely different from that which I have deduced from my own experiments." That was a sign both men were on the right track.
Why perpetual motion machines never work
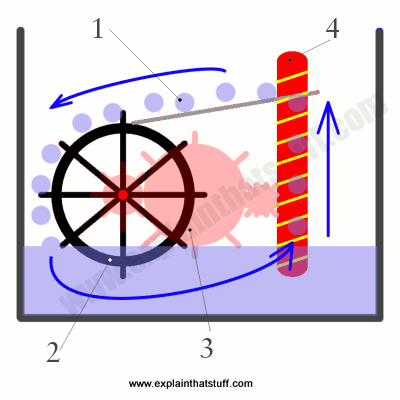
Back in the 19th century, charlatan inventors would pop up from time to time showing off miracle machines that seemed to be able to drive themselves forever. Inventions like this are called perpetual motion machines: they seem to be able to move forever without anyone adding any more energy. Often, machines like this were blatant tricks: the mechanisms were powered by a concealed assistant who sat in the shadows turning a hidden handle! Some of the machines sound plausible, but all of them unfortunately fall foul of the conservation of energy.
In one version of perpetual motion, illustrated here, water (1) tips down onto a waterwheel, turning it around (2). The turning wheel drives gears (3) that power an Archimedes screw, which lifts the water back up to the top, theoretically allowing the whole cycle to repeat itself forever. Although you might think energy is being recycled as the water moves around, it's also being lost all the time. The water at the top has potential energy and that can indeed drive a waterwheel as it falls. But some energy will be lost to friction as the wheel turns. More energy will be lost to friction in the gears and the screw. So, between them, the wheel, gears, and screw will not have the same amount of energy as the potential energy the water lost originally. That means the screw cannot lift as as much water back to the bath as fell down from it originally—so the machine will very quickly come to a stop.
What about the conservation of mass?
Nuclear reactions seem to create energy out of nothing breaking up or joining together atoms. Do they violate the conservation of energy? No!Albert Einstein's famous equation E=mc2 shows that energy and mass are different forms of the same thing. Loosely speaking, you can convert a small amount of mass into a large amount of energy (as in a nuclear power plant, where large atoms split apart and give off energy in the process). Einstein's equation shows us we sometimes need to factor mass into the conservation of energy. In a nuclear reaction, we start off with one set of atoms (a certain amount of energy in the form of mass) and end up with a different set of atoms (a different amount of energy locked in their mass) plus energy that's released as heat. If we factor in the mass of the atoms before and after the reaction, plus the energy released in the process, we find the conservation of energy is satisfied exactly. Since mass is a form of energy, it's clear that we can't destroy mass or create it out of nothing in the same way that we can't create or destroy energy.
4
⇉Push vs. pull: data movement for linked data structures⇇
As the performance gap between the CPU and main memory continues to grow, techniques to hide memory latency are essential to deliver a high performance computer system. Prefetching can often overlap memory latency with computation for array-based numeric applications. However, prefetching for pointer-intensive applications still remains a challenging problem. Prefetching linked data structures (LDS) is difficult because the address sequence of LDS traversal does not present the same arithmetic regularity as array-based applications and the data dependence of pointer dereferences can serialize the address generation process.
hardware/software mechanism to reduce memory access latencies for linked data structures. Instead of relying on the past address history to predict future accesses, we identify the load instructions that traverse the LDS, and execute them ahead of the actual computation. To overcome the serial nature of the LDS address generation, we attach a prefetch controller to each level of the memory hierarchy and push, rather than pull, data to the CPU.
Stack (abstract data type)
In computer science, a stack is an abstract data type that serves as a collection of elements, with two principal operations:
- push, which adds an element to the collection, and
- pop, which removes the most recently added element that was not yet removed.
Considered as a linear data structure, or more abstractly a sequential collection, the push and pop operations occur only at one end of the structure, referred to as the top of the stack. This makes it possible to implement a stack as a singly linked list and a pointer to the top element. A stack may be implemented to have a bounded capacity. If the stack is full and does not contain enough space to accept an entity to be pushed, the stack is then considered to be in an overflow state. The pop operation removes an item from the top of the stack.
A stack is needed to implement depth-first search.

Similar to a stack of plates, adding or removing is only possible at the top

Simple representation of a stack runtime with push and pop operations.
Hardware stack
A common use of stacks at the architecture level is as a means of allocating and accessing memory.Basic architecture of a stack
A typical stack, storing local data and call information for nested procedure calls (not necessarily nested procedures). This stack grows downward from its origin. The stack pointer points to the current topmost datum
on the stack. A push operation decrements the pointer and copies the
data to the stack; a pop operation copies data from the stack and then
increments the pointer. Each procedure called in the program stores
procedure return information (in yellow) and local data (in other
colors) by pushing them onto the stack. This type of stack
implementation is extremely common, but it is vulnerable to buffer overflow attacks (see the text).
The two operations applicable to all stacks are:
- a push operation, in which a data item is placed at the location pointed to by the stack pointer, and the address in the stack pointer is adjusted by the size of the data item;
- a pop or pull operation: a data item at the current location pointed to by the stack pointer is removed, and the stack pointer is adjusted by the size of the data item.
Stack pointers may point to the origin of a stack or to a limited range of addresses either above or below the origin (depending on the direction in which the stack grows); however, the stack pointer cannot cross the origin of the stack. In other words, if the origin of the stack is at address 1000 and the stack grows downwards (towards addresses 999, 998, and so on), the stack pointer must never be incremented beyond 1000 (to 1001, 1002, etc.). If a pop operation on the stack causes the stack pointer to move past the origin of the stack, a stack underflow occurs. If a push operation causes the stack pointer to increment or decrement beyond the maximum extent of the stack, a stack overflow occurs.
Some environments that rely heavily on stacks may provide additional operations, for example:
- Duplicate: the top item is popped, and then pushed again (twice), so that an additional copy of the former top item is now on top, with the original below it.
- Peek: the topmost item is inspected (or returned), but the stack pointer and stack size does not change (meaning the item remains on the stack). This is also called top operation in many articles.
- Swap or exchange: the two topmost items on the stack exchange places.
- Rotate (or Roll): the n topmost items are moved on the stack in a rotating fashion. For example, if n=3, items 1, 2, and 3 on the stack are moved to positions 2, 3, and 1 on the stack, respectively. Many variants of this operation are possible, with the most common being called left rotate and right rotate.
A right rotate will move the first element to the third position, the second to the first and the third to the second. Here are two equivalent visualizations of this process:
apple banana banana ===right rotate==> cucumber cucumber apple
cucumber apple banana ===left rotate==> cucumber apple bananaA stack is usually represented in computers by a block of memory cells, with the "bottom" at a fixed location, and the stack pointer holding the address of the current "top" cell in the stack. The top and bottom terminology are used irrespective of whether the stack actually grows towards lower memory addresses or towards higher memory addresses.
Pushing an item on to the stack adjusts the stack pointer by the size of the item (either decrementing or incrementing, depending on the direction in which the stack grows in memory), pointing it to the next cell, and copies the new top item to the stack area. Depending again on the exact implementation, at the end of a push operation, the stack pointer may point to the next unused location in the stack, or it may point to the topmost item in the stack. If the stack points to the current topmost item, the stack pointer will be updated before a new item is pushed onto the stack; if it points to the next available location in the stack, it will be updated after the new item is pushed onto the stack.
Popping the stack is simply the inverse of pushing. The topmost item in the stack is removed and the stack pointer is updated, in the opposite order of that used in the push operation.
Stack in main memory
Many CISC-type CPU designs, including the x86, Z80 and 6502, have a dedicated register for use as the call stack stack pointer with dedicated call, return, push, and pop instructions that implicitly update the dedicated register, thus increasing code density. Some CISC processors, like the PDP-11 and the 68000, also have special addressing modes for implementation of stacks, typically with a semi-dedicated stack pointer as well (such as A7 in the 68000). In contrast, most RISC CPU designs do not have dedicated stack instructions and therefore most if not all registers may be used as stack pointers as needed.Stack in registers or dedicated memory
The x87 floating point architecture is an example of a set of registers organised as a stack where direct access to individual registers (relative the current top) is also possible. As with stack-based machines in general, having the top-of-stack as an implicit argument allows for a small machine code footprint with a good usage of bus bandwidth and code caches, but it also prevents some types of optimizations possible on processors permitting random access to the register file for all (two or three) operands. A stack structure also makes superscalar implementations with register renaming (for speculative execution) somewhat more complex to implement, although it is still feasible, as exemplified by modern x87 implementations.Sun SPARC, AMD Am29000, and Intel i960 are all examples of architectures using register windows within a register-stack as another strategy to avoid the use of slow main memory for function arguments and return values.
There are also a number of small microprocessors that implements a stack directly in hardware and some microcontrollers have a fixed-depth stack that is not directly accessible. Examples are the PIC microcontrollers, the Computer Cowboys MuP21, the Harris RTX line, and the Novix NC4016. Many stack-based microprocessors were used to implement the programming language Forth at the microcode level. Stacks were also used as a basis of a number of mainframes and mini computers. Such machines were called stack machines, the most famous being the Burroughs B5000.
Applications of stacks
Expression evaluation and syntax parsing
Calculators employing reverse Polish notation use a stack structure to hold values. Expressions can be represented in prefix, postfix or infix notations and conversion from one form to another may be accomplished using a stack. Many compilers use a stack for parsing the syntax of expressions, program blocks etc. before translating into low level code. Most programming languages are context-free languages, allowing them to be parsed with stack based machines.Backtracking
Another important application of stacks is backtracking. Consider a simple example of finding the correct path in a maze. There are a series of points, from the starting point to the destination. We start from one point. To reach the final destination, there are several paths. Suppose we choose a random path. After following a certain path, we realise that the path we have chosen is wrong. So we need to find a way by which we can return to the beginning of that path. This can be done with the use of stacks. With the help of stacks, we remember the point where we have reached. This is done by pushing that point into the stack. In case we end up on the wrong path, we can pop the last point from the stack and thus return to the last point and continue our quest to find the right path. This is called backtracking.The prototypical example of a backtracking algorithm is depth-first search, which finds all vertices of a graph that can be reached from a specified starting vertex. Other applications of backtracking involve searching through spaces that represent potential solutions to an optimization problem. Branch and bound is a technique for performing such backtracking searches without exhaustively searching all of the potential solutions in such a space.
Compile time memory management
A number of programming languages are stack-oriented, meaning they define most basic operations (adding two numbers, printing a character) as taking their arguments from the stack, and placing any return values back on the stack. For example, PostScript has a return stack and an operand stack, and also has a graphics state stack and a dictionary stack. Many virtual machines are also stack-oriented, including the p-code machine and the Java Virtual Machine.Almost all calling conventions—the ways in which subroutines receive their parameters and return results—use a special stack (the "call stack") to hold information about procedure/function calling and nesting in order to switch to the context of the called function and restore to the caller function when the calling finishes. The functions follow a runtime protocol between caller and callee to save arguments and return value on the stack. Stacks are an important way of supporting nested or recursive function calls. This type of stack is used implicitly by the compiler to support CALL and RETURN statements (or their equivalents) and is not manipulated directly by the programmer.
Some programming languages use the stack to store data that is local to a procedure. Space for local data items is allocated from the stack when the procedure is entered, and is deallocated when the procedure exits. The C programming language is typically implemented in this way. Using the same stack for both data and procedure calls has important security implications (see below) of which a programmer must be aware in order to avoid introducing serious security bugs into a program.
Efficient algorithms
Several algorithms use a stack (separate from the usual function call stack of most programming languages) as the principle data structure with which they organize their information. These include:- Graham scan, an algorithm for the convex hull of a two-dimensional system of points. A convex hull of a subset of the input is maintained in a stack, which is used to find and remove concavities in the boundary when a new point is added to the hull.
- Part of the SMAWK algorithm for finding the row minima of a monotone matrix uses stacks in a similar way to Graham scan.
- All nearest smaller values, the problem of finding, for each number in an array, the closest preceding number that is smaller than it. One algorithm for this problem uses a stack to maintain a collection of candidates for the nearest smaller value. For each position in the array, the stack is popped until a smaller value is found on its top, and then the value in the new position is pushed onto the stack.
- The nearest-neighbor chain algorithm, a method for agglomerative hierarchical clustering based on maintaining a stack of clusters, each of which is the nearest neighbor of its predecessor on the stack. When this method finds a pair of clusters that are mutual nearest neighbors, they are popped and merged.
Security
Some computing environments use stacks in ways that may make them vulnerable to security breaches and attacks. Programmers working in such environments must take special care to avoid the pitfalls of these implementations.For example, some programming languages use a common stack to store both data local to a called procedure and the linking information that allows the procedure to return to its caller. This means that the program moves data into and out of the same stack that contains critical return addresses for the procedure calls. If data is moved to the wrong location on the stack, or an oversized data item is moved to a stack location that is not large enough to contain it, return information for procedure calls may be corrupted, causing the program to fail.
Malicious parties may attempt a stack smashing attack that takes advantage of this type of implementation by providing oversized data input to a program that does not check the length of input. Such a program may copy the data in its entirety to a location on the stack, and in so doing it may change the return addresses for procedures that have called it. An attacker can experiment to find a specific type of data that can be provided to such a program such that the return address of the current procedure is reset to point to an area within the stack itself (and within the data provided by the attacker), which in turn contains instructions that carry out unauthorized operations.
This type of attack is a variation on the buffer overflow attack and is an extremely frequent source of security breaches in software, mainly because some of the most popular compilers use a shared stack for both data and procedure calls, and do not verify the length of data items. Frequently programmers do not write code to verify the size of data items, either, and when an oversized or undersized data item is copied to the stack, a security breach may occur.
5
⇉ To operation and change operation in differential mathematics (SET) and integral (RESET)⇇
- Besides, if and , which is a common situation as well (for example, in the proof of Cauchy's repeated integration formula), we have:
General form: Differentiation under the integral sign
- Theorem. Let f(x, t) be a function such that both f(x, t) and its partial derivative fx(x, t) are continuous in t and x in some region of the (x, t)-plane, including a(x) ≤ t ≤ b(x), x0 ≤ x ≤ x1. Also suppose that the functions a(x) and b(x) are both continuous and both have continuous derivatives for x0 ≤ x ≤ x1. Then, for x0 ≤ x ≤ x1,
If both upper and lower limits are taken as constants, then the formula takes the shape of an operator equation:
The following three basic theorems on the interchange of limits are essentially equivalent:
- the interchange of a derivative and an integral (differentiation under the integral sign; i.e., Leibniz integral rule);
- the change of order of partial derivatives;
- the change of order of integration (integration under the integral sign; i.e., Fubini's theorem).
Three-dimensional, time-dependent case
Figure 1: A vector field F(r, t) defined throughout space, and a surface Σ bounded by curve ∂Σ moving with velocity v over which the field is integrated.
- F(r, t) is a vector field at the spatial position r at time t,
- Σ is a surface bounded by the closed curve ∂Σ,
- dA is a vector element of the surface Σ,
- ds is a vector element of the curve ∂Σ,
- v is the velocity of movement of the region Σ,
- ∇⋅ is the vector divergence,
- × is the vector cross product,
- The double integrals are surface integrals over the surface Σ, and the line integral is over the bounding curve ∂Σ.
Higher dimensions
The Leibniz integral rule can be extended to multidimensional integrals. In two and three dimensions, this rule is better known from the field of fluid dynamics as the Reynolds transport theorem:The general statement of the Leibniz integral rule requires concepts from differential geometry, specifically differential forms, exterior derivatives, wedge products and interior products. With those tools, the Leibniz integral rule in n dimensions is[2]
However, all of these identities can be derived from a most general statement about Lie derivatives:
- is the region of integration (a submanifold) at a given instant (it does not depend on , since its parametrization as a submanifold defines its position in time),
- is the Lie derivative,
- is the spacetime vector field obtained from adding the unitary vector field in the direction of time to the purely spatial vector field from the previous formulas (i.e, is the spacetime velocity of ),
- is a diffeomorphism from the one-parameter group generated by the flow of , and
- is the image of under such diffeomorphism.
Measure theory statement
Let be an open subset of , and be a measure space. Suppose satisfies the following conditions:- is a Lebesgue-integrable function of for each .
- For almost all , the derivative exists for all .
- There is an integrable function such that for all and almost every .
Proofs
Proof of basic form
LetThe above argument shows that for every sequence {δn} → 0, the sequence is uniformly bounded and converges pointwise to fx. The bounded convergence theorem states that if a sequence of functions on a set of finite measure is uniformly bounded and converges pointwise, then passage of the limit under the integral is valid. In particular, the limit and integral may be exchanged for every sequence {δn} → 0. Therefore, the limit as δ → 0 may be passed through the integral sign.
For a simpler proof using Fubini's theorem, see the references.
Variable limits form
For a continuous real valued function g of one real variable, and real valued differentiable functions and of one real variable,- ,
- . (The lower limit just has to be some number in the domain of )
- .
- .
General form with variable limits
SetAlternative Proof of General Form with Variable Limits, using the Chain Rule
The general form of Leibniz's Integral Rule with variable limits can be derived as a consequence of the basic form of Leibniz's Integral Rule, the Multivariable Chain Rule, and the First Fundamental Theorem of Calculus. Suppose is defined in a rectangle in the plane, for and . Also, assume and the partial derivative are both continuous functions on this rectangle. Suppose are differentiable real valued functions defined on , with values in (i.e. for every ). Now, set- , for and
- , for
Substituting these results into the equation for above gives:
There is a technical point in the proof above which is worth noting: applying the Chain Rule to requires that already be Differentiable. This is where we use our assumptions about . As mentioned above, the partial derivatives of are given by the formulas and . Since is continuous, its integral is also a continuous function, and since is also continuous, these two results show that both the partial derivatives of are continuous. Since continuity of partial derivatives implies differentiability of the function, is indeed differentiable.
Three-dimensional, time-dependent form
At time t the surface Σ in Figure 1 contains a set of points arranged about a centroid . The function can be written asIf v is a constant,
Alternative derivation
Lemma. One has:Similarly if exists and is continuous, then for all ε > 0 there exists Δα such that:
Now, suppose
Examples
General examples
Example 1
Consider the functionIf we differentiate φ(α) with respect to α under the integral sign, we get
Example 2
An example with variable limits:Examples for evaluating a definite integral
Example 3
The principle of differentiating under the integral sign may sometimes be used to evaluate a definite integral. Consider:The definition of φ(α) is now complete:
Example 4
This derivation may be generalized. Note that if we define
Example 5
Here, we consider the integralExample 6
Here, we consider the integralOther problems to solve
There are innumerable other integrals that can be solved using the technique of differentiation under the integral sign. For example, in each of the following cases, the original integral may be replaced by a similar integral having a new parameter α:Applications to series
The measure-theoretic version of differentiation under the integral sign also applies to summation (finite or infinite) by interpreting summation as counting measure. An example of an application is the fact that power series are differentiable in their radius of convergence.In popular culture
Differentiation under the integral sign is mentioned in the late physicist Richard Feynman's best-selling memoir Surely You're Joking, Mr. Feynman! in the chapter "A Different Box of Tools". He describes learning it, while in high school, from an old text, Advanced Calculus (1926), by Frederick S. Woods (who was a professor of mathematics in the Massachusetts Institute of Technology). The technique was not often taught when Feynman later received his formal education in calculus, but using this technique, Feynman was able to solve otherwise difficult integration problems upon his arrival at graduate school at Princeton University:One thing I never did learn was contour integration. I had learned to do integrals by various methods shown in a book that my high school physics teacher Mr. Bader had given me. One day he told me to stay after class. "Feynman," he said, "you talk too much and you make too much noise. I know why. You're bored. So I'm going to give you a book. You go up there in the back, in the corner, and study this book, and when you know everything that's in this book, you can talk again." So every physics class, I paid no attention to what was going on with Pascal's Law, or whatever they were doing. I was up in the back with this book: "Advanced Calculus", by Woods. Bader knew I had studied "Calculus for the Practical Man" a little bit, so he gave me the real works—it was for a junior or senior course in college. It had Fourier series, Bessel functions, determinants, elliptic functions—all kinds of wonderful stuff that I didn't know anything about. That book also showed how to differentiate parameters under the integral sign—it's a certain operation. It turns out that's not taught very much in the universities; they don't emphasize it. But I caught on how to use that method, and I used that one damn tool again and again. So because I was self-taught using that book, I had peculiar methods of doing integrals. The result was, when guys at MIT or Princeton had trouble doing a certain integral, it was because they couldn't do it with the standard methods they had learned in school. If it was contour integration, they would have found it; if it was a simple series expansion, they would have found it. Then I come along and try differentiating under the integral sign, and often it worked. .
6
⇉ SPACE AND TIME on PUSH AND PULL ⇇
Both push and pull drive our galaxy's race through space
Discovery of the 'dipole repeller' confirms that both attraction and repulsion are at play in our extragalactic neighborhood
Although we can't feel it, we're in constant motion: the earth spins on its axis at about 1,600 km/h; it orbits around the sun at about 100,000 km/h; the sun orbits our Milky Way galaxy at about 850,000 km/h; and the Milky Way galaxy and its companion galaxy Andromeda are moving with respect to the expanding universe at roughly 2 million km/h (630 km per second). But what is propelling the Milky Way's race through space?
Until now, scientists assumed that a dense region of the universe is pulling us toward it, in the same way that gravity made Newton's apple fall to earth. The initial "prime suspect" was called the Great Attractor, a region of a half dozen rich clusters of galaxies 150 million lightyears from the Milky Way. Soon after, attention was drawn to an area of more than two dozen rich clusters, called the Shapley Concentration, which sits 600 million lightyears beyond the Great Attractor.By identifying the Dipole Repeller, the researchers were able to reconcile both the direction of the Milky Way's motion and its magnitude. They expect that future ultra-sensitive surveys at optical, near-infrared and radio wavelengths will directly identify the few galaxies expected to lie in this void, and directly confirm the void associated with the Dipole Repeller.
Earth is a time space dimension, so it operates in a way that what fills the space then creates either distance or nearness, a longer time or a shorter time.
Congruence is an amazing word, when you allow the vibration of it to truly sink in. It describes a situation where in the moment (time), you are filling your cells and being with a message that all parts of you is agreeing on (space). If you understand this, then understand that everything that occurs as a response to you, offers you a mirror. For example, you’re a full yes to something, and then you present the idea to someone else and they’re a full no. Do you still remain a full yes? Or do you see it for what it is, you are in congrunece in this moment, and they are not? Do you use this as an opportunity to sharpen your articulation, so they are able to get a clear idea of just how congruent you are? Or do you slink away wounded, contracted and caved in? In response to a no do you strengthen your yes, so that you’re not just in agreement you are also amplified?
If even a small part of you is out of alignment with the rest of you, then over time it will make itself known. That small part will convince you that it’s there to look after your best interest and keep you safe. You can consider it to be your gate keeper of sorts, it wants you to put your money where your mouth is. It will niggle, and niggle, and niggle, and niggle, in a quest for you to make the same decision over, and over, and over, and over. Eventually when enough of you is amplified you’ll have pulled the keeper to your side, the gate opens and this becomes your new way of being. Instantly you feel the change because the world begins to respond very differently to you. That part of your life gets easier, just for a little while.
So pay attention to the areas where you’re broadcasting and amplifying a push pull type of energy. Sending mixed messages into the universe, also making it such that you’re not amplifed enough to become magnetic. You stengthen, then weaken, then weaken, then weaken, then strengthen. The energy is counter productive. Empower your stance, empower your decision and empower your actions.



















![{\displaystyle {\frac {d}{dt}}\iint _{\Sigma (t)}\mathbf {F} (\mathbf {r} ,t)\cdot d\mathbf {A} =\iint _{\Sigma (t)}\left(\mathbf {F} _{t}(\mathbf {r} ,t)+\left[\nabla \cdot \mathbf {F} (\mathbf {r} ,t)\right]\mathbf {v} \right)\cdot d\mathbf {A} -\oint _{\partial \Sigma (t)}\left[\mathbf {v} \times \mathbf {F} (\mathbf {r} ,t)\right]\cdot d\mathbf {s} ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78e1920d1765de7da9577a03567e36b3d9d7409e)
















































![{\displaystyle {\begin{aligned}\Delta \varphi &=\varphi (\alpha +\Delta \alpha )-\varphi (\alpha )\\&=\int _{a+\Delta a}^{b+\Delta b}f(x,\alpha +\Delta \alpha )\,dx-\int _{a}^{b}f(x,\alpha )\,dx\\&=\int _{a+\Delta a}^{a}f(x,\alpha +\Delta \alpha )\,dx+\int _{a}^{b}f(x,\alpha +\Delta \alpha )\,dx+\int _{b}^{b+\Delta b}f(x,\alpha +\Delta \alpha )\,dx-\int _{a}^{b}f(x,\alpha )\,dx\\&=-\int _{a}^{a+\Delta a}f(x,\alpha +\Delta \alpha )\,dx+\int _{a}^{b}[f(x,\alpha +\Delta \alpha )-f(x,\alpha )]\,dx+\int _{b}^{b+\Delta b}f(x,\alpha +\Delta \alpha )\,dx.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e844395c738c2319ff0faec99332420bafce02d)

![{\displaystyle \Delta \varphi =-\Delta af(\xi _{1},\alpha +\Delta \alpha )+\int _{a}^{b}[f(x,\alpha +\Delta \alpha )-f(x,\alpha )]\,dx+\Delta bf(\xi _{2},\alpha +\Delta \alpha ).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3e36563c2c4e6f252b197fdf0c03db2e68b869c)




![{\displaystyle x\in [x_{1},x_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/28267d22f13c327a49b44a9cb3f3e4cd38b39d13)
![{\displaystyle t\in [t_{1},t_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3e34a2927bca2a13a30ae0e6fc3a757366e0ba6)


![{\displaystyle [x_{1},x_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91bdff343d848c2b70c68b5c04a2479b14a9fef0)
![{\displaystyle [t_{1},t_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e35e13fa8221f864808f15cafa3d1467b5d78ce)
![{\displaystyle x\in [x_{1},x_{2}],a(x),b(x)\in [t_{1},t_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c47e98fcb040ce05754e1e93c3342f483b47d5e)

![{\displaystyle y\in [t_{1},t_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b3dbc62b50259c75e078c02fbf9d36176b69611)























![{\displaystyle {\begin{aligned}{\frac {\partial }{\partial b}}\left(\int _{a}^{b}f(x)\,dx\right)&=\lim _{\Delta b\to 0}{\frac {1}{\Delta b}}\left[\int _{a}^{b+\Delta b}f(x)\,dx-\int _{a}^{b}f(x)\,dx\right]\\&=\lim _{\Delta b\to 0}{\frac {1}{\Delta b}}\int _{b}^{b+\Delta b}f(x)\,dx\\&=\lim _{\Delta b\to 0}{\frac {1}{\Delta b}}\left[f(b)\Delta b+O\left(\Delta b^{2}\right)\right]\\&=f(b),\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8cc613cf0ffb14b36116c6b713274f4606723c8)
![{\displaystyle {\begin{aligned}{\frac {\partial }{\partial a}}\left(\int _{a}^{b}f(x)\,dx\right)&=\lim _{\Delta a\to 0}{\frac {1}{\Delta a}}\left[\int _{a+\Delta a}^{b}f(x)\,dx-\int _{a}^{b}f(x)\,dx\right]\\&=\lim _{\Delta a\to 0}{\frac {1}{\Delta a}}\int _{a+\Delta a}^{a}f(x)\,dx\\&=\lim _{\Delta a\to 0}{\frac {1}{\Delta a}}\left[-f(a)\Delta a+O\left(\Delta a^{2}\right)\right]\\&=-f(a).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec95fceffc789ee8cb714bee89fb8232cdccd47b)





![{\displaystyle \forall x\in [a,b],\quad \left|{\frac {f(x,\alpha +\Delta \alpha )-f(x,\alpha )}{\Delta \alpha }}-{\frac {\partial f}{\partial \alpha }}\right|<\varepsilon .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3c46cc29cd17e5bba84da7e4b546591b803820c)





![{\displaystyle \Delta \varphi =-\Delta a\,f(\xi _{1},\alpha +\Delta \alpha )+\int _{a}^{b}[f(x,\alpha +\Delta \alpha )-f(x,\alpha )]\,dx+\Delta b\,f(\xi _{2},\alpha +\Delta \alpha ).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/81c03a4ea6d77c7f3f621471c4d7b1522e9da0f3)





































Tidak ada komentar:
Posting Komentar