GO LOOK IMPORTANTBOOK

Gravitational waves permanently change spacetime, say astroboffins ...

MATCOPROC ( Math_Matic of Command Procedure )

=======================================

Number , Variable , Function to record the reality of a timeline

Number is a one of the basic concepts of mathematics . it is originated in ancient times and has undergone expansion and generalisation over the centuries .

Whole number and fractions , both positive and negative , together with the number zero are called rational numbers . every rational number may be represented in the form of ratio a/c , of two integers a and c.

Rational numbers may be represented in the form of periodic terminating or non terminating fractions . Numbers represented by nonterminating , but non periodic , decimal fractions are called irrational numbers .

Real numbers may be depicted as points on a number scale . a number scale is an infinite straight line on which are chosen :

1) a certain point O call the origin .

2) a positive direction indicated by an arrow and

3) a suitable unit length .

we shall usually make the number scale horizontal and take the positive direction to be from left to right.

The Absolute Value of a real number for mission to development of tolerance procedures for electronic components, fatigue of electronic circuit systems, limited control systems and materials science .

=========================================================================

The precise term in "non-negative." Absolute value is a magnitude and is either positive or zero. Zero is neither positive nor negative. But the absolute value of any non-zero number can be thought of as it's distance from zero and it will always be positive.

Absolute Value Inequalities

Here are the steps to follow when solving absolute value inequalities:

Isolate the absolute value expression on the left side of the inequality.
If the number on the other side of the inequality sign is negative, your equation either has no solution or all real numbers as solutions. Use the sign of each side of your inequality to decide which of these cases holds. If the number on the other side of the inequality sign is positive, proceed to step 3.
Remove the absolute value bars by setting up a compound inequality. The type of inequality sign in the problem will tell us how to set up the compound inequality.

If your problem has a greater than sign (your problem now says that an absolute value is greater than a number), then set up an "or" compound inequality that looks like this:

(quantity inside absolute value) < -(number on other side)
OR
(quantity inside absolute value) > (number on other side)

The same setup is used for a ³ sign.

If your absolute value is less than a number, then set up a three-part compound inequality that looks like this:

-(number on other side) < (quantity inside absolute value) < (number on other side)

The same setup is used for a £ sign

Solve the inequalities.

This process can be a little confusing at first, so be patient while learning how to do these problems. Let’s look at some examples.

Example 1: |x + 4| - 6 < 9

Step 1: Isolate the absolute value	\|x + 4\| - 6 < 9 \|x + 4\| < 15
Step 2: Is the number on the other side negative?	No, it’s a positive number, 15. We’ll move on to step 3.
Step 3: Set up a compound inequality	The inequality sign in our problem is a less than sign, so we will set up a 3-part inequality: -15 < x + 4 < 15
Step 4: Solve the compound inequality	-19 < x < 11

Example 2: |2x – 1| - 7 ³ -3

Step 1: Isolate the absolute value	\|2x – 1\| - 7 ³ -3 \|2x – 1\| ³ 4
Step 2: Is the number on the other side a negative number?	No, it’s a positive number, 4. We’ll move on to step 3.
Step 3: Set up a compound inequality	The inequality sign in our problem is a greater than or equal to sign, so we will set up a compound inequality with the word "or": 2x – 1 £ -4 or 2x – 1 ³ 4
Step 4: Solve the inequalities	2x – 1 £ -4 or 2x – 1 ³ 4 2x £ -3 or 2x ³ 5 x £ -3/2 or x ³ 5/2

Example 3: |5x + 6| + 4 < 1

Step 1: Isolate the absolute value

|5x + 6| + 4 < 1

|5x + 6| < -3

Step 2: Is the number on the other side a negative number?

Yes, it’s a negative number, -3.

We’ll look at the signs of each side of the inequality to determine the solution to the problem:

|5x + 6| < -3

positive < negative

This statement is never true, so there is no solution to this problem.

Example 4: |3x – 4| + 9 > 5

Step 1: Isolate the absolute value

|3x – 4| + 9 > 5

|3x – 4| > -4

Step 2: Is the number on the other side a negative number?

Yes, it’s a negative number, -4.

We’ll look at the signs of each side of the inequality to determine the solution to the problem:

|3x – 4| > -4

positive > negative

This statement is always true, so the solution to the problem is All Real Numbers

How do you solve absolute value equations and inequalities?

Key Takeaways

To solve an absolute value equation, such as |X|=p, replace it with the two equations X=−p and X=p. ...
To solve an absolute value inequality involving “less than,” such as |X|≤p, replace it with the compound inequality −p≤X≤p and then solve as usual.

This pattern for "greater than" absolute-value inequalities always holds: Given the inequality | x | > a, the solution always starts by splitting the inequality into two pieces: x < –a or x > a. And, by the way, the correct conjunction is "or", not "and". Absolute Value Inequalities are usually proved by the absolute value of a certain value is greater than or equal to it. The square of the value is equal to the square of its absolute value.

The symbol for absolute value is a bar ∣ on each side of the number. ∣ − 6 ∣ |-6| ∣−6∣vertical bar, minus, 6, vertical bar.

absolute value :

Useful Properties

|a| ≥ 0 always! That makes sense ... |a| can never be less than zero.
|a| = √(a²) Squaring a makes it positive or zero (for a as a Real Number). ...
|a × b| = |a| × |b| Means these are the same: ...
|u| = a is the same as u = ±a and vice versa. Which is often the key to solving most absolute value questions.

The absolute value of −9 is 9.
The absolute value of 3 is 3.
The absolute value of 0 is 0.
The absolute value of −156 is 156.

Absolute Value Functions
==========================

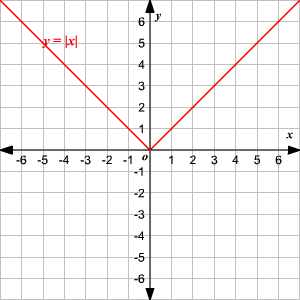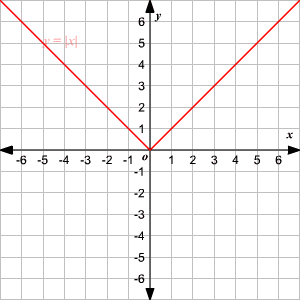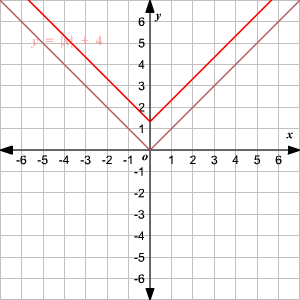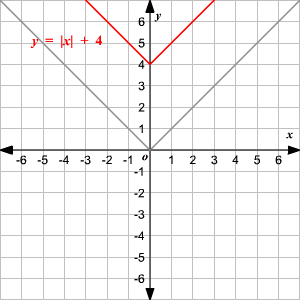
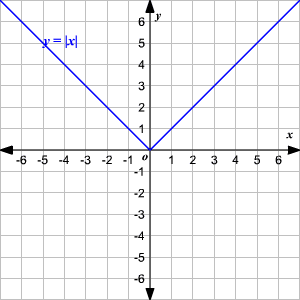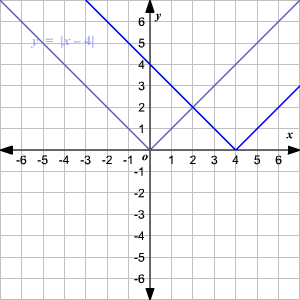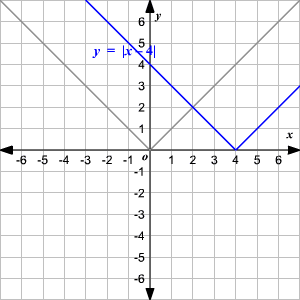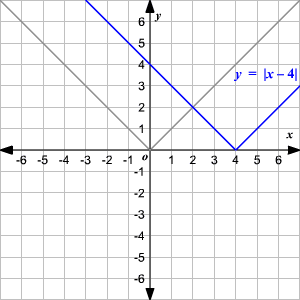
An absolute value function is a function that contains an algebraic expression within absolute value symbols. Recall that the absolute value of a number is its distance from $0$
on the number line.

The absolute value parent function, written as $f (x) = | x |$
, is defined as

$f (x) = {\begin{cases} x if x > 0 \\ 0 if x = 0 \\ - x if x < 0 \end{cases}$

To graph an absolute value function, choose several values of $x$
and find some ordered pairs.

$x$

$y = | x |$

−2 2

−1 1

0 0

1 1

2 2

Plot the points on a coordinate plane and connect them.

Observe that the graph is V-shaped.

( $1$ ) The vertex of the graph is $(0, 0)$
.

( $2$ ) The axis of symmetry ( $x = 0$ or $y$
-axis) is the line that divides the graph into two congruent halves.

( $3$ ) The domain is the set of all real numbers.

( $4$ ) The range is the set of all real numbers greater than or equal to $0$ . That is, $y \geq 0$
.

( $5$ ) The $x$ -intercept and the $y$ -intercept are both $0$
.

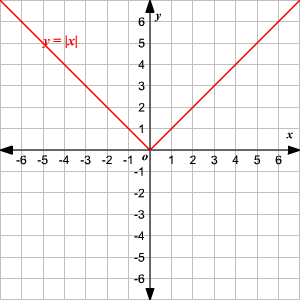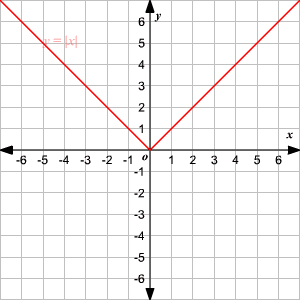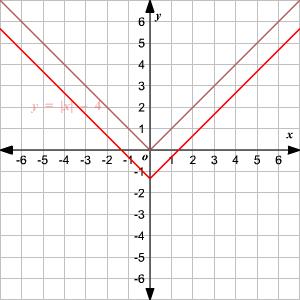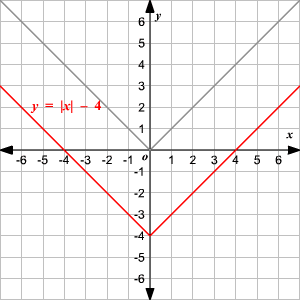
Vertical Shift

To translate the absolute value function $f (x) = | x |$
vertically, you can use the function

$g (x) = f (x) + k$
.

When $k > 0$ , the graph of $g (x)$ translated $k$ units up.

When $k < 0$ , the graph of $g (x)$ translated $k$ units down.

Horizontal Shift

To translate the absolute value function $f (x) = | x |$
horizontally, you can use the function
$g (x) = f (x - h)$ .
When $h > 0$ , the graph of $f (x)$ is translated $h$ units to the right to get $g (x)$ .

When $h < 0$ , the graph of $f (x)$ is translated $h$ units to the left to get $g (x)$ .

Stretch and Compression

The stretching or compressing of the absolute value function $y = | x |$
is defined by the function $y = a | x |$ where $a$ is a constant. The graph opens up if $a > 0$ and opens down when $a < 0$
.

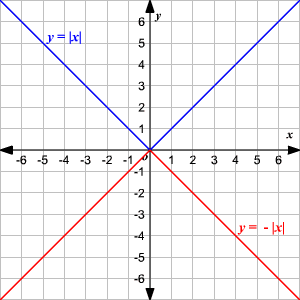
For absolute value equations multiplied by a constant $(for example, y = a | x |)$ ,
if $0 < a < 1$ , then the graph is compressed, and if $a > 1$ , it is stretched. Also, if a is negative, then the graph opens downward, instead of upwards as usual. $a > 1$

More generally, the form of the equation for an absolute value function is $y = a | x - h | + k$
. Also:
- The vertex of the graph is $(h, k)$
.

The domain of the graph is set of all real numbers and the range is $y \geq k$

when

a > 0

The domain of the graph is set of all real numbers and the range is $y \leq k$

when

a < 0

The axis of symmetry is $x = h$
.

It opens up if $a > 0$

and opens down if

a < 0

The graph $y = | x |$

can be translated

h

units horizontally and

k

units vertically to get the graph of

y = a | x - h | + k

The graph $y = a | x |$

is wider than the graph of

y = | x |

| a | < 1

and narrower if

| a | > 1

Summary

To solve an equation containing an absolute value, you want to isolate the absolute value expression. Once that is done, you can rewrite the absolute value equation as two equations, where one of the statements equates the value within the absolute value to the positive quantity on the other side of the equation and one that equates the value with the absolute value to the negative (or opposite) value.

Inequalities can also contain absolute values. Absolute inequalities also can be solved by rewriting them using compound inequalities.

The absolute value of equations and inequalities in the dot matrix system on both analog and digital electronic monitors, namely digital computer monitors that determine the accuracy of the image according to its original form in the time window window in the timeline.

==========================================================================

A point-to-point graph, also called a line graph, is a pictorial rendition of data in which specific values of a function are plotted as dots on a coordinate plane. Adjacent pairs of dots are connected by straight lines.

The horizontal scale across the bottom and the vertical scale along the side tell us how much or how many. The points or dots on the graph represents the x,y coordinates or ordered pairs. The line segments connecting the points give estimated values between th points.

A line plot is a way to display data along a number line. Line plots are also called dot plots.

A line plot is a graph that displays data using a number line. To create a line plot, first create a number line that includes all the values in the data set. Next, place an X (or dot) above each data value on the number line.

Line graphs are used to track changes over short and long periods of time. When smaller changes exist, line graphs are better to use than bar graphs. Line graphs can also be used to compare changes over the same period of time for more than one group.

A Line plot can be defined as a graph that displays data as points or check marks above a number line, showing the frequency of each value.

Clinical assessment of a non-invasive wearable MEMS pressure ...

Highly Sensitive and Wearable Liquid Metal‐Based Pressure Sensor ...

Tolerance design in electronic system performance

========================================

Tolerance design techniques are playing an increasingly important role in maximizing the manufacturing yield of mass-produced electronic circuits. Tolerance Design of Electronic Circuits presents an account of design and analysis methods used to minimize the unwanted effects of component tolerances.

Tolerance Analysis and Design to be calculate :

• the Statistical Exploration Approach to tolerance design

• the Monte Carlo statistical method

• the application of tolerance design

Tolerance Analysis an design using for Electronic Circuit Designers, Computer Aided Design Specialists, Electronic Engineering in Advanced Electronic Circuit Design.

MATCOPROC study compare :

The Problem electronic circuit performance
Concepts and Representations
Tolerance Analysis
The Monte Carlo Method
Tolerance Sensitivity
An Overview of Tolerance Design
Simple Methods Using Performance Calculations
Methods Using Yield Gradients
The Use of Sensitivity Analysis

Control Systems/Poles and Zeros

======================================================================

poles in electronics :

Poles: A switch pole refers to the number of separate circuits that the switch controls. A single-pole switch controls just one circuit. A double-pole switch controls two separate circuits. ... Thus, a double-pole switch has three terminals. One of the terminals is called the common terminal.

Poles and Zeros of a transfer function are the frequencies for which the value of the denominator and numerator of transfer function becomes zero respectively. The values of the poles and the zeros of a system determine whether the system is stable, and how well the system performs. Control systems, in the most simple sense, can be designed simply by assigning specific values to the poles and zeros of the system.

Physically realizable control systems must have a number of poles greater than the number of zeros. Systems that satisfy this relationship are called Proper.

Effects of Poles and Zeros

As s approaches a zero, the numerator of the transfer function (and therefore the transfer function itself) approaches the value 0. When s approaches a pole, the denominator of the transfer function approaches zero, and the value of the transfer function approaches infinity. An output value of infinity should raise an alarm bell for people who are familiar with BIBO stability. We will discuss this later.

As we have seen above, the locations of the poles, and the values of the real and imaginary parts of the pole determine the response of the system. Real parts correspond to exponentials, and imaginary parts correspond to sinusoidal values. Addition of poles to the transfer function has the effect of pulling the root locus to the right, making the system less stable. Addition of zeros to the transfer function has the effect of pulling the root locus to the left, making the system more stable.

Damping Ratio

The damping ratio of a second-order system, denoted with the Greek letter zeta (ζ), is a real number that defines the damping properties of the system. More damping has the effect of less percent overshoot, and slower settling time. Damping is the inherent ability of the system to oppose the oscillatory nature of the system's transient response. Larger values of damping coefficient or damping factor produces transient responses with lesser oscillatory nature.

Natural Frequency

The natural frequency is occasionally written with a subscript:

\omega \to \omega _{n}

We will omit the subscript when it is clear that we are talking about the natural frequency, but we will include the subscript when we are using other values for the variable ω. Also, $\omega ~=~\omega _{n}$ when $\zeta ~=0$ .

Control Systems is an inter-disciplinary engineering text that analyzes the effects and interactions of mathematical systems.

Poles and Zeros in the Z-Plane

===================================================================

Usa Papel de parede Papel de paredes Usa Papel de parede Usaa Bank ... Moving with the times - Business Traveller Africa US Space Force Art | Spaceship US Flag Astronaut Light Art Print ...