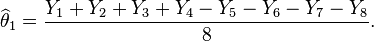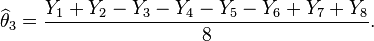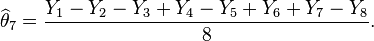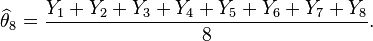The theoretical basis of blocking is the following mathematical result. Given random variables, X and Y
\operatorname{Var}(X-Y)= \operatorname{Var}(X) + \operatorname{Var}(Y) - 2\operatorname{Cov}(X,Y).
The difference between the treatment and the control can thus be given minimum variance (i.e. maximum precision) by maximising the covariance (or the correlation) between X and Y.
This reduces sources of variability and thus leads to greater precision.
Use
Reducing known variability is exactly what blocking does. Its principle lies in the fact that a variability that cannot be overcome (e.g. needing two batches of raw material to produce 1 container of a chemical) is confounded or aliased with a(n) (higher/highest order) interaction to eliminate its influence on the end product. High order interactions are usually of the least importance (think of the fact that temperature of a reactor or the batch of raw materials is more important than the combination of the two - this is especially true when more (3, 4, ...) factors are present) thus it is preferable to confound this variability with the higher interaction.
Suppose a process is invented that intends to make the soles of shoes last longer, and a plan is formed to conduct a field trial. Given a group of n volunteers, one possible design would be to give n/2 of them shoes with the new soles and n/2 of them shoes with the ordinary soles, randomizing the assignment of the two kinds of soles. This type of experiment is a completely randomized design. Both groups are then asked to use their shoes for a period of time, and then measure the degree of wear of the soles. This is a workable experimental design, but purely from the point of view of statistical accuracy (ignoring any other factors), a better design would be to give each person one regular sole and one new sole, randomly assigning the two types to the left and right shoe of each volunteer. Such a design is called a randomized complete block design. This design will be more sensitive than the first, because each person is acting as their own control and thus the control group is more closely matched to the treatment group.
Theoretical basis
blocking instance variable
The design of experiments (DOE, DOX, or experimental design) is the design of any task that aims to describe or explain the variation of information under conditions that are hypothesized to reflect the variation. The term is generally associated with true experiments in which the design introduces conditions that directly affect the variation, but may also refer to the design of quasi-experiments, in which natural conditions that influence the variation are selected for observation.
In its simplest form, an experiment aims at predicting the outcome by introducing a change of the preconditions, which is reflected in a variable called the predictor. The change in the predictor is generally hypothesized to result in a change in the second variable, hence called the outcome variable. Experimental design involves not only the selection of suitable predictors and outcomes, but planning the delivery of the experiment under statistically optimal conditions given the constraints of available resources.
Main concerns in experimental design include the establishment of validity, reliability, and replicability. For example, these concerns can be partially addressed by carefully choosing the predictor, reducing the risk of measurement error, and ensuring that the documentation of the method is sufficiently detailed. Related concerns include achieving appropriate levels of statistical power and sensitivity.
Correctly designed experiments advance knowledge in the natural and social sciences and engineering. Other applications include marketing and policy making.
Lind limited his subjects to men who "were as similar as I could have them", that is he provided strict entry requirements to reduce extraneous variation. He divided them into six pairs, giving each pair different supplements to their basic diet for two weeks. The treatments were all remedies that had been proposed:
- A quart of cider every day.
- Twenty five gutts (drops) of vitriol (sulphuric acid) three times a day upon an empty stomach.
- One half-pint of seawater every day.
- A mixture of garlic, mustard, and horseradish in a lump the size of a nutmeg.
- Two spoonfuls of vinegar three times a day.
- Two oranges and one lemon every day.
A methodology for designing experiments was proposed by Ronald Fisher, in his innovative books: The Arrangement of Field Experiments (1926) and The Design of Experiments (1935). Much of his pioneering work dealt with agricultural applications of statistical methods. As a mundane example, he described how to test the lady tasting tea hypothesis, that a certain lady could distinguish by flavour alone whether the milk or the tea was first placed in the cup. These methods have been broadly adapted in the physical and social sciences, are still used in agricultural engineering and differ from the design and analysis of computer experiments.
- Comparison
- In some fields of study it is not possible to have independent measurements to a traceable metrology standard. Comparisons between treatments are much more valuable and are usually preferable, and often compared against a scientific control or traditional treatment that acts as baseline.
- Randomization
- Random assignment is the process of assigning individuals at random to groups or to different groups in an experiment, so that each individual of the population has the same chance of becoming a participant in the study. The random assignment of individuals to groups (or conditions within a group) distinguishes a rigorous, "true" experiment from an observational study or "quasi-experiment".[12] There is an extensive body of mathematical theory that explores the consequences of making the allocation of units to treatments by means of some random mechanism such as tables of random numbers, or the use of randomization devices such as playing cards or dice. Assigning units to treatments at random tends to mitigate confounding, which makes effects due to factors other than the treatment to appear to result from the treatment. The risks associated with random allocation (such as having a serious imbalance in a key characteristic between a treatment group and a control group) are calculable and hence can be managed down to an acceptable level by using enough experimental units. However, if the population is divided into several subpopulations that somehow differ, and the research requires each subpopulation to be equal in size, stratified sampling can be used. In that way, the units in each subpopulation are randomized, but not the whole sample. The results of an experiment can be generalized reliably from the experimental units to a larger statistical population of units only if the experimental units are a random sample from the larger population; the probable error of such an extrapolation depends on the sample size, among other things.
- Statistical replication
- Measurements are usually subject to variation and measurement uncertainty; thus they are repeated and full experiments are replicated to help identify the sources of variation, to better estimate the true effects of treatments, to further strengthen the experiment's reliability and validity, and to add to the existing knowledge of the topic.[13] However, certain conditions must be met before the replication of the experiment is commenced: the original research question has been published in a peer-reviewed journal or widely cited, the researcher is independent of the original experiment, the researcher must first try to replicate the original findings using the original data, and the write-up should state that the study conducted is a replication study that tried to follow the original study as strictly as possible.[14]
- Blocking
- Blocking is the arrangement of experimental units into groups (blocks/lots) consisting of units that are similar to one another. Blocking reduces known but irrelevant sources of variation between units and thus allows greater precision in the estimation of the source of variation under study.
Example of orthogonal factorial design
- Orthogonality concerns the forms of comparison (contrasts) that can be legitimately and efficiently carried out. Contrasts can be represented by vectors and sets of orthogonal contrasts are uncorrelated and independently distributed if the data are normal. Because of this independence, each orthogonal treatment provides different information to the others. If there are T treatments and T – 1 orthogonal contrasts, all the information that can be captured from the experiment is obtainable from the set of contrasts.
- Factorial experiments
- Use of factorial experiments instead of the one-factor-at-a-time method. These are efficient at evaluating the effects and possible interactions of several factors (independent variables). Analysis of experiment design is built on the foundation of the analysis of variance, a collection of models that partition the observed variance into components, according to what factors the experiment must estimate or test.
- This example is attributed to Harold Hotelling.It conveys some of the flavor of those aspects of the subject that involve combinatorial designs.
Weights of eight objects are measured using a pan balance and set of standard weights. Each weighing measures the weight difference between objects in the left pan vs. any objects in the right pan by adding calibrated weights to the lighter pan until the balance is in equilibrium. Each measurement has a random error. The average error is zero; the standard deviations of the probability distribution of the errors is the same number σ on different weighings; and errors on different weighings are independent. Denote the true weights by
- Weigh each object in one pan, with the other pan empty. Let Xi be the measured weight of the object, for i = 1, ..., 8.
- Do the eight weighings according to the following schedule and let Yi be the measured difference for i = 1, ..., 8:
- Then the estimated value of the weight θ1 is
- Similar estimates can be found for the weights of the other items. For example
The variance of the estimate X1 of θ1 is σ2 if we use the first experiment. But if we use the second experiment, the variance of the estimate given above is σ2/8. Thus the second experiment gives us 8 times as much precision for the estimate of a single item, and estimates all items simultaneously, with the same precision. What the second experiment achieves with eight would require 64 weighings if the items are weighed separately. However, note that the estimates for the items obtained in the second experiment have errors that correlate with each other.
Many problems of the design of experiments involve combinatorial designs, as in this example and others.
Avoiding false positives
False positive conclusions, often resulting from the pressure to publish or the author's own confirmation bias, are an inherent hazard in many fields. A good way to prevent biases potentially leading to false positives in the data collection phase is to use a double-blind design. When a double-blind design is used, participants are randomly assigned to experimental groups but the researcher is unaware of what participants belong to which group. Therefore, the researcher can not affect the participants' response to the intervention. Experimental designs with undisclosed degrees of freedom are a problem. This can lead to conscious or unconscious "p-hacking": trying multiple things until you get the desired result. It typically involves the manipulation - perhaps unconsciously - of the process of statistical analysis and the degrees of freedom until they return a figure below the p<.05 level of statistical significance. So the design of the experiment should include a clear statement proposing the analyses to be undertaken. P-hacking can be prevented by preregistering researches, in which researchers have to send their data analysis plan to the journal they wish to publish their paper in before they even start their data collection, so no data mining is possible . Another way to prevent this is taking the double-blind design to the data-analysis phase, where the data are sent to a data-analyst unrelated to the research who scrambles up the data so there is no way to know which participants belong to before they are potentially taken away as outliers.Clear and complete documentation of the experimental methodology is also important in order to support replication of results.
Discussion topics when setting up an experimental design
An experimental design or randomized clinical trial requires careful consideration of several factors before actually doing the experiment. An experimental design is the laying out of a detailed experimental plan in advance of doing the experiment. Some of the following topics have already been discussed in the principles of experimental design section:- How many factors does the design have? and are the levels of these factors fixed or random?
- Are control conditions needed, and what should they be?
- Manipulation checks; did the manipulation really work?
- What are the background variables?
- What is the sample size. How many units must be collected for the experiment to be generalisable and have enough power?
- What is the relevance of interactions between factors?
- What is the influence of delayed effects of substantive factors on outcomes?
- How do response shifts affect self-report measures?
- How feasible is repeated administration of the same measurement instruments to the same units at different occasions, with a post-test and follow-up tests?
- What about using a proxy pretest?
- Are there lurking variables?
- Should the client/patient, researcher or even the analyst of the data be blind to conditions?
- What is the feasibility of subsequent application of different conditions to the same units?
- How many of each control and noise factors should be taken into account?
Causal attributions
In the pure experimental design, the independent (predictor) variable is manipulated by the researcher - that is - every participant of the research is chosen randomly from the population, and each participant chosen is assigned randomly to conditions of the independent variable. Only when this is done is it possible to certify with high probability that the reason for the differences in the outcome variables are caused by the different conditions. Therefore, researchers should choose the experimental design over other design types whenever possible. However, the nature of the independent variable does not always allow for manipulation. In those cases, researchers must be aware of not certifying about causal attribution when their design doesn't allow for it. For example, in observational designs, participants are not assigned randomly to conditions, and so if there are differences found in outcome variables between conditions, it is likely that there is something other than the differences between the conditions that causes the differences in outcomes, that is - a third variable. The same goes for studies with correlational design. (Adér & Mellenbergh, 2008).Statistical control
It is best that a process be in reasonable statistical control prior to conducting designed experiments. When this is not possible, proper blocking, replication, and randomization allow for the careful conduct of designed experiments. To control for nuisance variables, researchers institute control checks as additional measures. Investigators should ensure that uncontrolled influences (e.g., source credibility perception) do not skew the findings of the study. A manipulation check is one example of a control check. Manipulation checks allow investigators to isolate the chief variables to strengthen support that these variables are operating as planned.One of the most important requirements of experimental research designs is the necessity of eliminating the effects of spurious, intervening, and antecedent variables. In the most basic model, cause (X) leads to effect (Y). But there could be a third variable (Z) that influences (Y), and X might not be the true cause at all. Z is said to be a spurious variable and must be controlled for. The same is true for intervening variables (a variable in between the supposed cause (X) and the effect (Y)), and anteceding variables (a variable prior to the supposed cause (X) that is the true cause). When a third variable is involved and has not been controlled for, the relation is said to be a zero order[disambiguation needed] relationship. In most practical applications of experimental research designs there are several causes (X1, X2, X3). In most designs, only one of these causes is manipulated at a time.
Experimental designs after Fisher
Some efficient designs for estimating several main effects were found independently and in near succession by Raj Chandra Bose and K. Kishen in 1940 at the Indian Statistical Institute, but remained little known until the Plackett-Burman designs were published in Biometrika in 1946. About the same time, C. R. Rao introduced the concepts of orthogonal arrays as experimental designs. This concept played a central role in the development of Taguchi methods by Genichi Taguchi, which took place during his visit to Indian Statistical Institute in early 1950s. His methods were successfully applied and adopted by Japanese and Indian industries and subsequently were also embraced by US industry albeit with some reservations.In 1950, Gertrude Mary Cox and William Gemmell Cochran published the book Experimental Designs, which became the major reference work on the design of experiments for statisticians for years afterwards.
Developments of the theory of linear models have encompassed and surpassed the cases that concerned early writers. Today, the theory rests on advanced topics in linear algebra, algebra and combinatorics.
As with other branches of statistics, experimental design is pursued using both frequentist and Bayesian approaches: In evaluating statistical procedures like experimental designs, frequentist statistics studies the sampling distribution while Bayesian statistics updates a probability distribution on the parameter space.
Human participant experimental design constraints
Plackett–Burman designs are experimental designs presented in 1946 by Robin L. Plackett and J. P. Burman while working in the British Ministry of Supply. Their goal was to find experimental designs for investigating the dependence of some measured quantity on a number of independent variables (factors), each taking L levels, in such a way as to minimize the variance of the estimates of these dependencies using a limited number of experiments. Interactions between the factors were considered negligible. The solution to this problem is to find an experimental design where each combination of levels for any pair of factors appears the same number of times, throughout all the experimental runs (refer table). A complete factorial design would satisfy this criterion, but the idea was to find smaller designs.
| Run | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | X11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | + | + | + | + | + | + | + | + | + | + | + |
| 2 | − | + | − | + | + | + | − | − | − | + | − |
| 3 | − | − | + | − | + | + | + | − | − | − | + |
| 4 | + | − | − | + | − | + | + | + | − | − | − |
| 5 | − | + | − | − | + | − | + | + | + | − | − |
| 6 | − | − | + | − | − | + | − | + | + | + | − |
| 7 | − | − | − | + | − | − | + | − | + | + | + |
| 8 | + | − | − | − | + | − | − | + | − | + | + |
| 9 | + | + | − | − | − | + | − | − | + | − | + |
| 10 | + | + | + | − | − | − | + | − | − | + | − |
| 11 | − | + | + | + | − | − | − | + | − | − | + |
| 12 | + | − | + | + | + | − | − | − | + | − | − |
For the case of more than two levels, Plackett and Burman rediscovered designs that had previously been given by Raj Chandra Bose and K. Kishen at the Indian Statistical Institute.[4] Plackett and Burman give specifics for designs having a number of experiments equal to the number of levels L to some integer power, for L = 3, 4, 5, or 7.
When interactions between factors are not negligible, they are often confounded in Plackett–Burman designs with the main effects, meaning that the designs do not permit one to distinguish between certain main effects and certain interactions. This is called aliasing or confounding.
Extended uses
In 1993, Dennis Lin described a construction method via half-fractions of Plackett-Burman designs, using one column to take half of the rest of the columns. The resulting matrix, minus that column, is a "supersaturated design" for finding significant first order effects, under the assumption that few exist.Box-Behnken designs can be made smaller, or very large ones constructed, by replacing the fractional factorials and incomplete blocks traditionally used for plan and seed matrices, respectively, with Plackett-Burmans. For example, a quadratic design for 30 variables requires a 30 column PB plan matrix of zeroes and ones, replacing the ones in each line using PB seed matrices of -1s and +1s (for 15 or 16 variables) wherever a one appears in the plan matrix, creating a 557 runs design with values, -1, 0, +1, to estimate the 496 parameters of a full quadratic model.
By equivocating certain columns with parameters to be estimated, Plackett-Burmans can also be used to construct mixed categorical and numerical designs, with interactions or high order effects, requiring no more than 4 runs more than the number of model parameters to be estimated. Sort on columns assigned to categorical variable "A", defined as A = 1+int(a*i /(max(i)+.00001)) where i is row number and a is A's number of values. Next sort on columns assigned to any other categorical variables and repeat as needed. Such designs, if large, may otherwise be incomputable by standard search techniques like D-Optimality. For example, 13 variables averaging 3 values each could have well over a million combinations to search. To estimate roughly 100 parameters for a nonlinear model in 13 variables must formally exclude from consideration or compute |X'X| for well over 106C102 or roughly 10600 matrices.
Computer simulations are constructed to emulate a physical system. Because these are meant to replicate some aspect of a system in detail, they often do not yield an analytic solution. Therefore, methods such as discrete event simulation or finite element solvers are used. A computer model is used to make inferences about the system it replicates. For example, climate models are often used because experimentation on an earth sized object is impossible.
Objectives
Computer experiments have been employed with many purposes in mind. Some of those include:- Uncertainty quantification: Characterize the uncertainty present in a computer simulation arising from unknowns during the computer simulation's construction.
- Inverse problems: Discover the underlying properties of the system from the physical data.
- Bias correction: Use physical data to correct for bias in the simulation.
- Data assimilation: Combine multiple simulations and physical data sources into a complete predictive model.
- Systems design: Find inputs that result in optimal system performance measures.
Computer simulation modeling
The basic idea of this framework is to model the computer simulation as an unknown function of a set of inputs. The computer simulation is implemented as a piece of computer code that can be evaluated to produce a collection of outputs. Examples of inputs to these simulations are coefficients in the underlying model, initial conditions and forcing functions. It is natural to see the simulation as a deterministic function that maps these inputs into a collection of outputs. On the basis of seeing our simulator this way, it is common to refer to the collection of inputs as
, the computer simulation itself as 
, and the resulting output as 
. Both and
are vector quantities, and they can be very large collections of
values, often indexed by space, or by time, or by both space and time.Although
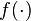is known in principle, in practice this is not the case. Many
simulators comprise tens of thousands of lines of high-level computer
code, which is not accessible to intuition. For some simulations, such
as climate models, evaluation of the output for a single set of inputs
can require millions of computer hours .Gaussian process prior
The typical model for a computer code output is a Gaussian process. For notational simplicity, assume is a scalar. Owing to the Bayesian framework, we fix our belief that the function follows a Gaussian process,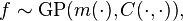 
where 
is the mean function and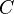 
is the covariance function. Popular mean functions are low order polynomials and a popular covariance function is Matern covariance, which includes both the exponential (
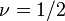) and Gaussian covariances (as 
).Design of computer experiments
Popular strategies for design include latin hypercube sampling and low discrepancy sequences.
Problems with massive sample sizes
Unlike physical experiments, it is common for computer experiments to have thousands of different input combinations. Because the standard inference requires matrix inversion of a square matrix of the size of the number of samples (
), the cost grows on the 
.
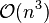Matrix inversion of large, dense matrices can also cause induce
numerical inaccuracies. Currently, this problem is solved by greedy
decision tree techniques, allowing effective computations for unlimited
dimensionality and sample size patent WO2013055257A1, or avoided by using approximation methods, e.g. .The instrument effect is an issue in experimental methodology meaning that any change during the measurement, or, the instrument, may influence the research validity. For example, in a control group design experiment, if the instruments used to measure the performance of the experiment group and the control group are different, a wrong conclusion about the experiment would be reached, the research result would be invalid
Loss functions in statistical theory
Traditionally, statistical methods have relied on mean-unbiased estimators of treatment effects: Under the conditions of the Gauss-Markov theorem, least squares estimators have minimum variance among all mean-unbiased estimators. The emphasis on comparisons of means also draws (limiting) comfort from the law of large numbers, according to which the sample means converge to the true mean. Fisher's textbook on the design of experiments emphasized comparisons of treatment means.However, loss functions were avoided by Ronald A. Fisher.[6]
