ROBOTIC MOBILITY GROUP MASSACHUSET INSTITUTE OF TECHNOLOGY

Terrain Sensing
 
For mobile robots in rough terrain, the ability to safely traverse terrain is highly dependent on mechanical properties of that terrain. For example, a robot may be able to climb up a rocky slope with ease, but slide down a sandy slope the same grade. With mobile robots being employed for planetary exploration and UGVs being developed for missions on Earth, the ability to predict these mechanical terrain properties from a distance is becoming increasingly important.

This project focuses on:

• Classifying natural terrain based on visual features, such as color, visual texture, and range data,
• Learning visual classification on-line, so that a robot can improve its terrain recognition based on its experiences,
• Autonomously identifying mechanically-distinct terrain classes to eliminate the need for human supervision in establishing the list of terrain classes, and
• Estimating the mechanical terrain properties associated with each of the terrain classes.

The goal of this work is to be able to set a robot down in a previously unexplored environment, and after driving around for a short period of time have it be able to look out in the distance and predict mechanical properties of the terrain it sees.

Experiments for this project have been performed using a four-wheeled mobile robot in natural outdoor terrain. The robot appeared briefly in a segment of NOVA scienceNOW.

This work has been funded by NASA/JPL through the Mars Technology Program. 


Mobility Prediction with Environmental Uncertainty
The ability of autonomous unmanned ground vehicles to rapidly and effectively predict terrain negotiability is a critical requirement for their use on challenging terrain. Most of the work done on mobility prediction for such vehicles, however, assumes precise knowledge about the vehicle/terrain properties. In practical conditions though, uncertainties are associated with the estimation of these parameters. This work focuses on developing efficient methods that take into account environmental uncertainty while determining vehicular mobility.

Omnidirectional Mobile Robots in Rough Terrain Mobile robots are finding increasing use in military, disaster recovery, and exploration applications. These applications frequently require operation in rough, unstructured terrain. Currently, most mobile robots designed for these applications are tracked or Ackermann-steered wheeled vehicles. Methods for controlling these types of robots in both smooth and rough terrain have been well studied. While these robots types can perform well in many scenarios, navigation in cluttered, rocky, or obstacle-dense urban environments can be difficult or impossible. This is partly due to the fact that traditional tracked and wheeled robots must reorient to perform some maneuvers, such as lateral displacement. Omnidirectional mobile robots could potentially navigate faster and more reliably through cluttered urban environments and over rough terrain, due to their ability to track near-arbitrary motion profiles. Currently, the drive mechanisms of most omnidirectional mobile robots are designed to perform well in indoor and benign environments. This project focuses on the analysis, design, and control of omnidirectional mobile robots for use in rough terrain. The robots in this study use active split offset caster drive mechanisms that allow high thrust efficiency during omnidirectional motion and low ground pressures over rough terrain. The design guidelines developed in this research are scalable and applicable for a class of omnidirectional mobile robots. MIT is collaborating with the Illinois Institute of Technology in constructing a prototype robot to experimentally validate the effectiveness of the design guidelines and controller. This work has been funded by the U.S. Army Research Office.

 

Trajectory tracking control for front-steered ground vehicles
The ability to follow a desired trajectory is an important part of many autonomous vehicle navigation and hazard avoidance systems. An important requirement for trajectory tracking controllers is appropriate consideration of the vehicle dynamics, especially with regard to wheel slip. When wheel slip is small, the vehicle dynamics are greatly simplified. When wheel slip does occur, however, it can cause a loss of control, such as in the video below showing a lane change maneuver on snow and ice (please skip to 2 minutes 34 seconds if the video does not automatically do so).
One approach to dealing with the loss of control when wheel slip is large is the use of electronic yaw stability control systems. These systems operate by precisely controlling the brakes at individual wheels to minimize sideslip. Such a system is illustrated in the video above at 3 minutes, 55 seconds. These systems have been shown to reduce the risk of crashes, and fatal crashes in particular.
Electronic stability control systems are effective in reducing wheel slip, but they currently do not consider the effect that stability control has on altering the vehicle path and its ability to avoid collisions with hazards. Also, there is evidence that vehicles can be controlled precisely even with large amounts of wheel slip, as evidenced by the Ken Block Gymkhana video shown below (please skip to 2 minutes, 7 seconds if the video does not automatically do so).
Rather than minimizing wheel slip like a conventional stability controller, we suggest compensating for slip while following a desired trajectory, in a similar manner to expert rally drivers. We recently considered a controller that employs feedback control of tire friction forces to control the position of the front center of oscillation along a desired trajectory. This work was inspired by previous work by Ackermann and is similar to concurrent work being done at Stanford's Dynamic Design Lab.
The trajectory tracking controller is based on a planar half-car model that has one steerable wheel at the front and one wheel at the rear. It is also sometimes called a bicycle model, though it is only 2-dimensional and cannot tip over like a 3-dimensional bicycle. An illustration of this model is given below. Friction force F_f and F_r act at the front and rear wheels, and the speed at the center of gravity (c.g.) is V.

The trajectory tracking controller controls the position of a point near the front wheels to follow a desired trajectory. The vehicle behavior is illustrated in the animation below for a sinusoidal trajectory with low acceleration. It can be seen that the front of the vehicle follows the desired trajectory, and the vehicle orientation oscillates a small amount.

Robotics Technology - Mobility

Robotics Technology - Mobility

Industrial robots are rarely mobile. Work is generally brought to the robot. A few industrial robots are mounted on tracks and are mobile within their work station. Service robots are virtually the only kind of robots that travel autonomously. Research on robot mobility is extensive. The goal of the research is usually to have the robot navigate in unstructured environments while encountering unforeseen obstacles. Some projects raise the technical barriers by insisting that the locomotion involve walking, either on two appendages, like humans, or on many, like insects. Most projects, however, use wheels or tractor mechanisms. Many kinds of effectors and actuators can be used to move a robot around. Some categories are:

• legs (for walking/crawling/climbing/jumping/hopping)
• wheels (for rolling)
• arms (for swinging/crawling/climbing)
• flippers (for swimming)

Wheels

Wheels are the locomotion effector of choice. Wheeled robots (as well as almost all wheeled mechanical devices, such as cars) are built to be statically stable. It is important to remember that wheels can be constructed with as much variety and innovative flair as legs: wheels can vary in size and shape, can consist of simple tires, or complex tire patterns, or tracks, or wheels within cylinders within other wheels spinning in different directions to provide different types of locomotion properties. So wheels need not be simple, but typically they are, because even simple wheels are quite efficient.  Having wheels does not imply holonomicity. 2 or 4-wheeled robots are not usually holonomic. A popular and efficient design involves 2 differentially-steerable wheels and a passive caster.  Differential steering means that the two (or more) wheels can be steered separately (individually) and thus differently. If one wheel can turn in one direction and the other in the opposite direction, the robot can spin in place. This is very helpful for following arbitrary trajectories. Tracks are often used (e.g., tanks).

Legs

While most animals use legs to get around, legged locomotion is a very difficult robotic problem, especially when compared to wheeled locomotion.   First, any robot needs to be stable (i.e., not wobble and fall over easily). There are two kinds of stability: static and dynamic. A statically stable robot can stand still without falling over. This is a useful feature, but a difficult one to achieve: it requires that there be enough legs/wheels on the robot to provide sufficient static points of support.  For example, people are not statically stable. In order to stand up, which appears effortless to us, we are actually using active control of our balance, though nerves and muscles and tendons. This balancing is largely unconscious, but must be learned, so that's why it takes babies a while to get it right, and certain injuries can make it difficult or impossible.  With more legs, static stability becomes quite simple. In order to remain stable, the robot's center of gravity (COG) must fall under its polygon of support. This polygon is basically the projection between all of its support points onto the surface. So in a two-legged robot, the polygon is really a line, and the COG cannot be stably aligned with a point on that line to keep the robot upright. However, a three-legged robot, with its legs in a tripod organization, and its body above, produces a stable polygon of support, and is thus statically stable.  But what happens when a statically stable robot lifts a leg and tries to move. Does its COG stay within the polygon of support? It may or may not, depending on the geometry. For certain robot geometries, it is possible (with various numbers of legs) to always stay statically stable while walking. This is very safe, but it is also very slow and energy inefficient.  A basic assumption of the static gait (statically stable gait) is that the weight of a leg is negligible compared to that of the body, so that the total center of gravity (COG) of the robot is not affected by the leg swing. Based on this assumption, the conventional static gait is designed so as to maintain the COG of the robot inside of the support polygon, which is outlined by each support leg's tip position.  The alternative to static stability is dynamic stability which allows a robot (or animal) to be stable while moving. For example, one-legged hopping robots are dynamically stable: they can hop in place or to various destinations, and not fall over. But they cannot stop and stay standing (this is an inverse pendulum balancing problem).  

A statically stable robot can use dynamically-stable walking patterns, to be fast, or it can use statically stable walking. A simple way to think about this is by how many legs are up in the air during the robot's movement (i.e., gait). 6 legs is the most popular number as they allow for a very stable walking gait, the tripod gait . If the same three legs move at a time, this is called the alternating tripod gait. if the legs vary, it is called the ripple gait. A rectangular 6-legged robot can lift three legs at a time to move forward, and still retain static stability. How does it do that? It uses the so-called alternating tripod gait, a biologically common walking pattern for 6 or more legs. In this gait, one middle leg on one side and two non-adjacent legs on the other side of the body lift and move forward at the same time, while the other 3 legs remain on the ground and keep the robot statically stable. Roaches move this way, and can do so very quickly. Insects with more than 6 legs (e.g., centipedes and millipedes), use the ripple gate. However, when they run really fast, they switch gates to actually become airborne (and thus not statically stable) for brief periods of time. 

Statically stable walking is very energy inefficient. As an alternative, dynamic stability enables a robot to stay up while moving. This requires active control (i.e., the inverse pendulum problem). Dynamic stability can allow for greater speed, but requires harder control.  Balance and stability are very difficult problems in control and robotics, so that is why when you look at most existing robots, they will have wheels or plenty of legs (at least 6). Research robotics, of course, is studying single-legged, two legged, and other dynamically-stable robots, for various scientific and applied reasons.  Wheels are more efficient than legs. They also do appear in nature, in certain bacteria, so the common myth that biology cannot make wheels is not well founded. However, evolution favors lateral symmetry and legs are much easier to evolve, as is abundantly obvious. However, if you look at population sizes, insects are most populous animals, and they all have many more than 2 legs.  

The Spider, a Legged Robot

In solving problems, the Spider is aided by the spring quality of its 1 mm steel wire legs. Hold one of its feet in place relative to the body and the mechanism keeps turning, the obstructed motor consuming less than 40 mA while it bends the leg. Let go and the leg springs back into shape. As I write this, the Spider is scrambling up and over my keyboard. Some of its feet get temporarily stuck between keys, springing loose again as others push down. It has no trouble whatsoever with this obstacle, nor with any of the others on my cluttered desk - even though it is still utterly brainless. 

Mobility Limits of the Spider

As the feet rise to a maximum of 2 cm off the floor, a cassette box is about the tallest vertical obstacle that the Spider is able to step onto. Another limitation is slope. When asked to sustain a climb angle of more than about 20 degrees, the Spider rolls over backwards. And even this fairly modest angle (extremely steep for a car, by the way) requires careful gait control, making sure that both rear legs do not lift at the same time. Improvements are certainly possible. Increasing step size would require a longer body (more distance between the legs) and thus a different gear train. A better choice might be more legs, like 10 or 12 on a longer body, but with the same size gear wheels. That would give better traction and climbing ability. And if a third motor is allowed, one might construct a horizontal hinge in the `backbone'. Make a gear shaft the center of a nice, tight hinge joint. Then the drive train will function as before. Using the third motor and a suitable mechanism, the robot could raise its front part to step onto a tall obstacle, somewhat like a caterpillar. But turning on the spot becomes difficult.

Flying and Underwater Robots

Most robots do not fly or swim.  Recently, researchers have been exploring the possibilities and problems involved with flying and swimming robots.              Lookahead Navigation for High-Speed Mobile Robots Recent developments in both defense and commercial sectors have inspired a growing interest in mobile robot navigation technologies. As look-ahead sensing capabilities improve, mobile robots will be able to operate at higher speeds and in more varied environments. This research aims to develop novel planning and control approaches to meet the challenge. Operation at high speeds requires the anticipation of obstacles and terrain changes. In addition, dynamic effects such as friction saturation and loss of ground contact limit the class of feasible vehicle trajectories. A lookahead naviation system must be capable of planning a feasible trajectory through the sensed environment and controlling the vehicle along that trajectory while remaining robust to terrain changes and dynamic disturbances. To achieve this kind of forward-looking, versatile control, we are leveraging the prediction and constraint-handling capabilities of model predictive control. Model Predictive Control (MPC) is a flexible, model-based control approach that seeks to minimize an objective function by optimizing a projected set of control inputs over a progressive and forward-looking time horizon. Its ability to explicitly consider constraints, track references, include environmental disturbances, and incorporate multiple actuation methods make it particularly well-suited for the mobile robot navigation problem.

theory movement arrow

  

Vektor

       Mempelajari Fisika akan lebih mudah dan menarik jika kita memahami bahasa yang digunakan di dalamnya. Apakah bahasa yang dipakai di dalam Fisika? Galileo pernah mengatakan bahwa bahasa tersebut adalah Matematika. Memang, Fisika adalah ilmu yang mempelajari tentang bagaimana alam ini bekerja, namun sayangnya, suka atau tidak, kita tetap melibatkan Matematika. 
       Tanpa bermaksud menurunkan semangat namun justru ingin memberi suatu motivasi, maka bagi pelajar yang benar-benar ingin melihat lebih jauh keindahan dalam Fisika, maka pemahaman Matematika sebagai bahasa yang digunakan dan sebagai dasar tentu adalah hal yang tidak dapat ditawar. Dalam buku ini, kita akan melihat bagian-bagian Matematika yang setidaknya diperlukan untuk mempelajari Fisika di tingkat dasar. Tentunya teknik berhitung dasar dalam matematika harus benar-benar dikuasai dan di dalam buku ini, bagian pertama yang akan dibahas di sini adalah tentang vektor.
        Vektor menjadi salah satu fondasi dalam mempelajari Fisika, hal ini dikarenakan banyak besaran dalam Fisika merupakan vektor. Sebagai contoh adalah perpindahan, kecepatan, percepatan dan gaya. Lebih jauh, operasi hitung pada vektor tidaklah sama seperti kita berhitung dengan besaran skalar.
       Vektor merupakan besaran yang memiliki dua informasi penting, yakni nilai dan arah. Sementara, Skalar merupakan besaran yang hanya memiliki nilai saja. Termasuk dalam skalar adalah: jarak, kelajuan, kuat arus listrik, tekanan, energi dan beberapa besaran lagi yang akan kita pelajari nanti.
       Untuk menggambarkan sebuah vektor, kita dapat menggunakan simbol sebuah anak panah, dimana terdapat bagian runcing yang dinamakan sebagai KEPALA (Head) dan bagian di ujung yang lain yang kita namakan sebagai EKOR (Tail). Kepala anak panah tadi menggambarkan ke arah mana vektor tersebut, sedangkan panjang dari anak panah menyatakan besar/nilai dari vektor tersebut.

Gambar 2.1 Vektor A, B dan C masing-masing digambarkan sebagai anak panah yang menyatakan arah dan besar dari vektor tersebut. Dua buah vektor dikatakan berbeda jika keduanya memiliki besar atau arah (atau keduanya) yang berbeda.

       Untuk menyatakan arah vektor yang mendekati kita dapat digambarkan sebagai sebuah lingkaran kecil dengan titik di tengahnya, sedangkan untuk menyatakan arah vektor yang menjauhi kita dapat digambarkan dengan tanda silang.

Gambar 2.2 Vektor yang arahnya mendekati kita digambarkan sebagai lingkaran dengan titik di tengah sedangkan vector yang arahnya menjauhi kita digambarkan sebagai tanda silang.

       Vektor memiliki operasi hitung yang berbeda dengan operasi hitung yang kita gunakan pada besaran skalar. Pada besaran skalar, misalkan kita menjumlahkan massa 2 benda, yakni 2 kg dan 3 kg, maka kita akan dapati massa total mereka adalah 5 kg. Namun jika kita memiliki 2 vektor gaya, misalkan 2 N dan 3 N, maka jumlah keduanya akan sebesar 5 N apabila kedua vektor tadi memiliki arah yang sama. Namun apabila kedua gaya tadi tidak memiliki arah yang sama, maka hasil penjumlahan kedua gaya tersebut akan menghasilkan hasil yang berbeda, dimana nilainya juga dipengaruhi oleh sudut yang dibentuk antara kedua gaya tersebut. Jadi, jumlah dari 2 buah vektor sangat bergantung dari arah vektor satu terhadap yang lain. 
Misalkan, kita memiliki dua vektor, A dan B seperti pada gambar. Kedua vektor tersebut saling membentuk sudut α. Untuk menjumlahkan kedua vektor ini ada beberapa cara yang dapat kita lakukan:
1. Metode Poligon

2. Metode Jajaran genjang

3. Metode Analitis

Untuk metode ini, kita ambil salah satu vektor, misalnya A. Vektor A ini dapat kita urai menjadi dua buah komponen, yaitu A_x yang sejajar dengan vektor B dan A_y yang tegak lurus dengan vektor B.

       Ide yang paling penting dalam metode analitis ini adalah bahwa sebuah vektor selalu dapat diurai ke dalam dua komponen yang saling tegak lurus, dimana jika kita jumlahkan kedua komponen tersebut secara vektor, akan menghasilkan vektor semula! Selain dapat dinyatakan dengan menggunakan gambar anak panah, vektor juga dapat dinyatakan secara tertulis. Hal ini akan kita jumpai pada bahasan materi gerak, gaya ataupun tentang listrik dan magnet. Untuk menuliskan sebuah vektor, kita akan menggunakan bantuan sistem koordinat Cartesius (x, y dan z apabila kita memiliki vektor dalam suatu ruang 3 dimensi).
        Kini, sebuah vektor kembali dapat kita uraikan ke dalam komponen-komponen yang terletak pada masing-masing arah sumbu x, y dan z tersebut. Untuk menyatakan arah dalam sumbu-sumbu tadi, maka komponen suatu vektor diberi sebuah “vektor satuan”, i, j, dan k, yang merupakan sebuah vektor yang bernilai 1 satuan dalam arah sumbu x, y dan z.
        Misal, vektor A = A_xi + A_yj + A_zk, maka dapat dibayangkan vektor ini memiliki komponen Ax pada sumbu x, Ay pada sumbu y dan Az pada sumbu z.
        Untuk lebih jauh lagi mengenai penjumlahan vektor, silakan melihat Video Galileo To Einstein:

       Tentu selain operasi penjumlahan dan pengurangan pada vektor, masih terdapat operasi perkalian, dimana terdapat dua macam perkalian vektor yakni yang dinamakan perkalian titik (DOT) dan perkalian silang (CROSS). Kita tidak membahas kedua hal tersebut pada saat ini namun kita akan mendiskusikan kedua hal itu ketika kita memerlukannya nanti di pokok-pokok bahasan mendatang.

Gerak

Gambar  Sekelompok anak berlari dari rumah mereka menuju ke lapangan untuk bermain bola, mereka bergerak terhadap benda-benda yang ada di sekelilingnya, demikian juga sebaliknya.

       Semua benda di alam semesta ini bergerak! Mungkin ketika kita membaca pernyataan tadi, kita akan bertanya dan heran mengapa demikian, sebab kenyataan yang kita lihat dan alami sehari-hari, ada benda yang diam (terhadap kita)! seperti mobil yang sedang parkir, buku di meja, batu di taman dan sebagainya.
       Banyak hal yang ada di sekitar kita terkadang membuat kita sulit menerima konsep dasar yang ada dalam Fisika. Di materi-materi selanjutnya, kita akan melihat hal sehari-hari yang lain yang membuat kita sulit memahami konsep dasar fisika seperti Gaya dan pengaruhnya, Usaha dan energi. Kesalahpahaman yang terjadi akibat perbedaan hal yang kita pahami terhadap konsep yang benar dinamakan sebagai MISKONSEPSI dan hal tersebut adalah wajar sebagai salah satu langkah awal kita dalam belajar sesuatu! Justru mungkin ketika kita berangkat dari suatu miskonsepsi ketika mempelajari sesuatu, maka seringkali hal itu akan lebih membuat kita mengerti kebenaran akan hal tadi. 
       Setiap hari kita melihat benda-benda di sekitar kita bergerak terhadap kita. Burung terbang di udara, ikan berenang di sungai, anak-anak kecil berlari-larian, kereta melaju di atas rel dan masih banyak lagi. Mengapa suatu benda dikatakan bergerak? Sebuah benda kita katakan bergerak terhadap benda yang lain/acuan (referensi) apabila mereka mengalami perubahan tempat/posisi terhadap acuan tersebut.
       Menurut lintasan geraknya, gerak dapat dibagi ke dalam:
1. gerak 1 dimensi/arah (contoh : gerak lurus beraturan dan gerak lurus berubah beraturan)

Gambar  Kereta cepat Shinkansen di Jepang yang sedang bergerak lurus.

2.  gerak lebih dari 1 arah (2 dimensi, contoh : gerak parabola, gerak melingkar dan gerak dalam ruang 3 dimensi)

Gambar  : Gerak parabola sebagai contoh gerak dalam 2 arah

Sekarang mari kita diskusikan besaran-besaran penting yang dimiliki oleh benda yang bergerak:
1. Perpindahan : perubahan posisi benda.
2. Kecepatan    : perpindahan dibagi selang waktu tertentu.
3. Percepatan   : perubahan kecepatan benda dibagi selang waktu tertentu.
Ketiga besaran di atas memiliki dua informasi yang penting, yaitu nilai dan arah, sehingga kita golongkan mereka sebagai vektor!
       Benda yang bergerak dengan kecepatan 10 m/s artinya setiap detik, perpindahan yang dilakukan oleh benda tersebut sejauh 10 m pada arah tertentu.
Ada seorang berlari di sebuah lintasan yang lurus dari A ke B kemudian berbalik arah dan berhenti di C.

Seandainya titik A dan titik B berjarak 10 meter dan titik C berjarak 5 meter dari A. Tentukanlah jarak dan perpindahan dari gerak pelari tersebut !
Pertama, kita dapat menempatkan sebuah garis (sumbu) gerak sebagai berikut:

Mari kita beri nama sumbu ini sebagai sumbu x. Kita namai titik A sebagai titik x = 0, titik B adalah titik x = 10, dan titik C adalah titik x = 5. Kemudian titik-titik yang lain sebagai x = 1, x = 2, x = 3 dan seterusnya, dimana jarak antara satu titik ke titik berikutnya adalah sejauh 1 meter.

Tujuan dari pembuatan sumbu gerak dengan ukuran panjang pada sumbu tersebut adalah untuk mempermudah kita dalam melihat jarak dan perpindahan dari gerak orang tersebut.

Dari gambar di atas, dapat kita lihat bahwa orang itu bergerak dari A ke B sejauh 10 meter lalu berbalik arah sejauh 5 meter dan berhenti di C, maka jarak yang ditempuhnya adalah sejauh 15 meter. Jadi jarak merupakan panjang total dari lintasan yang ditempuh oleh benda. Sementara itu, perpindahan orang tersebut dapat kita gambarkan menggunakan sebuah panah yang berasal dari tempat awal (A)dan berakhir di tempat akhir (C).

Dari gambar panah tersebut, dapat dilihat bahwa orang berpindah ke arah kanan sejauh 5 meter. Perlu diperhatikan bahwa jarak tidak memiliki arah, namun perpindahan memiliki arah!
       Kini kita akan melihat kasus kedua tentang perpindahan. Jeslo berjalan 3 meter ke arah Utara, kemudian berbelok ke arah Timur sejauh 4 meter. Berapakah jarak dan perpindahan yang dilakukan oleh Jeslo ? Arah mata angin adalah sebagai berikut :

Perpindahan yang dilakukan oleh Jeslo adalah sebagai berikut:

Dapat kita lihat jarak yang ditempuh oleh Jeslo sejauh 7 meter dan perpindahannya sebesar 5 meter.
Sekarang kita  belajar beberapa konsep dasar yang akan sering kita jumpai dalam mempelajari gerak.
2.B.1 Kecepatan Rata-Rata dan Kecepatan Sesaat
       Ada satu konsep dasar umum yang perlu kita kenal, yakni yang dinamakan LAJU PERUBAHAN RATA-RATA (average rate of change), selanjutnya kita sebut sebagai laju perubahan. Secara matematika, laju perubahan besaran A ditulis sebagai Delta A/Delta waktu,  dimana DELTA menunjukkan perubahan nilai, nilai akhir dikurangi nilai awal. Suatu besaran yang mengalami perubahan (posisi, panjang, dan sebagainya) memiliki laju perubahan. 

       Laju perubahan suatu besaran mengandung pengertian sebagai perubahan besaran tersebut terhadap waktu (dibagi dengan suatu selang waktu tertentu). Misalkan, mula-mula terdapat sebuah wadah yang memuat 100 liter air, jika wadah tersebut bocor sehingga mengakibatkan seluruh air keluar dari wadah itu dalam waktu 20 menit. Maka laju perubahan volume air dalam wadah tersebut dari keadaan mula-mula hingga wadah kosong adalah -100 liter/20 menit (-5 liter/menit).
       Hal yang sama juga dapat kita terapkan pada gerak. Benda yang bergerak/berpindah tempat memiliki laju perubahan posisi benda atau dinamakan kecepatan rata-rata, yakni ukuran yang menyatakan perubahan posisi benda (perpindahan) dibagi dengan suatu selang waktu. Hati-hati, laju perubahan HENDAKNYA tidak dibingungkan dengan istilah kelajuan rata-rata yang akan kita jumpai nanti sebagai jarak tempuh dibagi waktu.
       Kecepatan dapat bernilai positif dan negatif, bergantung kepada arah gerak benda. Dapat kita sepakati bahwa untuk benda yang bergerak ke kanan maka nilai kecepatannya adalah positif dan sebaliknya. Secara fisik, kecepatan yang kita rasakan dalam pengalaman sehari-hari merupakan kecepatan sesaat, yang besarnya dapat diukur dengan alat ukur speedometer.

Gambar  Speedometer, alat untuk mengukur besar kecepatan.

  

2.B.2 Percepatan Dalam Fisika
       Percepatan merupakan suatu konsep yang abstrak dalam fisika. Meskipun kita memiliki definisi yang jelas tentang percepatan, yakni sebagai perubahan kecepatan dibagi selang waktu. Namun, tetap saja bagi banyak murid, hal tersebut masih sulit dimengerti.  Malah ada sebagian murid yang tidak dapat membedakan antara percepatan dan kecepatan.
       Kesulitan dalam memahami percepatan ini timbul sebagai akibat sulitnya membayangkan tentang hal tersebut dalam pengalaman sehari-hari. Deskripsi yang sering kali diberikan adalah jika benda mula-mula diam, lalu bergerak, maka benda memiliki percepatan. Penjelasan demikian memang sudah cukup baik, namun belum lengkap. Banyak aspek yang ada dalam percepatan. Benda yang berbelokpun juga memiliki percepatan meskipun besar dari kecepatan benda tersebut tidak berubah
       Hal kedua adalah bagi murid yang tidak memiliki dasar matematika yang kuat. Pemahaman kecepatan sebagai perubahan kecepatan masih agak membingungkan, dimana kecepatan sendiri merupakan sebuah besaran yang adalah hasil dari suatu perubahan. Ini seperti perubahan di dalam suatu perubahan.
       Salah satu pendekatan yang mudah dan dapat dicoba saat awal menjelaskan tentang percepatan adalah dimulai dari satuan percepatan itu sendiri, misalkan m/s². Satuan ini dapat dituliskan juga sebagai (m/s)/s. Dimana menyatakan suatu perhitungan pada kecepatan benda dibagi dengan waktu. Namun kemudian dijelaskan bahwa ini adalah suatu pendekatan awal yang sederhana untuk memahami percepatan.
       Pendekatan kedua yang dapat dicoba adalah dengan menjelaskan perbedaan antara kecepatan dan percepatan itu sendiri menggunakan bahasa. Dalam bahasa Inggris, terdapat dua kata yang jelas untuk membedakan keduanya, yakni kata fast untuk menggambarkan kecepatan dan kata quick untuk menggambarkan percepatan. Mungkin, kedua kata tadi dapat kita terjemahkan sebagai cepat dan gesit/sigap. Pesawat yang bergerak dengan kecepatan tinggi, belum tentu gesit. Seekor burung yang gesit, belum tentu bergerak dengan kecepatan yang tinggi (relatif).
       Tanpa bermaksud merendahkan Bahasa Indonesia, sayangnya banyak istilah-istilah Fisika yang menggunakan Bahasa Inggris memang terasa lebih tepat. Jadi, ada baiknya ketika kita mempelajari Fisika, kita juga sudah mulai diperkenalkan terhadap istilah berbahasa Inggris. Tentu hal tersebut bukan untuk alasan agar terdengar lebih hebat, namun, lebih karena makna yang terdapat di dalamnya. Hal-hal ini adalah hanya untuk membantu membedakan antara kedua hal tadi yakni kecepatan dan percepatan. Tentu ini semua belum sempurna, namun segala usaha untuk membuat siswa memahami makna dari percepatan dan dapat membedakan dengan kecepatan perlu kita upayakan.
       Secara matematika, kecepatan dan percepatan sangatlah berhubungan erat. Untuk melihat penjelasan yang lebih detail, silakan melihat Playlist Video Kelas Fisika Pak Ade materi ke-2 mengenai:
1. Percepatan rata-rata
2. Percepatan sesaat

2.B.3 Antara Posisi, Kecepatan dan Percepatan
       Dalam video-video tentang kecepatan dan percepatan di Sub Bab sebelumnya, kita belajar bagaimana dari posisi benda, kita bisa mendapatkan kecepatan dan percepatan benda tersebut. Kini, apabila kepada kita diberikan percepatan gerak benda, maka sekarang kita akan mencoba mendapatkan besaran yang sebaliknya yakni kecepatan dan posisi benda tersebut.
       Ide yang perlu dimengerti di bagian ini sebenarnya adalah, pertama, bahwa antara posisi, kecepatan dan percepatan sangatlah berkaitan erat dan secara matematis dapat dicari menggunakan kalkulus diferensial dan integral.

Kedua, konsep dasar yang penting dan setidaknya harus dipahami dengan benar adalah mengenai kecepatan rata-rata dan percepatan rata-rata.
 Gerak Satu Dimensi (pada sebuah sumbu)
       Gerak satu dimensi merupakan gerak yang paling mendasar dalam Fisika, dimana benda bergerak hanya pada suatu garis/sumbu. Gerak satu dimensi ini dapat membantu kita melihat perbedaan antara perpindahan dan jarak, serta antara kelajuan dan kecepatan karena hal-hal tersebut penting untuk dipahami dalam materi gerak.
       Pada kasus dimana benda hanya bergerak ke satu arah saja (tanpa berbalik arah), maka besar perpindahan benda dengan jarak yang ditempuh benda adalah sama, namun harus dipahami bahwa besar suatu perpindahan tidaklah selalu sama dengan jarak yang ditempuh benda sebab hal tersebut bergantung kepada lintasan yang ditempuh oleh benda, hanya pada gerak ke satu arah tertentu saja yang menghasilkan besar perpindahan sama dengan jarak. Demikian juga dengan besar kecepatan dan kelajuan benda, pada gerak ke satu arah, keduanya sama. Namun sekali lagi, ini hanya terjadi pada benda yang bergerak ke satu arah tertentu saja.
       Dalam materi gerak satu dimensi, pertama kita akan mempertajam pemahaman kita tentang jarak dan kelajuan rata-rata, lalu kita akan belajar tentang gerak yang umum dipelajari di SMA, yakni gerak lurus beraturan (GLB), gerak lurus berubah beraturan (GLBB) dan gerak jatuh bebas (GJB), dimana pada dua gerak terakhir tersebut, benda memiliki percepatan yang bernilai tetap, sehingga kecepatan benda akan mengalami perubahan secara teratur, dimana secara umum memiliki bentuk matematis, v = v₀ + a.t
       Meskipun demikian, ada gerak lurus yang percepatannya tidaklah tetap, namun mengalami perubahan saat benda tersebut bergerak. Ada yang menyebut gerak ini sebagai gerak lurus berubah tidak beraturan atau semacam itu, intinya, percepatan memiliki fungsi waktu, apapun itu bentuknya. Biasanya gerak semacam ini hanya dipelajari untuk sekadar berlatih pemahaman hubungan antara posisi, kecepatan dan percepatan sebagai fungsi waktu.
       Ketika belajar gerak, maka menyatakan/menggambarkan gerak benda ke dalam bentuk grafik terhadap waktu merupakan hal yang perlu dilatih, sebab grafik-grafik tersebut cukup sering membantu kita dalam menyelesaikan soal-soal gerak. Kedua, dengan grafik, kita juga dapat mencari beberapa informasi lain yang terkait didalamnya. Sebagai contoh adalah grafik kecepatan terhadap waktu. Ada suatu hal yang dapat diperhitungkan secara sederhana dengan menggunakan grafik kecepatan terhadap waktu, yaitu perpindahan (juga jarak) yang ditempuh benda dan percepatan benda.
       Sekarang perhatikan contoh sederhana ini. Sebuah benda bergerak dengan kecepatan yang tetap 5 m/s.
Perhatikan bagaimana jarak yang ditempuh oleh benda dari waktu ke waktu, pada detik pertama, jarak yang telah ditempuh adalah sejauh 5 m, pada detik kedua jarak yang telah ditempuh sejauh 10 meter dan seterusnya. 
Kita kemudian dapat membuat sebuah grafik yang menghubungkan antara jarak yang ditempuh terhadap waktu.
Ada suatu hubungan yang menarik antara grafik kecepatan terhadap waktu dengan jarak yang ditempuh oleh benda tersebut, dapatkah kamu melihat hal tersebut?
Apabila kita menghitung luas daerah yang berada di bawah grafik kecepatan terhadap waktu maka nilainya adalah sama dengan nilai jarak yang ditempuh tiap waktu.


2. Gerak dengan Kecepatan Tetap (Gerak Lurus Beraturan)
       Benda yang bergerak lurus beraturan memiliki kecepatan yang tetap setiap saat. Jadi, besar dan arah kecepatan benda selalu sama kapanpun (meskipun dalam pengalaman sehari-hari, hal tersebut sangat jarang terjadi pada benda yang bergerak).  Dikarenakan kecepatan yang tetap/tidak berubah, maka perubahan kecepatan bernilai nol, sehingga percepatan pada gerak lurus beraturan juga bernilai nol. Benda yang bergerak lurus beraturan akan menempuh jarak yang sama setiap satuan waktu gerak benda.
       Gambar di bawah memperlihatkan mobil yang bergerak dengan kecepatan yang tetap, kecepatan yang dipercepat secara teratur dan kecepatan yang diperlambat secara teratur.

Gambar  Perbedaan jarak tempuh benda yang (a) bergerak lurus beraturan, (b) bergerak dipercepat dan (c) bergerak diperlambat.

       Jika kita melakukan percobaan dengan memasang perekam gerak berupa ticker timer, maka rekaman titik-titik posisi benda akan sama jaraknya pada pita ticker timer tersebut.

Gambar  Rekaman pita ticker timer pada benda yang bergerak lurus beraturan

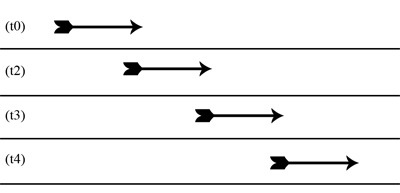
       Salah satu cara yang mudah dalam memahami gerak lurus beraturan adalah dengan mengerti makna dari besar kecepatan benda. Misalkan, benda bergerak dengan kecepatan 5 m/s artinya adalah dalam 1 detik, ia akan berpindah sejauh 5 meter.

Semakin besar kecepatan benda tersebut maka perpindahan yang dilakukannya akan menjadi semakin besar. Pada benda yang bergerak dengan kecepatan 10 m/s maka setiap detiknya benda menempuh jarak 10 meter.

Apabila kita menggambarkan grafik posisi terhadap waktu, maka kita akan melihat bahwa pada gerak lurus beraturan, grafik tersebut berupa sebuah garis miring.

Gambar 2.9 Grafik posisi terhadap waktu dari benda yang bergerak lurus beraturan.

Maka kecepatan, posisi akhir, posisi awal dan waktu dapat dituliskan sebagai:
Dapat kita lihat bahwa fungsi posisi terhadap waktu dari benda yang bergerak lurus beraturan mempunyai bentuk matematis sebagai fungsi linear/garis. Tentu pengetahuan fungsi gerak benda (posisi, kecepatan dan percepatan) terhadap waktu bukan suatu hal yang mutlak harus dikuasai pada saat mulai belajar tentang gerak. Ada begitu banyak cara yang cerdas dalam menyelesaikan sebuah soal gerak, di sinilah kita diajarkan tentang pentingnya berlatih banyak soal dan melihat penyelesaian yang paling mudah dan dapat dimengerti.

2. Gerak dengan Percepatan Tetap (Gerak Lurus Berubah Beraturan)
       Kecepatan dapat mengalami perubahan oleh karena dua hal, yakni berubah nilainya dan berubah arahnya. Dalam kedua hal tadi, maka benda memiliki percepatan!

Gambar  Gerak yang memiliki percepatan/perlambatan.

Dalam bagian ini kita akan memfokuskan pada benda yang memiliki percepatan sebagai akibat perubahan dari besar kecepatan benda. Ada sebuah mobil bergerak mula-mula dari keadaan diam, artinya kecepatan awal mobil tersebut adalah 0 m/s. Lalu 1 detik berikutnya berubah menjadi 2 m/s dan 1 detik kemudian berubah menjadi 4 m/s lalu menjadi 6 m/s, 8 m/s, 10 m/s dan seterusnya.
Dapatkah kamu menggambarkan grafik kecepatan mobil tersebut terhadap waktu?
Untuk benda yang bergerak dipercepat secara teratur/GLBB, kecepatan benda berubah dengan besar perubahan kecepatan selalu sama setiap detiknya sehingga penambahan/pengurangan kecepatan selalu sama. Jika kita gunakan ticker timer untuk menandai posisi benda ketika bergerak, maka pada benda yang dipercepat, jarak antara satu titik dengan titik berikutnya akan bertambah jauh sedangkan pada benda yang diperlambat, jarak antar titik akan semakin bertambah dekat.

Gambar  Benda yang bergerak lurus dipercepat beraturan.

Gambar  Benda yang bergerak lurus diperlambat beraturan.

Sekarang kita akan melihat perbedaan jarak tempuh pada benda yang bergerak dengan kecepatan tetap/GLB dengan  benda yang begerak lurus berubah beraturan/GLBB.
       Untuk dapat menghitung jarak yang ditempuh oleh benda yang bergerak secara GLBB, kita dapat membayangkan sebuah mobil yang dipercepat secara teratur, misalnya dari 5 m/s menjadi 6 m/s. Dalam 1 detik benda tersebut bergerak, maka jaraknya adalah nilai tengah dari jarak-jarak yang ditempuh oleh benda dengan 5 m/s dan benda dengan 6 m/s, yakni 5.5 meter.
Kini kita coba pikirkan lebih jauh dengan benda tadi dipercepat hingga mencapai 9 m/s maka jarak-jarak yang ditempuh setiap interval 1 detik akan seperti gambar berikut:
Selajutnya kita dapat menggambar grafik kelajuan/kecepatan  dan juga grafik jarak terhadap waktu

       Perhatikan bahwa grafik kelajuan/kecepatan terhadap waktu pada benda yang bergerak lurus berubah beraturan akan berupa sebuah garis miring, sedangkan grafik jarak  terhadap waktu akan membentuk suatu parabola.
Dengan menggunakan grafik kecepatan terhadap waktu,kita juga dapat mencari nilai percepatan gerak benda. Percepatan benda tersebut dapat dihitung sebagai gradien/kemiringan dari garis tersebut yakni perubahan kecepatan (v – v₀) dibagi interval waktu (t).
Sehingga
Lalu, jarak yang ditempuh dapat dihitung dengan menggunakan luas di bawah grafik kecepatan terhadap waktu.
Dengan menggunakan v = v₀ + a.t maka :
Dari rumus jarak tersebut, maka kita bisa mendapatkan fungsi posisi dengan cara mengganti jarak sebagai perpindahan (perubahan posisi = posisi akhir-posisi awal). Sehingga secara umum, fungsi posisi untuk benda yang bergerak berubah beraturan juga dapat ditulis:


Latihan soal GLB dan GLBB:
1. Ada anak berjalan menurut grafik posisi terhadap waktu seperti gambar. Tentukan kelajuan rata-rata dan kecepatan rata-rata anak itu dari t = 0 s hingga t = 6 s!

2. Seorang anak berjalan dengan grafik kecepatan terhadap waktu seperti pada gambar. berapakah kelajuan rata-ratanya dan kecepatan rata-ratanya?
3. Sebuah mobil dari keadaan diam dipercepat seperti pada gambar hingga bergerak selama 5 detik. Berapakah jarak yg ditempuh dan kecepatan pada detik ke-5 tersebut?
4. Ada mobil bergerak menurut garis lurus dari A ke B dan kembali ke A lagi, jika ketika bergerak dari A ke B kelajuannya 30 km/jam, dan ketika bergerak kembali dari B ke A kelajuannya 60 km/jam, berapakah kelajuan rata2nya dan kecepatan rata2nya ?
5. Duah buah mobil mula-mula berjarak 1000 meter, kemudian bergerak saling menuju. Kelajuan mobil pertama 3 m/s, kelajuan mobil kedua 2 m/s. Apabila saat mobil mulai bergerak, seekor lebah bergerak bolak-balik antara dua mobil itu dengan. Kelajuan 5 m/s. Hitunglah jarak total yang ditempuh oleh lebah sampai dengan kedua mobil bertemu!
6. Seorang agen rahasia berdiri di atas jembatan pada posisi 3/8 panjang jembatan tersebut (3/8 d). Saat agen tsb melihat mobil yang melaju dengan kelajuan yang tetap V, maka agen tersebut berlari dengan kelajuan yang tetap 10 m/s. Namun sungguh malang, ia akan tertabrak mobil di A jika ia berlari ke kiri dan ia akan tertabrak di B jika ia berlari ke kanan. Berapakah kelajuan mobil tersebut (V)?

7. Dua buah mobil A dan B bergerak dengan kecepatan konstan sepanjang garis PQ sepanjang 2000 meter. A bergerak dari P dengan kecepatan 20 m/s dan berangkat 5 detik lebih awal dari B. B bergerak dari P juga dengan kecepatan tetap 30 m/s. Dimanakah B akan menyusul A dan dimanakah B akan berpapasan dengan A setelah kembali dari Q!
8. Sebuah mobil bergerak dengan kecepatan 54 km/jam. Tiba-tiba mobil di rem dan berhenti setelah 2 detik. Hitunglah jarak yang ditempuh mobil tersebut selama pengereman!
9. Sebuah mobil bergerak dengan kecepatan 25 m/s. Setelah menempuh jarak 500 m, kecepatannya menjadi 10 m/s. Hitunglah perlambatan mobil tersebut!
10. Dua mobil bergerak saling menuju. A mula-mula bergerak dengan kecepatan awal 10 m/s, dipercepat dengan percepatan 5 m/s². B mula-mula bergerak dengan kecepatan awal 20 m/s dan dipercepat 10 m/s². Jarak mula-mula antara A dan B adalah 1000 m. Dimanakah mereka bertemu jika A berangkat 5 detik lebih awal dari B?
11. Sebuah benda bergerak dari keadaan diam dan dipercepat 3 m/s² lalu diperlambat dengan perlambatan sebesar 2 m/s² hingga berhenti. Jika total waktu yang diperlukan untuk gerak tersebut adalah 30 detik. Hitunglah jarak yang ditempuh benda tersebut !
12. Sebuah motor A dan mobil B bergerak dengan grafik kecepatan terhadap waktu seperti pada gambar.
– Hitunglah percepatan motor selama 0.2 jam pertama!
– Berapakah jarak yang ditempuh motor selama 0.3 jam pertama!
– Pada saat kapankah mobil akan bertemu dengan motor!
13. Andy dapat menempuh jarak rumah ke pasar dalam waktu 16 menit, Budi dapat menempuh jarak dari pasar ke rumah dalam waktu 24 menit. Anggap lintasan antara rumah dengan pasar adalah sebuah garis lurus, juga Andy dan Budi bergerak dengan kelajuan tetap. Jika Andy berangkat dari rumah pada menuju pasar pukul 07.00 sedangkan Budi berangkat dari pasar menuju rumah pada waktu 07.02, mereka pada suatu waktu akan bertemu di sebuah tempat pada lintasan tersebut. Apabila saat mereka bertemu,  selisih antara jarak yang telah ditempuh oleh Andy dengan jarak yang telah ditempuh oleh Budi adalah sejauh 200 meter. Berapakah jarak antara rumah dan pasar ?
14. Benda bergerak dipercepat beraturan. Anggap pada saat mula-mula benda dalam keadaan diam, sehingga kelajuan awalnya adalah 0 m/s. Jika setiap detik kecepatan benda bertambah 10 m/s.
a. Hitunglah jarak yang ditempuh
– dari t = 0 s ke t = 1 s,
– dari t = 0 s ke t = 2 s,
– dari t = 0 s ke t = 3 s,
b. Gambarkan grafik jarak yang ditempuh terhadap waktu !
15. Perhatikan grafik kecepatan terhadap waktu di bawah ini, sebuah mobil bergerak pada suatu arah tertentu (sebut saja arah x). Dapatkah kamu menceritakan bagaimana gerak mobil tersebut ?
15. Usain Bolt, pelari 100 m, memecahkan rekor dunia dengan catatan waktu 9,58 detik. Bagaimana kelajuan lari Usain Bolt dapat kita lihat pada gambar 11. Diskusikanlah bagaimana gerak dari Usain Bolt menggunakan gambar di bawah ini !
16. Kendaraan A dan B bergerak dari tempat yang sama pada sebuah lintasan lurus, dengan grafik kecepatan seperti pada gambar. Kapankah mereka memiliki kecepatan yang sama? berapakah selisih jarak antara mereka pada saat tersebut?
 2. Gerak Jatuh Bebas

Gambar 2.13 Galileo menjatuhkan dua benda yang berbeda massa dari balkon menara miring Pisa.

       Menurut legenda, Galileo pernah melakukan percobaan menjatuhkan dua benda yang berbeda beratnya. Menurut keyakinan orang-orang pada saat itu, benda yang lebih berat akan jatuh lebih cepat ketimbang benda yang ringan.
Galileo memperlihatkan bahwa mereka jatuh dalam waktu yang hampir bersamaan. Kedua benda yang jatuh bebas ditarik oleh gravitasi bumi sehingga pada geraknya terdapat percepatan  yang nilainya sebesar 9.8 m/s²≈ 10 m/s², artinya kecepatan benda mengalami perubahan sebesar 10 m/s setiap detiknya.
Secara umum, hubungan antara kecepatan, percepatan gravitasi dan waktu gerak benda dapat dituliskan sebagai berikut:
Lalu antara posisi akhir benda, posisi awal benda, kecepatan mula-mula, dan percepatan gravitasi dapat ditulis sebagai berikut:
dimana biasanya untuk mempermudah perhitungan, maka nilai g yang kita gunakan adalah 10 m/s². Fungsi kecepatan dan posisi tersebut berlaku secara umum, baik pada saat benda bergerak ke atas ataupun bergerak turun ke bawah. Kita tidak perlu membedakan tanda positif atau negatif untuk g pada keduanya.
Latihan soal Gerak Jatuh Bebas:

1. Apabila dianggap tidak ada gesekan udara, bola yang dilempar vertikal dari tanah akan sampai ke titik tertingginya dalam waktu yang sama ketika bola tersebut turun kembali sampai ke tanah. Nah, sekarang anggap ada suatu gaya gesek dan nilainya tetap, menurutmu, manakah yang lebih cepat, saat bergerak naik atau saat bergerak turun?

2. Soal ini dapat digunakan di sekolah bersama teman-teman untuk eksperimen mencari nilai percepatan gravitasi. Hanya diperlukan 3 orang/grup dan gedung sekolahnya yang setidaknya memiliki 3 lantai.
Seorang anak melempar bola (hijau) dari atas tanah, lalu Timer 1 dan Timer 2 mencatat waktu menggunakan stopwatch, mereka memulai pengukuran dan menghentikan pengukuran stopwatch saat bola tepat di depan pandangan mata mereka ketika bergerak naik dan turun.
Dimana waktu yg dicatat Timer 1 dan Timer 2 adalah t₁ dan t₂. Jika perbedaan ketinggian mereka adalah h (harus diukur terlebih dahulu!), maka nilai percepatan gravitasi adalah seperti pada gambar, g = (α.h)/t₁² – t₂², dimana alpha merupakan suatu bilangan. Berapakah nilai α? Setelah nilai α kita dapat, barulah kita dapat mencari nilai g dalam eksperimen tsb!

3. Sebuah benda dilempar vertikal dengan kecepatan awal 30 m/s, tentukan kelajuan rata-rata dan kecepatan rata-rata dari detik ke 2 sampai dengan detik ke 4? anggap tidak ada gesekan, hanya pengaruh gravitasi saja.
4. Sebuah benda dijatuhkan dari sebuah ketinggian, anggap ketika benda jatuh, ia mendapat gaya gesek yang besarnya sebanding dengan besar kecepatan benda, tentukan besar kecepatan benda terhadap waktu ! Berapakah kecepatan terminal benda ?
5. Pada tahun 1971, David Scott, seorang astronot menjatuhkan palu dan bulu di bulan. Ia menjatuhkan pada saat yang bersamaan. Manakah yang akan jatuh terlebih dahulu di permukaan bulan ?
A. Palu
B. Bulu
C. Bersamaan
Mengapa ?

6. Sebuah bola dijatuhkan dari suatu ketinggian tanpa kecepatan awal, dimana medium ruangan akan menghasilkan gaya gesek yang besarnya sebanding dengan kelajuan benda. Jika kita gambarkan grafik antara percepatan gerak terhadap waktu. Manakah grafik di bawah ini yang akan menggambarkan percepatan gerak benda tsb?

Manakah grafik yang menggambarkan kecepatan benda tersebut?

7. Sebuah roket meluncur dari tanah, dengan kecepatan awal 50 m/s, roket mendapat percepatan dari bahan bakar sebesar 5 m/s². Jika pada ketinggian 1000 meter bahan bakar roket habis. Hitunglah:

– Waktu ketika roket mencapai posisi tertinggi
– Posisi tertinggi roket tersebut
– Waktu tiba di tanah
– Besar kecepatan roket saat tiba di tanah!